1. Introduction
Scaled physical models are often used in science and engineering to approximate real-world systems. The principle of dynamic similarity allows for geometrically-scaled systems to be dynamically identical if certain nondimensional physical parameters are matched. In the case of fluid systems, the most important nondimensional parameter is often the Reynolds number,
, which quantifies the importance of inertial forces over viscous forces on the flow physics [
1]:
, where
U and
l are characteristic velocity and length scales, respectively, and
ν is the fluid kinematic viscosity. The other common dynamical scale, for systems with a free surface, is the Froude number
, where
g is the gravitational acceleration. Matching both the Froude and Reynolds number is not possible for a scaled model in a given fluid, which is illustrated by the relation
, since
scales linearly with
l, or the geometric scale. In general, the geometric scale of a physical model is not necessarily the same as its dynamical scale. As such, hereafter, we will use the word “scale” to refer to this dynamical scale or the Reynolds number and assume the Froude number is small enough to be negligible.
With regards to wind and marine hydrokinetic (MHK) turbines, scaled physical models are used to validate predictive numerical models, predict full-scale performance of individual turbines and design or investigate arrays of devices. Scaled models have the benefit of being significantly less expensive; however, a key question is whether or not an acceptable scale mismatch exists. Similarly, it is questionable whether numerical models validated with physical model data obtained orders of magnitude away from prototype scale should be considered validated at all. An example of the errors that can result from the extrapolation of small-scale experiments can be found in [
2].
The performance and wake characteristics of cross-flow (often vertical-axis) turbines (CFTs) depend on turbine solidity, blade profile (lift/drag, dynamic stall at reduced frequency of turbine rotation, symmetry, thickness, camber), blade pitch, number of blades, strut drag, operational parameters, such as tip speed ratio, and on the Reynolds number [
3]. Note that an average blade chord Reynolds number,
, can be expressed in terms of tip speed ratio
, where
is the free stream velocity,
c is the blade chord length,
ν is the fluid kinematic viscosity,
ω is the rotor’s angular velocity, and
R is the rotor radius. The value of
λ at which a turbine reaches peak performance in general decreases with turbine solidity
[
4], which allows for the use of a simpler Reynolds number based on turbine diameter
.
Solidity often directly correlates with the chord-to-radius ratio
. Rotors with
are considered to have high solidity [
5], for which so-called flow curvature or virtual camber effects become significant [
6]. These effects arise from the blade sections’ circular paths and can complicate the comparison with the behavior of an airfoil in a linear flow.
Blackwell
et al. [
7] investigated the effects of Reynolds number on the performance of a 2 m diameter Darrieus vertical-axis cross-flow wind turbine with NACA 0012 blades. By varying wind tunnel speed, the turbine was made to operate at an approximately constant blade chord Reynolds number
ranging from
to
. In this regime, the turbine power coefficient
was shown to be sensitive to
, with sensitivity diminishing at the higher Reynolds numbers, especially for turbines of lower solidity (
, where
N is the number of blades and
R is the turbine’s maximum radius). More recently, Polagye and Cavagnaro [
8] observed significant Reynolds number sensitivity for a high solidity helical cross-flow turbine, and Bravo
et al. [
9] observed the power coefficient of a straight-bladed vertical-axis wind turbine (VAWT) to become Reynolds number independent at
. Bachant and Wosnik [
10] observed Reynolds number independence of the power coefficient at the optimal tip speed ratio for a high solidity cross-flow turbine at
or
.
The wake of a 2D cross-flow turbine in the dynamic stall regime has been studied via laser Doppler velocimetry by Brochier
et al. [
11] and in 3D with particle image velocimetry (PIV) by Fujisawa and Shibuya [
12]. However, both of these studies were performed at very low Reynolds numbers:
and
, respectively. Tescione
et al. [
13] studied the wake of a vertical-axis wind turbine at its optimal tip speed ratio in a wind tunnel using stereo PIV at an approximate blade chord Reynolds number
; very close to the
-independence criteria reported in [
10], though it was not confirmed if this was indeed a
-independent state. The two lower
experiments tended to focus on the effects of dynamic stall, whereas the higher
experiment mostly concerned the mean velocity and tip vortex effects. Whereas the value of these studies was in elucidating the complex wake dynamics of cross-flow turbines, they also motivated the more systematic investigation of scale effects undertaken here.
Scale effects on axial-flow or horizontal-axis wind turbines are better understood, and investigators have methods for compensating. Krogstad and Adaramola [
14] observed Reynolds number independence of the performance of a 0.9 m diameter axial-flow turbine rotor at
in wind tunnel tests. Their turbine blades had an S826 profile along their entire span, a profile chosen for its
-independence. Walker
et al. [
15] similarly chose a NACA 63-618 foil for their axial-flow turbine tests in a towing tank, which were performed at a mid-span Reynolds number
. McTavish
et al. [
16] showed how the near-wake expansion for an axial-flow rotor is increased at higher Reynolds numbers, concluding that physical models should be designed with
-independence in mind if they are to be run at low
. It is uncertain, however, if these methods work equally well for cross-flow turbines.
When designing or studying arrays, it is common to use very small (geometrically) scaled devices [
17,
18]. It is therefore important to realize the limitations of evaluating both the power output of turbines and the wake recovery when the Reynolds number is very far from full scale. Sometimes, the models used are not turbines, but wake-generating objects, e.g., porous disks, that are meant to replicate the wakes of real turbines [
19]. In this case, it is of interest to determine at what Reynolds number one might be able to realistically study wake flows in an array and also to evaluate the effectiveness of a wake generator. In other words, a wake generator may do a fine job simulating a scaled turbine, but how well can it simulate a full-scale device? Note that for a porous disk, the Reynolds number of interest is based on diameter, since it is the scaling of the far-wake dynamics that matters.
Vertical-axis wind turbine array field experiments have revealed that improved wake recovery allows for closer spacing when compared to conventional axial-flow propeller-type turbines [
20,
21]. It was observed experimentally that a high solidity vertical-axis cross-flow turbine’s near-wake produces a unique vertical mean velocity field, generated by blade tip vortex shedding, the advection by which is the largest contributor to streamwise momentum and energy transport or recovery [
22]. In this study, we seek to replicate those same momentum and energy balance considerations at multiple Reynolds numbers, to examine the implications on how scaled,
i.e., low Reynolds number experiments, may be used to study flows in turbine arrays.
Modes of Reynolds Number Dependence
It is of interest to examine how Reynolds number scaling affects both the blade loading,
i.e., turbine performance, and the near-wake. Typically, static airfoil data show that the static stall angle increases with blade chord Reynolds number
[
23]. A review of Reynolds number effects on airfoil behavior is presented in [
24]. In general, airfoil performance, often characterized by the profile’s lift-to-drag ratio, is enhanced as the boundary layer on the foil transitions to turbulence closer to the leading edge, which enables it to advance further downstream against the adverse pressure gradient on the suction side, delaying separation to higher angles of attack. For smooth airfoils, this transition can cause a dramatic increase in foil performance at a blade chord Reynolds number on the order of
[
25]. Note that there is a distinct lack of highly reliable data for airfoils in this transitional regime and below. An evaluation of the various databases relevant to cross-flow turbines is presented in [
26].
Static foil performance does not tell the whole story for a cross-flow turbine. The azimuthal, and therefore, temporal, variation of
α in a cross-flow turbine implies dynamic loading, encountering dynamic stall for tip speed ratios near and below those of maximum rotor torque [
3]. Bousman [
27] states that dynamic stall is relatively insensitive to Reynolds number for
to
, judging from measurements on a pitching VR-7 foil in a wind and water tunnel, since the loading is dominated by vortex shedding. However, Singleton and Yeager Jr. [
28] state that the effect of Reynolds number on dynamic stall remains an unsolved question.
Despite lower lift on the blades at lower
, we expect stronger tip vortex shedding [
29]. As mentioned previously, the dynamic stall vortex shedding is not expected to be highly sensitive to Reynolds number, though a larger separation bubble at lower
may induce higher levels of turbulence as shed vortices become unstable and break down.
Chamorro
et al. [
30] showed that turbulence statistics in an horizontal-axis or axial-flow wind turbine wake became
-independent at
and that mean velocity profiles became
-independent slightly earlier at
. Note that in this study, the tip chord Reynolds number was not reported, but is estimated to be
at
. It is therefore our objective to observe similar scaling relationships for a cross-flow turbine near-wake.
2. Experimental Setup
Experiments were performed in a turbine test bed specifically designed for cross-flow turbines. The test bed was integrated as part of the University of New Hampshire (UNH) tow tank, which is a 36 m-long facility with a 3.66 m-wide and 2.44 m-deep cross-section. The turbine model used in this study was the UNH Reference Vertical Axis Turbine (RVAT), which was designed to be a generic case for numerical model testing, similar to the Sandia National Labs/U.S. Department of Energy Reference Model 2 (RM2) River Turbine [
31], but with a higher solidity or blade chord-to-radius ratio.
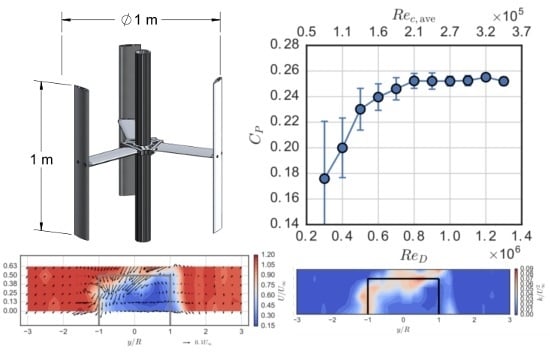
The UNH-RVAT turbine has three blades made from NACA 0020 profiles with a 0.14 m chord. The blades are mounted at mid-chord w.r.t. the turbine axis, and the turbine has a height (blade span) of 1 m and a diameter of 1 m;
cf.
Figure 1. The blockage ratio produced by the rotor’s frontal area is 11%, which we decided not to correct for, as reliable methods are not yet agreed upon for CFTs [
32]. As such, blockage should be taken into account when using these data for model validation,
i.e., the experimental domain should be mimicked. The rotor has a relatively high solidity
and a large chord-to-radius ratio
. A CAD model of the turbine is available from [
33].
Figure 1.
University of New Hampshire Reference Vertical Axis Turbine (UNH-RVAT) turbine model. Turbine blades and struts made from NACA 0020 profiles with 0.14 m chord. Note that the upper and lower mounting flanges have been excluded, as these were included in the tare drag measurements.
Figure 1.
University of New Hampshire Reference Vertical Axis Turbine (UNH-RVAT) turbine model. Turbine blades and struts made from NACA 0020 profiles with 0.14 m chord. Note that the upper and lower mounting flanges have been excluded, as these were included in the tare drag measurements.
The turbine was mounted in a frame constructed from NACA 0020 sections, shown in
Figure 2. The turbine shaft ran up through the water surface, coupled to a Kollmorgen AKM permanent magnet servo motor (Kollmorgen, Radford, VA, USA) with a 20:1 gearbox, providing precise control over shaft angular velocity. This servo was controlled by the tow tank’s main motion controller for high synchronization with the carriage motion, thereby giving precise measurement and control of the tip speed ratio. An Interface T8 200 Nm capacity rotary torque transducer (Interface, Scottsdale, AZ, USA) was installed inline between the servo and the turbine, and the servo was also mounted on a slewing ring bearing, which allowed a redundant measurement of torque via an arm and load cell used to counteract the turbine moment. The frame was mounted to the carriage via linear guides, such that the total streamwise drag force was transferred to a pair of Sentran ZB3 500 pound-force capacity S-beam load cells (Sentran, Santa Ana, CA, USA), providing the rotor drag measurements, after a separately measured tare drag was subtracted in post-processing. Similarly, a tare torque was measured by rotating the turbine shaft in air. Turbine angular and tow carriage linear position were measured using quadrature encoder signals, with
counts-per-rev for the turbine and 10
μm resolution for the carriage position. These signals, along with the torque and drag signals, were sampled at 2 kHz.
Wake velocity was measured using a Nortek Vectrino+ acoustic Doppler velocimeter (ADV) (Nortek AS, Rud, Norway), which has an approximately 6 mm diameter sampling volume and sampled at 200 Hz. The probe was mounted on an automated positioning system, also controlled by the tow tank’s main motion controller. The ADV and data acquisition systems’ sampling times were synchronized by triggering the start of data acquisition via a pulse sent from the motion controller. Additional details of the turbine and experimental setup are described in [
22].
Figure 2.
Experimental setup photo (a) and drawing (b): turbine test bed installed in the UNH tow tank.
Figure 2.
Experimental setup photo (a) and drawing (b): turbine test bed installed in the UNH tow tank.
2.1. Test Plan
Approximately 1500 tows were conducted for the study reported here; each tow was used for a single data point on either a performance curve or wake map. Each performance curve consisted of 31 tows, where during each tow, the mean turbine tip speed ratio was held constant, ranging from 0.1 to 3.1 in 0.1 increments. Full performance curve data were acquired for tow speeds from 0.4 to 1.2 m/s in 0.2 m/s increments, for which the turbine diameter and approximate blade chord Reynolds number are presented in
Table 1. Performance was also measured for
at tow speeds
m/s for two tows each.
Each wake map was generated by positioning the ADV, which measured three components of velocity at a 200 Hz sampling frequency, at 270 different locations, varied in the cross-stream and vertical directions at one turbine diameter downstream (
). These locations had vertical coordinates from the turbine centerline up to
, ranging in the cross-stream direction
. These locations are shown in
Figure 3.
Table 1.
Turbine diameter and approximate blade chord Reynolds numbers for the tow speeds used in the experiment.
Table 1.
Turbine diameter and approximate blade chord Reynolds numbers for the tow speeds used in the experiment.
| Tow Speed (m/s) | | () |
|---|
| 0.3 | | |
| 0.4 | | |
| 0.5 | | |
| 0.6 | | |
| 0.7 | | |
| 0.8 | | |
| 0.9 | | |
| 1.0 | | |
| 1.1 | | |
| 1.2 | | |
| 1.3 | | |
Figure 3.
Wake measurement coordinate system and locations. Dimensions are in meters.
Figure 3.
Wake measurement coordinate system and locations. Dimensions are in meters.
2.2. Data Processing
From each set of tows, a standard time interval was set, which allowed the turbine performance and wake to reach a quasi-periodic state. Each run was analyzed to compute statistics over this interval, truncating the end slightly to achieve an integer number of blade passages. Turbine shaft angular velocity and tow carriage speed were calculated using a second order central differencing scheme on the respective position measurements. Power and drag coefficients were calculated as instantaneous quantities using the carriage speed as the free stream velocity.
Wake velocity data were filtered for spurious “spikes” by removing data points 8 standard deviations, or 0.9 m/s, from the mean. The experimental data and code for processing and visualization are available from [
34].
2.3. Uncertainty Analysis
Uncertainty was considered from a combination of systematic and random errors. The random error was inferred from the sample standard deviation (on a per-revolution basis) and the systematic error from the sensor calibrations or datasheets. Combining both sources of error, along with their propagation into quantities derived from multiple measurements, followed the procedures outlined in Coleman and Steele [
35], described below.
An expanded uncertainty interval with 95% confidence was computed for
,
, and mean wake velocities:
where
is the value from the Student
t-distribution for a 95% confidence interval and
is the combined standard uncertainty. Combined standard uncertainty for a given quantity
X is calculated by:
where
is the sample standard deviation of the mean per turbine revolution, and
is the systematic uncertainty, computed by:
where
is a primitive quantity used to calculate
X (e.g.,
T,
ω, and
for calculating
), and
is the primitive quantity’s systematic uncertainty, estimated as half the value listed on the sensor manufacturer’s documentation.
Selecting
requires an estimate for degrees of freedom
, which was obtained using the Welch–Satterthwaite formula:
where
is the number of degrees of freedom associated with
and
is the number of degrees of freedom associated with
.
is assumed to be
, where
N is the number of independent samples (or turbine revolutions).
was estimated as:
where the quantity in parentheses is the relative uncertainty of
, assumed to be 0.25.
For the Reynolds number dependence of turbine performance, error bars are included on the plots. Expanded uncertainty estimates for mean wake velocities (averaged over all runs) are listed in
Table 2.
Table 2.
Average expanded uncertainty estimates (with 95% confidence) for mean velocity measurements at each tow speed.
Table 2.
Average expanded uncertainty estimates (with 95% confidence) for mean velocity measurements at each tow speed.
| (m/s) | U (m/s) | V (m/s) | W (m/s) |
|---|
| | | |
| | | |
| | | |
| | | |
| | | |
4. Conclusions
In this study, it was demonstrated that the performance of a high solidity (
) cross-flow turbine becomes essentially
-independent at a Reynolds number based on the turbine diameter
or an approximate Reynolds number based on the blade chord
. The power coefficient values on the left-hand side of the
-
λ curve are reduced more than those on the right-hand side at low
due to deeper stalling. The
-independent threshold corresponds to that at which the foil suction surface boundary layer becomes turbulent before having to recover static pressure against the adverse pressure gradient, highlighted in [
24,
25,
40].
We propose a method for predicting the Reynolds number dependence of a cross-flow turbine using static airfoil characteristics and turbine blade kinematics:
Acquire static lift and drag coefficient data for the desired blade profile.
For azimuthal angles of 0 to 180 degrees and a given tip speed ratio, calculate the geometric angle of attack and relative velocity magnitude from the blade and undisturbed free stream velocity (taken as unity) vectors.
With arrays of geometric angle of attack and relative velocity magnitude, calculate the blade chordwise force and then the rotor torque coefficient from Equations (
6) and (
7), respectively.
Extract the maximum value of , and repeat this process for static foil data at multiple .
It was shown that the peak torque coefficient computed this way shows similar Reynolds number sensitivity as the experimental results for an actual turbine, making it a better predictor than conventional quantifications of airfoil performance, e.g., the lift-to-drag ratio. Note that this method is not restricted to standard symmetrical NACA foils, though those evaluated here with higher camber were more sensitive at lower , but had smaller slopes in the linear regime.
In the near-wake of the turbine, we observed lower levels of turbulence with increasing Reynolds number, along with lower levels of turbulent transport with respect to mean streamwise momentum and mean kinetic energy recovery in the streamwise direction. Vertical advection, the largest transport mechanism measured, showed little -dependence, whereas the negative effects of cross-stream advection were enhanced at high , which may be due to larger free surface deformation effectively reducing the near-wake’s cross-sectional area. Despite being orders of magnitude smaller than other transport processes, viscous diffusion increased rapidly with decreasing and is expected to become significant to the wake dynamics around . Overall, the total wake transport measured leveled off at essentially the same Reynolds number that the performance did: .
From these results, we recommend that physical model tests of cross-flow turbines be performed at
or greater to provide reasonable predictions of full-scale performance. This threshold also applies to the validation of predictive engineering models, especially for high-fidelity CFD models where the boundary layer is to be resolved, since transition to turbulence plays an important role in overall blade loading. Note that in our case, blockage, though reasonably low, may be increasing flow through the turbine compared to a free case, which could mean
thresholds for free flows could be slightly higher, though a reliable blockage correction algorithm has not yet been agreed upon for CFTs [
32].
If using scaled physical models to predict array performance, where turbine power output is measured, it may also be important to keep all turbines in the regime where the power coefficient varies linearly to avoid exaggerated power deficiencies for downstream turbines, despite similarities in wake characteristics. Results here also suggest that low Reynolds number physical model studies of turbine arrays may see exaggerated levels of wake recovery, leading to inadequate or inappropriate spacing or layouts.