Numerical Study of Solidification in a Plate Heat Exchange Device with a Zigzag Configuration Containing Multiple Phase-Change-Materials
Abstract
:1. Introduction
2. Numerical Modelling
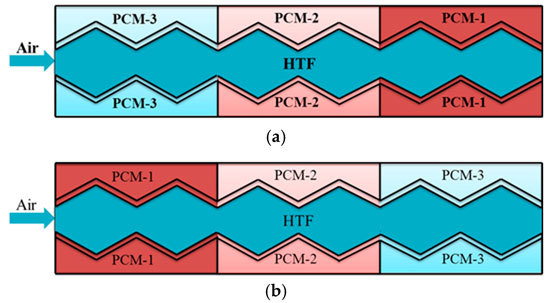
2.1. Physical Model
2.2. Governing Equation
2.3. Boundary Conditions
- Tin = T (constant or changed with time depending on the work condition);
- vin = v (constant or changed with time depending on the work condition);
- To = 803.15 K.
2.4. Numerical Modelling
3. Experimental Verification
3.1. Experimental System and Procedure
3.2. Verification and Validation of the Simulation Models
4. Modelling Results and Discussion
4.1. Multiple Phase-Change-Materials in Different Arrangements
4.2. Effect of Different Ste or Re Numbers
4.3. Effect of Different Ste/Re under a Given Inlet Power
5. Conclusions
- (1)
- It is more advantageous for the plate energy storage unit to arrange the m-PCMs in a reversed direction than in a forward direction.
- (2)
- If only the Ste (inlet temperature) or Re (inlet velocity) numbers were changed, there was almost no impact of the Ste number on the discharge process of the m-PCMs unit, but there was a significant impact of the Re number; for a given inlet power inlet condition, it was more advantageous to increase the Re number than the Ste number to shorten the phase change time in the discharge process.
- (3)
- For a given inlet power condition with a periodically varying velocity, the value of the period (30 s–10 min) had almost no impact on the discharge process, which indicates that the zigzag plate with m-PCMs had a positive impact on the temperature shock.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | Mushy zone constant |
| Aa | Cross-sectional area |
| cp | Specific heat, J/(kg·K) |
| h | Sensitive heat, J |
| H | Enthalpy, J |
| L | Latent heat of the material, J/kg |
| m | Mass, kg |
| P | Pressure/inlet power, Pa/W |
| QL | Latent heat, J |
| Qall | Total stored heat, J |
| Re | Reynolds number |
| Sb | Buoyancy source term |
| Sh | Energy source term |
| Si | Momentum sink in i direction |
| St | Turbulence source term |
| Ste | Stefan number |
| t | Time, s |
| T | Temperature, K |
| T | Period |
| To | Initial temperature, K |
| TPCM-1/2/3 | Phase change temperature of PCM-1/2/3, K |
| Velocity vector, m/s | |
| w | Width of the inlet, m |
Greek Symbols
| α | Thermal conductivity, W/(m·K) |
| β | Liquid fraction or porosity |
| ρ | Density, kg/m3 |
| μ | Viscosity, kg/(m·s) |
| ε | Amall number |
| τ | Dimensionless time |
| ΔT | Temperature difference between TPCM-1 and TPCM-3, K |
| ω | Mass fraction |
| Φ | Turbulence parameter |
Subscript
| ave | Average value |
| b | Base value or buoyancy |
| in | Inlet value |
| l/s | Liquid/solid phase |
| ref | Reference value |
| t | Turbulence or value in t moment |
References
- Pomianowski, M.; Heiselberg, P.; Zhang, Y. Review of thermal energy storage technologies based on PCM application in buildings. Energy Build. 2013, 67, 56–69. [Google Scholar] [CrossRef]
- El Qarnia, H.; Draoui, A.; Lakhal, E.K. Computation of melting with natural convection inside a rectangular enclosure heated by discrete protruding heat sources. Appl. Math. Model. 2013, 37, 3968–3981. [Google Scholar] [CrossRef]
- Kandasamy, R.; Wang, X.Q.; Mujumdar, A.S. Transient cooling of electronics using phase change material (PCM)-based heat sinks. Appl. Therm. Eng. 2008, 28, 1047–1057. [Google Scholar] [CrossRef]
- Nomura, T.; Oya, T.; Okinaka, N.; Akiyama, T. Feasibility of an advanced waste heat transportation system using high-temperature phase change material (PCM). ISIJ Int. 2010, 50, 1326–1332. [Google Scholar] [CrossRef]
- Shon, J.; Kim, H.; Lee, K. Improved heat storage rate for an automobile coolant waste heat recovery system using phase-change material in a fin-tube heat exchanger. Appl. Energy 2014, 113, 680–689. [Google Scholar] [CrossRef]
- Antony Aroul Raj, V.; Velraj, R. Heat transfer and pressure drop studies on a PCM-heat exchanger module for free cooling applications. Int. J. Therm. Sci. 2011, 50, 1573–1582. [Google Scholar] [CrossRef]
- Izquierdo-Barrientos, M.A.; Belmonte, J.F.; Rodríguez-Sánchez, D.; Molina, A.E.; Almendros-Ibáñez, J.A. A numerical study of external building walls containing phase change materials (PCM). Appl. Therm. Eng. 2012, 47, 73–85. [Google Scholar] [CrossRef]
- Parameshwaran, R.; Kalaiselvam, S. Energy conservative air conditioning system using silver nano-based PCM thermal storage for modern buildings. Energy Build. 2014, 69, 202–212. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, X.; Xu, G. Thermal performance of a solar storage packed bed using spherical capsules filled with PCM having different melting points. Energy Build. 2014, 68, 639–646. [Google Scholar] [CrossRef]
- Agyenim, F.; Hewitt, N. The development of a finned phase change material (PCM) storage system to take advantage of off-peak electricity tariff for improvement in cost of heat pump operation. Energy Build. 2010, 42, 1552–1560. [Google Scholar] [CrossRef]
- Qureshi, W.A.; Nair, N.K.C.; Farid, M.M. Impact of energy storage in buildings on electricity demand side management. Energy Convers. Manag. 2011, 52, 2110–2120. [Google Scholar] [CrossRef]
- Li, W.Q.; Qu, Z.G.; He, Y.L.; Tao, W.Q. Experimental and numerical studies on melting phase change heat transfer in open-cell metallic foams filled with paraffin. Appl. Therm. Eng. 2012, 37, 1–9. [Google Scholar] [CrossRef]
- Ge, Z.; Ye, F.; Cao, H.; Leng, G.; Qin, Y.; Ding, Y. Carbonate-salt-based composite materials for medium- and high-temperature thermal energy storage. Particuology 2014, 15, 77–81. [Google Scholar] [CrossRef]
- Gong, Z.X.; Mujumdar, A.S. Enhancement of energy charge-discharge rates in composite slabs of different phase change materials. Int. J. Heat Mass Transf. 1996, 39, 725–733. [Google Scholar] [CrossRef]
- Gong, Z.X.; Mujumdar, A.S. Cyclic heat transfer in a novel storage unit of multiple phase change materials. Appl. Therm. Eng. 1996, 16, 807–815. [Google Scholar] [CrossRef]
- Ismail, K.A.R.; Lino, F.A.M. Fins and turbulence promoters for heat transfer enhancement in latent heat storage systems. Exp. Therm. Fluid Sci. 2011, 35, 1010–1018. [Google Scholar] [CrossRef]
- Wang, Y.H.; Yang, Y.T. Three-dimensional transient cooling simulations of a portable electronic device using PCM (phase change materials) in multi-fin heat sink. Energy 2011, 36, 5214–5224. [Google Scholar] [CrossRef]
- Nithyanandam, K.; Pitchumani, R. Analysis and optimization of a latent thermal energy storage system with embedded heat pipes. Int. J. Heat Mass Transf. 2011, 54, 4596–4610. [Google Scholar] [CrossRef]
- Robak, C.W.; Bergman, T.L.; Faghri, A. Enhancement of latent heat energy storage using embedded heat pipes. Int. J. Heat Mass Transf. 2011, 54, 3476–3484. [Google Scholar] [CrossRef]
- Tao, Y.B.; He, Y.L.; Qu, Z.G. Numerical study on performance of molten salt phase change thermal energy storage system with enhanced tubes. Sol. Energy 2012, 86, 1155–1163. [Google Scholar] [CrossRef]
- Darzi, A.R.; Farhadi, M.; Sedighi, K. Numerical study of melting inside concentric and eccentric horizontal annulus. Appl. Math. Model. 2012, 36, 4080–4086. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Sasmito, A.P.; Jangam, S.V.; Mujumdar, A.S. Improved design for heat transfer performance of a novel phase change material (PCM) thermal energy storage (TES). Appl. Therm. Eng. 2013, 50, 896–907. [Google Scholar] [CrossRef]
- Seeniraj, R.V.; Narasimhan, N.L. Performance enhancement of a solar dynamic LHTS module having both fins and multiple PCMs. Sol. Energy 2008, 82, 535–542. [Google Scholar] [CrossRef]
- Ismail, K.; Alves, C.; Modesto, M. Numerical and experimental study on the solidification of PCM around a vertical axially finned isothermal cylinder. Appl. Therm. Eng. 2001, 21, 53–77. [Google Scholar] [CrossRef]
- Blen, K.; Takgil, F.; Kaygusuz, K. Thermal Energy Storage Behavior of CaCl2·6H2O during Melting and Solidification. Energy Sources 2008, 30, 775–787. [Google Scholar]
- Ismail, K.A.R.; Filho, L.M.S.; Lino, F.A.M. Solidification of PCM around a curved tube. Int. J. Heat Mass Transf. 2012, 55, 1823–1835. [Google Scholar] [CrossRef]
- Al-Abidi, A.A.; Mat, S.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Experimental study of melting and solidification of PCM in a triplex tube heat exchanger with fins. Energy Build. 2014, 68, 33–41. [Google Scholar] [CrossRef]
- Al-Abidi, A.A.; Mat, S.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Numerical study of PCM solidification in a triplex tube heat exchanger with internal and external fins. Int. J. Heat Mass Transf. 2013, 61, 684–695. [Google Scholar] [CrossRef]
- Mosaffa, A.H.; Infante Ferreira, C.A.; Talati, F.; Rosen, M.A. Thermal performance of a multiple PCM thermal storage unit for free cooling. Energy Convers. Manag. 2013, 67, 1–7. [Google Scholar] [CrossRef]
- Francesco, C.; Sciacovelli, A.; Verda, V. Numerical analysis of a medium scale latent energy storage unit for district heating systems. Energy 2012, 45, 397–406. [Google Scholar]
- Wang, P.; Wang, X.; Huang, Y.; Li, C.; Peng, Z.; Ding, Y. Thermal energy charging behaviour of a heat exchange device with a zigzag plate configuration containing multi-phase-change-materials (m-PCMs). Appl. Energy 2015, 142, 328–336. [Google Scholar] [CrossRef]
















| Density | Thermal Conductivity | Specific Heat | Melting Point | Latent Heat |
|---|---|---|---|---|
| kg/m3 | W/m·K | kJ/(kg·K) | K | kJ/kg |
| 2200 | 0.6 | 0.93 | 713.15 | 280 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Li, D.; Huang, Y.; Zheng, X.; Wang, Y.; Peng, Z.; Ding, Y. Numerical Study of Solidification in a Plate Heat Exchange Device with a Zigzag Configuration Containing Multiple Phase-Change-Materials. Energies 2016, 9, 394. https://doi.org/10.3390/en9060394
Wang P, Li D, Huang Y, Zheng X, Wang Y, Peng Z, Ding Y. Numerical Study of Solidification in a Plate Heat Exchange Device with a Zigzag Configuration Containing Multiple Phase-Change-Materials. Energies. 2016; 9(6):394. https://doi.org/10.3390/en9060394
Chicago/Turabian StyleWang, Peilun, Dacheng Li, Yun Huang, Xingang Zheng, Yi Wang, Zhijian Peng, and Yulong Ding. 2016. "Numerical Study of Solidification in a Plate Heat Exchange Device with a Zigzag Configuration Containing Multiple Phase-Change-Materials" Energies 9, no. 6: 394. https://doi.org/10.3390/en9060394
APA StyleWang, P., Li, D., Huang, Y., Zheng, X., Wang, Y., Peng, Z., & Ding, Y. (2016). Numerical Study of Solidification in a Plate Heat Exchange Device with a Zigzag Configuration Containing Multiple Phase-Change-Materials. Energies, 9(6), 394. https://doi.org/10.3390/en9060394