Dynamic Energy Management of Hybrid Energy Storage Systems with a Hierarchical Structure
Abstract
:1. Introduction
2. System Description and Modeling
2.1. PV System Modeling
2.2. Storage Battery Modeling
2.3. Supercapacitor Modeling
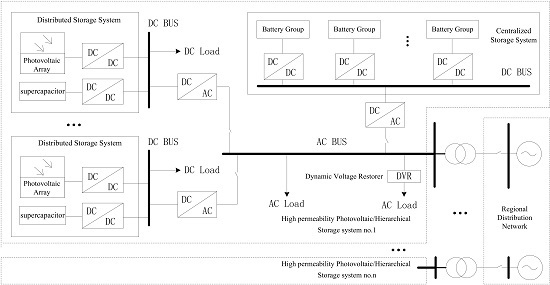
2.4. Hierarchical Structure
3. Control Method
3.1. Control of a Single DC Bus Voltage
3.2. Control of System
3.3. Constraint Condition
3.4. Centralized Management of Mass Batteries
4. Simulation
4.1. Single Control for a Short Time Scale
4.2. Single Control for a Long Time Scale
4.3. Control of Three Distributed Storage Systems
5. Conclusions and Prospects
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| current of photo-generated current source | |
| internal parallel resistance of silicon solar cells | |
| internal series resistance of silicon solar cells | |
| output current of photovoltaic | |
| output voltage of photovoltaic | |
| diode saturation current | |
| a constant ( ) | |
| Boltzmann constant ( ) | |
| absolute temperature when photovoltaic works | |
| diode feature fitting coefficient | |
| the actual irradiance | |
| irradiance at standard condition | |
| absolute temperature when photovoltaic works at standard condition | |
| temperature coefficient | |
| photo-generated current at standard condition | |
| E | no-load voltage |
| battery constant voltage | |
| K | polarisation voltage |
| Q | battery capacity |
| actual battery charge | |
| A | exponential zone amplitude |
| B | exponential zone time constant inverse |
| battery voltage | |
| battery current | |
| reference value of inverter power | |
| AC load power | |
| power of load and inverter | |
| reference power of storage system | |
| actual power of photovoltaic | |
| reference power of supercapacitor | |
| reference power of battery | |
| supercapacitor voltage | |
| reference value of battery current | |
| reference value of supercapacitor current | |
| DC bus voltage | |
| duty ratio of PWM control | |
| time constant of low pass filter | |
| the total number of photovoltaic | |
| output power of each energy storage | |
| total number of energy storages | |
| tie-line power of other power grids | |
| rated voltage of bus-bar | |
| actual voltage of bus-bar | |
| , | inferior and superior limit of power for photovoltaic |
| , | inferior and superior limit of power for batteries |
| , | inferior and superior limit of power for supercapacitor |
| initial SOC of battery | |
| rated capacity of battery | |
| influence factor of battery capacity | |
| battery efficiency | |
| actual SOC of battery | |
| actual SOC of supercapacitor | |
| actual voltage of supercapacitor | |
| max allowable voltage of supercapacitor | |
| , | inferior and superior limit of SOC for batteries |
| , | inferior and superior limit of SOC for supercapacitor |
| power of DC load | |
| , , | power of DC load 1, 2, 3 |
References
- Yang, W.; Xia, Z.; Feng, X. Impacts of large scale and high voltage level photovoltaic penetration on the security and stability of power system. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference (APPEEC), Chengdu, China, 28–31 March 2010; pp. 1–5.
- Srivastava, A.K.; Kumar, A.A.; Schulz, N.N. Impact of distributed generations with energy storage devices on the electric grid. IEEE Syst. J. 2012, 6, 110–116. [Google Scholar] [CrossRef]
- Hill, C.A.; Such, C.S.; Chen, D. Battery energy storage for enabling integration of distributed solar power generation. IEEE Trans. Smart Grid 2012, 3, 850–857. [Google Scholar] [CrossRef]
- Kim, S.-T.; Bae, S.H. Energy management based on the photovoltaic HPCS with an energy storage device. IEEE Trans. Ind. Electron 2015, 62, 4608–4617. [Google Scholar] [CrossRef]
- Ge, B.; Abu-Rub, H. An Energy-stored quasi-z-source inverter for application to photovoltaic power system. IEEE Trans. Ind. Electron 2013, 60, 4468–4480. [Google Scholar] [CrossRef]
- Reddy, S.S.; Momoh, J.A. Realistic and transparent optimum scheduling strategy for hybrid power system. IEEE Trans. Smart Grid 2015, 6, 3114–3124. [Google Scholar] [CrossRef]
- Sun, K.; Xing, Y.; Guerrero, J.M. A distributed control strategy based on DC bus signaling for modular photovoltaic generation systems with battery energy storage. IEEE Trans. Power Electron 2011, 26, 3032–3045. [Google Scholar] [CrossRef]
- Liu, X.; Aichhorn, A. Coordinated Control of distributed energy storage system with tap changer transformers for voltage rise mitigation under high photovoltaic penetration. IEEE Trans. Smart Grid 2012, 3, 897–906. [Google Scholar] [CrossRef]
- Kabir, M.N.; Mishra, Y.; Ledwich, G. Coordinated control of grid-connected photovoltaic reactive power and battery energy storage systems to improve the voltage profile of a residential distribution feeder. IEEE Trans. Ind. Inform. 2014, 10, 967–977. [Google Scholar] [CrossRef]
- Lampropoulos, L.; Garoufalis, P.; Paul, P.J. Hierarchical predictive control scheme for distributed energy storage integrated with residential demand and photovoltaic generation. IET Gener. Transm. Distrib. 2014, 9, 2319–2327. [Google Scholar] [CrossRef]
- Tummuru, N.R.; Mishra, M.K.; Srinivas, S. Dynamic energy management of hybrid energy storage system with high-gain PV converter. IEEE Trans. Energy Convers. 2015, 30, 150–160. [Google Scholar] [CrossRef]
- Feng, X.; Gooi, H.B.; Chen, S.X. Hybrid energy storage with multimode fuzzy power allocator for PV systems. IEEE Trans. Sustain. Energy 2014, 5, 389–397. [Google Scholar] [CrossRef]
- Wang, G.; Ciobotaru, M.; Agelidis, G.A. Power smoothing of large solar PV plant using hybrid energy storage. IEEE Trans. Sustain. Energy 2014, 5, 834–842. [Google Scholar] [CrossRef]
- Zubieta, L.; Bonert, R. Characterization of double-layer capacitors (DLCs) for power electronics applications. IEEE Trans. Ind. Appl. 2000, 36, 199–205. [Google Scholar] [CrossRef]
- Komori, M.; Uchimura, Y. Improving the dynamics of two types of flywheel energy storage systems with SMBs. IEEE Trans. Appl. Supercond. 2005, 15, 2261–2264. [Google Scholar] [CrossRef]
- Lifshitz, D.; Weiss, G. Optimal control of a capacitor-type energy storage system. IEEE Trans. Autom. Control 2015, 60, 216–220. [Google Scholar] [CrossRef]
- Pei, L.; Huang, Z.; Dong, D. A hierarchical management system for energy storage batteries. Energy Storage Sci. Technol. 2014, 3, 416–422. [Google Scholar]
- Wang, S.; Zhang, N. Photovoltaic system power forecasting based on combined grey model and BP Neural network. In Proceedings of the International Conference on Electrical and Control Engineering (ICECE), Yichang, China, 16–18 September 2011; pp. 4623–4626.













| Storage Battery | Supercapacitor | ||
|---|---|---|---|
| Rated Voltage | 3.6 V | 270 F | |
| Maximum Voltage | 4.2 V | 190 F/V | |
| Capacity | 1 Ah | 100 F | |
| Control Parameters | 220 F | ||
| Storage Battery | P = 35, I = 1.2 × 105 | 2.5 mΩ | |
| Supercapacitor | P = 45, I = 1.2 × 105 | 0.9 Ω | |
| DC Bus Voltage | 700 V | 5.2 Ω | |
| DC Bus Voltage | Load Power | ||
|---|---|---|---|
| DC Bus 1 | 220 V | 24.2 kW | |
| DC Bus 2 | 220 V | 48.4 kW | |
| DC Bus 3 | 220 V | 30.25 kW | |
| DC Bus 4 | 700 V | / | |
| Supercapacitor | |||
| Series Number | 50 | Parallel Number | 2 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, C.; Miao, S.; Lei, Q.; Li, Y. Dynamic Energy Management of Hybrid Energy Storage Systems with a Hierarchical Structure. Energies 2016, 9, 395. https://doi.org/10.3390/en9060395
Ye C, Miao S, Lei Q, Li Y. Dynamic Energy Management of Hybrid Energy Storage Systems with a Hierarchical Structure. Energies. 2016; 9(6):395. https://doi.org/10.3390/en9060395
Chicago/Turabian StyleYe, Chang, Shihong Miao, Qi Lei, and Yaowang Li. 2016. "Dynamic Energy Management of Hybrid Energy Storage Systems with a Hierarchical Structure" Energies 9, no. 6: 395. https://doi.org/10.3390/en9060395
APA StyleYe, C., Miao, S., Lei, Q., & Li, Y. (2016). Dynamic Energy Management of Hybrid Energy Storage Systems with a Hierarchical Structure. Energies, 9(6), 395. https://doi.org/10.3390/en9060395