A Least Squares Support Vector Machine Optimized by Cloud-Based Evolutionary Algorithm for Wind Power Generation Prediction

Abstract

Accurate wind power generation prediction, which has positive implications for making full use of wind energy, seems still a critical issue and a huge challenge. In this paper, a novel hybrid approach has been proposed for wind power generation forecasting in the light of Cloud-Based Evolutionary Algorithm (CBEA) and Least Squares Support Vector Machine (LSSVM). In order to improve the forecasting precision, a two-way comparison approach is conducted to preprocess the original wind power generation data. The pertinent parameters of LSSVM are optimized by using CBEA to verify the learning and generalization abilities of the LSSVM model. The experimental results indicate that the forecasting performance of the proposed model is better than the single LSSVM model and all of the other models for comparison. Moreover, the paired-sample t-test is employed to cast light on the applicability of the developed model.

1. Introduction

The utilization of wind energy for electric power systems offers an alternative to decrease the dependence on fuel-based energy, effectively alleviating the environmental pressure [1]. However, the exponential development of wind power creates a number of challenges for wind industry dramatically [2]. Enhancing the reliability of wind power generation, which is often affected adversely by the variability of wind speed, temperature and other factors, can be one of the major challenges [3]. The volatility of wind power impacts the stability of power system and increases the operational cost of power systems [4]. Thus, high precision in wind power generation prediction allows for better planning for unit commitment and economic dispatch [5], the security of the running systems [6], and other relevant procedures.

In the past few years, there has been a large body of research on wind power prediction algorithms. These studies include, but are not limited to, wind speed prediction, generated energy and generated power forecasting. The methods can be mainly divided into four types: physical methods [7], statistical methods, intelligent methods, and hybrid methods [8]. The physical approaches are mainly utilized for long-term forecasting [9]. The statistical approaches, which are time series-based methods, apply mathematical and statistical models, including Vector Autoregressive (VAR) models [10], Autoregressive Moving Average (ARMA) models, Autoregressive Integrated Moving Average (ARIMA) models, Kalman Filters (KF) [11], etc., to achieve the prediction of wind speed and wind power [12]. Erdem [13] introduced a combined forecasting method based on an ARMA model to estimate wind speed and direction. Liu [14] performed wind speed forecasting using an Autoregressive Moving Average-Generalized Autoregressive Conditional Heteroscedasticity model (ARMA-GARCH). The experimental findings indicated that the persistence model effectively caught all the features of wind speed. Liu [15] employed an ARIMA model to decide the optimal network structures of an Artificial Neutral Network (ANN) model and choose the initial parameters of the Kalman Filter (KF) models. The results demonstrated that the KF or ANN models combined with the ARIMA models had better forecasting performance than the corresponding single KF or ANN models. Although the statistical methods display good performance in short-term forecasting [8], these models are typically linear with solely the historical values of the predicted variable being regarded as the input [16]. Therefore, the utilization of statistical models for wind power prediction seems problematic owing to their poor nonlinear fitting ability [17].

In most cases, intelligent algorithms with the adaptive and self-organized learning features noticeably provide good results for the estimation of nonlinear time series. For instance, Artificial Neural Networks (ANN) [18,19] and Least Squares Support Vector Machine (LSSVM) are considered efficient approaches due to their remarkable nonlinear mapping capabilities for wind power prediction, and the LSSVM methods have been successfully utilized in many other applications [20,21]. In addition, neural fuzzy network [22], fuzzy logic [23], fuzzy-inference [24], and data-driven approach [25] are also used for wind power prediction. A mixed Seasonal Auto-regression Integrated Moving Average and Least Square Support Vector Machine (SARIMA-LSSVM) model was established by Guo [26] to forecast the monthly wind speeds. Experimental results and the hypothesis tests indicated that the method was simple and rather operative. Using historical data and numerical weather predictions, a comparative study of wind power generation prediction was conducted, and the results suggested that the hybrid approach based on wavelet decomposition with LSSVM clearly was superior to the hybrid Artificial Neural Network (ANN)-based methods [27]. Yuan [28] developed a LSSVM model on the basis of Gravitational Search Algorithm (GSA) for short-term wind power forecasting. The simulation results revealed that the hybrid LSSVM-GSA model had higher precision for short-term wind power prediction when compared to the Back Propagation Neural Network (BPNN) and Support Vector Machine (SVM) model.

Recently, least squares support machine approaches have attracted considerable attention from many experts and scholars. Integrated with various evolutionary methods, a wealth of research has built various LSSVM models to obtain better results since the prediction performance of the LSSVM model relies on the regularization parameter and the kernel parameter in LSSVM. Sun [29] proposed a LSSVM model optimized by Particle Swarm Optimization (PSO). The experimental results showed that the method can evidently improve the forecasting precision. Wang [30] constructed a LSSVM model with the parameters being optimized by the PSO and Simulated Annealing (PSOSA). A case study from four wind farms in China was utilized to verify the validity of the hybrid model. Mahjoob [31] designed a Genetic Algorithm-Least Squares Support Vector Machine (GA-LSSVM) model to predict the short-term market clearing prices in competitive power markets. Jung [32] introduced a novel LSSVM method by combining the Direct Search Optimization (DSO) algorithm and Genetic Algorithm (GA) for faster computing speed and higher forecasting precision.

From the previous research it can be concluded that the local optimum and premature convergence issues may arise from the PSO and GA methods in the process of parameter selection. In this study, a novel evolutionary algorithm was adopted, namely the Cloud-Based Evolutionary Algorithm (CBEA), put forward by Zhang [33] in 2008, which uses the outstanding characteristics of the cloud model in the process of transforming a qualitative concept to a set of quantitative numerical values [34], combined with the basic principles of evolutionary computing. CBEA can model the inheritance and mutation of species naturally and uniformly by using the cloud model, which makes it easy to adaptively control the scale of mutation and inheritance, and the scope of search space. This nature endows CBEA with excellent ability to quickly obtain the optimal solution. Considering the amazing capacity of the CBEA in the process of parameter optimization, the purpose of the study reported here was to select the pertinent parameters of the LSSVM model by using the CBEA method.

Moreover, from the previous literature it can be found that the raw series may be perceived as the inputs for wind power forecasting directly with relatively little attention to data preprocessing. However, in the practical operation of wind farms, the shutdown of wind farms due to maintenance or abandoned wind, sensor faults, measurement errors and other factors may lead to abnormal or missing data [35]. The prediction accuracy and the reliability of the prediction results can be affected by using the original data in forecasting models. Therefore, it is necessary to implement the treatment of the historical data for improving wind power prediction. The efficiency of the traditional lateral comparison method tends to be very poor due to its inability to deal effectively with the loss and mutation of continuous data. With a good combination of the paramount advantages of the lateral comparison method and the vertical comparison method, a two-way comparison approach can be utilized to process the data continuously [36]. In this study, the two-way comparison approach is applied to preprocess the original wind power generation series.

Furthermore, the main purpose of the current paper is to explore an accurate prediction approach for wind power generation. A hybrid forecasting model, which is based on CBEA-LSSVM, was used to predict daily wind power generation. In order to guarantee the generalization and learning abilities of LSSVM model, the related parameters in LSSVM were optimized by the CBEA. In addition, a two-way comparison method was employed to preprocess the original wind power generation series to improve the forecasting accuracy. The focus of the present paper is on comparing the forecasting results of the CBEA-LSSVM, PSO-LSSVM, GA-LSSVM, BPNN, single LSSVM and ARMA models. Moreover, concerning that the cloud-based evolutionary algorithm has relatively more initial parameters, this paper also investigated the influence of entropy and the total evolving generation on the accuracy of CBEA-LSSVM model. Furthermore, to corroborate the effectiveness of the developed model, a case study from China was examined, and the paired-sample t-test was conducted to identify whether there was value to focus on the difference of forecasting results from the single LSSVM model and the hybrid LSSVM models.

The remainder of this study is constructed as follows: Section 2 outlines the principles of CBEA and LSSVM. Section 3 introduces a hybrid model for wind power generation prediction. In Section 4, the proposed model is tested by a case study and an in-depth comparative analysis is provided. Finally, Section 5 offers some conclusions of the research.

2. Methodology

2.1. Cloud-Based Evolutionary Algorithm

The cloud-based evolutionary algorithm is proposed on the basis of the principle of evolutionary computing [33]. Based on the excellent characteristics of the cloud model, CBEA can adaptively complete the inheritance and mutation of species by using the normal cloud generator, which can preferably address the issues of local optimal solution and premature convergence of the genetic algorithm, and effectively enhance the convergence speed.

In order to display the idea of CBEA apparently, some definitions of this technology are given as follows:

(1)

Evolving pattern. EP(Ex,En,He) is the evolving pattern described by the cloud model. Ex can be defined as the individual representing the good characteristics of ancestral inheritance. En is the evolving entropy to represent the range of mutation. He refers to the evolving hyper-entropy representing the evolving stability. Considering the parent individual (Ex) as the mother individual, we initialize the evolving entropy and the evolving hyper-entropy, then a population can be obtained from the cloud droplets generated by using the normal cloud generator. Therefore, the evolving pattern can be defined as the generating model of population.

(2)

Evolvement. Regarding the superior individual with better fitness value in the population as the mother individual, evolvement refers to the operation to generate a new population according to evolving pattern.

(3)

Mutation. Mutation is the operation where an excellent individual who abandons all or part of the father’s generation in the process of evolution, and can generate new individual on the basis of some certain strategies as the mother individual to produce the new population.

(4)

Evolving generation. A generation of the new community in the process of evolution is called an evolving generation.

(5)

Elite individual. Elite individuals, which are the most adaptable individuals in the evolvement process, can be classified into two types: the present elite individual and the cross generation elite individual. The present elite individual is the most adaptable individual in an evolving generation, and the cross generation elite individual is the most adaptable individual in different evolving generations. The successive common generation is that there is not cross generation elite continuously. Conversely, the successive excellent generations are that there are cross generation elites continuously.

(6)

Evolving strategy. Evolving strategy is the controlling strategy of evolvement in the process of evolution. Through the development of evolving strategy, two problems can be solved:

(a)

Local refinement. When there is a cross generation elite, the new extreme neighborhood can be found and the local refinement operation need to be carried out. The specific method is that the evolving range should be decreased (reduce En) and the stability should be augmented (reduce He). For instance, En and He can be set to the original values of 1/K, and K is the evolving coefficient greater than 1;

(b)

Local change (evolving variation). When the successive common generative reaches a certain threshold (λ_local), the algorithm may fall into a local optimal neighborhood. At this time, it needs to jump out of the local, and try to find a new local optimal. For instance, En and He can be L times larger than the original values, L is the evolving coefficient of variation. When the local optimal values of the function are very close, the evolutionary mutation can find the global optimal value in the local optimal values.

(7)

Mutation strategy. Mutation strategy is the controlling strategy of mutation operation in the process of evolution, which is the guarantee of getting rid of the local optimum. When the better individual cannot be obtained through several evolving generations and the evolving variation seems ineffective, the mutation operation needs to be conducted. The relationship between the threshold of local change and mutation is λ_global > λ_local. Mutation operation is used to find a new extreme area in the global scope. Correspondingly, the threshold of mutation can be defined as the threshold of global mutation (λ_global ).

Moreover, in the CBEA method the evolvement and the mutation are unified, and the evolving variation is the fusion of the evolvement and the mutation, which can be used for local refinement or jumping out local optimum. Mutation is applied to find a new search area of extreme value in the global scope. The CBEA can identify the current state of evolution, and then can be adjusted adaptively. Thus, the CBEA can obtain the global optimum in the process of evolvement.

Similar to most of evolutionary computation techniques, the computational process of CBEA can be described as follows:

Step 1:

The system is initialized to a set of random solutions, namely, the value of the individual in the community.

Step 2:

Calculate the fitness value of all individuals, and select the first m of the elite individuals, constituting the elite individual vector.

Step 3:

The first m individuals breed a population separately.

Step 4:

The elite individual is the optimal solution when the algorithm reaches the maximum evolving generation, otherwise the algorithm returns Step 2.

2.2. Least Squares Support Vector Machine

LSSVM [37] is a variation of the standard Support Vector Machine (SVM) which uses square errors in the cost function and equality constraints. Consider the training sample set S = {(x_i,y_j); i = 1,2,3…,t} (x_i = Rⁿ, y_i = R). Then, the optimal decision function can be constructed by mapping the input space into the high-dimension feature space as follows:

$$f\left(x\right)={\mathsf{\omega }}^T\mathsf{\phi }\left(x\right)+b$$

(1)

where $\mathsf{\phi }\left(x\right)$ is the nonlinear function; ω is the weight; b is the bias to be solved.

The structural risk minimization is:

$$R=\frac{1}{2}||\mathsf{\omega }|{|}^2+\mathsf{\gamma }{R}_{\text{emp}}$$

(2)

where $||\mathsf{\omega }|{|}^2$ represents the model complexity, $\mathsf{\gamma }$ is the regularization parameter to balance the complex degree and approximation accuracy of the model, R_emp denotes the empirical risk function, the objective function of LSSVM can be framed:

$$\min Z(\mathsf{\omega },\mathsf{\xi })=\frac{1}{2}||\mathsf{\omega }|{|}^2+\mathsf{\gamma }{\displaystyle \sum _{i=1}^t{\mathsf{\xi }}_i^2}$$

$$s.t.y_i=\mathsf{\omega }\mathsf{\phi }(x_i)+{\mathsf{\xi }}_i+b,i=1,2,3,\cdots ,t$$

(3)

where ${\mathsf{\xi }}_i$ is the error variable, the corresponding Lagrange function is expressed:

$$L(\mathsf{\omega },b,\mathsf{\xi },\mathsf{\lambda })=\frac{1}{2}||\mathsf{\omega }|{|}^2+\mathsf{\gamma }{\displaystyle \sum _{i=1}^t{\mathsf{\xi }}_i^2}-{\displaystyle \sum _{i=1}^t{\mathsf{\lambda }}_i}(\mathsf{\omega }\mathsf{\phi }(x_i)+{\mathsf{\xi }}_i+b-y_i)$$

(4)

where λ_i(1,2,3,…,t) are the Lagrange multipliers.

According to the Karush-Kuhn-Tucker (KKT) conditions, Equation (5) is given by:

$$\{\begin{array}{l}\mathsf{\omega }-{\displaystyle \sum _{i=1}^t{\mathsf{\lambda }}_i}{\mathsf{\xi }}_i^2=0,\\ {\displaystyle \sum _{i=1}^t{\mathsf{\lambda }}_i}=0,\\ {\mathsf{\lambda }}_i-{\mathsf{\gamma }\mathsf{\xi }}_i=0,\\ \mathsf{\omega }\mathsf{\phi }(x_i)+{\mathsf{\xi }}_i+b-y_i=0.\end{array}$$

(5)

Based on Equation (5), the optimization problem can be transformed into a linear equation set:

$$\left[\begin{array}{cc}0& I^T\\ I& J+\frac{I}{\mathsf{\gamma }}\end{array}\right]\left[\begin{array}{c}b\\ \mathsf{\lambda }\end{array}\right]=\left[\begin{array}{c}0\\ y\end{array}\right]$$

(6)

where I = [11…1]^T is a $t\times 1$ dimensional vector, λ = [λ₁ λ₂…λ_t]^T, y = [y₁ y₂…y_t]^T, $J_{ij}=\mathsf{\phi }{(x_i)}^T\mathsf{\phi }(x_j)=K(x_i,x_j)$, K is the kernel function on the basis of the Mercer’s condition, the regression function of LSSVM model can be described as:

$$f(x)={\displaystyle \sum _{i=1}^t{\mathsf{\lambda }}_i}K(x_i,x_j)+b$$

(7)

In this study, the Gaussian radial basis function is selected as the kernel function, which is shown as the following equation:

$$K(x_i,x_j)=\exp \left[\frac{-||x_i-x_j|{|}^2}{2{\mathsf{\sigma }}^2}\right]$$

(8)

where σ² is the kernel parameter.

In addition, from the training problem of LSSVM, it can be seen that the regularization parameter (γ) and the kernel parameter (σ²) may affect the generalization performance of the LSSVM model. Contrary to experimental comparison, grid searching and cross validation approaches used in previous research, in this study the two parameters of the proposed LSSVM model are optimized by using a CBEA to minimize the generalization error.

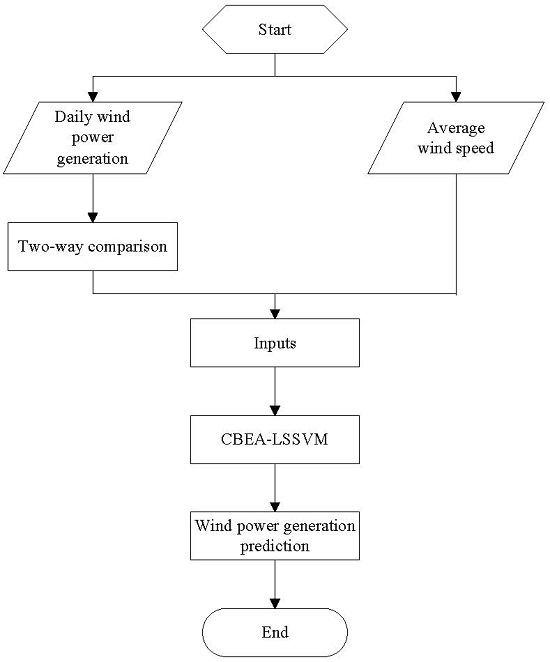
3. Approach of CBEA-LSSVM Model

In the light of the predominant features of the cloud model and the basic principle of evolutionary computing, CBEA can quickly obtain the optimal strategy through controlling the scale of mutation and inheritance, and the scope of search space adaptively. The following procedures constitute the CBEA-LSSVM algorithm.

(1)

Select the training set and the testing set.

(2)

Set the scope of the parameters (γ, σ²) to be trained.

(3)

The initial value of the evolutionary pattern (EP(Ex,En,He)) of CBEA-LSSVM can be determined according to Step (2), and En should be as large as possible, He ≥ 0.05; Set the scale of the community n, the size of the community richness m, the scale vector of the population V, the threshold of global mutation λ_global, the threshold of local mutation λ_local, the total evolving generation P, the evolving coefficient K, the evolving coefficient of variation L, and the fitness function f.

(4)

Generate the initial community using EP(Ex,En,He).

(5)

A series of prediction models can be obtained by placing all individual values of the community into Equation (7), and the prediction results can be attained by taking the sample as the input.

(6)

Calculate the fitness values of all individuals in the community by placing the predicted values into the fitness function, and eliminate the population in accordance with certain conditions.

(7)

Choose m elite individuals according to the size of fitness value and the requirement of control strategy, and record the successive common generation g_c, the successive excellent generation g_e.

(8)

Compare the size of g_e and 0. If g_e > 0, then it indicates that the individual is in the extreme neighborhood. Thus, the local refinement should be implemented, that is, to decrease the evolutionary scope (reduce En), to increase the stability (reduce He), and to expand the search accuracy and constancy.

(9)

If g_c > λ_global, then the mutation operation should be performed.

(10)

If g_c > λ_local, it shows that the individual can reach the local optimum. Then, the local change operation should be carried out by improving En and He.

(11)

Compute the new En and the new He, and the value of the elite individual regarded as Ex would be placed into the normal cloud generator to produce a new population.

(12)

Compare the evolving generation Q and the total evolving generation P. If Q < P, return to step (5). Otherwise, record the built group $E_{X_Q}$, and compare the fitness of all built groups to select the optimal individual. Then, $E_{X_Q}$ is the optimal parameter of local refinement.

(13)

The optimal forecasting model can be obtained with the optimal parameter vector $E_{X_Q}$ being brought into Equation (7).

(14)

The predicted values of the testing set can be gained by using the optimal forecasting model.

In brief, Figure 1 distinctly illustrates the flowchart of CBEA-LSSVM algorithm. The model in this case only has one input which represents the value of the exogenous variables. This paper selects the average wind speed as the experimental variable for the input of LSSVM with daily wind power generation. The output variable of the proposed model in this study is daily wind power generation. The two-way comparison method is employed to preprocess historical wind power generation series, and the LSSVM approach is applied to model the training set with the root mean square error between real value and predictive value being regarded as the fitness function of CBEA. The relative parameters in LSSVM are automatically fine-tuned by using CBEA for searching the minimum fitness value. The LSSVM model with optimal parameters can be utilized to forecast wind power generation. The flowchart of the proposed model is given in Figure 2.

4. Case Study

4.1. Data Sets

This paper collects the historical data of a wind farm located in Hebei Province in China. Three hundred and one (301) daily observations from 5 January 2015 to 1 November 2015 are selected to demonstrate the powerful performance of the proposed model. The daily measurement of the exogenous variable of this period is daily average wind speed. The meteorological data, which is daily average wind speed, have been obtained from the Supervisory Control And Data Acquisition (SCADA) System of the wind farm. The wind speed measurement height is 65 m. The first 220 values are used as the training sample, and the remaining values are chosen as the testing set. As time goes by, the training sample set moves forward. The forecasting results and the actual wind power generation data of prediction period can be compared.

4.2. Data Preprocessing

In the actual operation of wind farms, the phenomenon of abnormal data or missing data may occur due to maintenance, abandoned wind, sensor fault, measurement error and other factors [35]. The prediction accuracy and the reliability of the results may be adversely affected by using the original data in forecasting models. Thus, the pretreatment of the historical data for wind power prediction continues to attract considerable attention.

4.2.1. Pretreatment of Abnormal Data

In this research, a two-way comparison method [36] is employed to identify the abnormal data due to the inability of manual work to find the wrong data in a massive dataset. The two-way comparison approach can improve the situation where the traditional lateral comparison method cannot effectively deal with the loss and mutation of continuous data in the process of judgment and correction of abnormal data. The flowchart of the two-way comparison method is shown in Figure 3.

The raw data and the processed data are given in Figure 4 and Figure 5, respectively. The definition of the two-way comparison method can be described by the following equations:

$$\mathsf{\delta }(t)=\frac{{\displaystyle \sum _{i=1}^n|P(i,t)-P(i,t-1)|}}{n}$$

(9)

$$|P(i,t)-P(i,t-1)|\ge \mathsf{\epsilon }\cdot \mathsf{\delta }(t)$$

(10)

$$\left|\frac{P(i,t)-P(i,t-1)}{P(i,t-1)}\right|\ge 0.05$$

(11)

$$P^{\prime }(i,t)=\frac{{\displaystyle \sum _{j=1}^{k}P(j,t)}}{k}$$

(12)

where P(i,t) is the power generation of the t-th day in the i-th month, the threshold δ(t) is the mean of variation of n months on the t-th day, P(j,t) is the normal data by judgment on the t-th, k is the number of normal data on the t-th day, P’(i,t) is the corrected data, ε is the artificially prescribed parameters. In this work, ε = 0.09. The degree of identification and correction can be changed by adjusting the size of ε, the greater the value, the lower the degree of correction.

From Figure 4, it can be seen that there are some continuous zeros, successively missing values and mutation values, demonstrating that there exist some abnormal data and the raw data is very poor. Figure 5 displays the corrected wind power generation series using the two-way comparison method, which provides an effective sample set for the following prediction work.

4.2.2. Data Normalization

This paper adopts the following equation [38] to complete the linear transformation to [0,1]:

$$\stackrel{\_\_}{x_i}=\frac{x_i-x_{\min }}{x_{\max }-x_{\min }}$$

(13)

where $\stackrel{\_\_}{x_i}$ represents the normalization of the original data; $x_{\max }$ and $x_{\min }$ represent the maximum and minimum of the original data, respectively.

4.3. Evaluation Criteria of Prediction Accuracy

To compare the forecasting performance of models effectively, this study selects Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE) and the coefficient of determination (R²) to measure the precision of the models involved in this paper. R² ∈ [0,1]. The closer the value of R² is to 1, the better the performance of the model. The equations of the aforementioned criteria are shown as follows:

$$\text{RMSE}=\sqrt{\frac{1}{n}{{\displaystyle \sum _{i=1}^n\left(y_i-\stackrel{\wedge }{y_i}\right)}}^2}$$

(14)

$$\text{MAE}=\frac{1}{n}{\displaystyle \sum _{i=1}^n|y_i-{\stackrel{\wedge }{y}}_i|}$$

(15)

$$\text{MAPE}=\frac{1}{n}{\displaystyle \sum _{i=1}^n|\frac{y_i-{\stackrel{\wedge }{y}}_i}{y_i}|}$$

(16)

$$R^2=1-\frac{{\displaystyle \sum _{i=1}^n{({\stackrel{\wedge }{y}}_i-{\mathrm{y}}_i)}^2}}{{\displaystyle \sum _{i=1}^n{({\stackrel{\wedge }{y}}_i-\overline{y})}^2}}$$

(17)

where y_i is the real value on the i-th day; ${\widehat{y}}_i$ denotes the predicted value; $\overline{y}$ represents the average value of the predicted value.

4.4. Result Analysis of CBEA-LSSVM

Since the relative parameters of the LSSVM model play a pivotal role in the forecasting performance, the regularization parameter $(\mathsf{\gamma })$ and kernel parameter $({\mathsf{\sigma }}^2)$ are optimized by using CBEA method with exciting search ability. The main parameters of the CBEA are listed in

Table 1. Main parameters of CBEA.

Parameters	Values	Parameters	Values
Entropy (En)	$\left[61.8,61.8\right]$	Total evolving generation (P)	20
Hyper-entropy (He)	$\left[0.05,0.05\right]$	Evolving coefficient (K)	10
Scale of the community (n)	100	Evolving coefficient of variation (L)	$\sqrt{10}$
Threshold of global mutation (λglobal)	6	Size of the community richness (m)	10
Threshold of local mutation (λlocal)	2

.

Moreover, given that the forecasting error is the standard of evaluating the model performance, the fitness function of this study can be described as follows:

$$f=\sqrt{\frac{1}{k}{{\displaystyle \sum _{i=1}^k\left(y_i-\stackrel{\wedge }{y_i}\right)}}^2}$$

(18)

In order to improve the variation characteristics of the evolutionary algorithm, the scale vector of the population V can be set to a function of the fitness value:

$$V=[\frac{n}{m}+(\frac{{\displaystyle \sum _{i=1}^m{f}_i}}{m}-f_i)\times n,\cdots ,\frac{n}{m}+(\frac{{\displaystyle \sum _{i=1}^m{f}_i}}{m}-f_m)\times n]$$

(19)

Furthermore, when implementing the mutation operation, $E_{x_i}$ can be perceived as the mean of elite individual of historical cross generation in the i th population to search the optimal individual easily. To reduce the extreme range and make the algorithm converge fast, En and He can be set as 1/K of the original values when conducting the local refinement. When executing the local change operation, En and He are L times larger than the original values to expand the scope of evolution and dispersion and search new local optimum.

Finally, the testing set is used to determine the prediction performance of the LSSVM model with the optimal parameters obtained by the CBEA. Figure 6 displays the prediction errors of the proposed model. From Figure 6, it is clear that the changing trend of errors can be relatively steady. Merely two errors exceed 3. Moreover, the maximum value among all errors is 4.1406.

4.5. Comparative Analysis

4.5.1. Analysis of CBEA-LSSVM with Various Parameters

Considering that the cloud-based evolutionary algorithm has relatively more initial parameters, this paper investigates the impacts of entropy (En) and the total evolving generation (P) on the accuracy of the prediction model. Regarding different parameters of CBEA, the forecasting results of CBEA-LSSVM can be shown in Figure 7.

In order to accurately measure the accuracy of the model prediction, the prediction results with different parameters are listed in

Table 2. The prediction results of CBEA-LSSVM with different parameters.

CBEA-LSSVM	Indices
	RMSE (10 MWh)	MAE(10 MWh)	MAPE (%)	R2
En = [0.618,0.618] P = 20	2.2762	2.1491	20.17	0.9910
En = [0.618,0.618] P = 10	1.9093	1.7007	14.51	0.9932
En = [61.8,61.8] P = 10	1.7266	1.6182	13.59	0.9939
En = [61.8,61.8] P = 20	1.3798	1.1281	8.10	0.9951

. Comparing Figure 7a,b, it suggests that the total evolving generation should be reduced and the predicted result curve is more approximate to the actual curve when the entropy of the cloud is smaller. Comparing Figure 7a,d, it indicates that the prediction results curve is closer to the actual curve and the prediction performance seems better when the entropy of the cloud is larger. From Figure 7c,d, it can be seen that the total evolving generation can be increased and the prediction results curve is closer to the actual cure when the entropy of the cloud is equal.

Moreover, from Table 2 it can be concluded that the forecasting accuracy of the proposed model seems better since the individual randomness with greater entropy may be larger. For instance, under the circumstance of the same evolving generation (P = 20), the MAPE of CBEA-LSSVM with En = [61.8,61.8] is 8.10%, but the MAPE of CBEA-LSSVM with En = [0.618,0.618] is 20.17%. Also, the RMSE of CBEA-LSSVM with En = [61.8,61.8] is 1.3798, but the RMSE of CBEA-LSSVM with En = [0.618,0.618] is 2.2762.

4.5.2. Analysis of Different Forecasting Models

In this study, diverse evolutionary algorithms, which are Cloud-Based Evolutionary Algorithm (CBEA), Particle Swarm Optimization (PSO) and Genetic Algorithm (GA), are employed to optimize the related parameters of LSSVM models in order to corroborate the excellent performance of the developed model effectively. Moreover, the single LSSVM model, ARMA, and Back Propagation Neutral Network (BPNN) are built to forecast wind power generation for comparison. The LSSVM model combined with the CBEA method performs best when compared to the other forecasting models.

The obtained parameters of the LSSVM models referred to this study are listed in

Table 3. The optimal parameters of LSSVM models.

Parameters	Forecasting Methods
	CBEA-LSSVM	PSO-LSSVM	GA-LSSVM	LSSVM
γ	0.0583	3.6119	12.8347	10.2634
σ2	0.3376	0.3247	1.0216	0.1368

. Regarding PSO-LSSVM, the max-iteration number of PSO is 200, the size of population is 40, and the inertia weight is random number w = rand(0,1). With respect to GA-LSSVM, the size of population is 50, the total evolving generation is 100, the mutation probability is 0.09, and the crossover probability is 0.90. In terms of BPNN, the number of neuron in hidden layer is 15, and the learning rate is 0.035. Regarding the single LSSVM model, the grid searching method and cross validation approach are applied to select the optimal regularization parameter and the kernel parameter. For the grid searching method, γ = 2⁻¹⁰–2¹⁵, the step of γ is 1; σ² = 2¹⁵–2⁻¹⁰, and the step of σ² is 1.

Moreover,

Table 4. The computing time about different approaches.

Computing Time (s)	Forecasting Methods
	CBEA-LSSVM	PSO-LSSVM	GA-LSSVM	LSSVM	BPNN	ARMA
Time	8.901	190.137	117.41	4.992	13.077	0.925

shows the computing time about different approaches. In this paper, a computer equipped with an Intel^® Core™ i3-3110M processor CPU @ 2.40 GHz, 4 GB RAM and the 64 bit Windows 7 operating system (OS) was utilized. In addition, this paper employed MATLAB R2014a to write all programs. From Table 4, in comparison with PSO-LSSVM and GA-LSSVM, the forecasting time of CBEA-LSSVM is smaller, which means that CBEA can effectively decrease the running time of parameter optimization while improving the LSSVM prediction accuracy. The single models such as ARMA and LSSVM take less time compared with the hybrid models, however, the prediction accuracy of single models is lower than that of the hybrid models. Hence, it is reasonable to adopt more accurate wind power generation approaches taking a little more time for the security of the power system. In addition, the computing time of CBEA-LSSVM is lower than that of BPNN distinctly. On the whole, the execution efficiency of CBEA-LSSVM seems relatively high.

Furthermore, in order to illustrate the robustness of CBEA-LSSVM,

Table 5. The change of the related parameters of the proposed CBEA-LSSVM model in each evolving generation.

Evolving Generation	γ	σ2	Evolving Generation	γ	σ2
1	0.0884	0.3756	11	0.0588	0.3386
2	0.0872	0.3716	12	0.0587	0.3384
3	0.0803	0.3651	13	0.0585	0.3382
4	0.0782	0.3657	14	0.0584	0.3383
5	0.0702	0.3645	15	0.0583	0.3380
6	0.0622	0.3635	16	0.0582	0.3378
7	0.0604	0.3609	17	0.0583	0.3376
8	0.0596	0.3576	18	0.0583	0.3376
9	0.0590	0.3514	19	0.0583	0.3376
10	0.0589	0.3387	20	0.0583	0.3376

displays the evolution process of the relevant parameters. The total evolving generations of the proposed CBEA-LSSVM model is 20. As shown in Table 5, the regularization parameter and the kernel parameter are close to the optimal solution when the evolving generation is 10. When the evolving generation is 15, the regularization parameter reaches the optimal value. The kernel parameter attains the optimal value when the evolving generation is 17. Thus, it can be seen that CBEA has strong robustness.

Then, daily wind power generation can be predicted by using the above approaches, and the forecasting results with various models are described in Figure 8.

Table 6. The comparison of forecasting results with different models.

Indices	Forecasting Approaches
	CBEA-LSSVM	PSO-LSSVM	GA-LSSVM	LSSVM	BPNN	ARMA
RMSE (10 MWh)	1.3798	2.1846	2.8698	3.4578	3.8507	5.3420
MAE (10 MWh)	1.1281	2.0612	2.6423	3.2496	3.4200	3.9939
MAPE (%)	8.10	19.71	26.98	31.11	33.46	46.12
$R^2$	0.9951	0.9883	0.9734	0.8875	0.8579	0.8253

shows the comparison of forecasting results with different models.

From Figure 8, it can be seen that the absolute errors between the real values and the predicted values are different using various prediction methods. In light of Figure 8a, it can be found that ARMA with merely using its own historical data may perform worst among these models for predicting wind power generation series. Conversely, the predicted values obtained by CBEA-LSSVM may be acceptable, capturing the characteristics of the original data. According to Figure 8b, compared with the single LSSVM model, the hybrid LSSVM models based on different evolutionary algorithms manifest superiority in forecasting wind power generation. Noticeably, the CBEA-LSSVM approach has better forecasting ability than PSO-LSSVM and GA-LSSVM. The following conclusions can be drawn from Table 6:

(1)

Among the three hybrid LSSVM models, the forecasting performance of CBEA-LSSVM is superior to GA-LSSVM and PSO-LSSVM in terms of the RMSE, MAE, MAPE and R² evaluation criteria. For instance, the RMSE of CBEA-LSSVM is 1.3798, but the PSO-LSSVM and GA-LSSVM are 2.5701 and 2.8698, respectively. The coefficient of determination (R²) of CBEA-LSSVM is 0.9951, whereas those of the PSO-LSSVM and GA-LSSVM are 0.9883 and 0.9734, respectively.

The primary reason may be that CBEA does not have the binary code, crossover and mutation operations of the genetic algorithm, but CBEA can produce a new population by using the normal cloud generator and adaptively control the position, scope (the scope of searching), and agglomeration degree (the particle size of refinement) of offspring through using entropy and hyper-entropy, which equips the LSSVM model with excellent ability to obtain the optimal solution quickly and avoid the issue of premature local convergence. Moreover, compared with the genetic algorithm, when the difference of the fitness value of most of the individuals in the population seems slight, the crossover operation will be powerless, and the algorithm can be easy to fall into local solutions and cannot be solved through the exchange. The sudden mutation can get rid of local convergence and jump out the local solution, but later variation may damage the constructive module which is helpful to form the optimal solution. However, CBEA can effectively avoid the drawbacks of GA since the evolving variation and mutation both utilize the historical search results. Hence, CBEA is superior to the genetic algorithm in the process of parameter optimization. Furthermore, based on real coding, CBEA and PSO both do not have crossover and mutation. The PSO approach determines the search according to the speed of particle, and the particles follow the current optimal particle to search in the current solution space. However, CBEA is a process where the individual has been produced and eliminated in each evolving generation, which not only embodies the idea of evolution, but also reflects the characteristics of human searching. Therefore, CBEA performs better than PSO in the process of parameter optimization;

(2)

The improved LSSVM models outperform the single LSSVM approach using the grid searching method and cross validation approach. For instance, the MAPE of CBEA-LSSVM, PSO-LSSVM, and GA-LSSVM are 8.10%, 19.71%, and 26.98%, but the MAPE of the single LSSVM is 31.11%. A possible explanation may be that the improved LSSVM model endows the LSSVM with better learning and generalization ability to gain the global optimal strategy easily and efficiently;

(3)

When compared to the ARMA model using only its own historical data, the improved LSSVM models and BPNN are more effective than the ARMA model representing the statistical models for wind power generation prediction.

4.5.3. Paired-Sample t-test

Based on the principle of the comparison of the mean difference of paired observations, the paired-sample t-test [39] is applied to identify whether there is value to focus on the difference of forecasting results from the single LSSVM model and the hybrid LSSVM models for demonstrating the advantage of the hybrid LSSVM models further. The definition of hypothesis test is described as:

$$H_0:\overline{x_1}-\overline{x_2}=0,H_1:\overline{x_1}-\overline{x_2}\ne 0$$

(20)

where $\overline{x_1}$ represents the average prediction value with the single LSSVM method, $\overline{x_2}$ represents the average forecasting value with the hybrid models. In this test, if the probabilities of all pairs are lower than the significance level of 0.05, then the alternative hypothesis (H₁) is true for all pairs. Therefore, the null hypothesis (H₀) can be rejected.

Table 7. The results of paired-sample t-test.

Pairs	Paired Differences (Wind Power Generation Forecasted by Single LSSVM Model Minus Wind Power Generation Forecasted by Hybrid Model)				Probability (Two-Tailed)
	Mean	Standard Deviation	95% Confidence Interval of the Difference
			Lower	Upper
Pair 1: LSSVM–CBEA	−1.5119915	4.1382006	−2.4270228	−0.5969602	0.001
Pair 2: LSSVM–GA	−1.4031577	3.9581253	−2.2783711	−0.5279443	0.002
Pair 3: LSSVM–PSO	−1.4968162	4.0001929	−2.3813315	−0.6123010	0.001

gives the results of paired-sample t-test. As shown in Table 6, obviously the probabilities of all pairs are lower than the significance level of 0.05, indicating that the alternative hypothesis (H₁) is true and the null hypothesis (H₀) can be rejected. Therefore, it can be concluded that there exists the value to focus on the difference between $\overline{x_1}$ and $\overline{x_2}$ for all pairs, revealing that great changes occur using the parameter optimization of CBEA, GA and PSO.

5. Conclusions

This paper contributes to the development of an improved method of wind power generation prediction, refered to as the CBEA-LSSVM model. In order to enhance the forecasting accuracy, a two-way comparison approach is utilized to preprocess daily wind power generation series of a wind farm. The pertinent parameters of the proposed model are optimized by a CBEA. According to the simulation and the results analysis discussed in this paper, it can be concluded that: (1) the combination of CBEA and LSSVM can be an innovative practice for predicting the nonlinear wind power generation time series; (2) by selecting different initial parameters to explore the predictive performance of CBEA-LSSVM model, the simulation results indicate that the forecasting accuracy of the proposed model seems higher since the individual randomness with greater entropy may be larger; (3) based on the different evaluation criteria and the paired-sample t-test, CBEA-LSSVM performs better when compared to GA-LSSVM and PSO-LSSVM; (4) the prediction accuracy of the hybrid LSSVM models and the single LSSVM model precede the BPNN and ARMA approaches in wind power generation forecasting.

Although the proposed model has excellent performance in wind power generation forecasting, this study only selected the average wind speed as an exogenous variable of wind power generation. However, other relevant factors such as temperature, equivalent utilization hours, wind direction and availability of fan also can have great impacts on wind power generation, therefore, in future research we plan to incorporate the aforementioned factors and validate the developed method.