DG Mix and Energy Storage Units for Optimal Planning of Self-Sufficient Micro Energy Grids
Abstract
:1. Introduction
- ▪
- Electrical and heat demands with considering the hourly change during the day.
- ▪
- Economic objective (total capital, operational, and fuel costs) and environmental objective (CO2 emissions).
- ▪
- DG mix (natural gas turbines, natural gas fuel cells, and hydrogen gas fuel cells), renewable energy sources (wind and PV), natural gas boiler, electrical heater, and thermal/electrical storage.
2. Problem Description
3. Modeling of DG Units
3.1. Combined Heat and Power (CHP) Generators
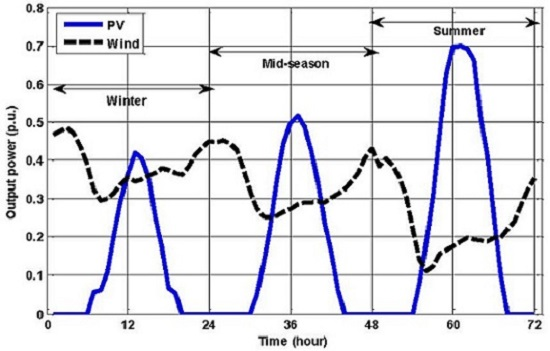
3.2. Renewable Energy Sources
- ▪
- Based on seasons, the entire year is divided into three seasons (winter, mid-season, and summer), and each season is being represented by one day, which is subdivided into 24-h segments.
- ▪
- The mean and standard deviation for each time segment are calculated utilizing the historical wind speed and solar irradiance data (i.e., three years of historical wind speed and solar irradiance data have been used).
- ▪
- Appropriate probability density functions (PDF) can be used to represent the behavior of the wind speed and solar irradiance during each hour of the day. Based on actual historical wind speed and solar irradiance data, Weibull and Beta probability density functions were used to model wind speed and solar irradiance respectively because they provide the best fit.
- ▪
- The Weibull and Beta probability density functions (PDFs) are generated for each hour using the mean and standard deviation for each segment.
- ▪
- In order to integrate the output power of wind- and PV-based generators in the formulation, the continuous PDF of each is divided into a proper number of states. Then the probability of each wind speed and solar irradiance state are calculated.
- ▪
- The corresponding output power of the wind turbine and PV module for each state are calculated using the wind turbine power performance curve and PV module characteristics.
- ▪
- For each time interval, the probability of each state can be multiplied by its output power and all of the resulting products can be totaled, thus enabling a determination of the expected value of the output power during that hour.
3.3. Energy Storage Systems
4. Problem Formulation
4.1. Objective (Fitness) Function
4.2. Constraints (Power and Heat Generation/Demand Balance Constraints)
4.3. Implementation of the Genetic Algorithm (GA)
4.4. Solution of the Bi-Objective Planning Problem
5. Case Study
- (1)
- Mode 1 “Following Electrical Load (FEL)” where DG units put the priority on electricity production to follow the required electrical demand. The deficient heat can be supplied by the thermal storage, boiler and/or electrical heater. The surplus heat can be stored in the thermal storage.
- (2)
- Mode 2 “Following Thermal Load (FTL)” where DG units put the priority on heat production to follow the required heat demand. The deficient electricity can be supplied by the electrical storage. The surplus electricity can be stored in the form of electricity in the electrical storage, or it can be converted to heat by the electrical heater to be stored in the thermal storage.
- Case 1:
- Planning problem for minimum cost (OF1 only is included).
- (1)
- Running cost only (i.e., operational cost and heat purchase from boiler)
- (2)
- Total running and capital costs
- Case 2:
- Planning problem for minimum emissions (OF2 only is included).
- Case 3:
- Planning problem for compromised solution with minimum possible cost and emissions (both OF1 and OF2 are included).
6. Results and Discussion
6.1. Results for Mode 1: Following Electrical Load (FEL)
6.1.1. Base Case Results
6.1.2. Results of Configuration 1 (CHPs)
6.1.3. Results of Configuration 2 (CHPs and Energy Storage)
6.1.4. Results of Configuration 3 (CHPs and Renewable Energy)
6.1.5. Results of Configuration 4 (CHPs, Energy Storage, and Renewable Energy)
6.2. Results for Mode 2: Following Thermal Load (FTL)
6.3. Islanded-Mode versus Grid-Connected Mode for Micro Energy Grids
- ▪
- Exchange of electrical energy with the main grid is possible during the grid-connected mode. A micro energy grid may increase its generation to maximize the revenue from selling surplus electricity to the main grid. Therefore, unrequired heat may be generated. However, there is no electricity exchange with the main grid during the islanded mode. This makes the amount of generated electricity and heat during the islanded mode is low compared to the grid-connected mode.
- ▪
- Due to high values of unrequired heat during grid-connected mode, thermal storage may be required with higher capacities compared to its value during the islanded mode.
- ▪
- The running cost, total cost, and greenhouse gas emissions during the islanded mode are low compared to the grid-connected mode for most case studies.
- ▪
- The generated heat by the natural gas-fired boiler during the islanded mode is lower compared to its generated value during the grid-connected mode.
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Bouffard, F.; Kirschen, D.S. Centralised and distributed electricity systems. Energy Policy 2008, 36, 4504–4508. [Google Scholar] [CrossRef]
- Zhang, D.; Evangelisti, S.; Lettieri, P.; Papageorgiou, L.G. Optimal design of CHP-based microgrids: Multiobjective optimisation and life cycle assessment. Energy 2015, 85, 181–193. [Google Scholar] [CrossRef]
- Rao, R.S.; Ravindra, K.; Satish, K.; Narasimham, S.V.L. Power loss minimization in distribution system using network reconfiguration in the presence of distributed generation. IEEE Trans. Power Syst. 2013, 28, 317–325. [Google Scholar] [CrossRef]
- Wu, X.; Wang, X.; Qu, C. A hierarchical framework for generation scheduling of microgrids. IEEE Trans. Power Deliv. 2014, 29, 2448–2457. [Google Scholar] [CrossRef]
- Conti, S.; Nicolosi, R.; Rizzo, S.A.; Zeineldin, H.H. Optimal dispatching of distributed generators and storage systems for MV islanded microgrids. IEEE Trans. Power Deliv. 2012, 27, 1243–1251. [Google Scholar] [CrossRef]
- Lund, H.; Andersen, A.N.; Østergaard, P.A.; Mathiesen, B.V.; Connolly, D. From electricity smart grids to smart energy systems—A market operation based approach and understanding. Energy 2012, 42, 96–102. [Google Scholar] [CrossRef]
- Xiao, J.; Bai, L.; Li, F.; Liang, H.; Wang, C. Sizing of energy storage and diesel generators in an isolated microgrid using Discrete Fourier Transform (DFT). IEEE Trans. Sustain. Energy 2014, 5, 907–916. [Google Scholar] [CrossRef]
- Andersen, A.N.; Lund, H. New CHP partnerships offering balancing of fluctuating renewable electricity productions. J. Clean. Prod. 2007, 15, 288–293. [Google Scholar] [CrossRef]
- Bin, W.; Ming, S.; Baole, D. The existed problems and possible solutions of distributed generation microgrid operation. In Proceedings of the 2011 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 25–28 March 2011; pp. 1–4.
- Khodaei, A. Microgrid optimal scheduling with multi-period islanding constraints. IEEE Trans. Power Syst. 2014, 29, 1383–1392. [Google Scholar] [CrossRef]
- Vafaei, M.; Kazerani, M. Optimal unit-sizing of a wind-hydrogen-diesel microgrid system for a remote community. In Proceedings of the IEEE Trondheim Power Tech, Trondheim, Norway, 19–23 June 2011; pp. 1–7.
- Chen, S.X.; Gooi, H.B.; Wang, M.Q. Sizing of energy storage for microgrids. IEEE Trans. Smart Grid 2012, 3, 142–151. [Google Scholar] [CrossRef]
- Khodaei, A.; Shahidehpour, M. Microgrid-based co-optimization of generation and transmission planning in power systems. IEEE Trans. Power Syst. 2013, 28, 1582–1590. [Google Scholar] [CrossRef]
- Buayai, K.; Ongsakul, W.; Mithulananthan, N. Multi-objective micro-grid planning by NSGA-II in primary distribution system. Eur. Trans. Electr. Power 2012, 22, 170–187. [Google Scholar] [CrossRef]
- Rigo-Mariani, R.; Sareni, B.; Roboam, X. Integrated optimal design of a smart microgrid with storage. IEEE Trans. Smart Grid 2015, PP, 1–9. [Google Scholar] [CrossRef]
- Atia, R.; Yamada, N. Sizing and analysis of renewable energy and battery systems in residential microgrids. IEEE Trans. Smart Grid 2016, 7, 1204–1213. [Google Scholar] [CrossRef]
- Zhang, J.; Li, K.J.; Wang, M.; Lee, W.J.; Gao, H.; Zhang, C.; Li, K. A bi-level program for the planning of an islanded microgrid including CAES. IEEE Trans. Ind. Appl. 2016, PP, 1–10. [Google Scholar] [CrossRef]
- Sachs, J.; Sawodny, O. Multi-objective three stage design optimization for island microgrids. Appli. Energy 2016, 165, 789–800. [Google Scholar] [CrossRef]
- Zidan, A.; Gabbar, H.A.; Eldessouky, A. Optimal planning of combined heat and power systems within microgrids. Energy 2015, 93, 235–244. [Google Scholar] [CrossRef]
- Abdelaziz, M.M.A.; Farag, H.E.; El-Saadany, E.F. Optimum reconfiguration of droop-controlled islanded microgrids. IEEE Trans. Power Syst. 2016, 31, 2144–2153. [Google Scholar] [CrossRef]
- Atwa, Y.M.; El-Saadany, E.F.; Salama, M.M.A.; Seethapathy, R. Optimal renewable resources mix for distribution system energy loss minimization. IEEE Trans. Power Syst. 2010, 25, 360–370. [Google Scholar] [CrossRef]
- Zidan, A.; El-Saadany, E.F. Incorporating load variation and variable wind generation in service restoration plans for distribution systems. Energy 2013, 57, 682–691. [Google Scholar] [CrossRef]
- Roberts, B. Capturing grid power. IEEE Power and Energy Mag. 2009, 7, 32–41. [Google Scholar] [CrossRef]
- Zidan, A.; El-Saadany, E.F. Incorporating customers’ reliability requirements and interruption characteristics in service restoration plans for distribution systems. Energy 2015, 87, 192–200. [Google Scholar] [CrossRef]
- Dzung, N.T. Application of multi-objective optimization by the utopian point method to determining the technological mode of gac oil extraction. Int. J. Chem. Eng. Appl. 2012, 3, 18–24. [Google Scholar] [CrossRef]
- Martínez, P.; Eliceche, A.M. Bi-objective minimization of environmental impact and cost in utility plants. Comput. Chem. Eng. 2011, 35, 1478–1487. [Google Scholar] [CrossRef]
- Hawkes, A.D.; Leach, M.A. Modelling high level system design and unit commitment for a microgrid. Appl. Energy 2009, 86, 1253–1265. [Google Scholar] [CrossRef]





| Configuration Number | CHP | Connection with the Main Grid | Energy Storage | Renewable Energy | ||||
|---|---|---|---|---|---|---|---|---|
| NGT | H2FC | NGFC | Thermal | Electrical | Wind | PV | ||
| 1 | √ | √ | √ | |||||
| 2 | √ | √ | √ | √ | √ | |||
| 3 | √ | √ | √ | √ | √ | |||
| 4 | √ | √ | √ | √ | √ | √ | √ | |
| Base | √ | |||||||
| Config. Number | Case | Cost ($) | Total CO2 Emission (kg) | DGs Generated Energy | Generated Heat (MWh) | Rated Size (kW) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Running | Total | Electricity (MWh) | Heat (MWh) | Boiler | Electrical Heater | TS | NGT | H2FC | NGFC | WT | PV | TS | ES | |||||
| DGs | ES | |||||||||||||||||
| 1 | 1 | a | 7.63 × 104 | 3.23 × 105 | 4.05 × 105 | 9638.2 | 0 | 12,503.6 | 0 | 2605.3 | 0 | 3228.8 | 0 | 0 | 0 | 0 | 0 | 0 |
| b | 1.02 × 105 | 3.19 × 105 | 8.07 × 105 | 9260.8 | 0 | 12,014.1 | 866.9 | 2227.9 | 0 | 2845.0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 2 | 1.79 × 106 | 3.47 × 106 | 0 | 9768.7 | 0 | 12,210.9 | 0 | 2735.8 | 0 | 0 | 3296.7 | 0 | 0 | 0 | 0 | 0 | ||
| 3 | 9.86 × 104 | 3.63 × 105 | 4.00 × 105 | 9639.9 | 0 | 12,499.8 | 0 | 2607.0 | 0 | 3187.0 | 42.5 | 0 | 0 | 0 | 0 | 0 | ||
| 2 | 1 | a | 7.44 × 104 | 3.19 × 105 | 3.82 × 105 | 9100.7 | 0 | 11,806.3 | 0 | 2067.8 | 905.8 | 3066.9 | 0 | 0 | 0 | 0 | 3454.5 | 0 |
| b | 7.45 × 104 | 2.53 × 105 | 3.83 × 105 | 9021.0 | 0 | 11,344.1 | 0 | 1988.1 | 985.1 | 2201.2 | 0 | 0 | 0 | 0 | 3454.5 | 0 | ||
| 2 | 1.71 × 106 | 3.40 × 106 | 0 | 9283.8 | 0 | 11,604.7 | 0 | 2250.9 | 1238.9 | 0 | 3296.6 | 0 | 0 | 0 | 4074.1 | 0 | ||
| 3 | 7.44 × 104 | 3.32 × 105 | 3.82×105 | 9102.0 | 0 | 11,806.5 | 0 | 2069.1 | 1234.8 | 3228.8 | 0 | 0 | 0 | 0 | 3454.5 | 0 | ||
| 3 | 1 | a | 7.83 × 104 | 3.56 × 105 | 3.89 × 105 | 9760.2 | 0 | 11,998.6 | 0 | 2727.3 | 0 | 3193.2 | 0 | 0 | 179 | 0 | 0 | 0 |
| b | 1.58 × 105 | 3.26 × 105 | 1.67 × 106 | 8446.4 | 0 | 10,948.4 | 2743.9 | 1413.5 | 0 | 2178.3 | 0 | 0 | 2 | 0 | 0 | 0 | ||
| 2 | 1.68 × 106 | 3.63 × 106 | 0 | 10,044.0 | 0 | 11,332.2 | 0 | 3011.1 | 0 | 0 | 3296.7 | 0 | 0 | 670 | 0 | 0 | ||
| 3 | 8.06 × 104 | 4.75 × 105 | 3.69 × 105 | 9896.2 | 0 | 11,395.5 | 0 | 2863.3 | 0 | 3176.6 | 0 | 0 | 262 | 250 | 0 | 0 | ||
| 4 | 1 | a | 7.68 × 104 | 3.87 × 105 | 3.73 × 105 | 9304.6 | 0 | 11,522.2 | 0 | 2271.7 | 1151.4 | 3207.7 | 0 | 0 | 106 | 82 | 3855.3 | 0 |
| b | 8.80 × 104 | 3.37 × 105 | 5.77 × 105 | 8977.7 | 0 | 11,471.0 | 426.9 | 1944.8 | 1196.5 | 2988.0 | 0 | 0 | 43 | 8 | 3294.5 | 0 | ||
| 2 | 1.42 × 106 | 3.81 × 106 | 0 | 10,578.1 | 0 | 9452.6 | 0 | 3545.2 | 702.1 | 0 | 3249.3 | 0 | 233 | 1677 | 1650.8 | 0 | ||
| 3 | 7.51 × 104 | 3.31 × 105 | 3.92 × 105 | 9096.2 | 0 | 11,787.7 | 20.8 | 2063.3 | 1231.8 | 3216.6 | 0 | 0 | 3 | 0 | 3443.7 | 0 | ||
| Base * | 7.74 × 105 | 7.74 × 105 | 6.93 × 106 | 0 | 0 | 0 | 11,474.70 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Config. Number | Case | Cost ($) | Total CO2 Emission (kg) | DGs Generated Energy | Generated Heat (MWh) | Rated Size (kW) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Running | Total | Electricity (MWh) | Heat (MWh) | Boiler | Electrical Heater | TS | NGT | H2FC | NGFC | WT | PV | TS | ES | |||||
| DGs | ES | |||||||||||||||||
| 4 | 1 | a | 6.72 × 104 | 4.58 × 105 | 3.18 × 105 | 9300.9 | 372.8 | 9828.0 | 0 | 1646.7 | 0 | 3369.2 | 0 | 0 | 243.0 | 0 | 0 | 659.8 |
| b | 6.93 × 104 | 4.29 × 105 | 3.11 × 105 | 9557.1 | 401.9 | 9620.3 | 0 | 1854.4 | 0 | 3254.3 | 0 | 0 | 267.0 | 45.3 | 0 | 314.4 | ||
| 2 | 1.38 × 106 | 3.44 × 106 | 0 | 11,244.5 | 1146.9 | 9174.6 | 0 | 2300.1 | 0 | 0 | 3357.8 | 0 | 510.8 | 116.8 | 0 | 1532.6 | ||
| 3 | 6.87 × 104 | 4.65 × 105 | 3.17 × 105 | 9188.4 | 279.1 | 9784.4 | 0 | 1690.3 | 0 | 3356.4 | 0 | 0 | 262.5 | 0 | 0 | 681.2 | ||
| Config. | Mode | Minimum Cost Solution | Minimum Emission Solution | Compromised Solution | |||
|---|---|---|---|---|---|---|---|
| Total Cost (105 $) | Total CO2 Emissions (105 kg) | Total Cost (106 $) | Total CO2 Emissions (105 kg) | Total Cost (105 $) | Total CO2 Emissions (105 kg) | ||
| 1 | Gird-connected [19] | 4.03 | 32.2 | 2.44 | 9.36 | 5.61 | 11.8 |
| Islanded | 3.19 | 8.07 | 3.47 | 0 | 3.63 | 4.00 | |
| 2 | Gird-connected [19] | 3.75 | 26.4 | 2.13 | 7.92 | 4.99 | 9.99 |
| Islanded | 2.53 | 3.83 | 3.40 | 0 | 3.32 | 3.82 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zidan, A.; Gabbar, H.A. DG Mix and Energy Storage Units for Optimal Planning of Self-Sufficient Micro Energy Grids. Energies 2016, 9, 616. https://doi.org/10.3390/en9080616
Zidan A, Gabbar HA. DG Mix and Energy Storage Units for Optimal Planning of Self-Sufficient Micro Energy Grids. Energies. 2016; 9(8):616. https://doi.org/10.3390/en9080616
Chicago/Turabian StyleZidan, Aboelsood, and Hossam A. Gabbar. 2016. "DG Mix and Energy Storage Units for Optimal Planning of Self-Sufficient Micro Energy Grids" Energies 9, no. 8: 616. https://doi.org/10.3390/en9080616
APA StyleZidan, A., & Gabbar, H. A. (2016). DG Mix and Energy Storage Units for Optimal Planning of Self-Sufficient Micro Energy Grids. Energies, 9(8), 616. https://doi.org/10.3390/en9080616