Some Models for Determination of Parameters of the Soil Oscillation Law during Blasting Operations
Abstract
:1. Introduction
2. Soil Oscillation Law
- v—velocity of soil oscillation (m/s);
- K—coefficient conditioned by soil characteristics, as well as blasting conditions, where the explosive amount is given by way of the volume. K is being determined by terrain surveying;
- n—exponent, conditioned by soil properties and mining conditions and determined by field measurements as well;
- r—distance from the blast site to the monitoring point (m);
- Q—amount of explosive (kg); and
- R—reduced distance, expressed as .
2.1. Derivation of Equation of Rock Mass Oscillation Law
2.1.1. Derivation of Equation of Rock Mass Oscillation—First Mode
- v—velocity of soil oscillation (cm/s);
- Kv—coefficient conditioned by soil characteristics, as well as blasting conditions, where the explosive amount is given through radius of the explosive charge. Kv is being determined by terrain surveying;
- r—distance from the blast site to the monitoring point (m);
- r0—radius of the explosive charge; and
- n—exponent, conditioned by soil properties and mining conditions and determined by field measurements as well.
- R—reduced distance is the distance from blasting point to observation point reduced to a quantity of explosive and given in the following form: .
2.1.2. Derivation of Equation of Rock Mass Oscillation—Second Mode
- R—distance from the blast site to the monitoring point (m); and
- Q—overall amount of explosive in a mine series (kg).
2.2. Models of Determination of Soil Oscillation Law Parameters
2.2.1. Model 1—Determining the Parameters by Applying the Least Square Method
2.2.2. Model 2—Determining the Parameters by Applying the Quotient of the Relative Growth of Oscillation Velocities and Reduced Distances
2.2.3. Model 3—Determining the Parameters between Parameters K and n is Determined by Applying the Trapezoidal Formula for Finding the Value of Definite Integral
- Sm—surfaces of some trapezoids.
3. Defining Statistical Criteria
- 0.0 < ρ < 0.2—none or highly poor correlation;
- 0.2 < ρ < 0.4—poor correlation;
- 0.4 < ρ < 0.7—significant correlation; and
- 0.7 < ρ < 1.0—strong or highly strong correlation.
- if |εmax| ≥ 3S, the obtained functional correlation is rejected as unfavorable; and
- if |εmax| < 3S, the functional correlation is accepted as a good one.
4. Methodology of Research
- experimental investigations performed in the Veliki Krivelj Open Pit in the Bor District, and
- investigation carried out during mass mining in the Kovilovača Open Pit near Despotovac.
4.1. Experimental Investigation in the VelikiKrivelj Open Pit
4.1.1. General Characteristics of the Work Environment in the Veliki Krivelj Open Pit
- compressive strength, σp = 31 MPa;
- bending strength, σs = 5.1 MPa;
- tensile strength, σI = 3.4 MPa;
- cohesion, C = 7.5 MPa;
- strength coefficient, f = 3;
- volume density, γ = 24 kN/m3;
- angle of internal friction, ϕ = 52°;
- porosity, p = 3.5%;
- velocity of longitudinal waves, cp = 2400.00 m/s;
- velocity of transverse waves, cs = 1400.00 m/s.
4.1.2. Method of Blasting in the Veliki Krivelj Open Pit
- depth of borehole: 0.5 m;
- weight of explosive charge per borehole: 0.10 kg;
- number of boreholes: 10;
- distance between boreholes: 1.0 m;
- distance between measuring point and the first borehole: 5.0 m; and
- delay time between initiation of boreholes: 0.5 s.
4.1.3. Calculation for Parameters of the Soil Oscillation Law in the Veliki Krivelj Open Pit
- Model 1
- Model 2
- Model 3
- R1 = 10.7722; RN = R10 = 30.1621; Ri+1 − Ri = h = 2.1544,
- ST = 12.9953
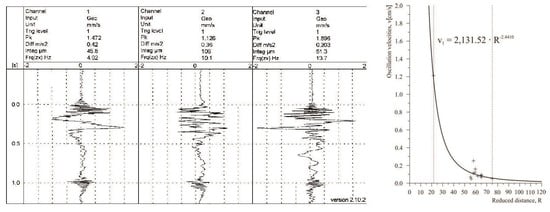
- For model 1:The curved line dependency index ρ1 between the reduced distance R and soil oscillation velocity v is:
- ρ1 = 0.9880 (there is a strong correlation between R and v, given in Equation (28)).
The maximum difference between the recorded and calculated oscillation velocities of the soil, (εmax) = max |εi|, amounts:- εmax1 = 0.1204, S1 = 0.0592, 3S1 = 0.1776.
- As εmax1 < 3S1, the supposed functional relationship is accepted as a good one.
- For model 2:
- ρ2 = 0.9893 (there is a strong correlation between R and v, given in Equation (29)).
- εmax2 = 0.1147, S2 = 0.0550, 3S2 = 0.1650.
- εmax2 < 3S2 (the supposed functional relationship is accepted as a good one).
- For model 3:
- ρ3 = 0.9887 (there is a strong correlation between R and v, given in Equation (30)).
- εmax3 = 0.1089, S3 = 0.0566, 3S3 = 0.1698.
- εmax3 < 3S3 (supposed functional relationship is accepted as a good one).
4.2. Investigation during Mass Mining in the Kovilovača Open Pit
4.2.1. General Characteristics of the Kovilovača Open Pit
- angle of internal friction: φ = 31°35′
- cohesion: C = 138.33 kPa
- volume weight: γ = 26.26 kN/m3
- compressive strength: σp = 80.808 MPa
- tensile strength: σz = 7.59 MPa
- velocity of longitudinal elastic waves: cp = 6661.00 m/s
- velocity of transverse elastic waves: cs = 2852.67 m/s
- dynamic elasticity modulus: Edin = 62.46 GPa
- dynamic Poisson’s ratio: μdin = 0.39 GPa
4.2.2. Method of Blasting in the Kovilovača Open Pit
4.2.3. Calculation of Soil Oscillation Law Parameters in the Kovilovača Open Pit
- Model 1
- Model 2
- Model 3By using experimental data given in Table 4, where:
- R1 = 21.8117, RN = R12 = 75.2014,
- ST = 22.9538,
- For model 1The curved line dependency index ρ1 between the reduced distance R and soil oscillation velocity v is:
- ρ1 = 0.9843 (there is a strong correlation between R an v, given in Equation (31)).
The maximum difference between the recorded and calculated oscillation velocities of the soil (εmax) = max|εi|, amounts:- εmax1 = 0.1458, S1 = 0.0552, 3S1 = 0.1656.
- εmax1< 3S1, the (the supposed functional relationship is accepted as a good one).
- For model 2:
- ρ2 = 0.9852 (there is a strong correlation between R and v, given in Equation (32)).
- εmax2 = 0.1541, S2 = 0.0535, 3S2 = 0.1606.
- εmax2 < 3S2 (the supposed functional relationship is accepted as a good one).
- For model 3:
- ρ3 = 0.8768 (there is a strong correlation between R and v, given in Equation (33)).
- εmax3 = 0.2300, S3 = 0.1503, 3S3 = 0.4509.
- εmax3 < 3S3 (the supposed functional relationship is accepted as a good one).
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Savić, M. Blasting at of the Open Pits; Monograph, RTB Bor; Cooper Institute Bor, Indok Center: Bor, Serbia, 2000; pp. 317–319. [Google Scholar]
- Trajković, S.; Slimak, Š.; Lutovac, S. Technique of Blasting and Shock Waves; Faculty of Mining and Geology: Belgrade, Serbia, 2005; p. 199. [Google Scholar]
- Medvedev, S.V. Seismic of Mountainous Explosions; Nedra Publisher: Moscow, Russia, 1964; pp. 42–43. [Google Scholar]
- Lutovac, S.; Gligorić, Z.; Beljić, Č.; Ravilić, M. Derivation the soil oscillation law and determination of its parameters. Min. Metall. Eng. Bor 2014, 3, 41–51. [Google Scholar] [CrossRef]
- Simeunović, D. Mathematics; Faculty of Mining and Geology, Mining Department: Belgrade, Serbia, 1985; pp. 101–103. [Google Scholar]
- Lutovac, S.; Trajković, S.; Katona, O.; Savić, L.J.; Leković, B. Parameter determination of soil oscillation in limestone. Tech. Technol. Educ. Manag. (DRUNPP Sarajevo) 2013, 7, 376–383. [Google Scholar]
- Lutovac, S. Model for Determining the Parameters of the Law of Oscillation of the Rock Mass in Blasting. Ph.D. Thesis, Faculty of Mining and Geology, University of Belgrade, Belgrade, Serbia, 2010; pp. 37–38, 48–55. [Google Scholar]
- Kudryavtsev, V.A.; Demidovich, B.P. A Brief Course of Higher Mathematics, 2nd ed.; Mir Publishers: Moscow, Russia, 1984; pp. 293–295. [Google Scholar]
- Petrović, Ž. Business Statistics, Megatrend; University of Applied Sciences: Belgrade, Serbia; Faculty for Management: Zaječar, Serbia, 2004; p. 182. [Google Scholar]
- Vukadinović, S. Elementsof Probability and Mathematical Statistics; Technique for Copying Bureau of Construction: Belgrade, Serbia, 1970; pp. 329–331. [Google Scholar]
- Trajković, S.; Tokalić, R.; Lutovac, S. Study of Seismic Impacts on Adjacent Building due to Blasting Operations at Kovilovača Open Pit; Faculty of Mining and Geology: Belgrade, Serbia, 2004; pp. 2–43. [Google Scholar]






| No. | Blasting | r (m) | Q (kg) | R | vt (cm/s) | vv (cm/s) | vl (cm/s) | vrez (cm/s) |
|---|---|---|---|---|---|---|---|---|
| 1 | I | 5.0 | 0.1 | 10.7722 | 0.4200 | 0.9300 | 1.1400 | 1.5300 |
| 2 | I | 6.0 | 0.1 | 12.9266 | 0.3000 | 0.6000 | 1.0500 | 1.2460 |
| 3 | I | 7.0 | 0.1 | 15.0810 | 0.2400 | 0.4000 | 0.6450 | 0.7960 |
| 4 | I | 8. 0 | 0.1 | 17.2355 | 0.2000 | 0.3750 | 0.5000 | 0.6562 |
| 5 | I | 9.0 | 0.1 | 19.3899 | 0.1800 | 0.4000 | 0.4750 | 0.6465 |
| 6 | I | 10.0 | 0.1 | 21.5443 | 0.1500 | 0.3000 | 0.4000 | 0.5220 |
| 7 | I | 11.0 | 0.1 | 23.6988 | 0.1900 | 0.2700 | 0.3300 | 0.4668 |
| 8 | I | 12.0 | 0.1 | 25.8532 | 0.1900 | 0.2100 | 0.2900 | 0.4053 |
| 9 | I | 13.0 | 0.1 | 28.0077 | 0.1500 | 0.2150 | 0.2500 | 0.3622 |
| 10 | I | 14.0 | 0.1 | 30.1621 | 0.1400 | 0.2250 | 0.2000 | 0.3320 |
| No. | R | vr (cm/s) | vi1 (cm/s) | vi2 (cm/s) | vi3 (cm/s) | vr − vi1 | vr − vi2 | vr − vi3 |
|---|---|---|---|---|---|---|---|---|
| 1 | 10.7722 | 1.5300 | 1.4737 | 1.5300 | 1.4990 | 0.0563 | 0.0000 | 0.0310 |
| 2 | 12.9266 | 1.2460 | 1.1256 | 1.1551 | 1.1404 | 0.1204 | 0.0909 | 0.1056 |
| 3 | 15.0810 | 0.7960 | 0.8962 | 0.9107 | 0.9049 | −0.1002 | −0.1147 | −0.1089 |
| 4 | 17.2355 | 0.6562 | 0.7357 | 0.7412 | 0.7407 | −0.0795 | −0.0850 | −0.0845 |
| 5 | 19.3899 | 0.6465 | 0.6182 | 0.6181 | 0.6207 | 0.0283 | 0.0284 | 0.0258 |
| 6 | 21.5443 | 0.5220 | 0.5290 | 0.5255 | 0.5300 | −0.0070 | −0.0035 | −0.0080 |
| 7 | 23.6988 | 0.4668 | 0.4595 | 0.4536 | 0.4594 | 0.0073 | 0.0132 | 0.0074 |
| 8 | 25.8532 | 0.4053 | 0.4041 | 0.3967 | 0.4032 | 0.0012 | 0.0086 | 0.0024 |
| 9 | 28.0077 | 0.3622 | 0.3590 | 0.3506 | 0.3576 | 0.0032 | 0.0116 | 0.0046 |
| 10 | 30.1621 | 0.3320 | 0.3217 | 0.3128 | 0.3199 | 0.0103 | 0.0192 | 0.0121 |
| Blasting | Nb | Quk (kg) | Qi (kg) | Luk (m) | Lpč (m) |
|---|---|---|---|---|---|
| I | 34 | 3623.0 | 108.0 | 842.0 | 2.2 |
| II | 36 | 3264.0 | 92.0 | 918.0 | 2.2 |
| No. | MM | r (m) | Q (kg) | R | vt (cm/s) | vv (cm/s) | vl (cm/s) | vrez (cm/s) |
|---|---|---|---|---|---|---|---|---|
| 1 | MM–1 | 335.0 | 3.623.0 | 21.8117 | 0.1460 | 0.0517 | 1.2000 | 1.2100 |
| 2 | MM–3 | 850.0 | 3.623.0 | 55.3430 | 0.0138 | 0.0270 | 0.0617 | 0.0687 |
| 3 | MM–5 | 830.0 | 3.264.0 | 55.9536 | 0.0206 | 0.0133 | 0.0407 | 0.0475 |
| 4 | MM–9 | 855.0 | 3.264.0 | 57.6390 | 0.0200 | 0.1070 | 0.0245 | 0.1116 |
| 5 | MM–3 | 860.0 | 3.264.0 | 57.9760 | 0.1400 | 0.1010 | 0.1830 | 0.2516 |
| 6 | MM–10 | 880.0 | 3.264.0 | 59.3234 | 0.0729 | 0.0936 | 0.0156 | 0.1197 |
| 7 | MM–10a | 885.0 | 3.264.0 | 59.6614 | 0.0134 | 0.1530 | 0.0426 | 0.1594 |
| 8 | MM–7 | 950.0 | 3.623.0 | 61.8540 | 0.0222 | 0.0422 | 0.0623 | 0.0785 |
| 9 | MM–7 | 960.0 | 3.264.0 | 64.7174 | 0.0174 | 0.0477 | 0.0708 | 0.0871 |
| 10 | MM–6 | 965.0 | 3.264.0 | 65.0545 | 0.0045 | 0.0337 | 0.0555 | 0.0651 |
| 11 | MM–6a | 970.0 | 3.264.0 | 65.3916 | 0.0202 | 0.0568 | 0.0711 | 0.0932 |
| 12 | MM–8 | 1,155.0 | 3.623.0 | 75.2014 | 0.0327 | 0.0317 | 0.0246 | 0.0518 |
| No. | R | vr (cm/s) | vi1 (cm/s) | vi2 (cm/s) | vi3 (cm/s) | vr − vi1 | vr − vi2 | vr − vi3 |
|---|---|---|---|---|---|---|---|---|
| 1 | 21.8117 | 1.2100 | 1.1507 | 1.2100 | 1.1403 | 0.0593 | 0.0000 | 0.0697 |
| 2 | 55.3430 | 0.0687 | 0.1185 | 0.1196 | 0.2821 | −0.0498 | −0.0509 | −0.2134 |
| 3 | 55.9536 | 0.0475 | 0.1154 | 0.1164 | 0.2775 | −0.0679 | −0.0689 | −0.2300 |
| 4 | 57.6390 | 0.1116 | 0.1073 | 0.1081 | 0.2654 | 0.0043 | 0.0035 | −0.1538 |
| 5 | 57.9760 | 0.2516 | 0.1058 | 0.1065 | 0.2631 | 0.1458 | 0.1451 | −0.0115 |
| 6 | 59.3234 | 0.1197 | 0.1001 | 0.1006 | 0.2542 | 0.0196 | 0.0191 | −0.1345 |
| 7 | 59.6614 | 0.1594 | 0.0987 | 0.0992 | 0.2521 | 0.0607 | 0.0602 | −0.0927 |
| 8 | 61.8540 | 0.0785 | 0.0904 | 0.0907 | 0.2388 | −0.0119 | −0.0122 | −0.1603 |
| 9 | 64.7174 | 0.0871 | 0.0809 | 0.0811 | 0.2231 | 0.0062 | 0.0060 | −0.1360 |
| 10 | 65.0545 | 0.0651 | 0.0799 | 0.0800 | 0.2214 | −0.0148 | −0.0149 | −0.1563 |
| 11 | 65.3916 | 0.0932 | 0.0789 | 0.0790 | 0.2197 | 0.0143 | 0.0142 | −0.1805 |
| 12 | 75.2014 | 0.0518 | 0.0561 | 0.0558 | 0.1781 | −0.0043 | −0.0040 | −0.1263 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lutovac, S.; Medenica, D.; Gluščević, B.; Tokalić, R.; Beljić, Č. Some Models for Determination of Parameters of the Soil Oscillation Law during Blasting Operations. Energies 2016, 9, 617. https://doi.org/10.3390/en9080617
Lutovac S, Medenica D, Gluščević B, Tokalić R, Beljić Č. Some Models for Determination of Parameters of the Soil Oscillation Law during Blasting Operations. Energies. 2016; 9(8):617. https://doi.org/10.3390/en9080617
Chicago/Turabian StyleLutovac, Suzana, Dragan Medenica, Branko Gluščević, Rade Tokalić, and Čedomir Beljić. 2016. "Some Models for Determination of Parameters of the Soil Oscillation Law during Blasting Operations" Energies 9, no. 8: 617. https://doi.org/10.3390/en9080617
APA StyleLutovac, S., Medenica, D., Gluščević, B., Tokalić, R., & Beljić, Č. (2016). Some Models for Determination of Parameters of the Soil Oscillation Law during Blasting Operations. Energies, 9(8), 617. https://doi.org/10.3390/en9080617