A Concentrator Photovoltaic System Based on a Combination of Prism-Compound Parabolic Concentrators
Abstract
:1. Introduction
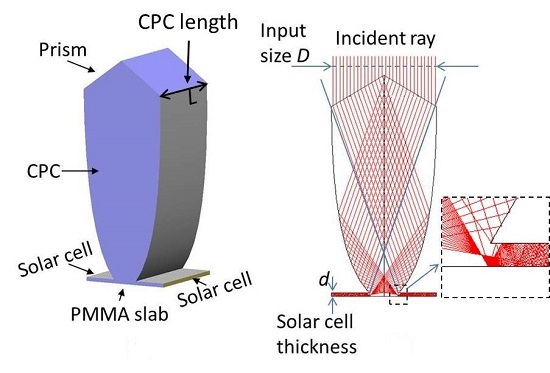
2. Proposed Sunlight Concentrator of CPV System
3. Optical Analysis and Performance
3.1. Optimization of the Shape of the CPC
3.2. The Dependence of Efficiency on the System Concentration Ratio CR
3.3. Tolerance of the System
3.4. Irradiance Distribution on the Surface of the Solar Cell
3.5. Proposed Large-Scale System and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Baig, H.; Sellami, N.; Mallick, T.K. Trapping Light Escaping from the Edges of the Optical Element in a Concentrating Photovoltaic System. Energy Convers. Manag. 2015, 90, 238–246. [Google Scholar] [CrossRef]
- Rumyantsev, V.D.; Ashcheulov, Y.V.; Davidyuk, N.Y.; Ionova, E.A.; Pokrovskiy, P.V.; Sadchikov, N.A.; Andreev, V.M. CPV Modules Based on Lens Panels. Adv. Sci. Technol. 2010, 74, 211–218. [Google Scholar] [CrossRef]
- Rumyantsev, V.D. Solar concentrator modules with silicone-onglass Fresnel lens panels and multijunction cells. Opt. Express 2010, 18, A17–A24. [Google Scholar] [CrossRef] [PubMed]
- Pei, G.; Li, G.; Su, Y.; Ji, J.; Riffat, S.; Zheng, H. Preliminary ray tracing and experimental study on the effect of mirror coating on the optical efficiency of a solid dielectric compound parabolic concentrator. Energies 2012, 5, 3627–3639. [Google Scholar] [CrossRef]
- Antonini, A.; Stefancich, M.; Coventry, J.; Parretta, A. Modelling of Compound Parabolic Concentrators for Photovoltaic Applications. Int. J. Opt. Appl. 2013, 3, 40–52. [Google Scholar] [CrossRef]
- Jing, L.; Liu, H.; Wang, Y.; Xu, W.; Zhang, H.; Lu, Z. Design and optimization of fresnel lens for high concentration photovoltaic system. Int. J. Photoenergy 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Benítez, P.; Miñano, J.C.; Zamora, P.; Mohedano, R.; Cvetkovic, A.; Buljan, M.; Chaves, J.; Hernández, M. High performance Fresnel-based photovoltaic concentrator. Opt. Express 2010, 18, A25–A40. [Google Scholar] [CrossRef] [PubMed]
- Winston, R. Principles of Solar Concentrators of a Novel Design. Sol. Energy 1974, 16, 89–95. [Google Scholar] [CrossRef]
- Parretta, A.; Antonini, A. Optics of Solar Concentrators. Part II: Models of Light Collection of 3D-CPCs under Direct and Collimated Beams. Int. J. Opt. Appl. 2013, 3, 72–102. [Google Scholar]
- Winston, R. Dielectric compound parabolic concentrators. Appl. Opt. 1976, 15, 291–292. [Google Scholar] [CrossRef] [PubMed]
- Mallick, T.K.; Eames, P.C.; Norton, B. Non-concentrating and asymmetric compound parabolic concentrating building facade integrated photovoltaics: An experimental comparison. Sol. Energy 2006, 80, 834–849. [Google Scholar] [CrossRef]
- Rabl, A. Comparison of solar concentrators. Sol. Energy 1976, 18, 93–111. [Google Scholar] [CrossRef]
- Goodman, N.B.; Ignatius, R.; Wharton, L.; Winston, R. Solid-dielectric compound parabolic concentrators: On their use with photovoltaic devices. Appl. Opt. 1976, 15, 2434–2436. [Google Scholar] [CrossRef] [PubMed]
- Winston, R.; Zhang, W. Pushing concentration of stationary solar concentrators to the limit. Opt. Express 2010, 18, A64–A72. [Google Scholar] [CrossRef] [PubMed]
- Tsuei, C.-H.; Sun, W.-S.; Kuo, C.-C. Hybrid sunlight/LED illumination and renewable solar energy saving concepts for indoor lighting. Opt. Express 2010, 18, A640–A653. [Google Scholar] [CrossRef] [PubMed]
- Gajic, M.; Karwa, M.; Mojiri, A.; Rosengarten, G. Modeling reflection loss from an evacuated tube inside a compound parabolic concentrator with a cylindrical receiver. Opt. Express 2015, 23, A493–A501. [Google Scholar] [CrossRef] [PubMed]
- Gueymard, C.A.; Myers, D.; Emery, K. Proposed reference irradiance spectra for solar energy systems testing. Sol. Energy 2002, 73, 443–467. [Google Scholar] [CrossRef]
- Lee, C.; Chou, P.; Chiang, C.; Lin, C. Sun tracking systems: A review. Sensors 2009, 9, 3875–3890. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.T.A.; Tanzil, S.M.S.; Rahman, R.; Alam, S.M.S. Design and construction of an automatic solar tracking system. In Proceedings of the 2010 International Conference on Electrical and Computer Engineering (ICECE), Dhaka, Bangladesh, 18–20 December 2010; pp. 326–329.
- Song, J.; Zhu, Y.; Jin, Z.; Yang, Y. Daylighting system via fibers based on two-stage sun-tracking model. Sol. Energy 2014, 108, 331–339. [Google Scholar] [CrossRef]
- Mousazadeh, H.; Keyhani, A.; Javadi, A.; Mobli, H.; Abrinia, K.; Sharifi, A. A review of principle and sun-tracking methods for maximizing solar systems output. Renew. Sustain. Energy Rev. 2009, 13, 1800–1818. [Google Scholar] [CrossRef]
- Xie, P.; Lin, H.; Liu, Y.; Li, B. Total internal reflection-based planar waveguide solar concentrator with symmetric air prisms as couplers. Opt. Express 2014, 22. [Google Scholar] [CrossRef] [PubMed]
- Bouchard, S.; Thibault, S. Planar waveguide concentrator used with a seasonal tracker. Appl. Opt. 2012, 51. [Google Scholar] [CrossRef] [PubMed]
- Moore, D.; Schmidt, G.; Unger, B. Concentrated photovoltaics stepped planar light guide. In Proceedings of the International Optical Design Conference 2010, Jackson Hole, WY, USA, 13–17 June 2010; Volume 7652. [CrossRef]
- Selimoglu, O.; Turan, R. Exploration of the horizontally staggered light guides for high concentration CPV applications. Opt. Express 2012, 20, 19137–19147. [Google Scholar] [CrossRef] [PubMed]
- Shen, S.C.; Chang, S.J.; Yeh, C.Y.; Teng, P.C. Design and testing of a uniformly solar energy TIR-R concentration lenses for HCPV systems. Opt. Express 2013, 21, A942–A952. [Google Scholar] [CrossRef] [PubMed]
- Ullah, I.; Shin, S. Highly concentrated optical fiber-based daylighting systems for multi-floor office buildings. Energy Build. 2014, 72, 246–261. [Google Scholar] [CrossRef]
- O’Driscoll, M. Design for manufacture. J. Mater. Process. Technol. 2002, 122, 318–321. [Google Scholar] [CrossRef]















© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, N.H.; Shin, S. A Concentrator Photovoltaic System Based on a Combination of Prism-Compound Parabolic Concentrators. Energies 2016, 9, 645. https://doi.org/10.3390/en9080645
Vu NH, Shin S. A Concentrator Photovoltaic System Based on a Combination of Prism-Compound Parabolic Concentrators. Energies. 2016; 9(8):645. https://doi.org/10.3390/en9080645
Chicago/Turabian StyleVu, Ngoc Hai, and Seoyong Shin. 2016. "A Concentrator Photovoltaic System Based on a Combination of Prism-Compound Parabolic Concentrators" Energies 9, no. 8: 645. https://doi.org/10.3390/en9080645
APA StyleVu, N. H., & Shin, S. (2016). A Concentrator Photovoltaic System Based on a Combination of Prism-Compound Parabolic Concentrators. Energies, 9(8), 645. https://doi.org/10.3390/en9080645