Optical Design of Textured Thin-Film CIGS Solar Cells with Nearly-Invisible Nanowire Assisted Front Contacts
Abstract
:1. Introduction
2. Results
2.1. Spectra of Whole Stack
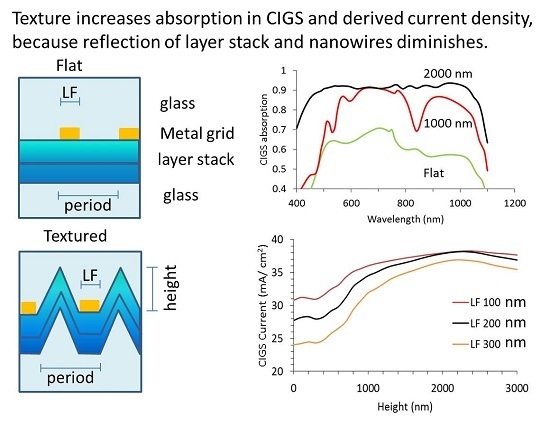
2.2. Trends of CIGS and Reflection Spectra
2.3. Current Densities of CIGS and Optical Loss
3. Methods
4. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Brecl, K.; Topič, M. Simulation of losses in thin-film silicon modules for different configurations and front contacts. Prog. Photovolt. Res. Appl. 2008, 16, 479–488. [Google Scholar] [CrossRef]
- Keller, J.; Lindahl, J.; Edoff, M.; Stolt, L.; Törndahl, T. Potential gain in photocurrent generation for Cu(In,Ga)Se2 solar cells by using In2O3 as a transparent conductive oxide layer. Prog. Photovolt. Res. Appl. 2016, 24, 102–107. [Google Scholar] [CrossRef]
- Van Deelen, J.; Tezsevin, Y.; Barink, M. Multi-material front contact for 19% thin film solar cells. Materials 2016, 9, 96. [Google Scholar] [CrossRef]
- Blakers, A.W. Shading losses of solar-cell metal grids. J. Appl. Phys. 1992, 71, 5237–5241. [Google Scholar] [CrossRef]
- Van Deelen, J.; Barink, M.; Klerk, L.; Voorthuijzen, W.P.; Hovestad, A. Efficiency loss prevention in monolithically integrated thin film solar cells by improved front contact. Prog. Photovolt. Res. Appl. 2015, 23, 498–506. [Google Scholar] [CrossRef]
- Morales-Masis, M.; de Nicolas, S.M.; Holosky, J.; de Wolf, S.; Ballif, C. Low-temperature high-mobility amorphous IZO for silicon heterojunction solar cells. IEEE J. Photovolt. 2015, 5, 1340–1347. [Google Scholar] [CrossRef]
- Illiberi, A.; Kniknie, B.; van Deelen, J.; Steijvers, H.L.A.H.; Habets, D.; Simons, P.J.P.M.; Janssen, A.C.; Beckers, E.H.A. Industrial high-rate (~14 nm/s) deposition of low resistive and transparent ZnOx:Al films on glass. Sol. Energy Mater. Sol. Cells 2011, 95, 1955–1959. [Google Scholar] [CrossRef]
- Ward, J.S.; Duda, A.; Friedman, D.J.; Geisz, J.; McMahon, W.; Young, M. High aspect ratio electrodeposited Ni/Au contacts for GaAs-based III-V concentrator solar cells. Prog. Photovolt. Res. Appl. 2015, 23, 646–653. [Google Scholar] [CrossRef]
- Van Deelen, J.; Klerk, L.A.; Barink, M.; Rendering, H.; Voorthuizen, P.; Hovestad, A. Improvement strategy of transparent conductive materials using metallic grids: Modeling and experiments. Thin Solid Films 2014, 555, 159–162. [Google Scholar] [CrossRef]
- Van Deelen, J.; Frijters, C. Metallized front contact for higher efficiency CIGS cells. Sol. Energy 2017, 143, 93–99. [Google Scholar] [CrossRef]
- Hsu, P.C.; Wang, S.; Wu, H.; Narasimhan, V.K.; Kong, D.; Lee, H.R.; Cui, Y. Performance enhancement of metal nanowire transparent conducting electrodes by mesoscale metal wires. Nat. Commun. 2013, 4, 2522. [Google Scholar] [CrossRef] [PubMed]
- Kik, P.G. Catoptric electrodes: Transparent metal electrodes using shaped surfaces. Opt. Lett. 2014, 39, 5114–5117. [Google Scholar] [CrossRef] [PubMed]
- Saive, R.; Bukowsky, C.R.; Yalamanchili, S.; Boccard, M.; Saenz, T.; Borsuk, A.M.; Holman, Z.; Atwater, H.A. Effectively transparent contacts (ETCs) for solar cells. In Proceedings of the 2016 IEEE 43th Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 3612–3615. [Google Scholar]
- Van Deelen, J.; Klerk, L.; Barink, M. Optimized grid design for thin film solar panels. Sol. Energy 2014, 107, 135–144. [Google Scholar] [CrossRef]
- De, S.; Higgins, T.M.; Lyons, P.E.; Doherty, E.M.; Nirmalraj, P.N.; Blau, W.J.; Boland, J.J.; Coleman, J.N. Silver nanowire networks as flexible, transparent, conducting films: Extremely high DC to optical conductivity ratios. ACS Nano 2009, 3, 1767–1774. [Google Scholar] [CrossRef] [PubMed]
- Kwan, Y.C.G.; Le, Q.L.; Huan, C.H.A. Time to failure modeling of silver nanowire transparent conducting electrodes and effects of a reduced graphene oxide over layer. Sol. Energy Mater. Sol. Cells 2016, 144, 102–108. [Google Scholar] [CrossRef]
- Lee, J.Y.; Connor, S.T.; Cui, Y.; Peumans, P. Solution-processed metal nanowire mesh transparent electrodes. Nano Lett. 2008, 8, 689–692. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.G.; Park, H.J.; Ahn, S.H.; Guo, L.J. Transparent Cu nanowire mesh electrode on flexible substrates fabricated by transfer printing and its application in organic solar cells. Sol. Energy Mater. Sol. Cells 2010, 94, 1179–1184. [Google Scholar] [CrossRef]
- Van de Groep, J.; Gupta, D.; Verschuuren, M.A.; Wienk, M.M.; Janssen, R.A.J.; Polman, A. Large-area soft-imprinted nanowire networks as light trapping transparent conductor. Sci. Rep. 2015, 51, 11414. [Google Scholar] [CrossRef] [PubMed]
- Van de Groep, J.; Spinelli, P.; Polman, A. Transparent conducting silver nanowire networks. Nano Lett. 2012, 123, 138–144. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.G.; Guo, L.J. Nanoimprinted semitransparent metal electrodes and their application in organic light-emitting diodes. Adv. Mater. 2007, 19, 1391–1396. [Google Scholar] [CrossRef]
- Afshinmanesh, F.; Curto, A.G.; Milaninia, K.M.; van Hulst, N.F.; Brongersma, M.L. Transparent metallic fractal electrodes for semiconductor devices. Nano Lett. 2014, 14, 5068–5074. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, T.; Tsustumi, E.; Masunaga, K.; Fujimoto, A.; Asakawa, K. Transparent aluminum nanomesh electrode fabricated by nanopatterning using self-assembled nanoparticles. Appl. Phys. Express 2011, 4, 417–423. [Google Scholar] [CrossRef]
- Landy, N.; Smith, D.R. A full-parameter unidirectional metamaterial cloak for microwaves. Nat. Mater. 2013, 12, 25–28. [Google Scholar] [CrossRef] [PubMed]
- Schumann, M.F.; Wiesendanger, S.; Goldschmidt, J.C.; Bläsi, B.; Bittkau, K.; Paetzhold, U.W.; Sprafke, A.; Wehrspohn, R.B.; Rockstuhl, C.; Wegener, M. Cloaked contact grids on solar cells by coordinate transformations: Designs and prototypes. Optica 2015, 2, 850–853. [Google Scholar] [CrossRef]
- Chen, F.H.; Pathreeker, S.; Kaur, J.; Hosein, A.D. Increasing light capture in silicon solar cells with encapsulants incorporating air prisms to reduce metallic contact losses. Opt. Express 2016, 24, A1419–A1439. [Google Scholar] [CrossRef] [PubMed]
- Narasimhan, V.K.; Hymel, T.M.; Lai, R.A.; Cui, Y. Hybrid metal-semiconductor nanostructure for ultrahigh optical absorption and low electrical resistance at optoelectronic interfaces. ACS Nano 2015, 9, 1590–1597. [Google Scholar] [CrossRef] [PubMed]
- John, J.; Tang, Y.Y.; Rothstein, J.P.; Watkins, J.J.; Carter, K.R. Large-area; continuous roll-to-roll nanoimprinting with PFPE composite molds. Nanotechnology 2013, 25, 505307. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Wachters, A.J.H.; van Deelen, J.; Mourad, M.C.D.; Buskens, P.J.P. A study on the optics of copper indium gallium (di)selenide (CIGS) solar cells with ultra-thin absorber layers. Opt. Express 2014, 22, A425–A437. [Google Scholar] [CrossRef] [PubMed]
- Burghoorn, M.; Kniknie, B.; van Deelen, J.; Xu, M.; Vroon, Z.; van Ee, R.; van de Belt, R.; Buskens, P. Improving the efficiency of copper indium gallium (Di-)selenide (CIGS) solar cells through integration of a moth-eye textured resist with a refractive index similar to aluminum doped zinc oxide. AIP Adv. 2014, 4, 127154. [Google Scholar] [CrossRef]
- Buskens, P.; Burghoorn, M.; Mourad, M.C.D.; Vroon, Z. Antireflective coatings for glass and transparent polymers. Langmuir 2016, 32, 6781–6793. [Google Scholar] [CrossRef] [PubMed]
- Catrysse, P.B.; Fan, S. Nanopatterned metallic films for use as transparent conductive electrodes in optoelectronic devices. Nano Lett. 2010, 10, 2944–2949. [Google Scholar] [CrossRef] [PubMed]
- Kuang, P.; Park, J.-M.; Leung, W.; Mahadevapuram, R.C.; Nalwa, K.S.; Kim, T.-G.; Chaudhary, S.; Ho, K.-M.; Constant, K. A new architecture for transparent electrodes: Relieving the trade-off between electrical conductivity and optical transmittance. Adv. Mater. 2011, 23, 2469–2473. [Google Scholar] [CrossRef] [PubMed]
- Saive, R.; Borsuk, A.M.; Emmer, H.S.; Bukowsky, C.R.; Lloyd, J.V.; Yalamanchili, S.; Atwater, H.A. Effectively Transparent Front Contacts for Optoelectronic Devices. Adv. Opt. Mater. 2011, 23, 2469–2473. [Google Scholar] [CrossRef]
- Van Deelen, J.; Illiberi, A.; Kniknie, B.; Steijvers, H.; Lankhorst, A.; Simons, P. APCVD of ZnO:Al, insight and control by modeling. Surf. Coat. Technol. 2013, 230, 239–244. [Google Scholar] [CrossRef]
- Gao, T.; Leu, P.W. The role of propagating modes in silver nanowire arrays for transparent electrodes. Opt. Express 2013, 21, A419–A429. [Google Scholar] [CrossRef] [PubMed]
- Brongersma, M.L.; Cui, Y.; Fan, S. Light management for photovoltaics using high-index nanostructures. Nat. Mater. 2014, 13, 451–460. [Google Scholar] [CrossRef] [PubMed]
- Jarzembowski, J.; Maiberg, M.; Obereigner, F.; Kaufmann, K.; Krause, S.; Scheer, R. Optical and electrical characterization of Cu(In,Ga)Se2 thin film solar cells with varied absorber layer thickness. Thin Solid Films 2015, 576, 75–80. [Google Scholar] [CrossRef]
- Lundberg, O.; Bodegard, M.; Malmström, J.; Stolt, L. Influence of the Cu(In,Ga)Se2 Thickness and Ga Grading on Solar Cell Performance. Prog. Photovolt. Res. Appl. 2003, 11, 77–88. [Google Scholar] [CrossRef]
- Fujiwara, H.; Kondo, M. Effects of carrier concentration on the dielectric function of ZnO:Ga and In2O3:Sn studied by spectroscopic ellipsometry: Analysis of free-carrier and band-edge absorption. Phys. Rev. B 2005, 71, 075109. [Google Scholar] [CrossRef]
- Schultz, L.G.; Tangherlini, F.R. Optical Constants of Silver, Gold, Copper, and Aluminum. I. The Absorption Coefficient k. J. Opt. Soc. Am. 1954, 44, 357–362. [Google Scholar] [CrossRef]
- Schultz, L.G.; Tangherlini, F.R. Optical Constants of Silver, Gold, Copper, and Aluminum. II. The Index of Refraction n. J. Opt. Soc. Am. 1954, 44, 362–368. [Google Scholar] [CrossRef]









© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deelen, J.V.; Omar, A.; Barink, M. Optical Design of Textured Thin-Film CIGS Solar Cells with Nearly-Invisible Nanowire Assisted Front Contacts. Materials 2017, 10, 392. https://doi.org/10.3390/ma10040392
Deelen JV, Omar A, Barink M. Optical Design of Textured Thin-Film CIGS Solar Cells with Nearly-Invisible Nanowire Assisted Front Contacts. Materials. 2017; 10(4):392. https://doi.org/10.3390/ma10040392
Chicago/Turabian StyleDeelen, Joop Van, Ahmed Omar, and Marco Barink. 2017. "Optical Design of Textured Thin-Film CIGS Solar Cells with Nearly-Invisible Nanowire Assisted Front Contacts" Materials 10, no. 4: 392. https://doi.org/10.3390/ma10040392
APA StyleDeelen, J. V., Omar, A., & Barink, M. (2017). Optical Design of Textured Thin-Film CIGS Solar Cells with Nearly-Invisible Nanowire Assisted Front Contacts. Materials, 10(4), 392. https://doi.org/10.3390/ma10040392