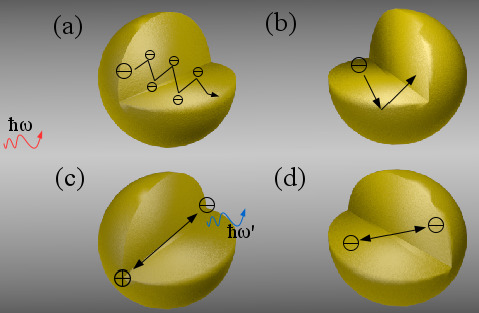
Microscopic Electron Dynamics in Metal Nanoparticles for Photovoltaic Systems
Abstract
:1. Introduction
2. Results
2.1. Classical and Phenomenological Approaches
2.2. Random Phase Approximation
2.3. Nonlocal Optical Response
2.4. Remarks on Retardation, Multipolar Response and Computational Feasibility
3. Discussion
3.1. Single Metal Nanoparticles
3.2. Dimers
3.3. Summary
4. Methods
4.1. Electron Dynamics within the RPA
4.2. Electron Dynamics with the Hydrodynamic Model
4.3. Simulations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Weidinger, I.; Ly, K.H.; Öner, H.I.; Querebillo, C.; David, C.; Gernert, U.; Walter, C.; Driess, M.; Leimkühler, S. High electromagnetic field enhancement of TiO2 nanotubes electrodes. Angew. Chem. 2018, 57, 7225–7229. [Google Scholar] [CrossRef]
- Atwater, H.A.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Zhang, G.; Li, H.M.; Yoo, W.J. Localized Surface Plasmon Resonances Caused by Ag Nanoparticles on SiN for Solar Cell Applications. J. Korean Phys. Soc. 2010, 56, 1488–1491. [Google Scholar]
- David, C.; Connolly, J.P.; Chaverri Ramos, C.; García de Abajo, F.J.; Sánchez Plaza, G. Theory of random nanoparticle layers in photovoltaic devices applied to self-aggregated metal samples. Sol. Energy Mater. Sol. Cells 2013, 109, 294–299. [Google Scholar] [CrossRef]
- Cortés-Juan, F.; Chaverri Ramos, C.; Connolly, J.P.; David, C.; García de Abajo, F.J.; Hurtado, J.; Mihailetchi, V.D.; Ponce-Alcántara, S.; Sánchez, G. Effect of Ag nanoparticles integrated within antireflection coatings for solar cells. J. Renew. Sustain. Energy 2013, 5, 033116. [Google Scholar] [CrossRef] [Green Version]
- David, C. Multi-type particle layer improved light trapping for photovoltaic applications. Appl. Opt. 2016, 55, 7980–7986. [Google Scholar] [CrossRef] [PubMed]
- Jang, Y.H.; Jang, Y.J.; Kim, S.; Quan, L.N.; Chung, K.; Kim, D.H. Plasmonic Solar Cells: From Rational Design to Mechanism Overview. Chem. Rev. 2016, 116, 14982–15034. [Google Scholar] [CrossRef] [PubMed]
- Cushing, S.K.; Li, J.; Meng, F.; Senty, T.R.; Suri, S.; Zhi, M.; Li, M.; Bristow, A.D.; Wu, N. Photocatalytic Activity Enhanced by Plasmonic Resonant Energy Transfer from Metal to Semiconductor. J. Am. Chem. Soc. 2012, 134, 15033–15041. [Google Scholar] [CrossRef] [PubMed]
- Akimov, A.V.; Neukirch, A.J.; Prezhdo, O.V. Theoretical Insights into Photoinduced Charge Transfer and Catalysis at Oxide Interfaces. Chem. Rev. 2013, 113, 4496–4565. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chen, Y.L.; Liu, R.S.; Tsai, D.P. Plasmonic photocatalysis. Rep. Prog. Phys. 2013, 76, 046401. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.C.; Dai, Y.; Yu, L.; Huang, B.B. Energy transfer in plasmonic photocatalytic composites. Light Sci. Appl. 2016, 5, e16017. [Google Scholar] [CrossRef]
- David, C. Two-fluid, hydrodynamic model for spherical electrolyte systems. Sci. Rep. 2018, 8, 7544. [Google Scholar] [CrossRef] [PubMed]
- Lakhotiya, H.; Nazir, A.; Madsen, S.P.; Christiansen, J.; Eriksen, E.; Vester-Petersen, J.; Johannsen, S.R.; Jeppesen, B.R.; Balling, P.; Larsen, A.N.; et al. Plasmonically enhanced upconversion of 1500nm light via trivalent Er in a TiO2 matrix. Appl. Phys. Lett. 2016, 109, 263102. [Google Scholar] [CrossRef]
- Yuan, Z.; Pucker, G.; Marconi, A.; Sgrignuoli, F.; Anopchenko, A.; Jestin, Y.; Ferrario, L.; Bellutti, P.; Pavesi, L. Silicon nanocrystals as a photoluminescence down shifter for solar cells. Sol. Energy Mater. Sol. Cells 2011, 95, 1224–1227. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef] [Green Version]
- Liebsch, A. Surface-plasmon dispersion and size dependence of Mie resonance: Silver versus simple metals. Phys. Rev. B 1993, 48, 11317–11328. [Google Scholar] [CrossRef]
- Larkin, I.A.; Stockman, M.I. Imperfect Perfect Lens. Nano Lett. 2005, 5, 339–343. [Google Scholar] [CrossRef] [PubMed]
- Zuloaga, J.; Prodan, E.; Nordlander, P. Quantum Description of the Plasmon Resonances of a Nanoparticle Dimer. Nano Lett. 2009, 9, 887–891. [Google Scholar] [CrossRef] [PubMed]
- Lermé, J.; Palpant, B.; Prével, B.; Cottancin, E.; Pellarin, M.; Treilleux, M.; Vialle, J.L.; Perez, A.; Broyer, M. Optical Properties of gold metal clusters: A time-dependent local-density-approximation investigation. Eur. Phys. J. D 1998, 4, 95–108. [Google Scholar] [CrossRef]
- Savage, K.J.; Hawkeye, M.M.; Esteban, R.; Borisov, A.G.; Aizpurua, J.; Baumberg, J.J. Revealing the quantum regime in tunnelling plasmonics. Nature 2012, 491, 574–577. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Esteban, R.; Borisov, A.G.; Nordlander, P.; Aizpurua, J. Bridging quantum and classical plasmonics with a quantum-corrected model. Nat. Commun. 2012, 3, 825. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prodan, E.; Nordlander, P.; Halas, N.J. Electronic Structure and Optical Properties of Gold Nanoshells. Nano Lett. 2003, 3, 1411–1415. [Google Scholar] [CrossRef]
- Danckwerts, M.; Novotny, L. Optical Frequency Mixing at Coupled Gold Nanoparticles. Phys. Rev. Lett. 2007, 98, 026104. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.S.; Pastoriza-Santos, I.; Rodríguez-González, B.; de Abajo, F.J.G.; Liz-Marzán, L.M. High-yield synthesis and optical response of gold nanostars. Nanotechnology 2008, 19, 015606. [Google Scholar] [CrossRef] [PubMed]
- Scholl, J.A.; Koh, A.L.; Dionne, J.A. Quantum plasmon resonances of individual metallic nanoparticles. Nature 2012, 483, 421–427. [Google Scholar] [CrossRef] [PubMed]
- Ciracì, C.; Hill, R.T.; Mock, J.J.; Urzhumov, Y.; Fernández-Domínguez, A.I.; Maier, S.A.; Pendry, J.B.; Chilkoti, A.; Smith, D.R. Probing the Ultimate Limits of Plasmonic Enhancement. Science 2012, 337, 1072–1074. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raza, S.; Stenger, N.; Kadkhodazadeh, S.; Fischer, S.V.; Kostesha, N.; Jauho, A.P.; Burrows, A.; Wubs, M.; Mortensen, N.A. Blueshift of the surface plasmon resonance in silver nanoparticles studied with EELS. Nanophotonics 2013, 2, 131–138. [Google Scholar] [CrossRef]
- Haberland, H. Looking from both sides. Nature 2013, 494, E1–E2. [Google Scholar] [CrossRef] [PubMed]
- Raza, S.; Kadkhodazadeh, S.; Christensen, T.; Di Vece, M.; Wubs, M.; Mortensen, N.A.; Stenger, N. Multipole plasmons and their disappearance in few-nanometer silver nanoparticles. Nat. Commun. 2015, 6, 8788. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuchs, R.; Kliewer, K.L. Surface Plasmon in a Semi-Infinite Free-Electron Gas. Phys. Rev. B 1971, 3, 2270–2278. [Google Scholar] [CrossRef]
- Ruppin, R. Optical Properties of a Plasma Sphere. Phys. Rev. Lett. 1973, 31, 1434–1437. [Google Scholar] [CrossRef]
- Ruppin, R. Optical properties of spatially dispersive dielectric spheres. J. Opt. Soc. Am. 1981, 71, 755–758. [Google Scholar] [CrossRef]
- Dasgupta, B.B.; Fuchs, R. Polarizability of a small sphere including nonlocal effects. Phys. Rev. B 1981, 24, 554–561. [Google Scholar] [CrossRef]
- Fuchs, R.; Claro, F. Multipolar response of small metallic spheres: Nonlocal theory. Phys. Rev. B 1987, 35, 3722–3727. [Google Scholar] [CrossRef]
- Rojas, R.; Claro, F.; Fuchs, R. Nonlocal Response of a small coated sphere. Phys. Rev. B 1988, 37, 6799–6808. [Google Scholar] [CrossRef]
- Ruppin, R. Optical absorption by excitons in microcrystals. J. Phys. Chem. Solids 1989, 50, 877–882. [Google Scholar] [CrossRef]
- Ruppin, R. Optical absorption by a small sphere above a substrate with inclusion of nonlocal effects. Phys. Rev. B 1992, 45, 11209–11215. [Google Scholar] [CrossRef]
- Kreibig, U.; Vollmer, M. Optical Properties of Metal Clusters; Springer: Berlin, Germany, 1995. [Google Scholar]
- Ruppin, R. Extinction properties of thin metallic nanowires. Opt. Commun. 2001, 190, 205–209. [Google Scholar] [CrossRef]
- García de Abajo, F.J. Nonlocal Effects in the Plasmons of Strongly Interacting Nanoparticles, Dimers, and Waveguides. J. Phys. Chem. C 2008, 112, 17983–17987. [Google Scholar] [CrossRef] [Green Version]
- David, C.; García de Abajo, F.J. Spatial Nonlocality in the Optical Response of Metal Nanoparticles. J. Phys. Chem. C 2011, 115, 19470–19475. [Google Scholar] [CrossRef] [Green Version]
- Bloch, F. Zur Bremsung rasch bewegter Teilchen beim Durchgang durch Materie. Z. Phys. 1933, 81, 363–376. [Google Scholar] [CrossRef]
- Eguiluz, A.; Ying, S.C.; Quinn, J.J. Influence of the electron density profile on surface plasmons in a hydrodynamic model. Phys. Rev. B 1975, 11, 2118–2121. [Google Scholar] [CrossRef]
- Sipe, J.E.; So, V.C.Y.; Fukui, M.; Stegeman, G.I. Analysis of second-harmonic generation at metal surfaces. Phys. Rev. B 1980, 21, 4389–4402. [Google Scholar] [CrossRef]
- Leung, P.T. Decay of molecules at spherical surfaces: Nonlocal effects. Phys. Rev. B 1990, 42, 7622–7625. [Google Scholar] [CrossRef]
- Aizpurua, J.; Rivacoba, A. Nonlocal effects in the plasmons of nanowires and nanocavities excited by fast electron beams. Phys. Rev. B 2008, 78, 035404. [Google Scholar] [CrossRef]
- McMahon, J.M.; Gray, S.K.; Schatz, G.C. Optical Properties of Nanowire Dimers with a Spatially Nonlocal Dielectric Function. Nano Lett. 2010, 10, 3473–3481. [Google Scholar] [CrossRef] [PubMed]
- Raza, S.; Toscano, G.; Jauho, A.P.; Wubs, M.; Mortensen, N.A. Unusual resonances in nanoplasmonic structures due to nonlocal response. Phys. Rev. B 2011, 84, 121412. [Google Scholar] [CrossRef]
- Wiener, A.; Fernández-Domínguez, A.I.; Horsfield, A.P.; Pendry, J.B.; Maier, S.A. Nonlocal Effects in the Nanofocusing Performance of Plasmonic Tips. Nano Lett. 2012, 12, 3308–3314. [Google Scholar] [CrossRef] [PubMed]
- De Ceglia, D.; Campione, S.; Vincenti, M.A.; Capolino, F.; Scalora, M. Low-damping epsilon-near-zero slabs: Nonlinear and nonlocal optical properties. Phys. Rev. B 2013, 87, 155140. [Google Scholar] [CrossRef]
- David, C.; Mortensen, N.A.; Christensen, J. Perfect imaging, epsilon-near zero phenomena and waveguiding in the scope of nonlocal effects. Sci. Rep. 2013, 3, 2526. [Google Scholar] [CrossRef] [PubMed]
- Teperik, T.V.; Nordlander, P.; Aizpurua, J.; Borisov, A.G. Robust subnanometric plasmon ruler by rescaling of the nonlocal optical response. Phys. Rev. Lett. 2013, 110, 263901. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Fernandez-Dominguez, A.I.; Wiener, A.; Maier, S.A.; Pendry, J.B. Surface Plasmons and Nonlocality: A Simple Model. Phys. Rev. Lett. 2013, 111, 093901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Christensen, T.; Yan, W.; Raza, S.; Jauho, A.P.; Mortensen, N.A.; Wubs, M. Nonlocal Response of Metallic Nanospheres Probed by Light, Electrons, and Atoms. ACS Nano 2014, 8, 1745–1758. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mortensen, N.A.; Raza, S.; Wubs, M.; Søndergaard, T.; Bozhevolnyi, S.I. A generalized non-local optical response theory for plasmonic nanostructures. Nat. Commun. 2014, 5, 3809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raza, S.; Bozhevolnyi, S.I.; Wubs, M.; Mortensen, N.A. Nonlocal optical response in metallic nanostructures. J. Phys. Condens. Matter 2015, 27, 183204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toscano, G.; Straubel, J.; Kwiatkowski, A.; Rockstuhl, C.; Evers, F.; Xu, H.; Mortensen, N.A.; Wubs, M. Resonance shifts and spill-out effects in self-consistent hydrodynamic nanoplasmonics. Nat. Commun. 2015, 6, 7132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, W.; Wubs, M.; Mortensen, N.A. Projected Dipole Model for Quantum Plasmonics. Phys. Rev. Lett. 2015, 115, 137403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- David, C.; Christensen, J.; Mortensen, N.A. Spatial dispersion in two-dimensional plasmonic crystals: Large blueshifts promoted by diffraction anomalies. Phys. Rev. B 2016, 94, 165410. [Google Scholar] [CrossRef]
- Jacak, J.; Krasnyj, J.; Jacak, W.; Gonczarek, R.; Chepok, A.; Jacak, L. Surface and volume plasmons in metallic nanospheres in semiclassical RPA-type approach; Near-field coupling of surface plasmons with semiconductor substrate. Phys. Rev. B 2010, 82, 035418. [Google Scholar] [CrossRef]
- Jacak, W.A. Lorentz Friction for Surface Plasmons in Metallic Nanospheres. J. Phys. Chem. C 2015, 119, 6749–6759. [Google Scholar] [CrossRef]
- Kluczyk, K.; Jacak, W. Damping-induced size effect in surface plasmon resonance in metallic nano-particles: Comparison of RPA microscopic model with numerical finite element simulation (COMSOL) and Mie approach. J. Quant. Spectr. Radiat. Transf. 2016, 168, 78–88. [Google Scholar] [CrossRef]
- Jacak, W.; Popko, E.; Henrykowski, A.; Zielony, E.; Gwozdz, K.; Luka, G.; Pietruszka, R.; Witkowski, B.; Wachnicki, L.; Godlewski, M.; et al. On the size dependence and spatial range for the plasmon effect in photovoltaic efficiency enhancement. Sol. Energy Mater. Sol. Cells 2016, 147, 1–16. [Google Scholar] [CrossRef]
- Kluczyk, K.; David, C.; Jacak, W.A. On quantum approach to modeling of plasmon photovoltaic effect. JOSA B 2017, 34, 2115–2127. [Google Scholar] [CrossRef]
- David, C.; García de Abajo, F.J. Surface Plasmon Dependence on the Electron Density Profile at Metal Surfaces. ACS Nano 2014, 8, 9558–9566. [Google Scholar] [CrossRef] [PubMed]
- Ciracì, C. Current-dependent potential for nonlocal absorption in quantum hydrodynamic theory. Phys. Rev. B 2017, 95. [Google Scholar] [CrossRef]
- De Abajo, F.J.G. Multiple scattering of radiation in clusters of dielectrics. Phys. Rev. B 1999, 60, 6086–6102. [Google Scholar] [CrossRef]
- Kreibig, U.; Fragstein, C.V. The Limitation of Electron Mean Free Path in Small Silver Particles. Z. Phys. 1969, 224, 307–323. [Google Scholar] [CrossRef]
- Coronado, E.A.; Schatz, G.C. Surface plasmon broadening for arbitrary shape nanoparticles: A geometrical probability approach. J. Chem. Phys. 2003, 119, 3926–3934. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshits, E.M. Field Theory; Nauka: Moscow, Russia, 1973. [Google Scholar]
- David, C.; Christensen, J. Extraordinary optical transmission through nonlocal holey metal films. Appl. Phys. Lett. 2017, 110, 261110. [Google Scholar] [CrossRef]
- Abrikosov, A.A. Fundamentals of the Theory of Metals; North-Holland: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Maack, J.R.; Mortensen, N.A.; Wubs, M. Size-dependent nonlocal effects in plasmonic semiconductor particles. EPL (Europhys. Lett.) 2017, 119, 17003. [Google Scholar] [CrossRef] [Green Version]
- Maack, J.R.; Mortensen, N.A.; Wubs, M. Two-fluid hydrodynamic model for semiconductors. Phys. Rev. B 2018, 97, 115415. [Google Scholar] [CrossRef] [Green Version]
- Pines, D. Elementary Excitations in Solids; Advanced Book Program; Perseus Books: Reading, MA, USA, 1999. [Google Scholar]
- Lang, N.D.; Kohn, W. Theory of metal Surfaces: Charge Density and Surface Energy. Phys. Rev. B 1970, 1, 4555–4568. [Google Scholar] [CrossRef]
- Low, F.E. Classical Field Theory: Electromagnetism and Gravitation; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1975. [Google Scholar]
- Tserkezis, C.; Stefanou, N.; Wubs, M.; Mortensen, N.A. Molecular fluorescence enhancement in plasmonic environments: Exploring the role of nonlocal effects. Nanoscale 2016, 8, 17532–17541. [Google Scholar] [CrossRef] [PubMed]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kluczyk, K.; Jacak, L.; Jacak, W.; David, C. Microscopic Electron Dynamics in Metal Nanoparticles for Photovoltaic Systems. Materials 2018, 11, 1077. https://doi.org/10.3390/ma11071077
Kluczyk K, Jacak L, Jacak W, David C. Microscopic Electron Dynamics in Metal Nanoparticles for Photovoltaic Systems. Materials. 2018; 11(7):1077. https://doi.org/10.3390/ma11071077
Chicago/Turabian StyleKluczyk, Katarzyna, Lucjan Jacak, Witold Jacak, and Christin David. 2018. "Microscopic Electron Dynamics in Metal Nanoparticles for Photovoltaic Systems" Materials 11, no. 7: 1077. https://doi.org/10.3390/ma11071077
APA StyleKluczyk, K., Jacak, L., Jacak, W., & David, C. (2018). Microscopic Electron Dynamics in Metal Nanoparticles for Photovoltaic Systems. Materials, 11(7), 1077. https://doi.org/10.3390/ma11071077