A Three-Phase Model Characterizing the Low-Velocity Impact Response of SMA-Reinforced Composites under a Vibrating Boundary Condition
Abstract
:1. Introduction
2. The Three-Phase Model
2.1. Material Property of the Glass Fiber/Epoxy Composite Laminate
2.2. Material Property of the SMA
2.3. Material Property of the Interphase
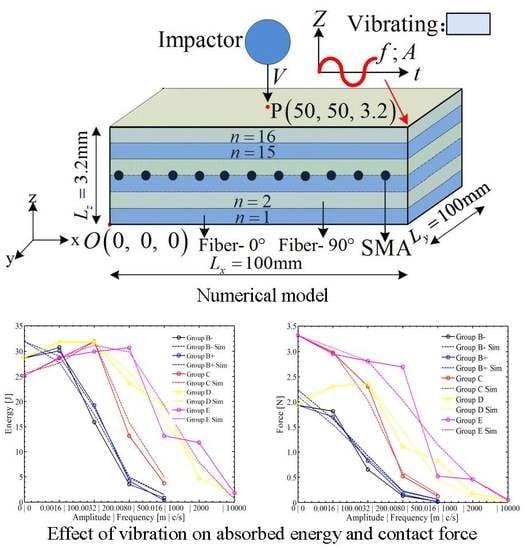
2.4. Boundary Condition
3. The Effect of the Fixed Boundary Condition on Impact Resistance
3.1. Composite Laminates
3.2. Simulation Result: Damage State During the Impact Process
3.3. Simulation Result: Absorbed Energy and Contact Force
4. The Effect of the Vibrating Boundary Condition on Impact Resistance
4.1. The Effect of Amplitude
4.2. The Effect of Frequency
4.3. Statistical Analysis of the Damage State
4.4. Mathematical Expression: Effect of Amplitude and Frequency
5. Conclusions
- (1)
- Under a smaller amplitude (A < 0.0032 m) and a lower frequency (f < 500 cycles/s), the absorbed energy and contact force of composite laminates are similar to that under a fixed boundary condition. In contrast, both a high frequency and a high amplitude can weaken the impact resistance of composite laminates, where extensive damage can be observed rather than a hole-shaped damage region.
- (2)
- The absolute value of amplitude has a greater influence on the impact resistance than the movement direction of the laminates at the initial time. The absorbed energy and contact force in the positive direction are about 20% larger than that in the negative direction.
- (3)
- Embedding an SMA can improve the impact resistance of composite laminates due to the superelasticity. In this study, embedding an SMA was found to increase the absorbed energy and contact force by about 15–30%. Also, embedding an SMA can change the damage morphology with respect to shape and proportion.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| amplitude | |
| , | start and finish temperature of austenite phase |
| , | material parameters of SMA |
| , | thermal coefficient of martensite phase and austenite phase |
| stiffness matrix | |
| , , , | damage variables |
| , , | absorbed energy, maximum value of energy, and absorbed energy at 0.01 s |
| , | elastic modulus of laminate in the i-direction, shear modulus in the ij-direction |
| , , | elastic modulus of SMA, elastic modulus for martensite phase and austenite phase |
| , , | contact force, maximum value of force, average value of force |
| frequency | |
| , | parameters of the relaxation modulus |
| , | parameter related to amplitude, parameter related to frequency |
| , , | sample dimension in the x, y, and z direction |
| , | start and finish temperature of martensite phase |
| , | mass, parameters related to amplitude |
| parameters related to frequency | |
| , , | ultimate shear strength in the 23, 13, and 12 direction |
| , | reduction factors |
| temperature | |
| , , , | time, new time variable, time parameters of the relaxation modulus, total time |
| , | initial velocity, velocity increment |
| , | tensile strength and compressive strength in the longitudinal direction |
| , | tensile strength and compressive strength in the transverse direction |
| strain of laminate in the ij-direction | |
| , | strain of SMA, maximum residual strain of SMA |
| , | strain of interphase, strain rate of interphase |
| thermal coefficient | |
| stress in the ij-direction | |
| , | stress of SMA, stress of interphase |
| Poisson’s ratio of laminate in the ij-direction | |
| transformation coefficient | |
| , , | martensite fraction, martensite fraction of stress, and temperature effect |
| , , | martensite fraction at the initial state, initial stress, and initial temperature |
References
- Biron, M. Thermoplastics and Thermoplastic Composites, 2nd ed.; William Andrew: Waltham, MA, USA, 2013. [Google Scholar]
- Li, M.; Gu, Y.; Liu, Y. Interfacial improvement of carbon fiber/epoxy composites using a simple process for depositing commercially functionalized carbon nanotubes on the fibers. Carbon 2013, 52, 109–121. [Google Scholar] [CrossRef]
- Mortazavian, S.; Fatemi, A. Effects of fiber orientation and anisotropy on tensile strength and elastic modulus of short fiber reinforced polymer composites. Compos. Part. B Eng. 2015, 72, 116–129. [Google Scholar] [CrossRef]
- Mortazavian, S.; Fatemi, A. Fatigue behavior and modeling of short fiber reinforced polymer composites: A literature review. Int. J. Fatigue 2015, 70, 297–321. [Google Scholar] [CrossRef]
- Thomason, J.L. The influence of fibre length, diameter and concentration on the strength and strain to failure of glass fibre-reinforced polyamide 6,6. Compos. Part. A 2008, 39, 1618–1624. [Google Scholar] [CrossRef] [Green Version]
- Thomason, J.L. The influence of fibre length, diameter and concentration on the modulus of glass fibre reinforced polyamide 6,6. Compos. Part. A 2008, 39, 1732–1738. [Google Scholar] [CrossRef] [Green Version]
- Thomason, J.L. The influence of fibre length, diameter and concentration on the impact performance of long glass-fibre reinforced polyamide 6,6. Compos. Part. A 2009, 40, 114–124. [Google Scholar] [CrossRef] [Green Version]
- Uematsu, H.; Suzuki, Y.; Iemoto, Y. Effect of maleic anhydride-grafted polypropylene on the flow orientation of short glass fiber in molten polypropylene and on tensile properties of composites. Adv. Polym. Tech. 2017, 37, 1755–1763. [Google Scholar] [CrossRef]
- Zhou, Y.; Mallick, P.K. Fatigue performance of injection-molded short e-glass fiber reinforced polyamide- 6,6. II. Effects of melt temperature and hold pressure. Polym. Composite. 2011, 32, 268–276. [Google Scholar] [CrossRef]
- Cui, B.; Yao, J.; Wu, Y. Effect of cold rolling ratio on the microstructure and recovery properties of Ti-Ni-Nb-Co shape memory alloys. J. Alloy. Compd. 2019, 772, 728–734. [Google Scholar] [CrossRef]
- Jani, J.M.; Leary, M.; Subic, A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Sun, M.; Wang, Z.; Yang, B. Experimental investigation of GF/epoxy laminates with different SMAs positions subjected to low-velocity impact. Compos. Struct. 2017, 171, 170–184. [Google Scholar] [CrossRef]
- Khalili, S.M.R.; Botshekanan Dehkordi, M.; Carrera, E.; Shariyat, M. Non-linear dynamic analysis of a sandwich beam with pseudoelastic SMA hybrid composite faces based on higher order finite element theory. Compos. Struct. 2013, 96, 243–255. [Google Scholar] [CrossRef]
- Khalili, S.M.R.; Botshekanan Dehkordi, M.; Shariyat, M. Modeling and transient dynamic analysis of pseudoelastic SMA hybrid composite beam. Appl. Math. Comput. 2013, 219, 9762–9782. [Google Scholar] [CrossRef]
- Shariyat, M.; Hosseini, S.H. Accurate eccentric impact analysis of the preloaded SMA composite plates, based on a novel mixed-order hyperbolic global-local theory. Compos. Struct. 2015, 124, 140–151. [Google Scholar] [CrossRef]
- Shariyat, M.; Moradi, M.; Samaee, S. Enhanced model for nonlinear dynamic analysis of rectangular composite plates with embedded SMA wires, considering the instantaneous local phase changes. Compos. Struct. 2014, 109, 106–118. [Google Scholar] [CrossRef]
- Bienias, J.; Jakubczak, P.; Dadej, K. Low-velocity impact resistance of aluminium glass laminates—Experimental and numerical investigation. Compos. Struct. 2016, 152, 339–348. [Google Scholar] [CrossRef]
- Zhang, R.; Ni, Q.Q.; Natsuki, T. Mechanical properties of composites filled with SMA particles and short fibers. Compos. Struct. 2007, 79, 90–96. [Google Scholar] [CrossRef] [Green Version]
- Chawla, N.; Sidhu, R.S.; Ganesh, V.V. Three-dimensional visualization and microstructure-based modeling of deformation in particle-reinforced composites. Acta. Mater. 2006, 54, 1541–1548. [Google Scholar] [CrossRef]
- Susainathan, J.; Eyma, F.; De Luycker, E. Experimental investigation of impact behavior of wood-based sandwich structure. Compos. Part. A 2018, 109, 10–19. [Google Scholar] [CrossRef]
- Shariyat, M. A double-superposition global-local theory for vibration and dynamic buckling analyses of viscoelastic composite/sandwich plates: A complex modulus approach. Arch. Appl. Mech. 2011, 81, 1253–1268. [Google Scholar] [CrossRef]
- Hart, K.R.; Chia, P.X.L.; Sheridan, L.E. Mechanisms and characterization of impact damage in 2D and 3D woven fiber-reinforced composites. Compos. Part. A 2017, 101, 432–443. [Google Scholar] [CrossRef]
- Asaee, Z.; Taheri, F. Experimental and numerical investigation into the influence of stacking sequence on the low-velocity impact response of new 3D FMLs. Compos. Struct. 2016, 140, 136–146. [Google Scholar] [CrossRef]
- Shariyat, M.; Hosseini, S.H. Eccentric impact analysis of pre-stressed composite sandwich plates with viscoelastic cores: A novel global-local theory and a refined contact law. Compos. Struct. 2014, 117, 333–345. [Google Scholar] [CrossRef]
- Suzuki, Y.; Suzuki, T.; Todoroki, A. Smart lightning protection skin for real-time load monitoring of composite aircraft structures under multiple impacts. Compos. Part. A 2014, 67, 44–54. [Google Scholar] [CrossRef]
- Liu, H.; Falzon, B.G.; Tan, W. Predicting the Compression-After-Impact (CAI) strength of damage-tolerant hybrid unidirectional/woven carbon-fibre reinforced composite laminates. Compos. Part A 2018, 105, 189–202. [Google Scholar] [CrossRef]
- Liu, C.J.; Todd, M.D.; Zheng, Z.L. A nondestructive method for the pretension detection in membrane structures based on nonlinear vibration response to impact. Struct. Health. Monit. 2018, 17, 67–79. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, Y. An impact-based broadband aeroelastic energy harvester for concurrent wind and base vibration energy harvesting. Appl. Energ. 2018, 212, 233–243. [Google Scholar] [CrossRef]
- Shahdin, A.; Morlier, J.; Mezeix, L. Evaluation of the impact resistance of various composite sandwich beams by vibration tests. Shock. Vib. 2013, 18, 789–805. [Google Scholar] [CrossRef]
- Li, W.; Zheng, H.; Sun, G. The moving least squares based numerical manifold method for vibration and impact analysis of cracked bodies. Eng. Fract. Mech. 2017, 190, 410–434. [Google Scholar] [CrossRef]
- Pérez, M.A.; Oller, S.; Felippa, C.A. Micro-mechanical approach for the vibration analysis of CFRP laminates under impact-induced damage. Compos. Part B. Eng. 2015, 83, 306–316. [Google Scholar] [CrossRef] [Green Version]
- Miramini, A.; Kadkhodaei, M.; Alipour, A. Analysis of interfacial debonding in shape memory alloy wire-reinforced composites. Smart. Mater. Struct. 2015, 25, 015032. [Google Scholar] [CrossRef]
- Chang, M.; Wang, Z.; Liang, W. A visco-hyperelastic model for short fiber reinforced polymer composites: Reinforcement and fracture mechanisms. Text. Res. J. 2017, 88, 2727–2740. [Google Scholar] [CrossRef]
- Chang, M.; Wang, Z.; Liang, W. A novel failure analysis of SMA reinforced composite plate based on a strain-rate-dependent model: Low-high velocity impact. J. Mater. Res. Technol. 2018. [Google Scholar] [CrossRef]
- Hashin, Z. Failure criteria for unidirectional composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Puck, A.; Schürmann, H. Failure analysis of FRP laminates by means of physically based phenomenological models. Compos. Sci. Technol. 1998, 58, 1045–1067. [Google Scholar] [CrossRef]
- Brinson, L.C.; Lammering, R. Finite element analysis of the behavior of shape memory alloys and their applications. Int. J. Solids. Struct. 1993, 30, 3261–3280. [Google Scholar] [CrossRef]
- Brinson, L.C. One-dimensional constitutive behavior of shape memory alloys: Thermomechanical derivation with non-constant material functions and redefined martensite internal variable. J. Intell. Mat. Syst. Struct. 1993, 4, 229–242. [Google Scholar] [CrossRef]























| Mechanical Constants | Values |
|---|---|
| Young’s modulus/GPa (E1, E2, E3) | 55.2, 18.4, 18.4 |
| Poisson’s ratio (, , ) | 0.27, 0.27, 0.43 |
| Shear modulus/GPa (E12, E13, E23) | 13.8, 13.8, 13.8 |
| Ultimate tensile stress/MPa (XT, YT, ZT) | 1656, 73.8, 73.8 |
| Ultimate compressive stress/MPa (XC, YC, ZC) | 1656, 91.8, 91.8 |
| Ultimate shear stress/MPa (S12, S13, S23) | 117.6, 117.6, 117.6 |
| Stacking Sequence | Impact Energy/J | |
|---|---|---|
| Group A1 | [0°,90°]8 | 32 |
| Group A2 | [0°,90°]8 | 64 |
| Group A3 | [(0°,90°)4,SMA, (0°,90°)4] | 32 |
| Group A4 | [(0°,90°)4,SMA, (0°,90°)4] | 64 |
| Group B1 | Group B2 | Group B3 | Group B4 | Group B5 | Group B6 | Group B7 | Group B8 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A (m) | 0.0016 | −0.0016 | 0.0032 | −0.0032 | 0.008 | −0.008 | 0.016 | −0.016 | ||||||||
| f (c/s) | 1000 | |||||||||||||||
| SMA Stacking | NO [0°,90°]8 | |||||||||||||||
| Group C1 | Group C2 | Group C3 | Group C4 | |||||||||||||
| A (m) | 0.0016 | 0.0032 | 0.008 | 0.016 | ||||||||||||
| f (c/s) | 1000 | |||||||||||||||
| SMA Stacking | YES [(0°,90°)4, SMA, (0°,90°)4] | |||||||||||||||
| Group D1 | Group D2 | Group D3 | Group D4 | Group D5 | ||||||||||||
| A (m) | 0.0032 | |||||||||||||||
| f (c/s) | 100 | 200 | 500 | 2000 | 10,000 | |||||||||||
| SMA Stacking | NO [0°,90°]8 | |||||||||||||||
| Group E1 | Group E2 | Group E3 | Group E4 | Group E5 | ||||||||||||
| A (m) | 0.0032 | |||||||||||||||
| f (c/s) | 100 | 200 | 500 | 2000 | 10,000 | |||||||||||
| SMA Stacking | YES [(0°,90°)4, SMA, (0°,90°)4] | |||||||||||||||
| A1 | B1 | B2 | B3 | B4 | B5 | B6 | A7 | B8 | |
|---|---|---|---|---|---|---|---|---|---|
| Emax (J) | 32 | 32 | 32 | 21.67 | 18.27 | 4.30 | 3.72 | 0.30 | 0.80 |
| Et= 0.01s (J) | 28.70 | 30.04 | 30.79 | 9.24 | 5.90 | 4.24 | 3.56 | 0.30 | 0.80 |
| Fmax (N) | 7.04 | 7.74 | 7.69 | 7.92 | 7.35 | 8.39 | 6.86 | 0.86 | 1.13 |
| Favg (N) | 1.93 | 1.70 | 1.81 | 0.83 | 0.65 | 0.16 | 0.13 | 0.01 | 0.02 |
| A3 | C1 | C2 | C3 | C4 | |||||
| Emax (J) | 32 | 32 | 32 | 13.20 | 3.74 | ||||
| Et= 0.01s (J) | 25.14 | 28.60 | 31.97 | 13.17 | 3.74 | ||||
| Fmax (N) | 6.89 | 10.77 | 10.56 | 10.52 | 8.71 | ||||
| Favg (N) | 3.32 | 2.98 | 2.31 | 0.52 | 0.12 | ||||
| D1 | D2 | D3 | D4 | D5 | |||||
| Emax (J) | 32 | 32 | 25.38 | 6.21 | 1.75 | ||||
| Et= 0.01s (J) | 31.98 | 31.92 | 23.68 | 4.69 | 1.74 | ||||
| Fmax (N) | 7.40 | 7.23 | 7.45 | 7.29 | 1.44 | ||||
| Favg (N) | 2.31 | 2.36 | 1.11 | 0.17 | 0.06 | ||||
| E1 | E2 | E3 | E4 | E5 | |||||
| Emax (J) | 32 | 32 | 32 | 11.86 | 1.79 | ||||
| Et= 0.01s (J) | 28.77 | 29.94 | 30.70 | 11.86 | 1.79 | ||||
| Fmax (N) | 10.15 | 9.79 | 11.92 | 9.02 | 2.36 | ||||
| Favg (N) | 2.95 | 2.81 | 2.69 | 0.46 | 0.05 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, M.; Kong, F.; Sun, M.; He, J. A Three-Phase Model Characterizing the Low-Velocity Impact Response of SMA-Reinforced Composites under a Vibrating Boundary Condition. Materials 2019, 12, 7. https://doi.org/10.3390/ma12010007
Chang M, Kong F, Sun M, He J. A Three-Phase Model Characterizing the Low-Velocity Impact Response of SMA-Reinforced Composites under a Vibrating Boundary Condition. Materials. 2019; 12(1):7. https://doi.org/10.3390/ma12010007
Chicago/Turabian StyleChang, Mengzhou, Fangyun Kong, Min Sun, and Jian He. 2019. "A Three-Phase Model Characterizing the Low-Velocity Impact Response of SMA-Reinforced Composites under a Vibrating Boundary Condition" Materials 12, no. 1: 7. https://doi.org/10.3390/ma12010007
APA StyleChang, M., Kong, F., Sun, M., & He, J. (2019). A Three-Phase Model Characterizing the Low-Velocity Impact Response of SMA-Reinforced Composites under a Vibrating Boundary Condition. Materials, 12(1), 7. https://doi.org/10.3390/ma12010007