A Numerical Study of Slip System Evolution in Ultra-Thin Stainless Steel Foil
Abstract
:1. Introduction
2. Crystal Plasticity Model
3. Finite Element Model for Stainless Steel Foil
- (1)
- The back surface center node was set at X = 0, Y = 0, Z = 0 to avoid the rigid motion of the RVE model as a whole.
- (2)
- The back surface was set at X = 0. There was no constraint in the Y and Z directions, so that plastic deformation could occur in the Y and Z directions.
- (3)
- The front surface was set in a uniform tensile displacement along in the X-direction.
4. Results and Discussion
4.1. Microscopic Stress and Strain Distribution of G411
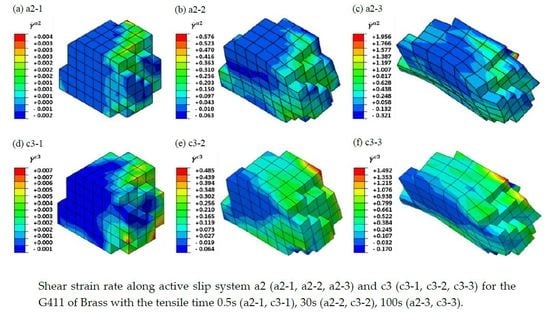
4.2. Slip System Evolution of G411 with the Typical Grain Orientations
4.3. Stress and Strain Curves of Typical Texture Orientation Dominant Polycrystalline
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiao, H.; Ren, Z.; Liu, X. New mechanism describing the limiting producible thickness in ultra-thin strip rolling. Int. J. Mech. Sci. 2017, 133, 788–793. [Google Scholar] [CrossRef]
- Chen, Z.J.; Chen, X.; Zhou, T.P. Microstructure and mechanical properties of J55ERW steel pipe processed by on-line spray water cooling. Metals 2017, 7, 150. [Google Scholar] [CrossRef]
- Daming, N.; Zhen, L.; Kaifeng, Z. Grain size effect of commercial pure titanium foils on mechanical properties, fracture behaviors and constitutive models. J. Mater. Eng. Perform. 2017, 26, 1283–1292. [Google Scholar] [CrossRef]
- Fu, M.W.; Chan, W.L. Geometry and grain size effects on the fracture behavior of sheet metal in microscale plastic deformation. Mater. Des. 2011, 32, 4738–4746. [Google Scholar] [CrossRef]
- Grogan, J.A.; Leen, S.B.; McHugh, P.E. Influence of statistical size effects on the plastic deformation of coronary stents. J. Mech. Behav. Biomed. Mater. 2013, 20, 61–76. [Google Scholar] [CrossRef] [PubMed]
- Furushima, T.; Tsunezaki, H.; Manabe, K.I.; Alexsandrov, S. Ductile fracture and free surface roughening behaviors of pure copper foils for micro/meso-scale forming. Int. J. Mach. Tools Manuf. 2014, 76, 34–48. [Google Scholar] [CrossRef]
- Chen, S.D.; Liu, X.H.; Liu, L.Z. Symmetric and asymmetric rolling pure copper foil: crystal plasticity finite element simulation and experiments. Acta Metall. Sin. (Engl. Lett.) 2015, 25, 1024–1033. [Google Scholar] [CrossRef]
- Ye, W.; Efthymiadis, P.; Pinna, C.; Ma, A.; Shollock, B.; Dashwood, R. Experimental and modelling study of fatigue crack initiation in an Aluminium beam with a hole under 4-point bending. Int. J. Solids Struct. 2018, 138, 87–96. [Google Scholar] [CrossRef]
- Ma, X.; Zhao, J.; Du, W.; Zhang, X.; Jiang, L.; Jiang, Z. An analysis of ridging of ferritic stainless steel 430. Mater. Sci. Eng. A 2017, 685, 358–366. [Google Scholar] [CrossRef]
- Bishoyi, B.; Debta, M.K.; Yadav, S.K.; Sabat, R.K.; Sahoo, S.K. Simulation of texture evolution during uniaxial deformation of commercially pure Titanium. IOP Conf. Ser. Mater. Sci. Eng. 2018, 338, 012038. [Google Scholar] [CrossRef]
- Singh, J.; Kim, M.S.; Choi, S.H. The effect of initial texture on micromechanical deformation behaviors in Mg alloys under a mini-V-bending test. Int. J. Plast. 2019, 117, 33–57. [Google Scholar] [CrossRef]
- Si, L.Y.; Lü, C.; Tieu, A.K.; Liu, X.H. Simulation of polycrystalline aluminum tensile test with crystal plasticity finite element method. Trans. Nonferrous Metals Soc. China 2007, 17, 1412–1416. [Google Scholar] [CrossRef]
- Hama, T.; Takuda, H. Crystal-plasticity finite-element analysis of inelastic behavior during unloading in a magnesium alloy sheet. Int. J. Plast. 2011, 27, 1072–1092. [Google Scholar] [CrossRef] [Green Version]
- Hama, T.; Takuda, H. Crystal plasticity finite-element simulation of work-hardening behavior in a magnesium alloy sheet under biaxial tension. Comp. Mater. Sci. 2012, 51, 156–164. [Google Scholar] [CrossRef] [Green Version]
- Ritz, H.; Dawson, P.R. Sensitivity to grain discretization of the simulated crystal stress distributions in FCC polycrystals. Modell. Simul. in Mater. Sci. Eng. 2009, 17, 015001. [Google Scholar] [CrossRef]
- Pi, H.C.; Han, J.T.; Zhang, C.G.; Tieu, A.K.; Jiang, Z.Y. Modeling uniaxial tensile deformation of polycrystalline Al using CPFEM. J. Univ. Sci. Technol. Beijing 2008, 15, 43–47. [Google Scholar] [CrossRef]
- Nakamachi, E.; Tam, N.N.; Morimoto, H. Multi-scale finite element analyses of sheet metals by using SEM-EBSD measured crystallographic RVE models. Int. J. Plast. 2007, 23, 450–489. [Google Scholar] [CrossRef]
- Jigh, H.G.J.; Frsi, M.A.; Hosseini, T.H. Pre-diction of the stress–strain behavior of open-cell Aluminum foam under compressive loading and the effects of various RVE boundary conditions. J. Mater. Eng. Perform. 2018, 7, 2576–2585. [Google Scholar] [CrossRef]
- Zhang, L.; Jing, W.G.; Wu, Z.H. Finite element simulation on mechanical properties of hierarchical honeycombs. J. Nan-chang Hangkong Univ. (Nat. Sci.) 2016, 30, 22–27. [Google Scholar]
- Kamiński, M.; Sokołowski, D. Dual probabilistic homogenization of the rubber-based composite with random 373 carbon black particle reinforcement. Comp. Struct. 2016, 140, 783–797. [Google Scholar] [CrossRef]
- Rehrl, C.; Völker, B.; Kleber, S.; Antretter, T.; Pippan, R. Crystal orientation changes: A comparison between a crystal plasticity finite element study and experimental results. Acta Mater. 2003, 51, 2379–2386. [Google Scholar] [CrossRef]
- Smallman, R.E. Plasticity of crystals with special reference to metals by E. Schmid and W. Boas. J. Appl. Crystallogr. 2014, 25, 587–588. [Google Scholar]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. London A Math. Phys. Sci. 1976, 348, 101–127. [Google Scholar] [CrossRef]
- Wu, T.Y.; Bassani, J.L.; Laird, C. Latent hardening in single crystals I. theory and experiments. Proc. R. Soc. London A Math. Phys. Sci. 1991, 435, 1–19. [Google Scholar] [CrossRef]
- Bassani, J.L.; Wu, T.Y. Latent hardening in single crystals II. analytical characterization and predictions. Proc. R. Soc. London A Math. Phys. Sci. 1991, 435, 21–41. [Google Scholar] [CrossRef]
- Kysar, J.W. Addendum to a User-Material Subroutine Incorporating Single Crystal Plasticity in the ABAQUS Finite Element Program; Mech report 178; Division of Engineering and Applied Sciences, Harvard University: Cambridge, MA, USA, 1997. [Google Scholar]
- Simmons, G.; Wang, H. Single Crystal Elastic Constants and Calculated Polycrystal Properties; MIT Press: Cambridge, UK, 1971. [Google Scholar]
- Franciosi, P.; Berveiller, M.; Zaoui, A. Latent hardening in FCC crystals. In Strength of Metals and Alloys; Haasen, P., Gerold, V., Kostorz, G., Eds.; Elsevier Ltd.: Amsterdam, The Netherlands, 1979; Volume 1, pp. 23–28. [Google Scholar]
- Methods for Tension Testing of Metallic Foil; ASTM E345-08; American Society of Testing and Materials: West Conshohocken, PA, USA, 2016.
- Pan, W.K.; Wang, Z.Q.; Zhang, Y.W. Discrete slip model of crystal and finite element analysis. Acta mech. Sin. 1997, 29, 278–286. [Google Scholar]
- Zhang, C.; Zhang, L.W.; Shen, W.F.; Xia, Y.N.; Yan, Y.T. 3d crystal plasticity finite element modeling of the tensile deformation of polycrystalline ferritic stainless steel. Acta Metall. Sin. (Engl. Lett.) 2017, 30, 79–88. [Google Scholar] [CrossRef]
- Si, L.Y. Simulation of the Texture Evolution During Cold Deformation of FCC Metal with Crystal Plasticity FEM. Ph.D. Thesis, Northeastern University, Shengyang, China, June 2009. [Google Scholar]
- Chen, S.D.; Liu, X.H.; Liu, L.Z.; Song, M. Crystal plasticity finite element simulation of slip and deformation in ultra-thin Copper strip rolling. Acta Metall. Sin. 2016, 52, 120–128. [Google Scholar]













| 60 | 0.0001 | 245 | 30 | 74 | 105 | 0.001 | 1.0 |
| Number | Grain Orientation | Euler Angles | Miller Indices | Angle to X-Direction |
|---|---|---|---|---|
| No.1 | Brass | (35°, 45°, 90°) | (1 0 1) [] | 110.56° |
| No.2 | Copper | (90°, 35°, 45°) | (1 1 2) [] | 125.26° |
| No.3 | S | (61°, 34°, 64°) | (2 1 3) [] | 116.09° |
| No.4 | Cube | (0°, 0°, 0°) | (0 0 1) [] | 0° |
| No.5 | Goss | (0°, 45°, 90°) | (1 0 1) [] | 90° |
| Slip Plane | Slip Direction | Slip System | Slip Plane | Slip Direction | Slip System |
|---|---|---|---|---|---|
| () | [] | a1 | [] | c1 | |
| [] | a2 | () | [] | c2 | |
| [] | a3 | [] | c3 | ||
| () | [] | b1 | [] | d1 | |
| [] | b2 | () | [] | d2 | |
| [] | b3 | [] | d3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; Fan, W.; Hou, J.; Wang, T. A Numerical Study of Slip System Evolution in Ultra-Thin Stainless Steel Foil. Materials 2019, 12, 1819. https://doi.org/10.3390/ma12111819
Ren Z, Fan W, Hou J, Wang T. A Numerical Study of Slip System Evolution in Ultra-Thin Stainless Steel Foil. Materials. 2019; 12(11):1819. https://doi.org/10.3390/ma12111819
Chicago/Turabian StyleRen, Zhongkai, Wanwan Fan, Jie Hou, and Tao Wang. 2019. "A Numerical Study of Slip System Evolution in Ultra-Thin Stainless Steel Foil" Materials 12, no. 11: 1819. https://doi.org/10.3390/ma12111819
APA StyleRen, Z., Fan, W., Hou, J., & Wang, T. (2019). A Numerical Study of Slip System Evolution in Ultra-Thin Stainless Steel Foil. Materials, 12(11), 1819. https://doi.org/10.3390/ma12111819