An Examination of the Low Strain Rate Sensitivity of Additively Manufactured Polymer, Composite and Metallic Honeycomb Structures
Abstract
:1. Introduction
2. Materials and Methods
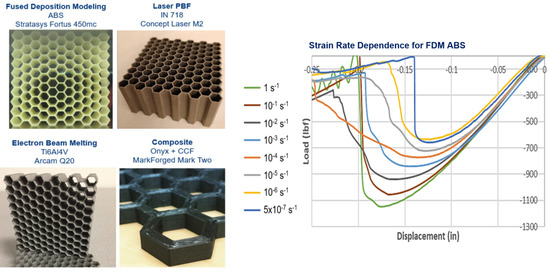
2.1. Fused Deposition Modeling with ABS
2.2. Composite Material Extrusion with Nylon-CF Composite and Continuous CF
2.3. Electron Beam Melting with Ti6Al4V
2.4. Laser Powder Bed Fusion with Inconel 718
3. Results
3.1. Fused Deposition Modeling with ABS
3.2. Composite Material Extrusion with Nylon-CF Composite and Continuous CF
3.3. Electron Beam Melting with Ti6Al4V
3.4. Laser Powder Bed Fusion with Inconel 718
3.5. Strain Rate Sensitivity
4. Discussion
5. Conclusions
- Polymer and composite honeycombs show evident strain rate dependence of the first maximum, or peak load. The magnitude of this dependence is process specific, but in general shows a difference of 10%–30% from the lowest to the highest strain rate. This dependence is less significant, but still present, for the effective modulus.
- Metallic honeycombs have no significant sensitivity to strain rate in regard to the effective modulus, but show some weak sensitivity to peak load.
Author Contributions
Funding
Conflicts of Interest
References
- Gibson, L.; Ashby, M. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Ashby, M.F.; Evans, A.G.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal Foams: A Design Guide; Butterworth Heinemann: Oxford, UK, 2000. [Google Scholar]
- Gibson, L.J.; Ashby, M.F.; Harley, B.A. Cellular Materials in Nature and Medicine, 1st ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bobbert, F.S.L.; Lietaert, K.; Eftekhari, A.A.; Pouran, B.; Ahmadi, S.M.; Weinans, H.; Zadpoor, A.A. Additively manufactured metallic porous biomaterials based on minimal surfaces: A unique combination of topological, mechanical, and mass transport properties. Acta Biomater. 2017, 53, 572–584. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhate, D. Design for Additive Manufacturing: Concepts and Considerations for the Aerospace Industry; SAE International: Warrendale, PA, USA, 2018. [Google Scholar]
- Sharma, R.; Le, T.; Song, J.; Harms, E.; Sowa, D.; Grishin, A.; Bhate, D. A Comparison of Modeling Methods for Predicting the Elastic-Plastic Response of Additively Manufactured Honeycomb Structures. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 13–15 August 2018. [Google Scholar]
- Dallago, M.; Raghavendra, S.; Luchin, V.; Zappini, G.; Pasini, D.; Benedetti, M. Geometric assessment of lattice materials built via Selective Laser Melting. Mater. Today Proc. 2019, 7, 353–361. [Google Scholar] [CrossRef]
- ISO. ISO 13314: Mechanical Testing of Metals, Ductility Testing, Compression Test for Porous and Cellular Metals; International Organization for Standardization: Geneva, Switzerland, 2011. [Google Scholar]
- Sun, Y.; Li, Q.M. Dynamic compressive behaviour of cellular materials: A review of phenomenon, mechanism and modelling. Int. J. Impact Eng. 2018, 112, 74–115. [Google Scholar] [CrossRef] [Green Version]
- Gümrük, R.; Mines, R.A.W.; Karadeniz, S. Determination of Strain Rate Sensitivity of Micro-struts Manufactured Using the Selective Laser Melting Method. J. Mater. Eng. Perform. 2018, 27, 1016–1032. [Google Scholar] [CrossRef]
- Santorinaios, M.; Brooks, W.; Sutcliffe, C.J.; Mines, R.A.W. Crush behaviour of open cellular lattice structures manufactured using selective laser melting. In WIT Transactions on the Built Environment; WIT Press: Southampton, UK, 2006. [Google Scholar] [CrossRef]
- Le, T.; Bhate, D.; Parsey, J.M.; Hsu, K.H. Determination of a Shape and Size Independent Material Modulus for Honeycomb Structures in Additive Manufacturing; In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2016.
- Yan, C.; Hao, L.; Hussein, A.; Raymont, D. Evaluations of cellular lattice structures manufactured using selective laser melting. Int. J. Mach. Tools Manuf. 2012, 62, 32–38. [Google Scholar] [CrossRef]
- Parthasarathy, J.; Starly, B.; Raman, S.; Christensen, A. Mechanical evaluation of porous titanium (Ti6Al4V) structures with electron beam melting (EBM). J. Mech. Behav. Biomed. Mater. 2010, 3, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Kucewicz, M.; Baranowski, P.; Małachowski, J.; Popławski, A.; Płatek, P. Modelling, and characterization of 3D printed cellular structures. Mater. Des. 2018, 142, 177–189. [Google Scholar] [CrossRef]
- Mazur, M.; Leary, M.; Sun, S.; Vcelka, M.; Shidid, D.; Brandt, M. Deformation and failure behaviour of Ti-6Al-4V lattice structures manufactured by selective laser melting (SLM). Int. J. Adv. Manuf. Technol. 2016, 84, 1391–1411. [Google Scholar] [CrossRef]
- Sadeghi, H.; Bhate, D.; Abraham, J.; Magallanes, J. Quasi-static and Dynamic Behavior of Additively Manufactured Metallic Lattice Cylinders. In Proceedings of the 20th Biennial Conference of the APS Topical Group on Shock Compression Condensed Matter, St. Louis, MO, USA, 9–14 July 2017. [Google Scholar] [CrossRef]
- Harris, J.A.; Winter, R.E.; McShane, G.J. Impact response of additively manufactured metallic hybrid lattice materials. Int. J. Impact Eng. 2017, 104, 177–191. [Google Scholar] [CrossRef] [Green Version]
- Vairis, A.; Petousis, M.; Vidakis, N.; Savvakis, K. On the Strain Rate Sensitivity of Abs and Abs Plus Fused Deposition Modeling Parts. J. Mater. Eng. Perform. 2016, 25, 3558–3565. [Google Scholar] [CrossRef]
- Andrews, E.W.; Gioux, G.; Onck, P.; Gibson, L.J. Size effects in ductile cellular solids. Part II: Experimental results. Int. J. Mech. Sci. 2001, 43, 701–713. [Google Scholar] [CrossRef]
- Tekoglu, C.; Gibson, L.J.; Pardoen, T.; Onck, P.R. Size effects in foams: Experiments and modeling. Prog. Mater. Sci. 2011, 56, 109–138. [Google Scholar] [CrossRef]
- Liu, Y.D.; Yu, J.L.; Zheng, Z.J.; Li, J.R. A numerical study on the rate sensitivity of cellular metals. Int. J. Solids Struct. 2009, 46, 3988–3998. [Google Scholar] [CrossRef] [Green Version]















| Process | Equipment | Material | Layer Thickness |
|---|---|---|---|
| Fused Deposition Modeling | Stratasys 450mc | ABS-M30TM | 250 µm |
| Fiber Composite Printing | MarkForged Mark Two | OnyxTM and Continuous Carbon Fiber | 100 µm |
| Electron Beam Melting | Arcam Q20 | Ti6Al4V | proprietary |
| Laser Powder Bed Fusion | Concept Laser M2 | Inconel 718 | 40 µm |
| Process/Material | Strain Rate Sensitivity of E* (m) | R2 (Quality of Fit) |
|---|---|---|
| FDM /ABS | 0.0219 | 0.9535 |
| Composite/Carbon Fiber | 0.0129 | 0.7892 |
| EBM/Ti6Al4V | 0.0005 | 0.0056 |
| LPBF/Inconel 718 | 0.0108 | 0.1303 |
| Process/Material | Strain Rate Sensitivity of σ* (n) | R2 (Quality of Fit) |
|---|---|---|
| FDM /ABS | 0.0405 | 0.9902 |
| Composite/Carbon Fiber | 0.0369 | 0.9561 |
| EBM/Ti6Al4V | 0.0155 | 0.5839 |
| LPBF/Inconel 718 | 0.0042 | 0.5615 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lam, Q.; Patil, D.; Le, T.; Eppley, T.; Salti, Z.; Goss, D.; Grishin, A.; Bhate, D. An Examination of the Low Strain Rate Sensitivity of Additively Manufactured Polymer, Composite and Metallic Honeycomb Structures. Materials 2019, 12, 3455. https://doi.org/10.3390/ma12203455
Lam Q, Patil D, Le T, Eppley T, Salti Z, Goss D, Grishin A, Bhate D. An Examination of the Low Strain Rate Sensitivity of Additively Manufactured Polymer, Composite and Metallic Honeycomb Structures. Materials. 2019; 12(20):3455. https://doi.org/10.3390/ma12203455
Chicago/Turabian StyleLam, Quoc, Dhiraj Patil, Thao Le, Trevor Eppley, Ziyad Salti, Derek Goss, Alex Grishin, and Dhruv Bhate. 2019. "An Examination of the Low Strain Rate Sensitivity of Additively Manufactured Polymer, Composite and Metallic Honeycomb Structures" Materials 12, no. 20: 3455. https://doi.org/10.3390/ma12203455
APA StyleLam, Q., Patil, D., Le, T., Eppley, T., Salti, Z., Goss, D., Grishin, A., & Bhate, D. (2019). An Examination of the Low Strain Rate Sensitivity of Additively Manufactured Polymer, Composite and Metallic Honeycomb Structures. Materials, 12(20), 3455. https://doi.org/10.3390/ma12203455