Deformation-Assisted Joining of Sheets to Tubes by Annular Sheet Squeezing
Abstract
:1. Introduction
- (i)
- (ii)
- (iii)
2. Materials and Methods
2.1. Materials and Flow Curves
2.2. Experimental Tests
- The tube and the sheet were first cut to the required sizes;
- A hole with a diameter equal to the outer tube diameter was drilled in the sheet;
- The tube and the sheet were then placed in the tooling system installed in a hydraulic testing machine INSTRON SATEC 1200 kN;
- The hydraulic testing machine moved the punch downwards in order to locally compress the sheet up to a total squeezing depth
- Steps 1 to 4 were repeated several times in order to vary the sheet thickness ts, the cross-section recess length of the punch, and the squeezing depth d according to the values listed in Table 1. All the tests were performed at room temperature;
- After finishing the tests, selected samples were cut along their axial cross-sectional planes in order to analyze their mechanical form-fit joints, to take photographs, and to perform measurements;
- Finally, another set of selected samples was subjected to destructive pull-out tests in order to evaluate the overall performance of the joints.
2.3. Finite Element Modelling
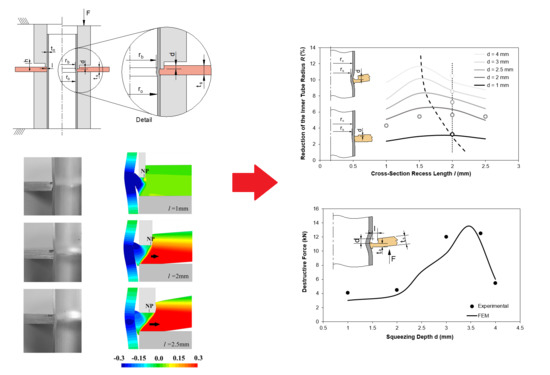
3. Results
4. Discussion
4.1. Pull-Out Destructive Forces
4.2. Sheet Thickness
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, C.; Zhao, S.; Han, X.; Zhao, X.; Ishida, T. Experimental investigation on the joining of aluminum alloy sheets using improved clinching process. Materials 2017, 10, 887. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhao, S.; Han, X.; Wang, Y.; Zhao, X. Investigation of flat clinching process combined with material forming technology for aluminum alloy. Materials 2017, 10, 1433. [Google Scholar] [CrossRef] [PubMed]
- Jäckel, M.; Grimm, T.; Niegsch, R.; Drossel, W.G. Overview of current challenges in self-pierce riveting of lightweight materials. Proceedings 2018, 3, 384. [Google Scholar] [CrossRef]
- Silva, D.F.M.; Silva, C.M.A.; Bragança, I.M.F.; Nielsen, C.V.; Alves, L.M.; Martins, P.A.F. On the performance of thin-walled crash boxes joined by forming. Materials 2018, 11, 1118. [Google Scholar] [CrossRef] [PubMed]
- Marre, M.; Rautenberg, J.; Tekkaya, A.E.; Zabel, A.; Biermann, D.; Wojciechowski, J.; Przybylski, W. An experimental study on the groove design for joints produced by hydraulic expansion considering axial or torque load. Mater. Manuf. Process. 2012, 27, 545–555. [Google Scholar] [CrossRef]
- Psyk, V.; Risch, D.; Kinsey, B.L.; Tekkaya, A.E.; Kleiner, M. Electromagnetic forming-A review. J. Mater. Process. Technol. 2011, 211, 787–829. [Google Scholar] [CrossRef]
- Serio, L.M.; Palumbo, D.; Filippis, L.A.C.D.; Galietti, U.; Ludovico, A.D. Effect of friction stir process parameters on the mechanical and thermal behavior of 5754-H111 aluminum plates. Materials 2016, 9, 122. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, X.; Pan, K.; Wang, J. Multi-objective optimization of friction stir spot-welded parameters on aluminum alloy sheets based on automotive joint loads. Metals 2019, 9, 520. [Google Scholar] [CrossRef]
- Mahmood, Y.; Dai, K.; Chen, P.; Zhou, Q.; Bhatti, A.A.; Arab, A. Experimental and numerical study on microstructure and mechanical properties of Ti-6Al-4V/Al-1060 Explosive Welding. Metals 2019, 9, 1189. [Google Scholar] [CrossRef]
- Cortés, V.H.V.; Guerrero, G.A.; Granados, I.M.; Hernández, V.H.B.; Zepeda, C.M. Effect of retained austenite and non-metallic inclusions on the mechanical properties of resistance spot welding nuggets of low-alloy TRIP steels. Metals 2019, 9, 1064. [Google Scholar] [CrossRef]
- Lim, Y.C.; Park, H.; Jang, J.; McMurray, J.W.; Lokitz, B.S.; Keum, J.K.; Wu, Z.; Feng, Z. Dissimilar materials joining of carbon fiber polymer to dual phase 980 by friction bit joining, adhesive bonding, and weldbonding. Metals 2018, 8, 865. [Google Scholar] [CrossRef]
- Mori, K.; Bay, N.; Fratini, L.; Micari, F.; Tekkaya, A.E. Joining by plastic deformation. CIRP Ann. Manuf. Technol. 2013, 62, 673–694. [Google Scholar] [CrossRef]
- Groche, P.; Wohletz, S.; Brenneis, M.; Pabst, C.; Resch, F. Joining by forming-A review on joint mechanisms, applications and future trends. J. Mater. Process. Technol. 2014, 214, 1972–1994. [Google Scholar] [CrossRef]
- Alves, L.M.; Dias, E.J.; Martins, P.A.F. Joining sheet panels to thin-walled tubular profiles by tube end forming. J. Clean. Prod. 2011, 19, 712–719. [Google Scholar] [CrossRef]
- Alves, L.M.; Martins, P.A.F. Single-stroke mechanical joining of sheet panels to tubular profiles. J. Manuf. Process. 2013, 15, 151–157. [Google Scholar] [CrossRef]
- Alves, L.M.; Afonso, R.M.; Silva, C.M.A.; Martins, P.A.F. Joining tubes to sheets by boss forming and upsetting. J. Mater. Process. Technol. 2018, 252, 773–781. [Google Scholar] [CrossRef]
- Alves, L.M.; Afonso, R.M.; Silva, C.M.A.; Martins, P.A.F. Joining sandwich composite panels to tubes. J. Mater. Des. Appl. 2019, 233, 1472–1481. [Google Scholar] [CrossRef]
- Hao, J.W.; Pan, H.L.; Tang, S.H. Research of elastomeric expansion for tube-to-tubesheet joint. In Proceedings of the ASME Pressure Vessels and Piping Division Conference, Vancouver, BC, Canada, 23–27 July 2006; pp. 1–5. [Google Scholar]
- Wrobel, N.; Rejek, M.; Krolczyk, G.; Hloch, S. Testing of Tight Crimped Joint Made on a Prototype Stand; Advances in Manufacturing, Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2017; pp. 497–507. ISBN 978-3-319-68619-6. [Google Scholar]
- Rejek, M.; Wróbel, N.; Królczyk, J.; Królczyk, G. Designing and testing cold-formed rounded connections made on a prototype station. Materials 2019, 12, 1061. [Google Scholar] [CrossRef]
- Sizova, I.; Sviridov, A.; Bambach, M. Avoiding crack nucleation and propagation during upset bulging of tubes. Int. J. Mater. Form. 2017, 10, 443–451. [Google Scholar] [CrossRef]
- Alves, L.M.; Silva, F.L.R.; Afonso, R.M.; Martins, P.A.F. Joining sheets to tubes by annular sheet squeezing. Int. J. Mach. Tools Manuf. 2019, 143, 16–22. [Google Scholar] [CrossRef]
- Alves, L.M.; Nielsen, C.V.; Martins, P.A.F. Revisiting the fundamentals and capabilities of the stack compression test. Exp. Mech. 2011, 51, 1565–1572. [Google Scholar] [CrossRef]
- Alves, L.M.; Silva, F.L.R.; Afonso, R.M.; Martins, P.A.F. A new joining by forming process for fixing sheets to tubes. Int. J. Adv. Manuf. Technol. 2019, 104, 3199–3207. [Google Scholar] [CrossRef]
- Tekkaya, A.E.; Martins, P.A.F. Accuracy, reliability and validity of finite element analysis in metal forming: A user’s perspective. Eng. Comput. 2009, 26, 1026–1055. [Google Scholar] [CrossRef]
- Markov, A.A. On variational principles in theory of plasticity. Prikl. Mat. Mek. 1947, II, 339–350. [Google Scholar]
- Nielsen, C.V.; Zhang, W.; Alves, L.M.; Bay, N.; Martins, P.A.F. Modelling of Thermo-Electro-Mechanical Manufacturing Processes with Applications in Metal Forming and Resistance Welding; Springer: London, UK, 2013; ISBN 978-1-4471-4643-8. [Google Scholar]










| r0 (mm) | t0 (mm) | ts (mm) | l (mm) | d (mm) |
|---|---|---|---|---|
| 14.5 | 1.5 | 2.5, 5 | 0.5–2.5 | 1.0–4.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alves, L.M.; Afonso, R.M.; Silva, F.L.R.; Martins, P.A.F. Deformation-Assisted Joining of Sheets to Tubes by Annular Sheet Squeezing. Materials 2019, 12, 3909. https://doi.org/10.3390/ma12233909
Alves LM, Afonso RM, Silva FLR, Martins PAF. Deformation-Assisted Joining of Sheets to Tubes by Annular Sheet Squeezing. Materials. 2019; 12(23):3909. https://doi.org/10.3390/ma12233909
Chicago/Turabian StyleAlves, Luis M., Rafael M. Afonso, Frederico L.R. Silva, and Paulo A.F. Martins. 2019. "Deformation-Assisted Joining of Sheets to Tubes by Annular Sheet Squeezing" Materials 12, no. 23: 3909. https://doi.org/10.3390/ma12233909
APA StyleAlves, L. M., Afonso, R. M., Silva, F. L. R., & Martins, P. A. F. (2019). Deformation-Assisted Joining of Sheets to Tubes by Annular Sheet Squeezing. Materials, 12(23), 3909. https://doi.org/10.3390/ma12233909