Numerical Assessment on Rotation Effect of the Stagnation Surface on Nanoparticle Deposition in Flame Synthesis
Abstract
:1. Introduction
2. Numerical Methods
3. Results and Discussions
3.1. Axial Velocity Contours at Different Rotational Speeds
3.2. Temperature Fields at Different Rotational Speeds
3.3. Particle Deposition Trajectory at Different Rotational Speeds
3.4. Particle Deposition Time at Different Rotational Speeds
3.5. Particle Deposition Temperature at Different Rotational Speeds
3.6. Particle Deposition O2 Concentration at Different Rotational Speeds
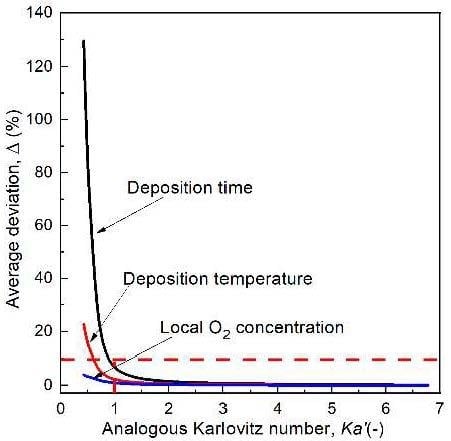
3.7. The Effect of the Tangential Velocity and Flame Stretch Rate
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, Y.; Yoon, Y.; Shin, D. Fabrication of Sn/SnO2 composite powder for anode of lithium ion battery by aerosol flame deposition. J. Anal. Appl. Pyrolysis 2009, 85, 557–560. [Google Scholar] [CrossRef]
- Jensen, J.R.; Johannessen, T.; Wedel, S.; Livbjerg, H. A study of Cu/ZnO/Al2O3 methanol catalysts prepared by flame combustion synthesis. J. Catalysis 2003, 218, 67–77. [Google Scholar] [CrossRef]
- Akpan, U.G.; Hameed, B.H. Parameters affecting the photocatalytic degradation of dyes using TiO2-based photocatalysts: A review. J. Hazard. Mater. 2009, 170, 520–529. [Google Scholar] [CrossRef] [PubMed]
- Kulal, A.B.; Dongare, M.K.; Umbarkar, S.B. Sol-gel synthesized WO3 nanoparticles supported on mesoporous silica for liquid phase nitration of aromatics. Appl. Catal. B Environ. 2016, 182, 142–152. [Google Scholar] [CrossRef]
- Habibi, M.H.; Mardani, M. Co-precipitation synthesis of nano-composites consists of zinc and tin oxides coatings on glass with enhanced photocatalytic activity on degradation of reactive blue 160 KE2B. Spectrochim. Acta A 2015, 137, 785–789. [Google Scholar] [CrossRef]
- Liu, J.L.; Fan, L.Z.; Qu, X.H. Low temperature hydrothermal synthesis of nano-sized manganese oxide for supercapacitors. Electrochim. Acta 2012, 66, 302–305. [Google Scholar] [CrossRef]
- Feng, D.Y.; Rui, Z.B.; Lu, Y.B.; Ji, H.B. A simple method to decorate TiO2 nanotube arrays with controllable quantity of metal nanoparticles. Chem. Eng. J. 2012, 179, 363–371. [Google Scholar] [CrossRef]
- Lu, Y.B.; Wang, J.M.; Yu, L.; Kovarik, L.; Zhang, X.W.; Hoffman, A.S.; Gallo, A.; Bare, S.R.; Sokaras, D.; Kroll, T.; et al. Identification of the active complex for CO oxidation over single-atom Ir-on-MgAl2O4 catalysts. Nat. Catal. 2019, 2, 149–156. [Google Scholar] [CrossRef]
- Mozaffari, S.; Li, W.H.; Thompson, C.; Ivanov, S.; Seifert, S.; Lee, B.; Kovarik, L.; Karim, A.M. Colloidal nanoparticle size control: Experimental and kinetic modeling investigation of the ligand-metal binding role in controlling the nucleation and growth kinetics. Nanoscale 2017, 9, 13772–13785. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Li, S.Q.; Deng, S.L.; Yao, Q.; Tse, D.S. Direct synthesis of nanostructured TiO2 films with controlled morphologies by stagnation swirl flames. J. Aerosol Sci. 2012, 44, 71–82. [Google Scholar] [CrossRef]
- Wooldridge, M.S. Gas-phase combustion synthesis of particles. Prog. Energy Comb. Sci. 1998, 24, 63–87. [Google Scholar] [CrossRef]
- Pratsinis, S.E. Flame aerosol synthesis of ceramic powders. Prog. Energy Comb. Sci. 1998, 24, 197–219. [Google Scholar] [CrossRef]
- Yue, R.L.; Dong, M.; Ni, Y.; Jia, Y.; Liu, G.; Yang, J.; Liu, H.D.; Wu, X.F.; Chen, Y.F. One-step flame synthesis of hydrophobic silica nanoparticles. Powder Technol. 2013, 235, 909–913. [Google Scholar] [CrossRef]
- Memarzadeh, S.; Tolmachoff, E.D.; Phares, D.J.; Wang, H. Properties of nanocrystalline TiO2 synthesized in premixed flames stabilized on a rotating surface. Proc. Combust. Inst. 2011, 33, 1917–1924. [Google Scholar] [CrossRef]
- Gutsch, A.; Mühlenweg, H.; Krämer, M. Tailor-made nanoparticles via gas-phase synthesis. Small 2005, 1, 30–46. [Google Scholar] [CrossRef] [PubMed]
- Tolmachoff, E.D.; Abid, A.D.; Phares, D.J.; Campbell, C.S.; Wang, H. Proc. Synthesis of nano-phase TiO2 crystalline films over premixed stagnation flames. Combust. Inst. 2009, 32, 1839–1845. [Google Scholar] [CrossRef]
- Nikraz, S.; Wang, H. Dye sensitized solar cells prepared by flames stabilized on a rotating surface. Proc. Combust. Inst. 2013, 34, 2171–2178. [Google Scholar] [CrossRef]
- Miao, Z.; Zhang, Y.; Zhang, H.; Liu, Q.; Yang, H.R. Experimental study on gas sensing properties of TiO2 film produced by flame synthesis. In Proceedings of the China National Symposium on Combustion, Xi’an, China, 31 October–2 November 2014. [Google Scholar]
- Tolmachoff, E.D.; Memarzadeh, S.; Wang, H. Nanoporous titania gas sensor films prepared in a premixed stagnation flame. J. Phys. Chem. C 2011, 115, 21620–21628. [Google Scholar] [CrossRef]
- Mädler, L.; Roessler, A.; Pratsinis, S.E.; Sahm, T.; Gurlo, A.; Barsan, N.; Weimar, U. Direct formation of highly porous gas-sensing films by in situ thermophoretic deposition of flame-made Pt/SnO2 nanoparticles. Sensor Actuat. B-Chem. 2006, 114, 283–295. [Google Scholar] [CrossRef]
- Wang, Y.; He, Y.M.; Lai, Q.H.; Fan, M.H. Review of the progress in preparing nano TiO2: An important environmental engineering material. J. Environ. Sci. 2014, 26, 2139–2177. [Google Scholar] [CrossRef] [PubMed]
- Westbrook, C.K.; Dryer, F.L. Simplified Reaction Mechanisms for the Oxidation of Hydrocarbon Fuel in Flames. Comb. Sci. Tech. 1981, 27, 31–43. [Google Scholar] [CrossRef]
- Wang, H.; You, X.; Joshi, A.V.; Davis, S.G.; Laskin, A.; Egolfopoulos, F.N.; Law, C.K. High-Temperature Combustion Reaction Model of H2/CO/C1-C4 Compounds. Available online: http://ignis.usc.edu/USC_Mech_II.htm (accessed on 18 April 2019).
- Waldmann, L.; Schmitt, K.H. Thermophoresis and diffusiophoresis of aerosol. In Aerosol Science; Academic Press: London, UK, 1966; pp. 137–162. [Google Scholar]
- Friedlander, S.K. Smoke, Dust and Haze: Fundamentals of Aerosol Dynamics, 2nd ed.; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Zhao, B.; Uchikawa, K.; Mccormick, J.R.; Ni, C.Y.; Chen, J.G.; Wang, H. Ultrafine anatase TiO2 nanoparticles produced in premixed ethylene stagnation flame at 1 atm. Proc. Combust. Inst. 2005, 30, 2569–2576. [Google Scholar] [CrossRef]
- Law, C.K. Combustion Physics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Taamallah, S.; Shanbhogue, S.J.; Ghoniem, A.F. Turbulent flame stabilization modes in premixed swirl combustion: Physical mechanism and Karlovitz number-based criterion. Combust. Flame 2016, 166, 19–33. [Google Scholar] [CrossRef]















© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, L.; Miao, Z.; Zhang, Y.; Zhang, H.; Yang, H. Numerical Assessment on Rotation Effect of the Stagnation Surface on Nanoparticle Deposition in Flame Synthesis. Materials 2019, 12, 1361. https://doi.org/10.3390/ma12091361
Hu L, Miao Z, Zhang Y, Zhang H, Yang H. Numerical Assessment on Rotation Effect of the Stagnation Surface on Nanoparticle Deposition in Flame Synthesis. Materials. 2019; 12(9):1361. https://doi.org/10.3390/ma12091361
Chicago/Turabian StyleHu, Lilin, Zhu Miao, Yang Zhang, Hai Zhang, and Hairui Yang. 2019. "Numerical Assessment on Rotation Effect of the Stagnation Surface on Nanoparticle Deposition in Flame Synthesis" Materials 12, no. 9: 1361. https://doi.org/10.3390/ma12091361
APA StyleHu, L., Miao, Z., Zhang, Y., Zhang, H., & Yang, H. (2019). Numerical Assessment on Rotation Effect of the Stagnation Surface on Nanoparticle Deposition in Flame Synthesis. Materials, 12(9), 1361. https://doi.org/10.3390/ma12091361