First-Principles Calculations of Oxygen-Dislocation Interaction in Magnesium
Abstract
:1. Introduction
2. Computational Method
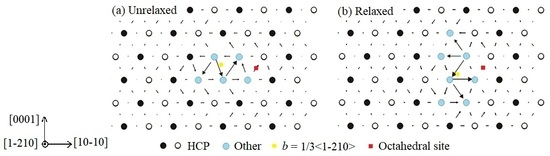
3. Results and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Data Availability
References
- Pollock, T.M. Weight Loss with Magnesium Alloys. Science 2010, 328, 986–987. [Google Scholar] [CrossRef]
- Agnew, S.R.; Nie, J.F. Preface to the Viewpoint Set On: The Current State of Magnesium Alloy Science and Technology. Scr. Mater. 2010, 63, 671–673. [Google Scholar] [CrossRef]
- Wu, Z.; Curtin, W.A. The Origins of High Hardening and Low Ductility in Magnesium. Nature 2015, 526, 62–67. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Z.; Ahmad, R.; Yin, B.; Sandlöbes, S.; Curtin, W.A. Mechanistic Origin and Prediction of Enhanced Ductility in Magnesium Alloys. Science 2018, 359, 447–452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Majd, A.M.; Farzinfar, M.; Pashakhanlou, M.; Nayyeri, M.J. Effect of RE Elements On the Microstructural and Mechanical Properties of As-Cast and Age Hardening Processed Mg–4Al–2Sn Alloy. J. Magnes. Alloys 2018, 6, 309–317. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, S.; Wu, R.; Hou, L.; Zhang, M. Recent Developments in High-Strength Mg-RE-based Alloys: Focusing On Mg-Gd and Mg-Y Systems. J. Magnes. Alloys 2018, 6, 277–291. [Google Scholar] [CrossRef]
- Zhang, J.; Dou, Y.; Dong, H. Intrinsic Ductility of Mg-based Binary Alloys: A First-Principles Study. Scr. Mater. 2014, 89, 13–16. [Google Scholar] [CrossRef]
- Ventelon, L.; Lüthi, B.; Clouet, E.; Proville, L.; Legrand, B.; Rodney, D.; Willaime, F. Dislocation Core Reconstruction Induced by Carbon Segregation in Bcc Iron. Phys. Rev. B 2015, 91, 220102. [Google Scholar] [CrossRef] [Green Version]
- Chaari, N.; Rodney, D.; Clouet, E. Oxygen—Dislocation Interaction in Titanium from First Principles. Scr. Mater. 2019, 162, 200–203. [Google Scholar] [CrossRef] [Green Version]
- Chaari, N.; Rodney, D.; Clouet, E. Oxygen—Dislocation Interaction in Zirconium from First Principles. Acta Mater. 2017, 132, 416–424. [Google Scholar] [CrossRef] [Green Version]
- Yu, Q.; Qi, L.; Tsuru, T.; Traylor, R.; Rugg, D.; Morris, J.W.; Asta, M.; Chrzan, D.C.; Minor, A.M. Origin of Dramatic Oxygen Solute Strengthening Effect in Titanium. Science 2015, 347, 635–639. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, H.; Choi, H.J.; Kang, S.W.; Shin, S.E.; Choi, G.S.; Bae, D.H. Multi-Functional Magnesium Alloys Containing Interstitial Oxygen Atoms. Sci. Rep. 2016, 6, 23184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, X.; Liu, L.; Wang, R.; Gan, L.; Liu, Q. Energy Investigations On the Mechanical Properties of Magnesium Alloyed by X = C, B, N, O and Vacancy. Front. Mater. Sci. 2013, 7, 405–412. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, G.; Wei, X. Strengthening and Ductilization Potentials of Nonmetallic Solutes in Magnesium: First-Principles Calculation of Generalized Stacking Fault Energies. Mater. Lett. 2015, 150, 111–113. [Google Scholar] [CrossRef]
- Rice, J.R. Dislocation Nucleation from a Crack Tip: An Analysis Based On the Peierls Concept. J. Mech. Phys. Solids 1992, 40, 239–271. [Google Scholar] [CrossRef]
- Clouet, E. Screw Dislocation in Zirconium: An Ab Initio Study. Phys. Rev. B 2012, 86, 144104. [Google Scholar] [CrossRef] [Green Version]
- Chaari, N.; Clouet, E.; Rodney, D. First-Principles Study of Secondary Slip in Zirconium. Phys. Rev. Lett. 2014, 112, 075504. [Google Scholar] [CrossRef] [Green Version]
- Fang, C.; Zhang, J.; Pan, F. First-Principles Study On Solute-Basal Dislocation Interaction in Mg Alloys. J. Alloys Compd. 2019, 785, 911–917. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A Tool for Manipulating and Converting Atomic Data Files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Kwasniak, P.; Garbacz, H. Screw Dislocation Mediated Solution Strengthening of Substitutional α-Ti Alloys—First Principles Investigation. Acta Mater. 2017, 141, 405–418. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated Identification and Indexing of Dislocations in Crystal Interfaces. Model. Simul. Mater. Sci. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO–The Open Visualization Tool. Model. Simul. Mater. Sci. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Liang, M.H.; Bacon, D.J. Computer Simulation of Dislocation Cores in H.C.P. Metals II. Core Structure in Unstressed Crystals. Philos. Mag. A 1986, 53, 181–204. [Google Scholar] [CrossRef]
- Vítek, V.; Perrin, R.C.; Bowen, D.K. The Core Structure of ½ (111) Screw Dislocations in B.C.C. Crystals. Philos. Mag. 1970, 21, 1049–1073. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Yasi, J.A.; Nogaret, T.; Trinkle, D.R.; Qi, Y.; Hector, L.G., Jr.; Curtin, W.A. Basal and Prism Dislocation Cores in Magnesium: Comparison of First-Principles and Embedded-Atom-Potential Methods Predictions. Model. Simul. Mater. Sci. 2009, 17, 055012. [Google Scholar] [CrossRef] [Green Version]
- Wakeda, M.; Tsuru, T.; Kohyama, M.; Ozaki, T.; Sawada, H.; Itakura, M.; Ogata, S. Chemical Misfit Origin of Solute Strengthening in Iron Alloys. Acta Mater. 2017, 131, 445–456. [Google Scholar] [CrossRef]
- Barkia, B.; Couzinié, J.P.; Lartigue-Korinek, S.; Guillot, I.; Doquet, V. In Situ TEM Observations of Dislocation Dynamics in Α Titanium: Effect of the Oxygen Content. Mater. Sci. Eng. A 2017, 703, 331–339. [Google Scholar] [CrossRef]
- Soo, P.; Higgins, G.T. The Deformation of Zirconium-Oxygen Single Crystals. Acta Metall. 1968, 16, 177–186. [Google Scholar] [CrossRef]
- Akhtar, A.; Teghtsoonian, A. Plastic Deformation of Zirconium Single Crystals. Acta Metall. 1971, 19, 655–663. [Google Scholar] [CrossRef]
- Tsuru, T.; Chrzan, D.C. Effect of Solute Atoms On Dislocation Motion in Mg: An Electronic Structure Perspective. Sci. Rep. 2015, 5, 8793. [Google Scholar] [CrossRef] [PubMed] [Green Version]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, C.; Zhang, J.; Huang, Y.; Chen, J. First-Principles Calculations of Oxygen-Dislocation Interaction in Magnesium. Materials 2020, 13, 116. https://doi.org/10.3390/ma13010116
Fang C, Zhang J, Huang Y, Chen J. First-Principles Calculations of Oxygen-Dislocation Interaction in Magnesium. Materials. 2020; 13(1):116. https://doi.org/10.3390/ma13010116
Chicago/Turabian StyleFang, Chao, Jing Zhang, Ying Huang, and Jianhao Chen. 2020. "First-Principles Calculations of Oxygen-Dislocation Interaction in Magnesium" Materials 13, no. 1: 116. https://doi.org/10.3390/ma13010116
APA StyleFang, C., Zhang, J., Huang, Y., & Chen, J. (2020). First-Principles Calculations of Oxygen-Dislocation Interaction in Magnesium. Materials, 13(1), 116. https://doi.org/10.3390/ma13010116