Modified Biopolymer Adsorbents for Column Treatment of Sulfate Species in Saline Aquifers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Experimental Methods
2.2.1. Preparation of Adsorbents
2.2.2. Characterization
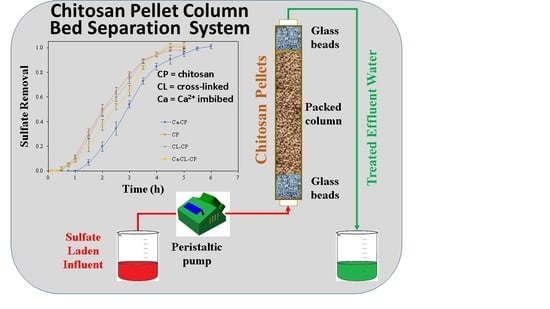
2.2.3. Dynamic Adsorption Tests
3. Result and Discussion
3.1. Functional Groups on Adsorbents
3.2. Thermal Stability
3.3. Breakthrough Parameters for the Sulfate Adsorption Isotherms
3.4. Kinetic Models for Sulfate Adsorption in the Continuous Fixed-Bed Column
3.4.1. Thomas Model
3.4.2. Yoon–Nelson Model
3.5. Effect of Operating Conditions on Column Efficiency
3.5.1. Bed Height
3.5.2. Initial Sulfate Concentration
3.5.3. Flow Rate
3.6. Dynamic Modeling of Sulfate Adsorption in Ca–CP Pellets Using the Thomas Model
3.6.1. Effect of Bed Height
3.6.2. Effect of Initial Sulfate Concentration
3.6.3. Effect of Flow Rate
3.7. Desorption Study
4. Conclusions
- Increased bed height resulted in greater adsorption capacity and sulfate removal;
- Greater flow rate (3 vs. 5 mL/min) led to increased maximum adsorption capacity (qmax) but decreased sulfate removal (%), where premature sulfate breakthrough resulted at higher flow rate under such dynamic adsorption conditions;
- Greater intial sulfate concentration from 1000 to 2000 mg/L enhanced the driving force for mass transfer, that contributed to an increased maximum adsorption capacity;
- Sulfate adsorption onto Ca–CP adsorbent at variable operating parameters was well represented by the Thomas model; and
- The desorption experiments with 0.5 M NaCl showed good performance of Ca–CP over the first 2 cycles, whereas a decrease was evident for further cycles.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shinde, B.; Sayed, K.; Nandolia, D.; Mishra, M. Groundwater quality analysis in part of Bagalkot and Bilagi area. SSRN Electron. J. 2020, 6, 306–310. [Google Scholar] [CrossRef]
- Jakóbczyk-Karpierz, S.; Sitek, S.; Jakobsen, R.; Kowalczyk, A. Geochemical and isotopic study to determine sources and processes affecting nitrate and sulphate in groundwater influenced by intensive human activity—Carbonate aquifer Gliwice (southern Poland). Appl. Geochem. 2017, 76, 168–181. [Google Scholar] [CrossRef]
- Thompson, T.S. General chemical water quality of private groundwater supplies in Saskatchewan, Canada. Bull. Environ. Contam. Toxicol. 2003, 70, 447–454. [Google Scholar] [CrossRef]
- Burgess, B.A.; Lohmann, K.L.; Blakley, B.R. Excessive sulfate and poor water quality as a cause of sudden deaths and an outbreak of diarrhea in horses. Can. Vet. J. 2010, 51, 277–282. [Google Scholar] [PubMed]
- Feist, M.; Elford, C.; Bailey, P.; Campbell, J. A Review of Dugout and Well Water Tested for Livestock Quality in Southern Saskatchewan; Western College of Veterinary Medicine: Saskatoon, SK, Canada; Government of Saskatchewan: Saskatoon, SK, Canada, 2017; pp. 1–27.
- Health Canada. Guidelines for Canadian Drinking Water Quality—Summary Table; Water and Air Quality Bureau, Healthy Environments and Consumer Safety Branch, Health Canada: Ottawa, ON, Canada, 2009.
- Runtti, H.; Tolonen, E.T.; Tuomikoski, S.; Luukkonen, T.; Lassi, U. How to tackle the stringent sulfate removal requirements in mine water treatment—A review of potential methods. Environ. Res. 2018, 167, 207–222. [Google Scholar] [CrossRef]
- Silva, R.; Cadorin, L.; Rubio, J. Sulphate ions removal from an aqueous solution: I. Co-Precipitation with hydrolysed aluminum-bearing salts. Miner. Eng. 2010, 23, 1220–1226. [Google Scholar] [CrossRef]
- Foudhaili, T.; Lefebvre, O.; Coudert, L.; Neculita, C.M. Sulfate removal from mine drainage by electrocoagulation as a stand-alone treatment or polishing step. Miner. Eng. 2020, 152, 106337. [Google Scholar] [CrossRef]
- Najib, T.; Solgi, M.; Farazmand, A.; Heydarian, S.M.; Nasernejad, B. Optimization of sulfate removal by sulfate reducing bacteria using response surface methodology and heavy metal removal in a sulfidogenic UASB reactor. J. Environ. Chem. Eng. 2017, 5, 3256–3265. [Google Scholar] [CrossRef]
- Gogoi, H.; Leiviskä, T.; Rämö, J.; Tanskanen, J. Production of aminated peat from branched polyethylenimine and glycidyltrimethylammonium chloride for sulphate removal from mining water. Environ. Res. 2019, 175, 323–334. [Google Scholar] [CrossRef]
- Ao, H.; Cao, W.; Hong, Y.; Wu, J.; Wei, L. Adsorption of sulfate ion from water by zirconium oxide-modified biochar derived from pomelo peel. Sci. Total Environ. 2020, 708, 135092. [Google Scholar] [CrossRef]
- Vafakish, B.; Wilson, L.D. Cu (II) Ion adsorption by Aniline grafted Chitosan and its responsive fluorescence properties. Molecules 2020, 25, 1052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dotto, G.L.; Mckay, G. Current scenario and challenges in adsorption for water treatment. J. Environ. Chem. Eng. 2020, 8, 103988. [Google Scholar] [CrossRef]
- Mahaninia, M.H.; Wilson, L.D. Phosphate uptake studies of cross-linked chitosan bead materials. J. Colloid Interface Sci. 2017, 485, 201–212. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, M.H.; Udoetok, I.A.; Wilson, L.D. Animal biopolymer-plant biomass composites: Synergism and improved sorption efficiency. J. Compos. Sci. 2020, 4, 15. [Google Scholar] [CrossRef] [Green Version]
- Sowmya, A.; Meenakshi, S. Effective removal of nitrate and phosphate anions from aqueous solutions using functionalised chitosan beads. Desalin. Water Treat. 2014, 52, 2583–2593. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, L.; Yang, B.; Huang, R. Removal of fluoride from aqueous solution using Zr(IV) immobilized cross-linked chitosan. Int. J. Biol. Macromol. 2015, 77, 15–23. [Google Scholar] [CrossRef]
- Jang, J.; Lee, D.S. Effective phosphorus removal using chitosan/Ca-organically modified montmorillonite beads in batch and fixed-bed column studies. J. Hazard. Mater. 2019, 375, 9–18. [Google Scholar] [CrossRef]
- Moret, A.; Rubio, J. Sulphate and molybdate ions uptake by chitin-based shrimp shells. Miner. Eng. 2003, 16, 715–722. [Google Scholar] [CrossRef]
- Haghsheno, R.; Mohebbi, A.; Hashemipour, H.; Sarrafi, A. Study of kinetic and fixed bed operation of removal of sulfate anions from an industrial wastewater by an anion exchange resin. J. Hazard. Mater. 2009, 166, 961–966. [Google Scholar] [CrossRef]
- Bureau of Indian Standards. IS: 3025 (Part 24): Method of Sampling and Test (Physical and Chemical) for Water and Wastewater, Part 24: Sulphates; Bureau of Indian Standards: New Delhi, India, 2009.
- Branca, C.; D’Angelo, G.; Crupi, C.; Khouzami, K.; Rifici, S.; Ruello, G.; Wanderlingh, U. Role of the OH and NH vibrational groups in polysaccharide-nanocomposite interactions: A FTIR-ATR study on chitosan and chitosan/clay films. Polymer 2016, 99, 614–622. [Google Scholar] [CrossRef]
- Udoetok, I.A.; Faye, O.; Wilson, L.D. Adsorption of phosphate dianions by hybrid inorganic-biopolymer polyelectrolyte complexes: Experimental and computational studies. ACS Appl. Polym. Mater. 2020, 2, 899–910. [Google Scholar] [CrossRef]
- Mahaninia, M.H.; Wilson, L.D. Modular cross-linked chitosan beads with calcium doping for enhanced adsorptive uptake of organophosphate anions. Ind. Eng. Chem. Res. 2016, 55, 11706–11715. [Google Scholar] [CrossRef]
- Tavares, L.; Esparza Flores, E.E.; Rodrigues, R.C.; Hertz, P.F.; Noreña, C.P.Z. Effect of deacetylation degree of chitosan on rheological properties and physical chemical characteristics of genipin-crosslinked chitosan beads. Food Hydrocoll. 2020, 106. [Google Scholar] [CrossRef]
- Talat, M.; Mohan, S.; Dixit, V.; Singh, D.K.; Hasan, S.H.; Srivastava, O.N. Effective removal of fluoride from water by coconut husk activated carbon in fixed bed column: Experimental and breakthrough curves analysis. Groundw. Sustain. Dev. 2018, 7, 48–55. [Google Scholar] [CrossRef]
- Chatterjee, S.; Mondal, S.; De, S. Design and scaling up of fixed bed adsorption columns for lead removal by treated laterite. J. Clean. Prod. 2018, 177, 760–774. [Google Scholar] [CrossRef]
- Basu, M.; Guha, A.K.; Ray, L. Adsorption of lead on lentil husk in fixed bed column bioreactor. Bioresour. Technol. 2019, 283, 86–95. [Google Scholar] [CrossRef]
- Banerjee, M.; Bar, N.; Basu, R.K.; Das, S.K. Comparative study of adsorptive removal of Cr(VI) ion from aqueous solution in fixed bed column by peanut shell and almond shell using empirical models and ANN. Environ. Sci. Pollut. Res. 2017, 24, 10604–10620. [Google Scholar] [CrossRef]
- Aichour, A.; Zaghouane-Boudiaf, H.; Zuki, F.B.M.; Aroua, M.K.; Ibbora, C.V. Low-Cost, biodegradable and highly effective adsorbents for batch and column fixed bed adsorption processes of methylene blue. J. Environ. Chem. Eng. 2019, 7, 103409. [Google Scholar] [CrossRef]
- Gouran-Orimi, R.; Mirzayi, B.; Nematollahzadeh, A.; Tardast, A. Competitive adsorption of nitrate in fixed-bed column packed with bio-inspired polydopamine coated zeolite. J. Environ. Chem. Eng. 2018, 6, 2232–2240. [Google Scholar] [CrossRef]
- Taty-Costodes, V.C.; Fauduet, H.; Porte, C.; Ho, Y.S. Removal of lead (II) ions from synthetic and real effluents using immobilized Pinus sylvestris sawdust: Adsorption on a fixed-bed column. J. Hazard. Mater. 2005, 123, 135–144. [Google Scholar] [CrossRef]
- Golie, W.M.; Upadhyayula, S. Continuous fixed-bed column study for the removal of nitrate from water using chitosan/alumina composite. J. Water Process Eng. 2016, 12, 58–65. [Google Scholar] [CrossRef]
- Dong, R.; Liu, Y.; Wang, X.; Huang, J. Adsorption of sulfate ions from aqueous solution by surfactant-modified palygorskite. J. Chem. Eng. Data 2011, 56, 3890–3896. [Google Scholar] [CrossRef]
- Chen, W.; Liu, H.C. Adsorption of sulfate in aqueous solutions by organo-nano-clay: Adsorption equilibrium and kinetic studies. J. Cent. South Univ. 2014, 21, 1974–1981. [Google Scholar] [CrossRef]
- Namasivayam, C.; Sangeetha, D. Application of coconut coir pith for the removal of sulfate and other anions from water. Desalination 2008, 219, 1–13. [Google Scholar] [CrossRef]
- Wu, C.H.; Kuo, C.Y.; Lin, C.F.; Lo, S.L. Modeling competitive adsorption of molybdate, sulfate, selenate, and selenite using a Freundlich-type multi-component isotherm. Chemosphere 2002, 47, 283–292. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, H.; Chen, K.; Zhou, J.; Liu, Q. Removal of heavy metal and sulfate ions by cellulose derivative-based biosorbents. Cellulose 2018, 25, 2531–2545. [Google Scholar] [CrossRef]
- Cao, W.; Dang, Z.; Zhou, X.Q.; Yi, X.Y.; Wu, P.X.; Zhu, N.W.; Lu, G.N. Removal of sulphate from aqueous solution using modified rice straw: Preparation, characterization and adsorption performance. Carbohydr. Polym. 2011, 85, 571–577. [Google Scholar] [CrossRef]
- Ntuli, F.; Falayi, T.; Thwanane, U. Removal of sulphates from acid mine drainage using desilicated fly ash slag. Waste Manag. Environ. VIII 2016, 1, 383–390. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.; Cannon, F.S.; Hou, P.; Byrne, T.; Nieto-Delgado, C. Sulfate removal from acid mine drainage using polypyrrole-grafted granular activated carbon. Carbon N. Y. 2014, 73, 51–60. [Google Scholar] [CrossRef]
- Runtti, H.; Tynjälä, P.; Tuomikoski, S.; Kangas, T.; Hu, T.; Rämö, J.; Lassi, U. Utilisation of barium-modified analcime in sulphate removal: Isotherms, kinetics and thermodynamics studies. J. Water Process Eng. 2017, 16, 319–328. [Google Scholar] [CrossRef] [Green Version]
- Sang, P.L.; Wang, Y.Y.; Zhang, L.Y.; Chai, L.Y.; Wang, H.Y. Effective adsorption of sulfate ions with poly(m-phenylenediamine) in aqueous solution and its adsorption mechanism. Trans. Nonferr. Met. Soc. China 2013, 23, 243–252. [Google Scholar] [CrossRef]







| Adsorbent | M (g) | pH | tb (min) | ts (min) | R (%) | qtotal (mg) | qmax (mg/g) | MTZ (mm) | Vb (mL) | Vs (mL) |
|---|---|---|---|---|---|---|---|---|---|---|
| Ca–CP | 11 | 4.5 | 75 | 300 | 57.00 | 513.0 | 46.6 | 150 | 225 | 900 |
| CP | 14 | 4.5 | 42 | 250 | 50.25 | 361.8 | 32.1 | 160.6 | 126 | 750 |
| CL–CP | 11 | 4.5 | 45 | 250 | 53.40 | 384.5 | 27.5 | 160.4 | 135 | 750 |
| CL–Ca–CP | 14 | 4.5 | 50 | 250 | 56.00 | 420.5 | 30.0 | 160 | 150 | 750 |
| Ca–CP | 11 | 6.5 | 45 | 180 | 50.50 | 318.6 | 29.0 | 150 | 135 | 540 |
| CP | 14 | 6.5 | 32 | 160 | 50.00 | 270.0 | 24.5 | 160 | 96 | 480 |
| CL–CP | 11 | 6.5 | 35 | 170 | 54.30 | 293.4 | 21.0 | 150.9 | 105 | 510 |
| CL–Ca–CP | 14 | 6.5 | 35 | 170 | 55.30 | 298.8 | 21.3 | 150.9 | 105 | 510 |
| Adsorbent | pH | Thomas Model Constant kth × 103 (L mg−1 h−1) | Adsorption Capacity qmax (mg/g) | R2 |
|---|---|---|---|---|
| Ca–CP | 6.5 | 2.3 | 30.3 | 0.98 |
| Ca–CP | 4.5 | 1.6 | 46.9 | 0.99 |
| CP | 6.5 | 2.3 | 27.2 | 0.98 |
| CP | 4.5 | 1.7 | 34.7 | 0.99 |
| CL–CP | 6.5 | 2.5 | 22.0 | 0.98 |
| CL–CP | 4.5 | 1.7 | 29.6 | 0.98 |
| Ca–CL–CP | 6.5 | 2.5 | 22.5 | 0.98 |
| Ca–CL–CP | 4.5 | 1.8 | 31.6 | 0.98 |
| Adsorbent | pH | Yoon-Nelson Constant kYN (h−1) | τ (h) | R2 |
|---|---|---|---|---|
| Ca–CP | 6.5 | 2.31 | 1.85 | 0.98 |
| Ca–CP | 4.5 | 1.60 | 2.95 | 0.99 |
| CP | 6.5 | 2.34 | 1.66 | 0.98 |
| CP | 4.5 | 2.12 | 1.77 | 0.98 |
| CL–CP | 6.5 | 2.85 | 1.75 | 0.98 |
| CL–CP | 4.5 | 2.29 | 1.78 | 0.98 |
| Ca–CL–CP | 6.5 | 2.55 | 1.71 | 0.98 |
| Ca–CL–CP | 4.5 | 1.84 | 2.46 | 0.98 |
| Flow Rate [Q] (mL/min) | Bed Height [Z] (mm) | Feed Concentration [Co] (mg/L) | Breakthrough Time [tb] (min) | Exhaustion Time [ts] (min) | Adsorption Capacity [qmax] (mg/g) | Removal [R] (%) |
|---|---|---|---|---|---|---|
| 3 | 200 | 1000 | 75 | 300 | 46.6 | 57.00 |
| 3 | 200 | 2000 | 22 | 182 | 49.1 | 85.71 |
| 3 | 300 | 1000 | 140 | 370 | 63.8 | 78 |
| 5 | 200 | 1000 | 45 | 210 | 50.5 | 52.85 |
| Flow Rate (mL/min) | Bed Height (mm) | Feed Concentration (mg/L) | kth × 103 (L mg−1 h−1) | Adsorption Capacity (mg/g) | Coefficient of Correlation (R2) |
|---|---|---|---|---|---|
| 3 | 200 | 1000 | 1.60 | 46.9 | 0.98 |
| 3 | 200 | 2000 | 0.86 | 56.7 | 0.92 |
| 3 | 300 | 1000 | 1.42 | 65.4 | 0.99 |
| 5 | 200 | 1000 | 1.97 | 52.7 | 0.97 |
| Cycle | Breakthrough Time (tb) | Exhaustion Time (ts) | Removal (%) | Adsorbed Sulfate qtotal (mg) | Adsorption Capacity (mg/g) |
|---|---|---|---|---|---|
| 1 | 75 | 300 | 57.0 | 513.0 | 46.6 |
| 2 | 75 | 300 | 56.5 | 509.0 | 46.3 |
| 3 | 45 | 250 | 56.2 | 425.0 | 36.6 |
| 4 | 20 | 150 | 55.0 | 268.2 | 24.4 |
| Adsorbent | Adsorption Capacity (mg/g) | Feed Concentration (mg/L) | Other Conditions | Ref. |
|---|---|---|---|---|
| Zirconium oxide-modified pomelo peel biochar | 35.2 | 300 | pH 5, 25 °C | [12] |
| Surfactant-modified palygorskite | 3.28 | 130 | pH 4, 35 °C | [35] |
| Organo-nano-clay modified with cetyltrimethylammonium bromide (CTAB) | 38 | 500 | pH 7, 40 °C | [36] |
| ZnCl2 activated coir pitch carbon | 49 | 40 | pH 4, 35 °C | [37] |
| γ-Al2O3 | 8.5 | ------ | pH 5.7 | [38] |
| CC/QAC | 526 | ------ | pH 5 | [39] |
| PG-Peat | 189.5 | 1835 | pH 2.4, 22 °C | [11] |
| Modified rice straw | 74.8 | 500 | pH 6.4, 25 °C | [40] |
| Desilicated fly ash | 147.1 | ------ | 35 °C | [41] |
| Polypyrolle-grafted granular activated carbon | 44.7 | 250 | pH 7, 20 °C | [42] |
| Ba-modified blast-furnace-slag-geopolymer | 119 | 865 | pH 7–8 | [43] |
| Poly(m-Phenylendiamine) | 109 | 109 | pH < 3 | [44] |
| Chitin | 156 | 2325 | pH 4.5 | [20] |
| Calcium-Chitosan pellet (Ca–CP) | 63.8 | 1000 | pH 4.5 | This study |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solgi, M.; G. Tabil, L.; D. Wilson, L. Modified Biopolymer Adsorbents for Column Treatment of Sulfate Species in Saline Aquifers. Materials 2020, 13, 2408. https://doi.org/10.3390/ma13102408
Solgi M, G. Tabil L, D. Wilson L. Modified Biopolymer Adsorbents for Column Treatment of Sulfate Species in Saline Aquifers. Materials. 2020; 13(10):2408. https://doi.org/10.3390/ma13102408
Chicago/Turabian StyleSolgi, Mostafa, Lope G. Tabil, and Lee D. Wilson. 2020. "Modified Biopolymer Adsorbents for Column Treatment of Sulfate Species in Saline Aquifers" Materials 13, no. 10: 2408. https://doi.org/10.3390/ma13102408
APA StyleSolgi, M., G. Tabil, L., & D. Wilson, L. (2020). Modified Biopolymer Adsorbents for Column Treatment of Sulfate Species in Saline Aquifers. Materials, 13(10), 2408. https://doi.org/10.3390/ma13102408