Multi-Scale Modeling of Microstructure Evolution during Multi-Pass Hot-Rolling and Cooling Process
Abstract
:1. Introduction
2. Experiments and FEM Simulation
3. Governing Equations and Numerical Methods of the CA Model
3.1. Model Description
3.2. Austenite Recrystallization
3.2.1. Dislocation Density Evolution
3.2.2. Nucleation of Austenite Recrystallization
3.2.3. Grain Growth and Coarsening
3.2.4. Uniform Topology Deformation
3.3. Austenite to Ferrite Transformation
3.3.1. Ferrite Nucleation
3.3.2. Ferrite Growth and Coarsening
3.3.3. Solute Drag Model
3.3.4. Carbon Diffusion
3.4. Coupling Scheme between CA and FEM Simulations
4. Results and Discussion
4.1. FEM Simulation of Hot-Rolling
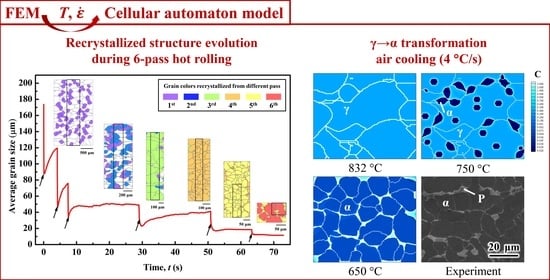
4.2. CA Simulation of the Hot-Rolling Process
4.3. CA Simulation of Cooling Process.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| γb | high-angle grain boundary energy: J m−2 |
| ε | strain |
| ɛc | critical strain for SRX nucleation |
| strain rate, s−1 | |
| θ0 | initial work hardening rate, MPa |
| κ | the grain boundary curvature, m−1 |
| Λ | half physical interface thickness, nm |
| μ | shear modulus of the γ-phase, Pa |
| ρ | dislocation density, m−2 |
| ρ0 | initial dislocation density, m−2 |
| ρc | critical dislocation density for DRX, m−2 |
| ρave | average dislocation density of the material, m−2 |
| average dislocation density of the deformed grain, m−2 | |
| average dislocation density of the recrystallized grain, m−2 | |
| σ | flow stress, Pa |
| σs | saturated stress, Pa |
| τ | dislocation line energy, J·m−1 |
| φ | α-phase volume fraction |
| χ | proportionality factor, J mol−1 mol.%−1 |
| α1,β, η, a, n’, A0, QA | constants for calculating dislocation density evolution |
| A | coefficient for calculating curvature |
| ASi | area of grain Si |
| b | the magnitude of the Burgers vector, m |
| C | DRX nucleation parameter |
| d | coefficient representing static recovery rate |
| d0, md QSRV | constants for calculating static recovery rate |
| average diameters for γ-, matrix, DRX, SRX, α-grains, μm | |
| carbon diffusion coefficients in the α- and γ-phases, m2 s−1 | |
| D0 | boundary self-diffusion coefficient, m2 s−1 |
| manganese diffusion coefficient across the α/γ interface, m2 s−1 | |
| Edef | deformation stored energy, J m−3 |
| Ec | critical deformation stored energy for SRX nucleation, J m−3 |
| average deformation stored energy of grain S, J m−3 | |
| E0 | binding energy of manganese, J mol−1 |
| ΔE | half potential difference of manganese between α- and γ-phases, J mol−1 |
| fRX, fα | volume fractions of recrystallized grains and α grains |
| ΔGV | driving force of the ferrite nucleation, J mol−1 |
| ΔGV,che | Gibbs chemical free energy difference between the α- and γ-phases, J mol−1 |
| ΔGche | chemical driving force of the γ→α transformation, J mol−1 |
| ΔGdis | solute drag pressure, J mol−1 |
| gnew | geometrical factor |
| HS,Max | maximum value of the stored energy in grain S, J m−3 |
| I | grain index |
| J | nucleation rate of ferrite, m−2 s−1 |
| k | Boltzmann constant, J K−1 |
| ke | equilibrium partitioning coefficient |
| k1,k2 | constants representing work hardening and dynamic recovery |
| K1K2 | constants for calculating the nucleation rate of ferrite |
| Kink | number of cells within the neighborhood belonging to grain S for a flat interface |
| l | dislocation mean free path, m |
| li | ratio of the final to initial length of vector along corresponding axis |
| L | distance of the cell (i, j) from the grain boundary, μm |
| f(L) | factor for deformation stored energy distribution |
| M | deformation matrix for topology mapping |
| Mb | high-angle grain boundary mobility, m4 J−1 s−1 |
| Mα/γ | interfacial mobility of the moving α/γ interface, mol m J−1 s−1 |
| pre-exponential factor, mol m J−1 s−1 | |
| nucleation rates for DRX and SRX, m−2 s−1 | |
| n | number of cells that belongs to grain S |
| N | number of the first and second nearest neighbors |
| NS | number of cells within the neighborhood belonging to grain S |
| Ng | number of grains in the calculation domain |
| P | driving pressure, J m−3 |
| Pα/γ | effective driving pressure for ferrite growth, J mol−1 |
| QN | activation energy for nucleation, KJ mol−1 |
| Qb | activation energy for grain-boundary motion, KJ mol−1 |
| Qα/γ | activation energy for atom motion at the interface, KJ mol−1 |
| R | universal gas constant, J mol−1 K−1 |
| SI, SII | states of the nearest and the second-nearest neighbor cells |
| T | absolute temperature, K |
| u,v | original and the new vectors of the CA cell space |
| V | velocity of grain boundary movement, m s−1 |
| Vα/γ | migration velocity of the α/γ interface, m s−1 |
| Vm | molar volume of austenite, m3 mol−1 |
| equilibrium carbon concentration of the α-phase, mol.% | |
| equilibrium carbon concentration of the γ-phase, mol.% | |
| actual carbon concentration of the γ-phase at the α/γ interface, mol.% | |
| manganese concentration in the bulk matrix, mol.% | |
| y | distance from the interface, μm |
| xMn(y) | the manganese concentration profile |
| E(y) | the interaction potential of manganese |
| Z | nucleation parameter for SRX, J−1 s−1 |
References
- Huang, K.; Logé, R.E. A Review of Dynamic Recrystallization Phenomena in Metallic Materials. Mater. Des. 2016, 111, 548–574. [Google Scholar] [CrossRef]
- Zhao, L.; Park, N.; Tian, Y.; Shibata, A.; Tsuji, N. Mechanism of Dynamic Formation of Ultrafine Ferrite Grains during High Temperature Processing in Steel. Adv. Eng. Mater. 2017, 19, 1600778. [Google Scholar] [CrossRef]
- Fang, Y.; Chen, X.; Madigan, B.; Cao, H.; Konovalov, S. Effects of Strain Rate on the Hot Deformation Behavior and Dynamic Recrystallization in China Low Activation Martensitic Steel. Fusion Eng. Des. 2016, 103, 21–30. [Google Scholar] [CrossRef]
- Nicolaÿ, A.; Fiorucci, G.; Franchet, J.M.; Cormier, J.; Bozzolo, N. Influence of Strain Rate on Subsolvus Dynamic and Post-Dynamic Recrystallization Kinetics of Inconel 718. Acta Mater. 2019, 174, 406–417. [Google Scholar] [CrossRef]
- Yu, S.; Du, L.X.; Hu, J.; Misra, R.D.K. Effect of Hot Rolling Temperature on the Microstructure and Mechanical Properties of Ultra-Low Carbon Medium Manganese Steel. Mater. Sci. Eng. A 2018, 731, 149–155. [Google Scholar] [CrossRef]
- Ghosh, S.; Komi, J.; Mula, S. Flow Stress Characteristics and Design of Innovative 3-Steps Multiphase Control Thermomechanical Processing to Produce Ultrafine Grained Bulk Steels. Mater. Des. 2020, 186, 108297. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, J.; Han, Y.; Liu, R.; Zou, D.; Qiao, G. Metadynamic Recrystallization Behavior of As-Cast 904L Superaustenitic Stainless Steel. J. Iron Steel Res. Int. 2016, 23, 151–159. [Google Scholar] [CrossRef]
- Raabe, D. Cellular Automata in Materials Science with Particular Reference to Recrystallization Simulation. Annu. Rev. Mater. Res. 2002, 32, 53–76. [Google Scholar] [CrossRef]
- Chen, F.; Zhu, H.; Zhang, H.; Cui, Z. Mesoscale Modeling of Dynamic Recrystallization: Multilevel Cellular Automaton Simulation Framework. Metall. Mater. Trans. A 2020, 51, 1286–1303. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, D.; Yang, Y.; Wang, J.; Liu, C.; Zhang, Z.; Wang, H. Modeling and Simulation of Dynamic Recrystallization for Inconel 718 in the Presence of Delta Phase Particles Using a Developed Cellular Automaton Model. Model. Simul. Mater. Sci. Eng. 2019, 27, 035002. [Google Scholar] [CrossRef]
- Bararpour, S.M.; Jamshidi Aval, H.; Jamaati, R. Cellular Automaton Modeling of Dynamic Recrystallization in Al-Mg Alloy Coating Fabricated Using the Friction Surfacing Process. Surf. Coat. Technol. 2021, 407, 126784. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Xu, B.; Xu, X.; Zhao, W. Prediction of Microstructure Gradient Distribution in Machined Surface Induced by High Speed Machining through a Coupled FE and CA Approach. Mater. Des. 2020, 196, 109133. [Google Scholar] [CrossRef]
- Madej, Ł.; Sitko, M.; Legwand, A.; Perzynski, K.; Michalik, K. Development and Evaluation of Data Transfer Protocols in the Fully Coupled Random Cellular Automata Finite Element Model of Dynamic Recrystallization. J. Comput. Sci. 2018, 26, 66–77. [Google Scholar] [CrossRef]
- Kim, D.-K.; Woo, W.; Park, W.-W.; Im, Y.-T.; Rollett, A. Mesoscopic Coupled Modeling of Texture Formation during Recrystallization Considering Stored Energy Decomposition. Comput. Mater. Sci. 2017, 129, 55–65. [Google Scholar] [CrossRef] [Green Version]
- Shen, G.; Hu, B.; Zheng, C.; Gu, J.; Li, D. Coupled Simulation of Ferrite Recrystallization in a Dual-Phase Steel Considering Deformation Heterogeneity at Mesoscale. Comput. Mater. Sci. 2018, 149, 191–201. [Google Scholar] [CrossRef]
- Li, H.; Sun, X.; Yang, H. A Three-Dimensional Cellular Automata-Crystal Plasticity Finite Element Model for Predicting the Multiscale Interaction among Heterogeneous Deformation, DRX Microstructural Evolution and Mechanical Responses in Titanium Alloys. Int. J. Plast. 2016, 87, 154–180. [Google Scholar] [CrossRef]
- Barkóczy, P.; Roósz, A.; Geiger, J. Simulation of Recrystallization by Cellular Automaton Method. Mater. Sci. Forum 2003, 414–415, 359–364. [Google Scholar] [CrossRef]
- Zheng, C.; Xiao, N.; Li, D.; Li, Y. Microstructure Prediction of the Austenite Recrystallization during Multi-Pass Steel Strip Hot Rolling: A Cellular Automaton Modeling. Comput. Mater. Sci. 2008, 44, 507–514. [Google Scholar] [CrossRef]
- Chen, F.; Cui, Z. Mesoscale Simulation of Microstructure Evolution during Multi-Stage Hot Forging Processes. Model. Simul. Mater. Sci. Eng. 2012, 20, 045008. [Google Scholar] [CrossRef]
- Łach, Ł.; Svyetlichnyy, D. Multiscale Model of Shape Rolling Taking into Account the Microstructure Evolution—Frontal Cellular Automata. Adv. Mater. Res. 2014, 998–999, 545–548. [Google Scholar] [CrossRef]
- Łach, Ł.; Svyetlichnyy, D. Frontal Cellular Automata Simulations of Microstructure Evolution during Shape Rolling. Mater. Res. Innov. 2014, 18, S6-295. [Google Scholar] [CrossRef]
- Svyetlichnyy, D. Simulation of Microstructure Evolution during Shape Rolling with the Use of Frontal Cellular Automata. ISIJ Int. 2012, 52, 559–568. [Google Scholar] [CrossRef] [Green Version]
- Zheng, C.; Xiao, N.; Hao, L.; Li, D.; Li, Y. Numerical Simulation of Dynamic Strain-Induced Austenite-Ferrite Transformation in a Low Carbon Steel. Acta Mater. 2009, 57, 2956–2968. [Google Scholar] [CrossRef]
- Zheng, C.; Raabe, D. Interaction between Recrystallization and Phase Transformation during Intercritical Annealing in a Cold-Rolled Dual-Phase Steel: A Cellular Automaton Model. Acta Mater. 2013, 61, 5504–5517. [Google Scholar] [CrossRef]
- Lan, Y.J.; Xiao, N.M.; Li, D.Z.; Li, Y.Y. Mesoscale Simulation of Deformed Austenite Decomposition into Ferrite by Coupling a Cellular Automaton Method with a Crystal Plasticity Finite Element Model. Acta Mater. 2005, 53, 991–1003. [Google Scholar] [CrossRef]
- Su, B.; Ma, Q.; Han, Z. Modeling of Austenite Decomposition during Continuous Cooling Process in Heat Treatment of Hypoeutectoid Steel with Cellular Automaton Method. Steel Res. Int. 2017, 88, 1600490. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, Y.; Wang, C.; Liu, P.X.; Liang, W.K.; Li, J. Modeling of the Austenitization of Ultra-High Strength Steel with Cellular Automation Method. Metall. Mater. Trans. A 2014, 45, 3161–3171. [Google Scholar] [CrossRef]
- Su, B.; Han, Z.; Liu, B. Cellular Automaton Modeling of Austenite Nucleation and Growth in Hypoeutectoid Steel during Heating Process. ISIJ Int. 2013, 53, 527–534. [Google Scholar] [CrossRef] [Green Version]
- An, D.; Baik, S.; Pan, S.; Zhu, M.; Isheim, D.; Krakauer, B.W.; Seidman, D.N. Evolution of Microstructure and Carbon Distribution During Heat Treatments of a Dual-Phase Steel: Modeling and Atom-Probe Tomography Experiments. Metall. Mater. Trans. A 2018, 50, 436–450. [Google Scholar] [CrossRef]
- An, D.; Chen, S.; Sun, D.; Pan, S.; Krakauer, B.W.; Zhu, M. A Cellular Automaton Model Integrated with CALPHAD-Based Thermodynamic Calculations for Ferrite-Austenite Phase Transformations in Multicomponent Alloys. Comput. Mater. Sci. 2019, 166, 210–220. [Google Scholar] [CrossRef]
- Bos, C.; Mecozzi, M.G.; Sietsma, J. A Microstructure Model for Recrystallisation and Phase Transformation during the Dual-Phase Steel Annealing Cycle. Comput. Mater. Sci. 2010, 48, 692–699. [Google Scholar] [CrossRef]
- Vertyagina, Y.; Mahfouf, M.; Xu, X. 3D Modelling of Ferrite and Austenite Grain Coarsening Using Real-Valued Cellular Automata Based on Transition Function. J. Mater. Sci. 2013, 48, 5517–5527. [Google Scholar] [CrossRef]
- Li, D.Z.; Xiao, N.M.; Lan, Y.J.; Zheng, C.W.; Li, Y.Y. Growth Modes of Individual Ferrite Grains in the Austenite to Ferrite Transformation of Low Carbon Steels. Acta Mater. 2007, 55, 6234–6249. [Google Scholar] [CrossRef]
- Chen, H.; van der Zwaag, S. A General Mixed-Mode Model for the Austenite-to-Ferrite Transformation Kinetics in Fe–C–M Alloys. Acta Mater. 2014, 72, 1–12. [Google Scholar] [CrossRef]
- Purdy, G.R.; Brechet, Y.J.M. A Solute Drag Treatment of the Effects of Alloying Elements on the Rate of the Proeutectoid Ferrite Transformation in Steels. Acta Metall. Mater. 1995, 43, 3763–3774. [Google Scholar] [CrossRef]
- Chen, F.; Cui, Z.; Liu, J.; Chen, W.; Chen, S. Mesoscale Simulation of the High-Temperature Austenitizing and Dynamic Recrystallization by Coupling a Cellular Automaton with a Topology Deformation Technique. Mater. Sci. Eng. A 2010, 527, 5539–5549. [Google Scholar] [CrossRef]
- Humphreys, J.; Rohrer, G.S.; Rollett, A. Chapter 7—Recrystallization of Single-Phase Alloys. In Recrystallization and Related Annealing Phenomena, 3rd ed.; Humphreys, J., Rohrer, G.S., Rollett, A., Eds.; Elsevier: Oxford, UK, 2017; pp. 245–304. ISBN 978-0-08-098235-9. [Google Scholar]
- Mecking, H.; Kocks, U.F. Kinetics of Flow and Strain-Hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Hatta, N.; Kokado, J.; Kikuchi, S.; Takuda, H. Modelling on Flow Stress of Plain Carbon Steel at Elevated Temperatures. Steel Res. 1985, 56, 575–582. [Google Scholar] [CrossRef]
- Yoshie, A.; Fujita, T.; Fujioka, M.; Okamoto, K.; Morikawa, H. Formulation of the Decrease in Dislocation Density of Deformed Austenite Due to Static Recovery and Recrystallization. ISIJ Int. 1996, 36, 474–480. [Google Scholar] [CrossRef]
- Barnoush, A.; Asgari, M.; Johnsen, R. Resolving the Hydrogen Effect on Dislocation Nucleation and Mobility by Electrochemical Nanoindentation. Scr. Mater. 2012, 66, 414–417. [Google Scholar] [CrossRef]
- Ivasishin, O.M.; Shevchenko, S.V.; Vasiliev, N.L.; Semiatin, S.L. A 3-D Monte-Carlo (Potts) Model for Recrystallization and Grain Growth in Polycrystalline Materials. Mater. Sci. Eng. A 2006, 433, 216–232. [Google Scholar] [CrossRef]
- Ding, R.; Guo, Z.X. Coupled Quantitative Simulation of Microstructural Evolution and Plastic Flow during Dynamic Recrystallization. Acta Mater. 2001, 49, 3163–3175. [Google Scholar] [CrossRef]
- Chen, F.; Qi, K.; Cui, Z.; Lai, X. Modeling the Dynamic Recrystallization in Austenitic Stainless Steel Using Cellular Automaton Method. Comput. Mater. Sci. 2014, 83, 331–340. [Google Scholar] [CrossRef]
- Fan, X.G.; Yang, H.; Sun, Z.C.; Zhang, D.W. Quantitative Analysis of Dynamic Recrystallization Behavior Using a Grain Boundary Evolution Based Kinetic Model. Mater. Sci. Eng. A 2010, 527, 5368–5377. [Google Scholar] [CrossRef]
- Roberts, W.; Ahlblom, B. A Nucleation Criterion for Dynamic Recrystallization during Hot Working. Acta Metall. 1978, 26, 801–813. [Google Scholar] [CrossRef]
- Takeuchi, S.; Argon, A.S. Steady-State Creep of Single-Phase Crystalline Matter at High Temperature. J. Mater. Sci. 1976, 11, 1542–1566. [Google Scholar] [CrossRef]
- Davies, C.H.J. Growth of Nuclei in a Cellular Automaton Simulation of Recrystallisation. Scr. Mater. 1997, 36, 35–40. [Google Scholar] [CrossRef]
- Kugler, G.; Turk, R. Modeling the Dynamic Recrystallization under Multi-Stage Hot Deformation. Acta Mater. 2004, 52, 4659–4668. [Google Scholar] [CrossRef]
- Song, X.; Rettenmayr, M. Modelling Study on Recrystallization, Recovery and Their Temperature Dependence in Inhomogeneously Deformed Materials. Mater. Sci. Eng. A 2002, 332, 153–160. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, C.-W.; Li, D.-Z. A Multi-Phase Field Model for Static Recrystallization of Hot Deformed Austenite in a C-Mn Steel. Acta Metall. Sin. Engl. Lett. 2018, 31, 208–215. [Google Scholar] [CrossRef]
- Kremeyer, K. Cellular Automata Investigations of Binary Solidification. J. Comput. Phys. 1998, 142, 243–263. [Google Scholar] [CrossRef]
- Umemoto, M.; Guo, Z.H.; Tamra, I. Effect of Cooling Rate on Grain Size of Ferrite in Carbon Steel. Mater. Sci. Technol. 1987, 3, 249–255. [Google Scholar] [CrossRef]
- Offerman, S.E.; van Dijk, N.H.; Sietsma, J.; Grigull, S.; Lauridsen, E.M.; Margulies, L.; Poulsen, H.F.; Rekveldt, M.T.; van der Zwaag, S. Grain Nucleation and Growth During Phase Transformations. Science 2002, 298, 1003–1005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krielaart, G.P.; Van Der Zwaag, S. Kinetics of γ → α Phase Transformation in Fe-Mn Alloys Containing Low Manganese. Mater. Sci. Technol. 1998, 14, 10–18. [Google Scholar] [CrossRef]
- Fazeli, F.; Militzer, M. Application of Solute Drag Theory to Model Ferrite Formation in Multiphase Steels. Metall. Mater. Trans. A 2005, 36, 1395–1405. [Google Scholar] [CrossRef]
- Zhu, B.; Militzer, M. Phase-Field Modeling for Intercritical Annealing of a Dual-Phase Steel. Metall. Mater. Trans. A 2015, 46, 1073–1084. [Google Scholar] [CrossRef]
- Militzer, M.; Mecozzi, M.; Sietsma, J.; Van Der Zwaag, S. Three-Dimensional Phase Field Modelling of the Austenite-to-Ferrite Transformation. Acta Mater. 2006, 54, 3961–3972. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y.; Wu, D.; Zhao, X.; Wang, G. Investigation on recrystallization and dislocation densityin high temperature deformed of C-Mn steel. Res. Iron Steel 2004, 32, 35–38. [Google Scholar] [CrossRef]
- Sun, W.P.; Hawbolt, E.B. Comparison between Static and Metadynamic Recrystallization—An Application to the Hot Rolling of Steels. ISIJ Int. 1997, 37, 1000–1009. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, S.; Wang, B.; Shi, Z.; Zhang, R.; Fu, W. Effect of Grain Size on Dynamic Recrystallization and Hot-Ductility Behaviors in High-Nitrogen CrMn Austenitic Stainless Steel. Metall. Mater. Trans. A 2014, 45, 3631–3639. [Google Scholar] [CrossRef]
- Dehghan-Manshadi, A.; Hodgson, P.D. Dependency of Recrystallization Mechanism to the Initial Grain Size. Metall. Mater. Trans. A 2008, 39, 2830. [Google Scholar] [CrossRef] [Green Version]








| Pass 1 | Pass 2 | Pass 3 | Pass 4 | Pass 5 | Pass 6 | |
|---|---|---|---|---|---|---|
| Strain, ε | 0.288 | 0.405 | 0.288 | 0.511 | 0.693 | 0.889 |
| Initial rolling Temperature (°C) | 1027 ± 10 | 1023 ± 10 | 1023 ± 10 | 1000 ± 10 | 950 ± 10 | 910 ± 10 |
| Pass 1 | Pass 2 | Pass 3 | Pass 4 | Pass 5 | Pass 6 | Cooling | |
|---|---|---|---|---|---|---|---|
| Initial simulation domain size (CA cells) | 250 × 750 | 111 × 563 | 110 × 752 | 73 × 565 | 80 × 680 | 100 × 400 | 240 × 200 |
| CA space step, Δx (μm) | 4.8 | 4.8 | 2.4 | 2.4 | 1.2 | 0.6 | 0.3 |
| Pass 1 | Pass 2 | Pass 3 | Pass 4 | Pass 5 | Pass 6 | |
|---|---|---|---|---|---|---|
| Strain rate, (s−1) | 3.724 | 4.770 | 3.964 | 5.632 | 10.000 | 12.024 |
| Pass Number | Initial | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Average grain size, (μm) | 174 | 120 | 76 | 49 | 41 | 19 | 12 |
| Average matrix grain size, (μm) | 174 | 147 | 87 | 27 | 20 | 12 | 8 |
| Average DRX grain size, (μm) | -- | 93 | 63 | 72 | 33 | 15 | -- |
| Average SRX grain size, (μm) | -- | -- | -- | -- | 45 | 23 | 19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Zou, X.; An, D.; Krakauer, B.W.; Zhu, M. Multi-Scale Modeling of Microstructure Evolution during Multi-Pass Hot-Rolling and Cooling Process. Materials 2021, 14, 2947. https://doi.org/10.3390/ma14112947
Lin X, Zou X, An D, Krakauer BW, Zhu M. Multi-Scale Modeling of Microstructure Evolution during Multi-Pass Hot-Rolling and Cooling Process. Materials. 2021; 14(11):2947. https://doi.org/10.3390/ma14112947
Chicago/Turabian StyleLin, Xian, Xinyi Zou, Dong An, Bruce W. Krakauer, and Mingfang Zhu. 2021. "Multi-Scale Modeling of Microstructure Evolution during Multi-Pass Hot-Rolling and Cooling Process" Materials 14, no. 11: 2947. https://doi.org/10.3390/ma14112947
APA StyleLin, X., Zou, X., An, D., Krakauer, B. W., & Zhu, M. (2021). Multi-Scale Modeling of Microstructure Evolution during Multi-Pass Hot-Rolling and Cooling Process. Materials, 14(11), 2947. https://doi.org/10.3390/ma14112947