Effect of Tool Geometry Parameters on the Formability of a Camera Cover in the Deep Drawing Process
Abstract
:1. Introduction
2. Numerical Simulation and Experiment
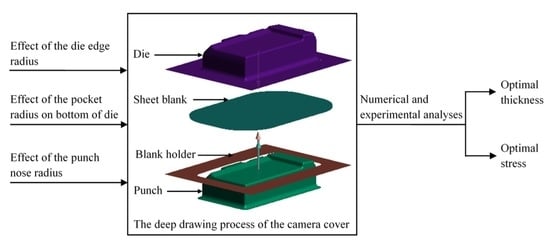
2.1. Camera Cover Model
2.2. Material Definition
2.3. Numerical and Experimental Conditions
3. Results and Discussion
3.1. Thickness and Stress Distributions
3.2. The Effect of Single Parameter on Thickness and Stress
3.2.1. The Die Edge Radius
3.2.2. The Pocket Radius on the Bottom of Die
3.2.3. The Punch Nose Radius
3.3. Optimization of the Thickness and Stress of the Camera Cover
3.4. The Comparison of Numerical and Experimental Results
4. Conclusions
- The thickness distribution relating to the stress distribution of the drawn part could be found by numerical and experimental analyses. The results clearly described that the changes on the thickness and on the stress were the consequence of varying tool geometry parameters. It was observed that lower thinning was obtained at the corners due to higher values of the die edge radius, punch nose radius and pocket radius of die. The thickness was the smallest and the stress was the highest at one of the bottom corners where the biaxial stretching was predominant mode of deformation.
- The objective functions describing the effects of tool geometry parameters on the optimal thickness and stress of the drawn part were established by the statistic method. The optimization of tool geometry parameters including the die edge radius, the pocket radius on the bottom of die and punch nose radius had improved the formability of the camera cover with more uniform thickness distribution. In this study, a general rule to optimize the thickness distribution was to design the die and punch with the best values of the die edge radius of 10 times, the pocket radius on the bottom of die of 5 times and the punch nose radius of 2.5 times the sheet thickness.
- The thickening, wrinkling and splitting defects could also be prevented when the tool geometry parameters were optimized. It demonstrated that the quality of the camera cover was improved with a maximum thinning of 25 %, and it was within the suggested maximum allowable thickness reduction of 45% for various industrial applications.
- The regression equations obtained from this study can be referred for a wide range of products, especially for rectangular shaped products with many bottom corners, for improving the formability by the suitable selection of tool geometry parameters. However, the equation coefficients may different, depending on the materials, shape and dimension of the specific products.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| 3D-part | Three-dimensional part |
| LDR | Limiting drawing rate |
| CMM | Coordinate measuring machine |
| RD | Die edge radius |
| RD1 | Pocket radius on the bottom of die |
| RP | Punch nose radius |
| σ | Von-Mises stress |
| t | Thickness |
| v | Press speed |
| µ | Friction coefficient |
| q | Holder pressure |
References
- Goodarzi, M.; Kuboki, T.; Murata, M. Effect of die corner radius on the formability and dimensional accuracy of tube shear bending. Int. J. Adv. Manuf. Technol. 2007, 35, 66–74. [Google Scholar] [CrossRef]
- Ayari, F.; Bayraktar, E. Parametric finite element analysis for a square cup deep drawing process. J. Achiev. Mater. Manuf. 2011, 48, 64–86. [Google Scholar]
- Najmeddin, A.; Abotaleb, J. Theoretical and experimental analysis of deep drawing cylindrical cup. J. Miner. Mater. Charact. Eng. 2013, 1, 336–342. [Google Scholar]
- Saani, S.; Mostafa, H.; Abdessalem, C. Single stage steel cup deep drawing analysis using finite element simulation. Int. J. Eng. Res. 2015, 4, 395–400. [Google Scholar]
- Reddy, A.C.S.; Rajesham, S.; Reddy, P.R.; Kumar, T.P.; Goverdhan, J. An experimental study on effect of process parameters in deep drawing using Taguchi technique. Int. J. Eng. Sci. Technol. 2015, 7, 21–32. [Google Scholar] [CrossRef] [Green Version]
- Djavanroodi, F.; Derogar, A. Experimental and numerical evaluation of forming limit diagram for Ti6Al4V titanium and Al6061-T6 aluminum alloys sheets. Mater. Des. 2010, 31, 4866–4875. [Google Scholar] [CrossRef]
- Younis, K.M.; Jaber, A.S. Experimental and theoretical study of square deep drawing. J. Eng. Technol. 2011, 29, 2456–2467. [Google Scholar]
- Hamed, K. Studying the effect of sharpen matrix radius on deep drawing operation. JLS 2014, 4, 2879–2884. [Google Scholar]
- Zein, H.; El-Sherbiny, M.; Abd-Rabou, M.; El-Shazly, M. Effect of die design parameters on thinning of sheet metal in the deep drawing process. Am. J. Mech. Eng. 2013, 1, 20–29. [Google Scholar] [CrossRef] [Green Version]
- Colgan, M.; Monaghan, J. Deep Drawing Process: Analysis and Experiment. J. Mater. Process. Technol. 2003, 132, 35–41. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Kim, Y.S.; Jung, D.W. Coupled thermomechanical finite element analysis to improve press formability for camera shape using AZ31B magnesium alloy sheet. Met. Mater. Int. 2012, 18, 583–595. [Google Scholar]
- Ulibarri, U.; Galdos, L.; De Argandoña, E.S.; Mendiguren, J. Experimental and numerical simulation investigation on deep drawing process of inconel 718 with and without intermediate annealing thermal treatments. Appl. Sci. 2020, 10, 581. [Google Scholar] [CrossRef] [Green Version]
- Paul, W.; Muhammad, J.Q.; Andrzej, R. Effect of friction and back pressure on the formability of superplastically formed aluminium alloy sheet. Key Eng. Mater. 2011, 473, 532–539. [Google Scholar]
- Gavas, M. Increasing the deep drawability of Al-1050 Aluminum sheet using multi-point blank holder. METABK 2006, 45, 109–113. [Google Scholar]
- Karali, M. Examination of the strength and ductility of AA-1050 material shaped with the multi-stage deep drawing method. Arch. Metall. Mater. 2011, 56, 223–230. [Google Scholar] [CrossRef] [Green Version]
- Modi, B.; Kumar, D.R. Optimization of process parameters to enhance formability of AA 5182 alloy in deep drawing of square cups by hydroforming. J. Mech. Sci. Technol. 2019, 33, 5337–5346. [Google Scholar] [CrossRef]
- Boissiere, R.; Vacher, P.; Blandin, J.J. Influence of the punch geometry and sample size on the deep-drawing limits in expansion of an aluminium alloy. Int. J. Mater. Form. 2010, 3, 135–138. [Google Scholar] [CrossRef]
- Lin, B.T.; Yang, C.Y. Applying the Taguchi method to determine the influences of a microridge punch design on the deep drawing. Int. J. Adv. Manuf. Technol. 2017, 88, 2109–2119. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Park, J.G.; Kim, Y.S. Ductile Fracture Prediction in Rotational Incremental Forming for Magnesium Alloy Sheets Using Combined Kinematic/Isotropic Hardening Model. Metall. Mater. Trans. A 2010, 41A, 1983–1994. [Google Scholar] [CrossRef]
- Venkateswarlu, G.; Davidson, M.J.; Tagore, G.R.N. Influence of process parameters on the cup drawing of aluminium 7075 sheet. Int. J. Eng. Sci. Technol. 2010, 2, 41–49. [Google Scholar] [CrossRef]
- Li, Y.; Luo, M.; Gerlach, J.; Wierzbicki, T. Prediction of shear-induced fracture in sheet metal forming. J. Mater. Process. Technol. 2010, 210, 1858–1869. [Google Scholar] [CrossRef]
- Ivana, S. Handbook of Die Design, 2nd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Pourkamali, A.; Shahabizadeh, M.; Babaee, B. Finite element simulation of multi stage deep drawing processes & comparison with experimental results. World Acad. Sci. Eng. Technol. 2012, 6, 553–557. [Google Scholar]
- Rydz, D.; Stradomski, G.; Szarek, A.; Kubik, K.; Kordas, P. The analysis of pressed cups producing possibilities from rolled bimetallic Al-1050 + Cu-M1E sheets. Materials 2020, 13, 2413. [Google Scholar] [CrossRef] [PubMed]
- Sherbiny, M.E.; Zein, H.; Abd-Rabou, M.; Shazly, M.E. Thinning and residual stresses of sheet metal in the deep drawing process. Mater. Des. 2014, 55, 869–879. [Google Scholar] [CrossRef]
- Prasad, K.S.; Panda, S.K.; Kar, S.K.; Murty, S.V.S.N.; Sharma, S.C. Prediction of fracture and deep drawing behavior of solution treated Inconel-718 sheets: Numerical modeling and experimental validation. Mater. Sci. Eng. A 2018, 733, 393–407. [Google Scholar] [CrossRef]

























| Elastic Modulus (GPa) | Yield Strength (MPa) | Tensile Strength (MPa) | Density (kg/m3) | Poisson’s Ratio | Hardness (HB) |
|---|---|---|---|---|---|
| 71 | 95 | 150 | 2.71 | 0.3 | 34 |
| RD (mm) | RD1 (mm) | Rp (mm) |
|---|---|---|
| 3.0–8.0 | 2.0–4.0 | 0.8–2.0 |
| RD (mm) | t (mm) | σ (MPa) |
|---|---|---|
| 3.0 | 0.490 | 156.0 |
| 4.0 | 0.500 | 148.2 |
| 5.0 | 0.508 | 145.0 |
| 6.0 | 0.513 | 142.5 |
| 7.0 | 0.515 | 141.0 |
| 8.0 | 0.516 | 140.0 |
| RD1 (mm) | t (mm) | σ (MPa) |
|---|---|---|
| 2.0 | 0.516 | 143.0 |
| 2.5 | 0.520 | 141.0 |
| 3.0 | 0.522 | 140.0 |
| 3.5 | 0.525 | 139.0 |
| 4.0 | 0.526 | 138.5 |
| RP (mm) | t (mm) | σ (MPa) |
|---|---|---|
| 0.8 | 0.499 | 147.0 |
| 1.0 | 0.509 | 145.0 |
| 1.2 | 0.511 | 144.0 |
| 1.4 | 0.523 | 140.0 |
| 1.6 | 0.533 | 137.0 |
| 1.8 | 0.545 | 134.0 |
| 2.0 | 0.566 | 133.0 |
| Input Parameters | Max | Mean | Min | Coding Variables | Max | Mean | Min |
|---|---|---|---|---|---|---|---|
| RD | 8.0 | 5.5 | 3.0 | X1 | 1 | 0 | −1 |
| RD1 | 4.0 | 3.0 | 2.0 | X2 | 1 | 0 | −1 |
| RP | 2.0 | 1.4 | 0.8 | X3 | 1 | 0 | −1 |
| No. | X0 | X1 | X2 | X3 | X1 X2 | X1 X3 | X2 X3 | X1 X2 X3 | X1′ | X2′ | X3′ | t (mm) | σ (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | + | − | − | − | + | + | + | − | 0.27 | 0.27 | 0.27 | 0.451 | 163 |
| 2 | + | + | − | − | − | − | + | + | 0.27 | 0.27 | 0.27 | 0.498 | 144 |
| 3 | + | − | + | − | − | + | − | + | 0.27 | 0.27 | 0.27 | 0.463 | 160 |
| 4 | + | + | + | − | + | − | − | 0.27 | 0.27 | 0.27 | 0.506 | 143 | |
| 5 | + | − | − | + | + | − | − | + | 0.27 | 0.27 | 0.27 | 0.472 | 157 |
| 6 | + | + | − | + | − | + | − | − | 0.27 | 0.27 | 0.27 | 0.559 | 130 |
| 7 | + | − | + | + | − | − | + | − | 0.27 | 0.27 | 0.27 | 0.479 | 154 |
| 8 | + | + | + | + | + | + | + | + | 0.27 | 0.27 | 0.27 | 0.572 | 126 |
| 9 | + | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −0.73 | −0.73 | −0.73 | 0.524 | 139 |
| 10 | + | 1.215 | 0 | 0 | 0 | 0 | 0 | 0 | 0.746 | −0.73 | −0.73 | 0.539 | 133 |
| 11 | + | −1.215 | 0 | 0 | 0 | 0 | 0 | 0 | 0.746 | −0.73 | −0.73 | 0.427 | 167 |
| 12 | + | 0 | 1.215 | 0 | 0 | 0 | 0 | 0 | −0.73 | 0.746 | −0.73 | 0.529 | 139 |
| 13 | + | 0 | −1.215 | 0 | 0 | 0 | 0 | 0 | −0.73 | 0.746 | −0.73 | 0.521 | 141 |
| 14 | + | 0 | 0 | 1.215 | 0 | 0 | 0 | 0 | −0.73 | −0.73 | 0.746 | 0.557 | 134 |
| 15 | + | 0 | 0 | −1.215 | 0 | 0 | 0 | 0 | −0.73 | −0.73 | 0.746 | 0.494 | 148 |
| RD (mm) | RD1 (mm) | RP (mm) | Simulation t (mm) | Experiment t (mm) | |
|---|---|---|---|---|---|
| Case I (Random) | 5.0 | 2.0 | 0.8 | 0.46 | 0.48 |
| Case II (Optimum) | 8.0 | 4.0 | 2.0 | 0.58 | 0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Do, T.T.; Minh, P.S.; Le, N. Effect of Tool Geometry Parameters on the Formability of a Camera Cover in the Deep Drawing Process. Materials 2021, 14, 3993. https://doi.org/10.3390/ma14143993
Do TT, Minh PS, Le N. Effect of Tool Geometry Parameters on the Formability of a Camera Cover in the Deep Drawing Process. Materials. 2021; 14(14):3993. https://doi.org/10.3390/ma14143993
Chicago/Turabian StyleDo, Thanh Trung, Pham Son Minh, and Nhan Le. 2021. "Effect of Tool Geometry Parameters on the Formability of a Camera Cover in the Deep Drawing Process" Materials 14, no. 14: 3993. https://doi.org/10.3390/ma14143993
APA StyleDo, T. T., Minh, P. S., & Le, N. (2021). Effect of Tool Geometry Parameters on the Formability of a Camera Cover in the Deep Drawing Process. Materials, 14(14), 3993. https://doi.org/10.3390/ma14143993