Study of High-Temperature Behaviour of ZnO by Ab Initio Molecular Dynamics Simulations and X-ray Absorption Spectroscopy
Abstract
:1. Introduction
2. Experimental Details
3. Computational Details
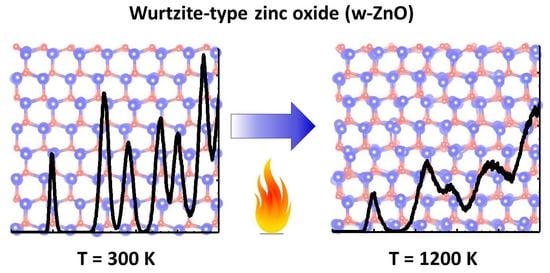
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AIMD | Ab Initio Molecular Dynamics |
| BADF | Bond Angle Distribution Functions |
| DFT | Density Functional Theory |
| EXAFS | Extended X-ray Absorption Fine Structure |
| FT | Fourier Transform |
| MS | Multiple-Scattering |
| MSD | Mean-Square Displacements |
| MSRD | Mean-Square Relative Displacements |
| Pair Distribution Function | |
| RMC | Reverse Monte Carlo |
References
- Özgür, U.; Alivov, Y.I.; Liu, C.; Teke, A.; Reshchikov, M.A.; Doğan, S.; Avrutin, V.; Cho, S.J.; Morkoç, H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98, 041301. [Google Scholar] [CrossRef] [Green Version]
- Janotti, A.; de Walle, C.G.V. Fundamentals of zinc oxide as a semiconductor. Rep. Prog. Phys. 2009, 72, 126501. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.M.; Lai, C.W.; Ngai, K.S.; Juan, J.C. Recent developments of zinc oxide based photocatalyst in water treatment technology: A review. Water Res. 2016, 88, 428–448. [Google Scholar] [CrossRef] [PubMed]
- Tereshchenko, A.; Bechelany, M.; Viter, R.; Khranovskyy, V.; Smyntyna, V.; Starodub, N.; Yakimova, R. Optical biosensors based on ZnO nanostructures: Advantages and perspectives. A review. Sens. Actuat. B-Chem. 2016, 229, 664–677. [Google Scholar] [CrossRef] [Green Version]
- Gurylev, V.; Perng, T.P. Defect engineering of ZnO: Review on oxygen and zinc vacancies. J. Eur. Ceram. Soc. 2021, 41, 4977–4996. [Google Scholar] [CrossRef]
- Rasmidi, R.; Duinong, M.; Chee, F.P. Radiation damage effects on zinc oxide (ZnO) based semiconductor devices—A review. Rad. Phys. Chem. 2021, 184, 109455. [Google Scholar] [CrossRef]
- Verma, R.; Pathak, S.; Srivastava, A.K.; Prawer, S.; Tomljenovic-Hanic, S. ZnO nanomaterials: Green synthesis, toxicity evaluation and new insights in biomedical applications. J. Alloys Compd. 2021, 876, 160175. [Google Scholar] [CrossRef]
- Abrahams, S.C.; Bernstein, J.L. Remeasurement of the structure of hexagonal ZnO. Acta Crystallogr. B 1969, 25, 1233–1236. [Google Scholar] [CrossRef]
- Reeber, R.R. Lattice parameters of ZnO from 4.2∘ to 296∘ K. J. Appl. Phys. 1970, 41, 5063–5066. [Google Scholar] [CrossRef]
- Karzel, H.; Potzel, W.; Köfferlein, M.; Schiessl, W.; Steiner, M.; Hiller, U.; Kalvius, G.M.; Mitchell, D.W.; Das, T.P.; Blaha, P.; et al. Lattice dynamics and hyperfine interactions in ZnO and ZnSe at high external pressures. Phys. Rev. B 1996, 53, 11425–11438. [Google Scholar] [CrossRef]
- Dal Corso, A.; Posternak, M.; Resta, R.; Baldereschi, A. Ab initio study of piezoelectricity and spontaneous polarization in ZnO. Phys. Rev. B 1994, 50, 10715–10721. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z. Novel nanostructures of ZnO for nanoscale photonics, optoelectronics, piezoelectricity, and sensing. Appl. Phys. A 2007, 88, 7–15. [Google Scholar] [CrossRef]
- Hsiao, C.C.; Huang, K.Y.; Hu, Y.C. Fabrication of a ZnO Pyroelectric Sensor. Sensors 2008, 8, 185–192. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bdikin, I.K.; Gracio, J.; Ayouchi, R.; Schwarz, R.; Kholkin, A.L. Local piezoelectric properties of ZnO thin films prepared by RF-plasma-assisted pulsed-laser deposition method. Nanotechnology 2010, 21, 235703. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Guo, W.; Pradel, K.C.; Zhu, G.; Zhou, Y.; Zhang, Y.; Hu, Y.; Lin, L.; Wang, Z.L. Pyroelectric Nanogenerators for Harvesting Thermoelectric Energy. Nano Lett. 2012, 12, 2833–2838. [Google Scholar] [CrossRef]
- Goel, S.; Kumar, B. A review on piezo-/ferro-electric properties of morphologically diverse ZnO nanostructures. J. Alloys Compd. 2020, 816, 152491. [Google Scholar] [CrossRef]
- Schulz, H.; Thiemann, K. Structure parameters and polarity of the wurtzite type compounds SiC-2H and ZnO. Solid State Commun. 1979, 32, 783–785. [Google Scholar] [CrossRef]
- Kihara, K.; Donnay, G. Anharmonic thermal vibrations in ZnO. Can. Mineral. 1985, 23, 647–654. [Google Scholar]
- Albertsson, J.; Abrahams, S.C.; Kvick, Å. Atomic displacement, anharmonic thermal vibration, expansivity and pyroelectric coefficient thermal dependences in ZnO. Acta Crystallogr. B 1989, 45, 34–40. [Google Scholar] [CrossRef]
- Serrano, J.; Manjón, F.J.; Romero, A.H.; Ivanov, A.; Cardona, M.; Lauck, R.; Bosak, A.; Krisch, M. Phonon dispersion relations of zinc oxide: Inelastic neutron scattering and ab initio calculations. Phys. Rev. B 2010, 81, 174304. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Lee, J.; Varshney, V.; Wohlwend, J.L.; Roy, A.K.; Luo, T. Thermal Conductivity of Wurtzite Zinc-Oxide from First-Principles Lattice Dynamics—A Comparative Study with Gallium Nitride. Sci. Rep. 2016, 6, 22504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Timoshenko, J.; Anspoks, A.; Kalinko, A.; Kuzmin, A. Temperature dependence of the local structure and lattice dynamics of wurtzite-type ZnO. Acta Mater. 2014, 79, 194–202. [Google Scholar] [CrossRef] [Green Version]
- Kuzmin, A.; Anspoks, A.; Kalinko, A.; Timoshenko, J. The use of X-ray absorption spectra for validation of classical force-field models. Z. Phys. Chem. 2016, 230, 537–549. [Google Scholar] [CrossRef]
- Lewis, G.V.; Catlow, C.R.A. Potential models for ionic oxides. J. Phys. C Solid State Phys. 1985, 18, 1149–1161. [Google Scholar] [CrossRef]
- Zaoui, A.; Sekkal, W. Pressure-induced softening of shear modes in wurtzite ZnO: A theoretical study. Phys. Rev. B 2002, 66, 174106. [Google Scholar] [CrossRef]
- Kulkarni, A.J.; Zhou, M.; Ke, F.J. Orientation and size dependence of the elastic properties of zinc oxide nanobelts. Nanotechnology 2005, 16, 2749–2756. [Google Scholar] [CrossRef] [Green Version]
- Klementiev, K.; Norén, K.; Carlson, S.; Clauss, K.G.V.S.; Persson, I. The BALDER Beamline at the MAX IV Laboratory. J. Phys. Conf. Ser. 2016, 712, 012023. [Google Scholar] [CrossRef] [Green Version]
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef] [Green Version]
- Kühne, T.D.; Iannuzzi, M.; Ben, M.D.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An Electronic Structure and Molecular Dynamics Software Package—Quickstep: Efficient and Accurate Electronic Structure Calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef]
- CP2K Developers Group. 2000–2021. Available online: https://www.cp2k.org (accessed on 5 August 2021).
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [Green Version]
- Krack, M. Pseudopotentials for H to Kr optimized for gradient-corrected exchange-correlation functionals. Theor. Chem. Acc. 2005, 114, 145–152. [Google Scholar] [CrossRef] [Green Version]
- VandeVondele, J.; Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar] [CrossRef] [Green Version]
- Kuzmin, A.; Timoshenko, J.; Kalinko, A.; Jonane, I.; Anspoks, A. Treatment of disorder effects in X-ray absorption spectra beyond the conventional approach. Rad. Phys. Chem. 2020, 175. [Google Scholar] [CrossRef] [Green Version]
- Bocharov, D.; Krack, M.; Rafalskij, Y.; Kuzmin, A.; Purans, J. Ab initio molecular dynamics simulations of negative thermal expansion in ScF3: The effect of the supercell size. Comput. Mater. Sci. 2020, 171, 109198. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar] [CrossRef] [Green Version]
- Dudarev, S.L.; Manh, D.N.; Sutton, A.P. Effect of Mott-Hubbard correlations on the electronic structure and structural stability of uranium dioxide. Philos. Mag. B 1997, 75, 613–628. [Google Scholar] [CrossRef]
- Rabone, J.; Krack, M. A procedure for bypassing metastable states in local basis set DFT+U calculations and its application to uranium dioxide surfaces. Comput. Mater. Sci. 2013, 71, 157–164. [Google Scholar] [CrossRef]
- Kuzmin, A.; Chaboy, J. EXAFS and XANES analysis of oxides at the nanoscale. IUCrJ 2014, 1, 571–589. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuzmin, A.; Evarestov, R.A. Quantum mechanics–molecular dynamics approach to the interpretation of X-ray absorption spectra. J. Phys. Condens. Matter 2009, 21, 055401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ankudinov, A.L.; Ravel, B.; Rehr, J.J.; Conradson, S.D. Real-space multiple-scattering calculation and interpretation of X-ray-absorption near-edge structure. Phys. Rev. B 1998, 58, 7565–7576. [Google Scholar] [CrossRef] [Green Version]
- Rehr, J.J.; Albers, R.C. Theoretical approaches to X-ray absorption fine structure. Rev. Mod. Phys. 2000, 72, 621–654. [Google Scholar] [CrossRef]
- Hedin, L.; Lundqvist, S. Explicit local exchange-correlation potentials. J. Phys. C Solid State Phys. 1971, 4, 2064. [Google Scholar] [CrossRef]
- Shalimov, A.; Paszkowicz, W.; Grasza, K.; Skupiński, P.; Mycielski, A.; Bak-Misiuk, J. X-ray characterisation of a bulk ZnO crystal. Phys. Status Solidi B 2007, 244, 1573–1577. [Google Scholar] [CrossRef]
- Booth, C.H.; Bridges, F.; Bauer, E.D.; Li, G.G.; Boyce, J.B.; Claeson, T.; Chu, C.W.; Xiong, Q. XAFS measurements of negatively correlated atomic displacements in HgBa2CuO4+δ. Phys. Rev. B 1995, 52, R15745. [Google Scholar] [CrossRef] [PubMed]
- Jeong, I.K.; Heffner, R.H.; Graf, M.J.; Bilinge, S.J.L. Lattice dynamics and correlated atomic motion from the atomic pair distribution function. Phys. Rev. B 2003, 67, 104301. [Google Scholar] [CrossRef] [Green Version]
- Sapelkin, A.V.; Bayliss, S.C. Distance dependence of mean-square relative displacements in EXAFS. Phys. Rev. B 2002, 65, 172104. [Google Scholar] [CrossRef]
- Jonane, I.; Lazdins, K.; Timoshenko, J.; Kuzmin, A.; Purans, J.; Vladimirov, P.; Gräning, T.; Hoffmann, J. Temperature-dependent EXAFS study of the local structure and lattice dynamics in cubic Y2O3. J. Synchrotron Rad. 2016, 23, 510–518. [Google Scholar] [CrossRef]
- Jonane, I.; Anspoks, A.; Kuzmin, A. Advanced approach to the local structure reconstruction and theory validation on the example of the W L3-edge extended X-ray absorption fine structure of tungsten. Model. Simul. Mater. Sci. Eng. 2018, 26, 025004. [Google Scholar] [CrossRef] [Green Version]
- Sevillano, E.; Meuth, H.; Rehr, J.J. Extended X-ray absorption fine structure Debye-Waller factors. I. Monatomic crystals. Phys. Rev. B 1979, 20, 4908–4911. [Google Scholar] [CrossRef]





| AIMD | Experiment | |||
|---|---|---|---|---|
| Temperature (K) | a (Å) | c (Å) | a (Å) | c (Å) |
| 300 | 3.258 | 5.220 | 3.24992 (5) | 5.20658 (8) |
| 600 | 3.265 | 5.231 | 3.25682 (5) | 5.21251 (8) |
| 900 | 3.272 | 5.243 | 3.26480 (5) | 5.21939 (8) |
| 1200 | 3.281 | 5.257 | ||
| T (K) | MSD (O) (Å) | MSD (Zn) (Å) |
|---|---|---|
| 300 | 0.0054 (4) | 0.0072 (4) |
| 600 | 0.010 (3) | 0.014 (3) |
| 900 | 0.018 (5) | 0.024 (5) |
| 1200 | 0.024 (6) | 0.033 (6) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bocharov, D.; Pudza, I.; Klementiev, K.; Krack, M.; Kuzmin, A. Study of High-Temperature Behaviour of ZnO by Ab Initio Molecular Dynamics Simulations and X-ray Absorption Spectroscopy. Materials 2021, 14, 5206. https://doi.org/10.3390/ma14185206
Bocharov D, Pudza I, Klementiev K, Krack M, Kuzmin A. Study of High-Temperature Behaviour of ZnO by Ab Initio Molecular Dynamics Simulations and X-ray Absorption Spectroscopy. Materials. 2021; 14(18):5206. https://doi.org/10.3390/ma14185206
Chicago/Turabian StyleBocharov, Dmitry, Inga Pudza, Konstantin Klementiev, Matthias Krack, and Alexei Kuzmin. 2021. "Study of High-Temperature Behaviour of ZnO by Ab Initio Molecular Dynamics Simulations and X-ray Absorption Spectroscopy" Materials 14, no. 18: 5206. https://doi.org/10.3390/ma14185206
APA StyleBocharov, D., Pudza, I., Klementiev, K., Krack, M., & Kuzmin, A. (2021). Study of High-Temperature Behaviour of ZnO by Ab Initio Molecular Dynamics Simulations and X-ray Absorption Spectroscopy. Materials, 14(18), 5206. https://doi.org/10.3390/ma14185206