Simulation of 3D Electrochemical Phase Formation: Mixed Growth Control
Abstract
:1. Introduction
2. Model and Calculation Method
3. Results and Discussion
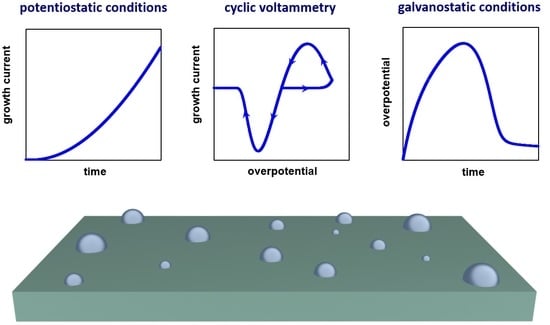
3.1. Potentiostatic Electrodeposition
3.2. Cyclic Voltammetry
3.3. Galvanostatic Electrodeposition
3.4. Example of Using the Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Staikov, G.; Milchev, A. The impact of electrocrystallization on nanotechnology. In Electrocrystallization in Nanotechnology; Staikov, G., Ed.; Wiley-VCH: Weinheim, Germany, 2007; pp. 1–29. [Google Scholar]
- Milchev, A. Electrocrystallization: Nucleation and growth of nano-clusters on solid surfaces. Russ. J. Electrochem. 2008, 44, 619–645. [Google Scholar] [CrossRef]
- Guo, L.; Oskam, G.; Radisic, A.; Hoffmann, P.M.; Searson, P.C. Island growth in electrodeposition. J. Phys. D Appl. Phys. 2011, 44, 443001. [Google Scholar] [CrossRef]
- Gunawardena, G.; Hills, G.J.; Montenegro, I.; Scharifker, B. Electrochemical nucleation: Part I. General considerations. J. Electroanal. Chem. 1982, 138, 225–239. [Google Scholar] [CrossRef]
- Scharifker, B.R.; Hills, G.J. Theoretical and experimental studies of multiple nucleation. Electrochim. Acta 1983, 28, 879–889. [Google Scholar] [CrossRef]
- Scharifker, B.R.; Mostany, J. Three-dimensional nucleation with diffusion controlled growth. Part I. Number density of active sites and nucleation rates per site. J. Electroanal. Chem. 1984, 177, 13–23. [Google Scholar] [CrossRef]
- Mirkin, M.V.; Nilov, A.P. Three-dimensional nucleation and growth under controlled potential. J. Electroanal. Chem. 1990, 283, 35–51. [Google Scholar] [CrossRef]
- Heerman, L.; Tarallo, A. Theory of the chronoamperometric transient for electrochemical nucleation with diffusion-controlled growth. J. Electroanal. Chem. 1999, 470, 70–76. [Google Scholar] [CrossRef]
- Sluyters-Rehbach, M.; Wijenberg, J.H.O.J.; Bosco, E.; Sluyters, J.H. The theory of chronoamperometry for the investigation of electrocrystallization. Mathematical description and analysis in the case of diffusion-controlled growth. J. Electroanal. Chem. 1987, 236, 1–20. [Google Scholar] [CrossRef]
- Hyde, M.E.; Compton, R.G. A review of the analysis of multiple nucleation with diffusion controlled growth. J. Electroanal. Chem. 2003, 549, 1–12. [Google Scholar] [CrossRef]
- Zapryanova, T.; Danilov, A.; Milchev, A. Growth kinetics of single copper crystals: The concentration dependence. Russ. J. Electrochem. 2010, 46, 607–610. [Google Scholar] [CrossRef]
- Radisic, A.; Vereecken, P.M.; Hannon, J.B.; Searson, P.C.; Ross, F.M. Quantifying electrochemical nucleation and growth of nanoscale clusters using real-time kinetic data. Nano Lett. 2006, 6, 238–242. [Google Scholar] [CrossRef]
- Brylev, O.; Roué, L.; Bélanger, D. Rhodium electrodeposition on pyrolytic graphite electrode: Analysis of chronoamperometric curves. J. Electroanal. Chem. 2005, 581, 22–30. [Google Scholar] [CrossRef]
- Kelaidopoulou, A.; Kokkinidis, G.; Milchev, A. Nucleation and growth of metal catalysts. Part I. Electrodeposition of platinum on tungsten. J. Electroanal. Chem. 1998, 444, 195–201. [Google Scholar] [CrossRef]
- Ustarroz, J.; Ke, X.; Hubin, A.; Bals, S.; Terryn, H. New Insights into the Early New Insights into the Early Stages of Nanoparticle Electrodeposition. J. Phys. Chem. C 2012, 116, 2322–2329. [Google Scholar] [CrossRef]
- Isaev, V.A.; Grishenkova, O.V.; Zaykov, Y.P. Analysis of the Geometrical–Probabilistic Models of Electrocrystallization. Russ. Met. 2016, 2016, 776–784. [Google Scholar] [CrossRef]
- Isaev, V.A.; Baraboshkin, A.N. Three-dimensional electrochemical phase formation. J. Electroanal. Chem. 1994, 377, 33–37. [Google Scholar] [CrossRef]
- Isaev, V.A.; Grishenkova, O.V.; Zaykov, Y.P. On the theory of 3D multiple nucleation with kinetic controlled growth. J. Electroanal. Chem. 2018, 818, 265–269. [Google Scholar] [CrossRef]
- Isaev, V.A.; Grishenkova, O.V.; Zaykov, Y.P.; Kosov, A.V.; Semerikova, O.L. Analysis of Potentiostatic Current Transients for Multiple Nucleation with Diffusion and Kinetic Controlled Growth. J. Electrochem. Soc. 2019, 166, D851–D856. [Google Scholar] [CrossRef]
- Correia, A.N.; Machado, S.A.S. Studies of Nickel Electrocrystallization on Platinum Ultramicroelectrodes. J. Braz. Chem. Soc. 1997, 8, 71–76. [Google Scholar] [CrossRef] [Green Version]
- Milchev, A. Nucleation and growth of clusters through multi-step electrochemical reactions. J. Electroanal. Chem. 2008, 612, 42–46. [Google Scholar] [CrossRef]
- Milchev, A.; Zapryanova, T. Nucleation and growth of copper under combined charge transfer and diffusion limitations: Part I. Electrochim. Acta 2006, 51, 2926–2933. [Google Scholar] [CrossRef]
- Milchev, A.; Zapryanova, T. Nucleation and growth of copper under combined charge transfer and diffusion limitations: Part II. Electrochim. Acta 2006, 51, 4916–4921. [Google Scholar] [CrossRef]
- Altimari, P.; Pagnanelli, F. Electrochemical nucleation and three-dimensional growth under mixed kinetic-diffusion control: Analytical approximation of the current transient. Electrochim. Acta 2016, 205, 113–117. [Google Scholar] [CrossRef]
- Altimari, P.; Pagnanelli, F. Electrochemical nucleation and three-dimensional growth of metal nanoparticles under mixed kinetic-diffusion control: Model development and validation. Electrochim. Acta 2016, 206, 116–126. [Google Scholar] [CrossRef]
- Rezaei, M.; Tabaian, S.H.; Haghshenas, D.F. A kinetic description of Pd electrodeposition under mixed control of charge transfer and diffusion. J. Electroanal. Chem. 2012, 687, 95–101. [Google Scholar] [CrossRef]
- Pritzker, M.D. Voltammetric response for the diffusion controlled electrodeposition onto growing hemispherical nuclei. J. Electroanal. Chem. 1988, 243, 57–80. [Google Scholar] [CrossRef]
- Abyaneh, M.Y.; Fleischmann, M.; Mehrabi, M.H. Modelling the growth of a single centre. J. Electroanal. Chem. 2019, 834, 114–123. [Google Scholar] [CrossRef]
- Velmurugan, J.; Noёl, J.-M.; Nogala, W.; Mirkin, M.V. Nucleation and growth of metal on nanoelectrodes. Chem. Sci. 2012, 3, 3307–3314. [Google Scholar] [CrossRef]
- Velmurugan, J.; Noёl, J.-M.; Mirkin, M.V. Nucleation and growth of mercury on Pt nanoelectrodes at different overpotentials. Chem. Sci. 2014, 5, 189–194. [Google Scholar] [CrossRef]
- Fletcher, S.; Halliday, C.S.; Gates, D.; Westcott, M.; Lwin, T.; Nelson, G. The response of some nucleation/growth processes to triangular scans of potential. J. Electroanal. Chem. 1983, 159, 267–285. [Google Scholar] [CrossRef]
- Isaev, V.A.; Grishenkova, O.V.; Kosov, A.V.; Semerikova, O.L.; Zaykov, Y.P. On the theory of cyclic voltammetry for formation and growth of single metal cluster. J. Solid State Electrochem. 2017, 21, 787–791. [Google Scholar] [CrossRef]
- Mamme, M.H.; Deconinck, J.; Ustarroz, J. Transition between kinetic and diffusion control during the initial stages of electrochemical growth using numerical modelling. Electrochim. Acta 2017, 258, 662–668. [Google Scholar] [CrossRef]
- Mamme, M.H.; Cherigui, E.A.M.; Dolgikh, O.; Ustarroz, J.; Simillion, H.; Terryn, H.; Deconinck, J. A Finite Element Simulation of the Electrochemical Growth of a Single Hemispherical Silver Nucleus. Electrochim. Acta 2016, 197, 307–317. [Google Scholar] [CrossRef]
- Frenkel, Y.I. Kinetic Theory of Liquids; Oxford University Press: Oxford, UK, 1946. [Google Scholar]
- Isaev, V.A. Electrochemical Phase Formation; UB, Russian Academy of Science: Ekaterinburg, Russia, 2007. (In Russian) [Google Scholar]
- Isaev, V.A.; Grishenkova, O.V. Kinetics of electrochemical nucleation and growth. Electrochem. Comm. 2001, 3, 500–504. [Google Scholar] [CrossRef]
- Hills, G.J.; Schiffrin, D.J.; Thompson, J. Electrochemical nucleation from molten salts—I. Diffusion controlled electrodeposition of silver from alkali molten nitrates. Electrochim. Acta 1974, 19, 657–670. [Google Scholar] [CrossRef]
- Fletcher, S. Electrochemical deposition of hemispherical nuclei under diffusion control. Some theoretical considerations. J. Chem. Soc. Faraday Trans. 1 1983, 79, 467–479. [Google Scholar] [CrossRef]
- Fletcher, S. Some formulae describing spherical and hemispherical diffusion to small crystals in unstirred solutions. J. Cryst. Growth 1983, 62, 505–512. [Google Scholar] [CrossRef]
- Milchev, A.; Montenegro, M.I. A galvanostatic study of electrochemical nucleation. J. Electroanal. Chem. 1992, 333, 93–102. [Google Scholar] [CrossRef]
- Isaev, V.A.; Grishenkova, O.V. Galvanostatic nucleation and growth under diffusion control. J. Solid State Electrochem. 2013, 17, 1505–1508. [Google Scholar] [CrossRef]
- Isaev, V.A.; Grishenkova, O.V. Galvanostatic phase formation. J. Solid State Electrochem. 2014, 18, 2383–2386. [Google Scholar] [CrossRef]
- Baraboshkin, A.N. Electrocrystallization of Metals from Molten Salts; Nauka: Moscow, Russia, 1976. (In Russian) [Google Scholar]
- Grishenkova, O.V.; Zaykov, Y.P.; Isaev, V.A. Computer Simulation of the Initial Stages of Electrocrystallization during Cyclic Potential Sweep. Russ. Met. 2020, 2020, 107–111. [Google Scholar] [CrossRef]
- Isaev, V.A.; Grishenkova, O.V.; Kosov, A.V.; Semerikova, O.L.; Zaykov, Y.P. Simulation of the potentiodynamic and galvanostatic phase formation in the melts. Russ. Met. 2017, 2017, 146–151. [Google Scholar] [CrossRef]
- Grishenkova, O.V.; Isaev, V.A. The formation of nano- and microcrystals during electrodeposition II. Background melt. Rasplavy 2009, 5, 65–70. (In Russian) [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isaev, V.A.; Grishenkova, O.V.; Kosov, A.V.; Semerikova, O.L.; Zaikov, Y. Simulation of 3D Electrochemical Phase Formation: Mixed Growth Control. Materials 2021, 14, 6330. https://doi.org/10.3390/ma14216330
Isaev VA, Grishenkova OV, Kosov AV, Semerikova OL, Zaikov Y. Simulation of 3D Electrochemical Phase Formation: Mixed Growth Control. Materials. 2021; 14(21):6330. https://doi.org/10.3390/ma14216330
Chicago/Turabian StyleIsaev, Vladimir A., Olga V. Grishenkova, Alexander V. Kosov, Olga L. Semerikova, and Yuriy Zaikov. 2021. "Simulation of 3D Electrochemical Phase Formation: Mixed Growth Control" Materials 14, no. 21: 6330. https://doi.org/10.3390/ma14216330
APA StyleIsaev, V. A., Grishenkova, O. V., Kosov, A. V., Semerikova, O. L., & Zaikov, Y. (2021). Simulation of 3D Electrochemical Phase Formation: Mixed Growth Control. Materials, 14(21), 6330. https://doi.org/10.3390/ma14216330