An Innovative Approach of Parameter Loading Path Design for Grain Refinement and Its Application in Ni80A Superalloy
Abstract
:1. Introduction
2. Basis Theory of Deformation Mechanism Map
3. Clarification of Grain Refinement Domains
3.1. Elaboration of Deformation Mechanisms
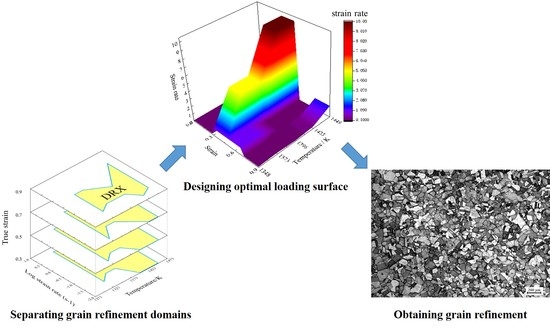
3.2. Separation and Discretization of Grain Refinement Domains
4. Design in Optimal Parameter–Loading paths
4.1. Design Procedures of Optimal Parameter–Loading Path
4.2. Descriptions of Optimal Parameter Loading Path
4.3. Fitting Optimal Parameter Loading Path
4.4. Verifications of Optimal Parameter Loading Path
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pollock, T.M.; Tin, S. Nickel-based superalloys for advanced turbine engines: Chemistry, microstructure and properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar] [CrossRef]
- Kim, D.K.; Kim, D.Y.; Ryu, S.H.; Kim, D.J. Application of Nimonic 80A to the hot forging of an exhaust valve head. J. Mater. Process. Technol. 2001, 113, 148–152. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, C.; Xiao, X.; Cao, X.; Jia, G.; Shen, Z. Evolution of microstructure and mechanical properties of Ti modified superalloy Nimonic 80A. Mater. Sci. Eng. A 2011, 530, 315–326. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhimin, Y.; Jiangpin, X. Microstructural mapping in closed die forging process of superalloy Nimonic 80a valve head. J. Alloys Compd. 2011, 509, 6106–6112. [Google Scholar] [CrossRef]
- Jeong, H.; Cho, J.; Park, H. Microstructure prediction of Nimonic 80A for large exhaust valve during hot closed die forging. J. Mater. Process. Technol. 2005, 162, 504–511. [Google Scholar] [CrossRef]
- Saikrishna, N.; Reddy, G.P.K.; Munirathinam, B.; Sunil, B.R. Influence of bimodal grain size distribution on the corrosion behavior of friction stir processed biodegradable AZ31 magnesium alloy. J. Magnes. Alloys 2016, 4, 68–76. [Google Scholar] [CrossRef] [Green Version]
- Sani, S.A.; Ebrahimi, G.; Rashid, A.K. Hot deformation behavior and dynamic recrystallization kinetics of AZ61 and AZ61 + Sr magnesium alloys. J. Magnes. Alloys 2016, 4, 104–114. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhang, X.; Lu, X.; Yang, Y.; Wang, Z. Microstructure, texture and mechanical properties of hot-rolled Mg–4Al–2Sn–0.5 Y–0.4 Nd alloy. J. Magnes. Alloys 2016, 4, 207–213. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.C.; Lin, Y.C.; Deng, J.; Liu, G.; Chen, M.S. Hot tensile deformation behaviors and constitutive model of 42CrMo steel. Mater. Des. 2014, 53, 349–356. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, W.; Zhen, L.; Zhang, X. Microstructure evolution during dynamic recrystallization of hot deformed superalloy 718. Mater. Sci. Eng. A 2008, 486, 321–332. [Google Scholar] [CrossRef]
- Bhujangrao, T.; Froustey, C.; Iriondo, E.; Veiga, F.; Darnis, P.; Mata, F.G. Review of Intermediate Strain Rate Testing Devices. Metals 2020, 10, 894. [Google Scholar] [CrossRef]
- Bhujangrao, T.; Veiga, F.; Suárez, A.; Iriondo, E.; Mata, F.G. High-Temperature Mechanical Properties of IN718 Alloy: Comparison of Additive Manufactured and Wrought Samples. Crystals 2020, 10, 689. [Google Scholar] [CrossRef]
- Quan, G.Z.; Zhang, L.; Wang, X. Evolution of grain refinement degree induced by dynamic recrystallization for Nimonic 80A during hot compression process and its FEM analysis. Vacuum 2017, 139, 51–63. [Google Scholar] [CrossRef]
- Quan, G.Z.; Pan, J.; Wang, X.; Zhang, Z.H.; Zhang, L.; Wang, T. Correspondence between grain refinements and flow softening behaviors at Nimonic 80A superalloy under different strain rates, temperatures and strains. Mater. Sci. Eng. A 2017, 679, 358–371. [Google Scholar] [CrossRef]
- Quan, G.Z.; Qiao, L.; Jiang, Z.; Xiong, W.; Shi, R.J. Determination of dynamic recrystallization parameter domains of Ni80A superalloy by enhanced processing maps. Trans. Nonferrous Met. Soc. China 2019, 29, 1449–1464. [Google Scholar] [CrossRef]
- Wen, D.X.; Lin, Y.C.; Li, H.B.; Chen, X.M.; Deng, J.; Li, L.T. Hot deformation behavior and processing map of a typical Ni-based superalloy. Mater. Sci. Eng. A 2014, 591, 183–192. [Google Scholar] [CrossRef]
- Łukaszek-Sołek, A.; Śleboda, T.; Krawczyk, J.; Bednarek, S.; Wojtaszek, M. Characterization of the workability of Ni-Fe-Mo alloy by complex processing maps. J. Alloys Compd. 2019, 797, 174–184. [Google Scholar] [CrossRef]
- Mokdad, F.; Chen, D.L.; Liu, Z.Y.; Ni, D.R.; Xiao, B.L.; Ma, Z.Y. Three-dimensional processing maps and microstructural evolution of a CNT-reinforced Al−Cu−Mg nanocomposite. Mater. Sci. Eng. A 2017, 702, 425–437. [Google Scholar] [CrossRef]
- Quan, G.Z.; Zhao, L.; Chen, T.; Wang, Y.; Mao, Y.P.; Lv, W.Q.; Zhou, J. Identification for the optimal working parameters of as-extruded 42CrMo high-strength steel from a large range of strain, strain rate and temperature. Mater. Sci. Eng. A 2012, 538, 364–373. [Google Scholar] [CrossRef]
- Jiang, H.; Dong, J.; Zhang, M.; Zheng, L.; Yao, Z. Hot deformation characteristics of Alloy 617B nickel-based superalloy: A study using processing map. J. Alloys Compd. 2015, 647, 338–350. [Google Scholar] [CrossRef]
- Park, N.K.; Yeom, J.T.; Na, Y.S. Characterization of deformation stability in hot forging of conventional Ti–6Al–4V using processing maps. J. Mater. Process. Technol. 2002, 130, 540–545. [Google Scholar] [CrossRef]
- Quan, G.Z.; Pan, J.; Wang, X.; Zhang, Z.H.; Zhang, L.; Wang, T. Phase transformation and recrystallization kinetics in space–time domain during isothermal compressions for Ti–6Al–4V analyzed by multi-field and multi-scale coupling FEM. Mater. Des. 2016, 94, 523–535. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Gegel, H.L.; Doraivelu, S.M.; Malas, J.C.; Morgan, J.T.; Lark, K.A.; Barker, D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Met. Trans. A 1984, 15, 1883–1892. [Google Scholar] [CrossRef]
- Liu, J.; Cui, Z.; Li, C. Analysis of metal workability by integration of FEM and 3-D processing maps. J. Mater. Process. Technol. 2008, 205, 497–505. [Google Scholar] [CrossRef]
- Pu, E.; Zheng, W.; Song, Z.; Feng, H.; Dong, H. Hot deformation characterization of nickel-based superalloy UNS10276 through processing map and microstructural studies. J. Alloys Compd. 2017, 694, 617–631. [Google Scholar] [CrossRef]




















| True Strain | Domain | Parameter Range | ||
|---|---|---|---|---|
| Temperature (K) | Strain Rate (s−1) | Peak η-Value | ||
| 0.3 | DOM#1–0.2 | 1300–1473 | 1.00–3.55 | 0.37 |
| DOM#2–0.2 | 1273–1473 | 0.01–1.00 | 0.50 | |
| 0.5 | DOM#1–0.4 | 1298–1473 | 1.00–5.01 | 0.38 |
| DOM#2–0.4 | 1273–1473 | 0.01–1.00 | 0.42 | |
| 0.7 | DOM#1–0.6 | 1273–1430 | 0.01–0.79 | 0.42 |
| DOM#2–0.6 | 1430–1473 | 0.01–3.16 | 0.40 | |
| 0.9 | DOM#1–0.8 | 1310–1415 | 0.01–0.25 | 0.44 |
| DOM#2–0.8 | 1415–1473 | 0.04–0.79 | 0.40 | |
| Stage | Temperature (K) | ||||
|---|---|---|---|---|---|
| 1348 | 1373 | 1398 | 1423 | 1448 | |
| I | 0.06–4.47 | 0.06–3.16 | 0.01–10.00 | 0.01–10.00 | 0.01–10.00 |
| II | 0.03–5.62 | 0.03–5.62 | 0.01–5.62 | 0.01–10.00 | 0.01–10.00 |
| III | 0.07–1.41 | 0.07–1.20 | 0.02–1.00 | 0.01–1.58 | 0.01–3.16 |
| IV | 0.07–0.56 | 0.07–0.35 | 0.07–0.18 | 0.02–0.50 | 0.03–1.78 |
| T/°C | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
|---|---|---|---|---|---|---|---|---|---|
| k/(N/s) | 12.11 | 13.83 | 15.48 | 16.75 | 18.39 | 20.93 | 24.48 | 25.57 | 27.76 |
| T/°C | 20 | 200 | 400 | 600 | 800 | 900 | 1000 |
|---|---|---|---|---|---|---|---|
| E/Pa | 219,000 | 210,000 | 197,000 | 183,000 | 165,000 | 153,000 | 141,000 |
| Stage | Temperature (K) | ||||
|---|---|---|---|---|---|
| 1348 | 1373 | 1398 | 1423 | 1448 | |
| I | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| II | 1 | 5 | 5 | 10 | 10 |
| III | 1 | 1 | 0.1 | 0.1 | 0.1 |
| IV | 0.1 | 0.2 | 0.1 | 0.3 | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, G.-Z.; Yu, Y.-Z.; Sheng, X.; Yang, K.; Xiong, W. An Innovative Approach of Parameter Loading Path Design for Grain Refinement and Its Application in Ni80A Superalloy. Materials 2021, 14, 6703. https://doi.org/10.3390/ma14216703
Quan G-Z, Yu Y-Z, Sheng X, Yang K, Xiong W. An Innovative Approach of Parameter Loading Path Design for Grain Refinement and Its Application in Ni80A Superalloy. Materials. 2021; 14(21):6703. https://doi.org/10.3390/ma14216703
Chicago/Turabian StyleQuan, Guo-Zheng, Yan-Ze Yu, Xue Sheng, Kun Yang, and Wei Xiong. 2021. "An Innovative Approach of Parameter Loading Path Design for Grain Refinement and Its Application in Ni80A Superalloy" Materials 14, no. 21: 6703. https://doi.org/10.3390/ma14216703
APA StyleQuan, G. -Z., Yu, Y. -Z., Sheng, X., Yang, K., & Xiong, W. (2021). An Innovative Approach of Parameter Loading Path Design for Grain Refinement and Its Application in Ni80A Superalloy. Materials, 14(21), 6703. https://doi.org/10.3390/ma14216703