Compressive and Tensile Elastic Properties of Concrete: Empirical Factors in Span Reinforced Structures Design
Abstract
:1. Introduction
- 1.
- the viscoelastic character of concrete deforming under load;
- 2.
- equal deforming under equal stresses;
- 3.
- three-line model of non-linear deforming under load.
- 4.
- axial compression deformation test;
- 5.
- calculated by the multi-scale model and homogeneity theory based on the micro-elastic properties by the nanoindentation test;
- 6.
- evaluated by the relationship between the compressive strength or the dynamic elastic modulus and the static elastic modulus;
- 7.
- use of ultrasonic waves.
- Research the concrete deformability on standard beam samples with the equal strength of concrete and different elastic properties under compression and bending tensile;
- Research the deformations of concrete beams, reinforced by steel and composite, under bending load;
- Modelling and deflection calculation of the same beams under the same load conditions;
- Estimation of elasticity modulus increasing effectiveness in bending reinforced concrete elements exploitation.
2. Materials and Methods
- the HWC B25 with normal elasticity modulus E = 30,000 MPa (concrete 1);
- the HWC B25 with increased elasticity modulus E = 33,000 MPa due to fractioned coarse aggregate 10–20 mm (concrete 2);
- the LWC B15 D1600 with E = 15,000 MPa on the base of expanded clay gravel and quartz sand (concrete 3);
- the LWC B7.5 D1000 with E = 5000 MPa on the base of expanded clay gravel and perlite sand (concrete 4).
3. Results and Discussion
3.1. Research of the Standard Sample Concrete Beam Deformability with Different Elastic Properties under Compression and Tensile Bending
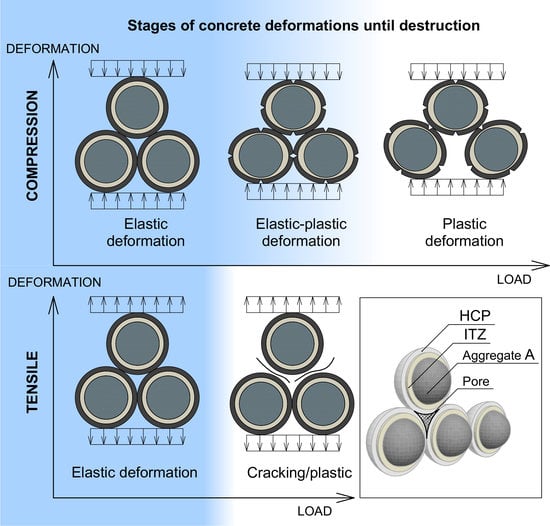
- Plastic deformations under compression on the load stages delay begin to develop already after reaching 20% of breaking load, and with the load increasing plastic deformations’ part grows, and total modulus of deformation degrades in arithmetical progression keeping instantaneous elasticity modulus;
- Plastic deformations under tensile bending are minimal and do not develop until concrete destruction;
- Plastic deformations of concrete on porous aggregates are much less compared to heavyweight concretes.
3.2. Research of Concrete Sample Beams Reinforced by Steel and Composite under Bending Tensile
4. Conclusions
- Concrete tensile deformations’ character is elastic, not depending on the load level in contrast with the viscoelastic character of deformations under compression. The concrete deformations’ models under compression and tensile are proposed.
- The three-line deformation model of span structures is ineffective. This model exceeds calculated deflections and over reinforcement in span structures design. The elastic two-line model is more applicable than the three-line deformation model.
- Instantaneous elastic deformations under compression are much lower than tensile. Prolonged elastic deformations under compression are close to tensile. It results in compressive elasticity modulus exceeding the tensile. The relation between these moduli is proposed. The relation provides operative elasticity modulus testing by the bending tensile method.
- The elasticity modulus’s evaluation for the reinforced span structures could be based only on the bending testing results. A 10% elasticity modulus increase, which seems not significant, increases at 30–40% the stress of the reinforced span structures under load and 30% increases the cracking point stress.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yoshitake, I.; Rajabipour, F.; Mimura, Y.; Scanlon, A. A Prediction Method of Tensile Young’s Modulus of Concrete at Early Age. Adv. Civ. Eng. 2012, 2012, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Ekin, N.; Uyanik, O. Comparison of Static and Dynamic Elastic Moduli in Concrete: Effects of Compressive Strength, Curing Conditions and Reinforcement. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 2327–2343. [Google Scholar] [CrossRef]
- Makridin, N.I.; Kalachnikov, V.I.; Maksimova, I.N.; Tarakanov, O.V.; Polubarova, J.V. Inner friction and dynamic modulus of elasticity of structural concrete. J. Eng. Appl. Sci. 2016, 11, 1545–1548. [Google Scholar] [CrossRef]
- Amer, I.; Kohail, M.; El-Feky, M.S.; Rashad, A.; Khalaf, M.A. A review on alkali-activated slag concrete. Ain Shams Eng. J. 2021, 12, 1475–1499. [Google Scholar] [CrossRef]
- Liu, B.D.; Lv, W.J.; Li, L.; Li, P.F. Effect of moisture content on static compressive elasticity modulus of concrete. Constr. Build. Mater. 2014, 69, 133–142. [Google Scholar] [CrossRef]
- Hadjab, H.; Arbia, A.; Boulekfouf, O. The use of ultrasonic waves and analytical modeling to estimate elasticity modulus of rubber concrete specimen. Adv. Struct. Mater. 2014, 54, 49–57. [Google Scholar] [CrossRef]
- Sideris, K.K.; Manita, P.; Sideris, K. Estimation of ultimate modulus of elasticity and Poisson ratio of normal concrete. Cem. Concr. Compos. 2004, 26, 623–631. [Google Scholar] [CrossRef]
- Brooks, J.J. Concrete and Masonry Movements; Elsevier Inc.: Amsterdam, The Netherlands, 2014; ISBN 9780128017678. [Google Scholar]
- Tibbetts, C.M.; Perry, M.C.; Ferraro, C.C.; Hamilton, H.R. (Trey) Aggregate Correction Factors for Concrete Elastic Modulus Prediction. ACI Struct. J. 2018, 115. [Google Scholar] [CrossRef]
- Yildirim, H.; Sengul, O. Modulus of elasticity of substandard and normal concretes. Constr. Build. Mater. 2011, 25, 1645–1652. [Google Scholar] [CrossRef]
- Zhu, X.; Gao, Y.; Dai, Z.; Corr, D.J.; Shah, S.P. Effect of interfacial transition zone on the Young’s modulus of carbon nanofiber reinforced cement concrete. Cem. Concr. Res. 2018, 107, 49–63. [Google Scholar] [CrossRef]
- Medina, C.; Zhu, W.; Howind, T.; De Rojas, M.I.S.; Frías, M. Influence of interfacial transition zone on engineering properties of the concrete manufactured with recycled ceramic aggregate. J. Civ. Eng. Manag. 2015, 21, 83–93. [Google Scholar] [CrossRef] [Green Version]
- Zouaoui, R.; Miled, K.; Limam, O.; Beddey, A. Analytical prediction of aggregates’ effects on the ITZ volume fraction and Young’s modulus of concrete. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 976–993. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, Z.; Lin, J.; Xu, W.; Liu, L. Numerical modeling on the influence of particle shape on ITZ’s microstructure and macro-properties of cementitious composites: A critical review. J. Sustain. Cem. Mater. 2018, 7, 248–269. [Google Scholar] [CrossRef]
- Sadowski, G.; Jaskulski, R. Comparative analysis of dependence of the elastic modulus of concrete on its composition. Mater. Struct. Technol. 2018, 1, 1–9. [Google Scholar] [CrossRef]
- Sanahuja, J.; Dormieux, L.; Chanvillard, G. Modelling elasticity of a hydrating cement paste. Cem. Concr. Res. 2007, 37, 1427–1439. [Google Scholar] [CrossRef]
- Fládr, J.; Bílý, P.; Trtík, T. Analysis of the influence of supplementary cementitious materials used in UHPC on modulus of elasticity. IOP Conf. Ser. Mater. Sci. Eng. 2019, 522, 012010. [Google Scholar] [CrossRef]
- Topçu, I.B.; Bilir, T.; Boǧa, A.R. Estimation of the modulus of elasticity of slag concrete by using composite material models. Constr. Build. Mater. 2010, 24, 741–748. [Google Scholar] [CrossRef]
- Noguchi, T.; Tomosawa, F. Relationship between Compressive Strength and Modulus of Elasticity of High Strength Concrete. J. Struct. Constr. Eng. 1995, 60, 1–10. [Google Scholar] [CrossRef]
- Silva, R.V.; De Brito, J.; Dhir, R.K. Establishing a relationship between modulus of elasticity and compressive strength of recycled aggregate concrete. J. Clean. Prod. 2016, 112, 2171–2186. [Google Scholar] [CrossRef]
- Jurowski, K.; Grzeszczyk, S. The Influence of Concrete Composition on Young’s Modulus. Procedia Eng. 2015, 108, 584–591. [Google Scholar] [CrossRef] [Green Version]
- Alsalman, A.; Dang, C.N.; Prinz, G.S.; Hale, W.M. Evaluation of modulus of elasticity of ultra-high performance concrete. Constr. Build. Mater. 2017, 153, 918–928. [Google Scholar] [CrossRef]
- Ferdous, W.; Manalo, A.; Siddique, R.; Mendis, P.; Zhuge, Y.; Wong, H.S.; Lokuge, W.; Aravinthan, T.; Schubel, P. Recycling of landfill wastes (tyres, plastics and glass) in construction—A review on global waste generation, performance, application and future opportunities. Resour. Conserv. Recycl. 2021, 173, 105745. [Google Scholar] [CrossRef]
- Siddika, A.; Hajimohammadi, A.; Al Mamun, M.A.; Alyousef, R.; Ferdous, W. Waste glass in cement and geopolymer concretes: A review on durability and challenges. Polymers 2021, 13, 2071. [Google Scholar] [CrossRef]
- De Avila Jacintho, A.E.P.G.; Cavaliere, I.S.G.; Pimentel, L.L.; Forti, N.C.S. Modulus and strength of concretes with alternative materials. Materials 2020, 13, 1–21. [Google Scholar] [CrossRef]
- Hunka, P.; Kolisko, J.; Vokac, M.; Rehacek, S. Test and Technological Influences on Modulus of Elasticity of Concrete—Recapitulation. Procedia Eng. 2013, 65, 266–272. [Google Scholar] [CrossRef] [Green Version]
- Vakhshouri, B. Modulus of Elasticity of Concrete in Design Codes and Empirical Models: Analytical Study. Pract. Period. Struct. Des. Constr. 2018, 23, 04018022. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, G.; Liu, H.; Huang, Y. Creep damage model considering unilateral effect based on bimodulus theory. Int. J. Damage Mech. 2021, 30. [Google Scholar] [CrossRef]
- Ambartsumyan, S.A.; Khachatryan, A.A. Basic Equations in the Theory of Elasticity for Materials with Different Stiffness in Tension and Compression (English translation available from The Aerospace Corp., El Segundo, Calif., as LRG-67-T-12). Inzhenernyi Zhurnal Mekhanika Tverd. Tela 1966, 1, 44–53. [Google Scholar]
- Russian State Standards GOST 24452-80 “Concretes. Methods of Prismatic, Compressive Strength, Modulus of Elasticity and Poisson’s Ratio Determination”. Available online: https://docs.cntd.ru/document/9056198 (accessed on 21 November 2021).
- Russian State Standards GOST 22690-2015 “Concretes. Determination of Strength by Mechanical Methods of Nondestructive Testing”. Available online: https://docs.cntd.ru/document/1200124396 (accessed on 21 November 2021).
- Russian State Standard GOST 310.4-81* “Cements. Methods of bending and compression strength determination”. Available online: https://docs.cntd.ru/document/871001227 (accessed on 21 November 2021).
- Korolev, A.; Vatin, N. Elasticity modulus of cement composites predicting using layer structure model. Mag. Civ. Eng. 2021, 104, 10413. [Google Scholar] [CrossRef]
- Contact and Crack Problems in Linear Theory of Elasticity; Bentham Science Publishers: Sharjah, United Arab Emirates, 2010. [CrossRef]
- Sun, J.Y.; Zhu, H.Q.; Qin, S.H.; Yang, D.L.; He, X. ting A review on the research of mechanical problems with different moduli in tension and compression. J. Mech. Sci. Technol. 2010, 24, 1845–1854. [Google Scholar] [CrossRef]
- Jones, R.M. Stress-strain relations for materials with different moduli in tension and compression. AIAA J. 1977, 15, 16–23. [Google Scholar] [CrossRef]
- Yao, W.J.; Ye, Z.M. Analytical solution of bending-compression column using different tension-compression modulus. Appl. Math. Mech. 2004, 25, 983–993. [Google Scholar] [CrossRef]













| N° | Modulus of Elasticity under Compression Ec, MPa | Modulus of Deformation under Compression Ecd, MPa | Modulus of Elasticity under Bending Tensile Ebt, MPa | Modulus of Deformation under Bending Tensile Ebtd, MPa |
|---|---|---|---|---|
| 1 | 30,000 | 18,000 | 2900 | 2600 |
| 2 | 33,000 | 20,800 | 3375 | 3000 |
| 3 | 15,180 | 14,500 | 1550 | 1550 |
| 4 | 5800 | 5800 | 1100 | 1050 |
| HCP | 50,000 | - | 5860 | - |
| Concrete N°/Reinforcement | Bending Tensile Modulus of the Reinforced Beam, MPa | Calculated Deflection, mm | Fact Deflection, mm | Deflection Provision, % |
|---|---|---|---|---|
| 1/steel | 13,400 | 3.39 | 1.41 | 140 |
| 1/composite | 7200 | 9.74 | 1.80 | 441 |
| 2/steel | 14,500 | 3.34 | 1.37 | 144 |
| 2/composite | 8500 | 9.59 | 1.57 | 510 |
| 3/steel | 9100 | 3.09 | 0.67 | 361 |
| 3/composite | 6200 | 4.30 | 0.79 | 544 |
| 4/steel | 5900 | 4.75 | 1.35 | 251 |
| 4/composite | 3300 | 12.1 | 4.12 | 294 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korolev, A.S.; Kopp, A.; Odnoburcev, D.; Loskov, V.; Shimanovsky, P.; Koroleva, Y.; Vatin, N.I. Compressive and Tensile Elastic Properties of Concrete: Empirical Factors in Span Reinforced Structures Design. Materials 2021, 14, 7578. https://doi.org/10.3390/ma14247578
Korolev AS, Kopp A, Odnoburcev D, Loskov V, Shimanovsky P, Koroleva Y, Vatin NI. Compressive and Tensile Elastic Properties of Concrete: Empirical Factors in Span Reinforced Structures Design. Materials. 2021; 14(24):7578. https://doi.org/10.3390/ma14247578
Chicago/Turabian StyleKorolev, Alexander Sergeevich, Anastasia Kopp, Denis Odnoburcev, Vladislav Loskov, Pavel Shimanovsky, Yulia Koroleva, and Nikolai Ivanovich Vatin. 2021. "Compressive and Tensile Elastic Properties of Concrete: Empirical Factors in Span Reinforced Structures Design" Materials 14, no. 24: 7578. https://doi.org/10.3390/ma14247578
APA StyleKorolev, A. S., Kopp, A., Odnoburcev, D., Loskov, V., Shimanovsky, P., Koroleva, Y., & Vatin, N. I. (2021). Compressive and Tensile Elastic Properties of Concrete: Empirical Factors in Span Reinforced Structures Design. Materials, 14(24), 7578. https://doi.org/10.3390/ma14247578