Study on a Hexagonal Acoustic Metamaterial Cell of Multiple Parallel-Connection Resonators with Tunable Perforating Rate
Abstract
:1. Introduction
2. Materials and Methods
2.1. Structural Design
2.2. Theoretical Model
2.3. Finite Element Simulation
2.4. Parameter Optimization
2.5. Sample Fabrication
2.6. Sound Absorption Coefficient Detection
3. Results and Discussions
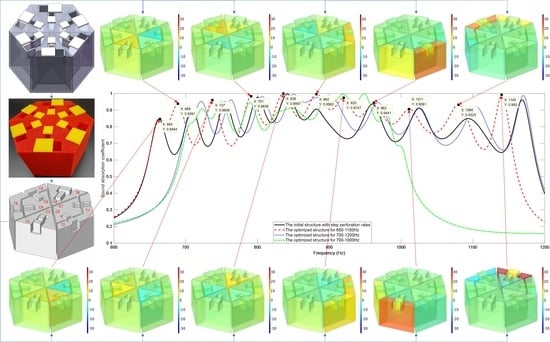
3.1. Comparative Analysis
3.2. Sound Absorption Mechanism
4. Conclusions
- (1)
- The hexagonal acoustic metamaterial cell consisting of six triangular cavities and six trapezium cavities was proposed, and the perforation rate of each cavity was adjustable by moving the sliding block along the slideway in the cavity. The acoustic metamaterial with tunable sound absorption performance was developed by this method, and the optional ranges of length of the aperture were 6–11.17 mm for the triangular cavity and 6.94–14.14 mm for the trapezium cavity.
- (2)
- The optimal geometric parameters of length of the apertures were obtained by the joint optimization of the acoustic finite element simulation and cuckoo search algorithm, and the average sound absorption coefficients in the target frequency ranges of 650–1150 Hz, 700–1200 Hz and 700–1000 Hz were 0.8565, 0.8615 and 0.8807, respectively, which exhibited an excellent tunable sound absorption performance.
- (3)
- The experimental sample for the hexagonal acoustic metamaterial cell was fabricated by the fused filament fabrication method, which included the chamber, rear panel, six sliding blocks for the triangular cavity and six sliding blocks for the trapezium cavity. Its sound absorption coefficients were further detected by the impedance tube detector. The actual average sound absorption coefficients for the target frequency ranges of 650–1150 Hz, 700–1200 Hz and 700–1000 Hz reached 0.8391, 0.8443 and 0.8759, respectively.
- (4)
- The consistency between the simulation data and the experimental data proved the accuracy of the acoustic finite element simulation model and the effectiveness of the joint optimization method. The revealed sound absorption mechanism by the distributions of the sound pressure at the resonance frequencies of 664 Hz, 689 Hz, 737 Hz, 791 Hz, 836 Hz, 882 Hz, 920 Hz, 962 Hz, 1011 Hz, 1080 Hz and 1140 Hz further proved the feasibility of the hexagonal acoustic metamaterial cell.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Serial Number | Symbol | Meaning |
|---|---|---|
| 1 | The total acoustic impedance of the hexagonal acoustic metamaterial cell | |
| 2 | The density of the air, 1.21 kg/m3 | |
| 3 | The acoustic velocity in air, 343 m/s | |
| 4 | The acoustic impedance of each single Helmholtz resonator | |
| 5 | The acoustic impedance of the front aperture | |
| 6 | The acoustic impedance of the rear cavity | |
| 7 | The sound angular frequency | |
| 8 | The length of aperture, 10 mm for triangular cavity and 12 mm for trapezium cavity | |
| 9 | The perforation rate | |
| 10 | The first order Bessel functions of the first kind | |
| 11 | The zero order Bessel functions of the first kind | |
| 12 | The perforation constant | |
| 13 | The dynamic viscosity coefficient of the air, 1.8 × 10−5 Pa·s | |
| 14 | The equivalent diameter of the front aperture | |
| 15 | The frequency of the incident acoustic wave | |
| 16 | The length of the rectangle aperture | |
| 17 | The width of the rectangle aperture, 5.5 mm for triangular cavity and 10.44 mm for trapezium cavity | |
| 18 | The side length of the hexagonal acoustic metamaterial cell, 50 mm | |
| 19 | The effective density | |
| 20 | The effective volumetric compressibility | |
| 21 | The thickness of the cavity | |
| 22 | The sectional area of each cavity, 423.725 mm2 | |
| 23 | The intermediate calculation coefficient | |
| 24 | The intermediate calculation coefficient | |
| 25 | The standard atmospheric pressure under normal temperature, 1.01325 × 105 Pa | |
| 26 | The specific heat rate of the air, 1.4 | |
| 27 | The intermediate calculation coefficient | |
| 28 | The thermal conductivity, 0.0258 W/(m·K) | |
| 29 | The specific heat capacity, 718 J/(kg·K) | |
| 30 | L | The length of the aperture |
| 31 | Ln (n = 1, 2, …, 6) | The length of the aperture for the six triangular cavities |
| 32 | Ln (n = 7, 8, …, 12) | The length of the aperture for the six trapezium cavities |
| 33 | C1 to C6 | The six triangular cavities |
| 34 | T1 to T6 | The six trapezium cavities |
References
- Hener, T. Noise pollution and violent crime. J. Public Econ. 2022, 215, 104748. [Google Scholar] [CrossRef]
- Karabey, T. Determining the Relationship Between Noise Sensitivity Levels and Violence Tendencies of Nursing Students. Noise Health 2023, 25, 65–69. [Google Scholar] [PubMed]
- Alimohammadi, I.; Kanrash, F.A.; Abolaghasemi, J.; Afrazandeh, H.; Rahmani, K. Effect of Chronic Noise Exposure on Aggressive Behavior of Automotive Industry Workers. Int. J. Occup. Env. Med. 2018, 9, 1375. [Google Scholar] [CrossRef] [PubMed]
- Shiue, I. Neighborhood epidemiological monitoring and adult mental health: European Quality of Life Survey, 2007–2012. Environ. Sci. Pollut. R. 2015, 22, 6095–6103. [Google Scholar] [CrossRef] [PubMed]
- Mesene, M.; Meskele, M.; Mengistu, T. The proliferation of noise pollution as an urban social problem in Wolaita Sodo city, Wolaita zone, Ethiopia. Cogent Soc. Sci. 2022, 8, 2103280. [Google Scholar] [CrossRef]
- Ma, J.; Li, C.; Kwan, M.-P.; Chai, Y. A Multilevel Analysis of Perceived Noise Pollution, Geographic Contexts and Mental Health in Beijing. Int. J. Environ. Res. Public Health 2018, 15, 1479. [Google Scholar] [CrossRef] [Green Version]
- Gao, N.; Wang, B.; Lu, K.; Hou, H. Teaching–learning–based optimization of an ultra–broadband parallel sound absorber. Appl. Acoust. 2021, 178, 107969. [Google Scholar] [CrossRef]
- Liu, X.; Yu, C.; Xin, F. Gradually perforated porous materials backed with Helmholtz resonant cavity for broadband low–frequency sound absorption. Compos. Struct. 2021, 263, 113647. [Google Scholar] [CrossRef]
- Long, H.; Liu, C.; Shao, C.; Cheng, Y.; Chen, K.; Qiu, X.; Liu, X. Subwavelength broadband sound absorber based on a composite metasurface. Sci. Rep. 2020, 10, 13823. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, L. Ultra–thin and broadband low–frequency underwater acoustic meta–absorber. Int. J. Mech. Sci. 2021, 210, 106732. [Google Scholar] [CrossRef]
- Cheng, B.Z.; Gao, N.S.; Zhang, R.H.; Hou, H. Design and experimental investigation of broadband quasi–perfect composite loaded sound absorber at low frequencies. Appl. Acoust. 2021, 178, 108026. [Google Scholar] [CrossRef]
- Gao, N.S.; Zhang, Z.C. Optimization design and experimental verification of composite absorber with broadband and high efficiency sound absorption. Appl. Acoust. 2021, 183, 108288. [Google Scholar] [CrossRef]
- Xu, J.H.; Zhu, X.F.; Chen, D.C.; Wei, Q.; Wu, D.J. Broadband low–frequency acoustic absorber based on metaporous composite. Chin. Phys. B 2022, 31, 064301. [Google Scholar] [CrossRef]
- Li, H.M.; Wu, J.W.; Yan, S.L.; Mao, Q.B. Design and study of broadband sound absorbers with partition based on micro–perforated panel and Helmholtz resonator. Appl. Acoust. 2023, 205, 109262. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, X.; Ju, Z.G.; Zhao, J.; Hu, M.; Gao, M.Y.; Luo, J.; Pu, H.Y. Ultra–Broadband Sound Absorbing Materials Based on Periodic Gradient Impedance Matching. Front. Mater. 2022, 9, 909666. [Google Scholar] [CrossRef]
- Bucciarelli, F.; Malfense Fierro, G.P.; Meo, M. A multilayer microperforated panel prototype for broadband sound absorption at low frequencies. Appl. Acoust. 2019, 146, 134–144. [Google Scholar] [CrossRef]
- Veselago, V.G.; Vinogradov, E.A.; Golovanov, V.I.; Zhukov, A.A.; Romanov, A.A.; Kapustyan, A.V.; Urlichich, Y.M.; Lavrishchev, V.P. Waveguide propagation of microwave radiation in two-layer metamaterial. Tech. Phys. Lett. 2011, 37, 220–222. [Google Scholar] [CrossRef]
- Iannace, G.; Ciaburro, G.; Trematerra, A. Metamaterials acoustic barrier. Appl. Acoust. 2021, 181, 108172. [Google Scholar] [CrossRef]
- Hunt, J.; Driscoll, T.; Mrozack, A.; Lipworth, G.; Reynolds, M.; Brady, D.; Smith, D. Metamaterial apertures for computational imaging. Science 2013, 339, 310–313. [Google Scholar] [CrossRef]
- Shitrit, N.; Yulevich, I.; Maguid, E.; Ozeri, D.; Veksler, D.; Kleiner, V.; Hasman, E. Spin-Optical Metamaterial Route to Spin-Controlled Photonics. Science 2013, 340, 724–726. [Google Scholar] [CrossRef]
- Yang, X.; Yang, F.; Shen, X.; Wang, E.; Zhang, X.; Shen, C.; Peng, W. Development of Adjustable Parallel Helmholtz Acoustic Metamaterial for Broad Low-Frequency Sound Absorption Band. Materials 2022, 15, 5938. [Google Scholar] [CrossRef]
- Xing, T.; Gai, X.L.; Zhao, J.J.; Li, X.H.; Cai, Z.N.; Guan, X.W.; Wang, F. Low frequency sound absorption of adjustable membrane–type acoustic metamaterials. Appl. Acoust. 2022, 188, 108586. [Google Scholar] [CrossRef]
- Jiang, P.T.; Jiang, T.X.; He, Q.B. Origami–based adjustable sound–absorbing metamaterial. Smart Mater. Struct. 2021, 30, 057002. [Google Scholar] [CrossRef]
- Yang, F.; Bi, S.; Shen, X.; Li, Z.; Zhang, X.; Wang, E.; Yang, X.; Peng, W.; Huang, C.; Liang, P.; et al. Adjustable Sound Absorber of Multiple Parallel-Connection Helmholtz Resonators with Tunable Apertures Prepared by Low-Force Stereolithography of Photopolymer Resin. Polymers 2022, 14, 5434. [Google Scholar] [CrossRef]
- Xu, Z.X.; Meng, H.Y.; Chen, A.; Yang, J.; Liang, B.; Cheng, J.C. Tunable low–frequency and broadband acoustic metamaterial absorber. J. Appl. Phys. 2021, 129, 094502. [Google Scholar] [CrossRef]
- Zhai, S.L.; Wang, Y.B.; Zhao, X.P. A kind of tunable acoustic metamaterial for low frequency absorption. Acta Phys. Sin. 2019, 68, 034301. [Google Scholar] [CrossRef]
- Duan, H.; Yang, F.; Shen, X.; Yin, Q.; Wang, E.; Zhang, X.; Yang, X.; Shen, C.; Peng, W. Acoustic Metamaterials for Low-Frequency Noise Reduction Based on Parallel Connection of Multiple Spiral Chambers. Materials 2022, 15, 3882. [Google Scholar] [CrossRef]
- Langfeldt, F.; Khatokar, A.J.; Gleine, W. Plate-type acoustic metamaterials with integrated Helmholtz resonators. Appl. Acoust. 2022, 199, 109019. [Google Scholar] [CrossRef]
- Yang, M.; Sheng, P. Sound absorption structures: From porous media to acoustic metamaterials. Annu. Rev. Mater. Res. 2017, 47, 83–114. [Google Scholar] [CrossRef]
- Tang, Y.; Xin, F.; Lu, T.J. Sound absorption of micro-perforated sandwich panel with honeycomb-corrugation hybrid core at high temperatures. Compos. Struct. 2019, 226, 111285. [Google Scholar] [CrossRef]
- Wang, E.; Yang, F.; Shen, X.; Duan, H.; Zhang, X.; Yin, Q.; Peng, W.; Yang, X.; Yang, L. Development and Optimization of Broadband Acoustic Metamaterial Absorber Based on Parallel–Connection Square Helmholtz Resonators. Materials 2022, 15, 3417. [Google Scholar] [CrossRef]
- Mahesh, K.; Kumar Ranjith, S.; Mini, R.S. Inverse design of a Helmholtz resonator based low-frequency acoustic absorber using deep neural network. J. Appl. Phys. 2021, 129, 174901. [Google Scholar] [CrossRef]
- Gai, X.L.; Xing, T.; Li, X.H.; Zhang, B.; Wang, W.J. Sound absorption of microperforated panel mounted with helmholtz resonators. Appl. Acoust. 2016, 114, 260–265. [Google Scholar] [CrossRef]
- Bi, S.; Wang, E.; Shen, X.; Yang, F.; Zhang, X.; Yang, X.; Yin, Q.; Shen, C.; Xu, M.; Wan, J. Enhancement of sound absorption performance of Helmholtz resonators by space division and chamber grouping. Appl. Acoust. 2023, 207, 109352. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Chen, T.N.; Xin, F.X.; Zhu, J.; Ding, W. New-parallel connection of the Helmholtz resonator with embedded apertures for low-frequency broadband sound absorption. Jpn. J. Appl. Phys. 2022, 61, 077001. [Google Scholar] [CrossRef]
- Liu, X.; Liu, M.; Xin, F. Sound absorption of a perforated panel backed with perforated porous material: Energy dissipation of Helmholtz resonator cavity. Mech. Syst. Signal Process. 2023, 185, 109762. [Google Scholar] [CrossRef]
- Yang, F.; Wang, E.; Shen, X.; Zhang, X.; Yin, Q.; Wang, X.; Yang, X.; Shen, C.; Peng, W. Optimal Design of Acoustic Metamaterial of Multiple Parallel Hexagonal Helmholtz Resonators by Combination of Finite Element Simulation and Cuckoo Search Algorithm. Materials 2022, 15, 6450. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Chen, Z.; Zhang, S.Y.; Li, X.J.; Zhang, H. An acoustic metamaterial composed of multi-layer membrane-coated perforated plates for low-frequency sound insulation. Appl. Phys. Lett. 2015, 106, 131–457. [Google Scholar] [CrossRef]
- Guo, J.W.; Fang, Y.; Jiang, Z.Y.; Zhang, X. An investigation on noise attenuation by acoustic liner constructed by Helmholtz resonators with extended necks. J. Acoust. Soc. Am. 2021, 149, 70–81. [Google Scholar] [CrossRef]
- Huang, S.B.; Fang, X.S.; Wang, X.; Assouar, B.; Cheng, Q.; Li, Y. Acoustic perfect absorbers via Helmholtz resonators with embedded apertures. J. Acoust. Soc. Am. 2019, 145, 254–262. [Google Scholar] [CrossRef]
- Bi, S.; Yang, F.; Tang, S.; Shen, X.; Zhang, X.; Zhu, J.; Yang, X.; Peng, W.; Yuan, F. Effects of Aperture Shape on Absorption Property of Acoustic Metamaterial of Parallel-Connection Helmholtz Resonator. Materials 2023, 16, 1597. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.S.; Deb, S. Cuckoo search: Recent advances and applications. Neural Comput. Appl. 2014, 24, 169–174. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.B.; Yuan, Z.H.; Song, Y. An integrated cuckoo search optimizer for single and multi–objective optimization problems. PeerJ Comput. Sci. 2021, 7, e370. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Le, B. Optimization of electric distribution network configuration for power loss reduction based on enhanced binary cuckoo search algorithm. Comput. Electr. Eng. 2020, 90, 106893. [Google Scholar] [CrossRef]
- Wei, W.; Ren, S.; Chronopoulos, D.; Meng, H. Optimization of connection architectures and mass distributions for metamaterials with multiple resonators. J. Appl. Phys. 2021, 129, 165101. [Google Scholar] [CrossRef]
- Langfeldt, F.; Hoppen, H.; Gleine, W. Resonance frequencies and sound absorption of Helmholtz resonators with multiple necks. Appl. Acoust. 2019, 145, 314–319. [Google Scholar] [CrossRef]
- Duan, H.Q.; Shen, X.M.; Wang, E.S.; Yang, F.; Zhang, X.N.; Yin, Q. Acoustic multi-layer Helmholtz resonance metamaterials with multiple adjustable absorption peaks. Appl. Phys. Lett. 2021, 118, 241904. [Google Scholar] [CrossRef]
- Askari, M.; Hutchins, D.A.; Thomas, P.J.; Astolfi, L.; Watson, P.L.; Abdi, M.; Ricci, M.; Laureti, S.; Nie, L.; Freear, S.; et al. Additive manufacturing of metamaterials: A review. Addit. Manuf. 2020, 36, 101562. [Google Scholar] [CrossRef]
- Gibson; Rosen, D.; Stucker, B. Additive Manufacturing Technologies: 3D Printing, Rapid Prototyping, and Direct Digital Manufacturing, 2nd ed.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Ciaburro, G.; Parente, R.; Iannace, G.; Puyana-Romero, V. Design Optimization of Three-Layered Metamaterial Acoustic Absorbers Based on PVC Reused Membrane and Metal Washers. Sustainability 2022, 14, 4218. [Google Scholar] [CrossRef]
- Xie, S.; Li, Z.; Yan, H.; Yang, S. Ultra-Broadband Sound Absorption Performance of a Multi-Cavity Composite Structure Filled with Polyurethane. Appl. Acoust. 2022, 189, 108612. [Google Scholar] [CrossRef]
- Wang, H.; Mao, Q. Development and Investigation of Fully Ventilated Deep Subwavelength Absorbers. Symmetry 2021, 13, 1835. [Google Scholar] [CrossRef]
- ISO 10534–2:1998; Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes—Part 2: Transfer-Function Method. International Organization for Standardization: Geneva, Switzerland, 1998.
- Yang, D.; Jiang, Q.; Wu, J.; Han, Y.; Ding, B.; Niu, B.; Xie, G. Acoustic slow-wave effect metamaterial muffler for noise control of HVDC converter station. Front. Mater. 2022, 8, 804302. [Google Scholar] [CrossRef]
- Zhong, H.; Gu, Y.; Bao, B.; Wang, Q.; Wu, J. 2D underwater acoustic metamaterials incorporating a combination of particle-filled polyurethane and spiral-based local resonance mechanisms. Compos. Struct. 2019, 220, 1–10. [Google Scholar] [CrossRef]
- Yang, X.; Tang, S.; Shen, X.; Peng, W. Research on the Sound Insulation Performance of Composite Rubber Reinforced with Hollow Glass Microsphere Based on Acoustic Finite Element Simulation. Polymers 2023, 15, 611. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.; Hao, L.; Zhao, X. Two-dimensional acoustic metamaterial with negative modulus. J. Appl. Phys. 2010, 108, 074911. [Google Scholar] [CrossRef]












| L | Triangular Cavity | Trapezium Cavity | ||
|---|---|---|---|---|
| Resonance Frequency | Peak Absorption Coefficient | Resonance Frequency | Peak Absorption Coefficient | |
| 6 mm | 662 Hz | 0.9401 | – | – |
| 7 mm | 717 Hz | 0.9747 | 906 Hz | 0.9593 |
| 8 mm | 756 Hz | 0.9932 | 955 Hz | 0.9094 |
| 9 mm | 796 Hz | 0.9988 | 1004 Hz | 0.8577 |
| 10 mm | 836 Hz | 0.9982 | 1039 Hz | 0.8118 |
| 11 mm | 874 Hz | 0.9922 | 1080 Hz | 0.7509 |
| 12 mm | – | – | 1115 Hz | 0.6989 |
| 13 mm | – | – | 1151 Hz | 0.6466 |
| 14 mm | – | – | 1187 Hz | 0.6064 |
| Ln | The Initial Structure with Step Perforation Rates | Target Sound Absorption Frequency Range | |||
|---|---|---|---|---|---|
| 650–1150 Hz | 700–1200 Hz | 700–1000 Hz | |||
| Triangular cavity | L1 | 6.0 mm | 6.0 mm | 6.9 mm | 6.9 mm |
| L2 | 7.0 mm | 6.6 mm | 7.3 mm | 7.3 mm | |
| L3 | 8.0 mm | 7.6 mm | 8.2 mm | 7.9 mm | |
| L4 | 9.0 mm | 8.8 mm | 9.2 mm | 8.8 mm | |
| L5 | 10.0 mm | 9.8 mm | 10.2 mm | 9.7 mm | |
| L6 | 11.0 mm | 11.0 mm | 11.0 mm | 10.0 mm | |
| Trapezium cavity | L7 | 7.0 mm | 7.5 mm | 7.4 mm | 7.0 mm |
| L8 | 8.4 mm | 8.4 mm | 8.6 mm | 7.4 mm | |
| L9 | 9.8 mm | 9.5 mm | 9.9 mm | 8.0 mm | |
| L10 | 11.2 mm | 10.8 mm | 11.5 mm | 8.7 mm | |
| L11 | 12.6 mm | 12.0 mm | 12.8 mm | 9.1 mm | |
| L12 | 14.0 mm | 13.2 mm | 14.1 mm | 9.4 mm | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, H.; Yang, F.; Shen, X.; Yang, X.; Zhang, X.; Bi, S. Study on a Hexagonal Acoustic Metamaterial Cell of Multiple Parallel-Connection Resonators with Tunable Perforating Rate. Materials 2023, 16, 5378. https://doi.org/10.3390/ma16155378
Cheng H, Yang F, Shen X, Yang X, Zhang X, Bi S. Study on a Hexagonal Acoustic Metamaterial Cell of Multiple Parallel-Connection Resonators with Tunable Perforating Rate. Materials. 2023; 16(15):5378. https://doi.org/10.3390/ma16155378
Chicago/Turabian StyleCheng, Hongxiang, Fei Yang, Xinmin Shen, Xiaocui Yang, Xiaonan Zhang, and Shaohua Bi. 2023. "Study on a Hexagonal Acoustic Metamaterial Cell of Multiple Parallel-Connection Resonators with Tunable Perforating Rate" Materials 16, no. 15: 5378. https://doi.org/10.3390/ma16155378
APA StyleCheng, H., Yang, F., Shen, X., Yang, X., Zhang, X., & Bi, S. (2023). Study on a Hexagonal Acoustic Metamaterial Cell of Multiple Parallel-Connection Resonators with Tunable Perforating Rate. Materials, 16(15), 5378. https://doi.org/10.3390/ma16155378