In Situ Study of the Microstructural Evolution of Nickel-Based Alloy with High Proportional Twin Boundaries Obtained by High-Temperature Annealing
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Raw Materials
2.2. In Situ Tensile Test
3. Results and Discussion
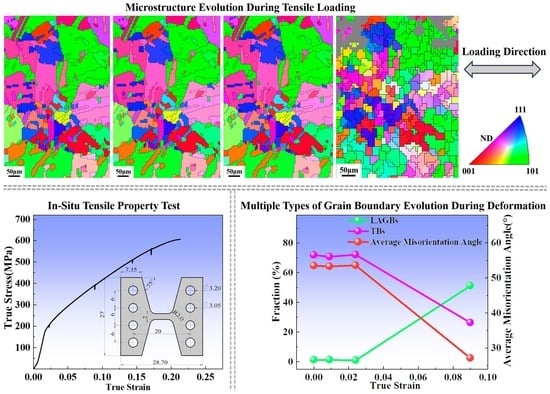
3.1. Microstructure and Mechanical Properties
3.2. Grain Orientation Distribution
3.3. Grain Boundaries Evolution
3.4. Substructure Evolution
3.5. Grain Evolution during Deformation
3.6. Schmid Factor
3.7. Texture Evolution
4. Conclusions
- During the deformation of the Cr20Ni80 alloy, the proportion of low-angle grain boundaries gradually increases, the twin boundaries tend to reduce, and the substructure gradually increases. Meanwhile, mechanical twinning is found to occur at low strain. The alloy is deformed mainly by two deformation mechanisms: dislocation slip and mechanical twinning.
- Dislocations preferentially accumulate near the twin boundary, and the strain localizes at the twin boundary with increasing strain. Meanwhile, at low strains, the geometrically necessary dislocation increases slightly with increasing strain. However, the geometrically necessary dislocation proliferates explosively under large strains, the different slip systems operate in combination, and adjacent grains interact with each other with uneven stresses, which destroys many grains. This above phenomenon can be linked to two strengthening mechanisms (dislocation strengthening and grain boundary strengthening), causing a strong work-hardening effect.
- The Copper and S orientations have low Schmid Factor values, whereas the Brass and Goss orientations have high SF values. In addition, dislocation proliferates, and interaction with dislocations and grain boundaries leads to lattice rotation, resulting in a gradual decrease in the intensity of the Brass texture and an increase in the intensity of the Copper and S texture during deformation. Meanwhile, with strain increasing, the slip system {111} <110> is activated so that dislocations start to slip along the {111} slip plane, and the grain orientation gradually rotates to a stable direction, forming the α-fiber <110>. Therefore, the grains gradually rotate toward lower Schmid Factor values during plastic deformation, eventually forming the cold deformation texture such as α-fiber (RD//<110>), R {124} <211>, S {123} <634>, and Copper {112} <111>.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, D.; Idapalapati, S.; Wei, W. Microstructural response and strain hardening in deep cold-rolled nickel-based superalloy for aerospace application. Procedia CIRP 2018, 71, 374–379. [Google Scholar] [CrossRef]
- Liao, Z.; Polyakov, M.; Diaz, O.G.; Axinte, D.; Mohanty, G.; Maeder, X.; Michler, J.; Hardy, M. Grain refinement mechanism of nickel-based superalloy by severe plastic deformation-mechanical machining case. Acta Mater. 2019, 180, 2–14. [Google Scholar] [CrossRef]
- Zhang, H.B.; Zhang, C.C.; Han, B.K.; Qiu, J.F.; Li, H.P.; Qin, S.X.; Liu, J.; Wang, Y.; Zhang, P.; Pan, Y.K.; et al. Evolution of grain boundary character distributions in a cold-deformed Nickel-based superalloy during electropulsing treatment. J. Mater. Res. Technol. 2020, 9, 5723–5734. [Google Scholar] [CrossRef]
- Thellaputta, G.R.; Chandra, P.S.; Rao, C.S.P. Machinability of Nickel Based Alloys: A Review. Mater. Today Proc. 2017, 4, 3712–3721. [Google Scholar] [CrossRef]
- Lee, H.T.; Hou, W.H. Development of fine-grained structure and the mechanical properties of nickel-based Superalloy 718. Mater. Sci. Eng. A 2012, 555, 13–20. [Google Scholar] [CrossRef]
- Nagarajan, B.; Dharmesh, K.; Fan, Z.; Castagne, S. Effect of deep cold rolling on mechanical properties and microstructure of nickel-based superalloys. Mater. Sci. Eng. A 2018, 728, 196–207. [Google Scholar] [CrossRef]
- Wojciech, P.; Adelajda, P.; Sebastian, L. Aging behavior of Haynes® 282® wrought nickel superalloy subjected to a cold pre-deformation by differential speed rolling. J. Alloys Compd. 2021, 860, 158418. [Google Scholar] [CrossRef]
- Ran, R.; Wang, Y.; Zhang, Y.X.; Fang, F.; Wang, H.S.; Yuan, G.; Wang, G.D. Microstructure, precipitates and mechanical properties of Inconel 718 alloy produced by two-stage cold rolling method. Mater. Sci. Eng. A 2020, 793, 139860. [Google Scholar] [CrossRef]
- Liu, H.L.; Zhang, M.C.; Xu, M.; Meng, Y.; Xu, G.H.; Ta, N.; Zheng, L. Microstructure evolution dependence of work-hardening characteristic in cold deformation of a difficult-to-deform nickel-based superalloy. Mater. Sci. Eng. A 2020, 800, 140280. [Google Scholar] [CrossRef]
- Xiu, X.W.; Liu, X.D.; Qi, Y.D.; Wu, W.D. Mechanical Properties and Microstructures of Ni20Cr Micro-wires with Abnormal Plastic Deformation. High Temp. Mater. Process. 2017, 36, 485–493. [Google Scholar]
- Zhou, X.W.; Qi, Y.D.; Liu, X.D. Investigation on the microstructure of as-deformed NiCr microwires using TEM. RSC Adv. 2015, 5, 90852–90857. [Google Scholar] [CrossRef]
- Bai, Q.; Zhao, Q.; Xia, S.; Wang, B.; Zhou, B.; Su, C. Evolution of grain boundary character distributions in alloy 825 tubes during high temperature annealing: Is grain boundary engineering achieved through recrystallization or grain growth? Mater. Charact. 2017, 123, 178–188. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.B.; Yang, Z.B.; Lu, S.; Harte, A.; Morana, R.; Preuss, M. Strain localisation and failure at twin-boundary complexions in nickel-based superalloys. Nat. Commun. 2020, 11, 4890. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.H.; Zhang, Y.; Zeng, Z.; Zhou, H.; He, J.; Liu, P.; Chen, M.W.; Han, J.; Srolovitz, D.J.; Teng, J.; et al. Tracking the sliding of grain boundaries at the atomic scale. Science 2022, 375, 1261–1265. [Google Scholar] [CrossRef]
- Hughes, D.A.; Hansen, N.; Bammann, D.J. Geometrically necessary boundaries, incidental dislocation boundaries and geometrically necessary dislocations. Scripta Mater. 2002, 48, 147–153. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, S.J.; Zhang, B.; Tian, X.B.; Kan, Q.H.; Kang, G.Z. Dislocation-grain boundary interaction-based discrete dislocation dynamics modeling and its application to bicrystals with different misorientations. Acta Mater. 2021, 202, 88–98. [Google Scholar] [CrossRef]
- Humphreys. Quantitative metallography by electron backscattered diffraction. J. Microsc. 1999, 195, 170–185. [Google Scholar] [CrossRef]
- Randle, V. Electron backscatter diffraction: Strategies for reliable data acquisition and processing. Mater. Charact. 2009, 60, 913–922. [Google Scholar] [CrossRef]
- Bastos, A.; Zaefferer, S.; Raabe, D.; Schuh, C. Characterization of the microstructure and texture of nanostructured electrodeposited NiCo using electron backscatter diffraction (EBSD). Acta Mater. 2006, 54, 2451–2462. [Google Scholar] [CrossRef]
- Li, W.S.; Gao, H.Y.; Nakashima, H.; Hata, S.; Tian, W.H. In-situ study of the deformation-induced rotation and transformation of retained austenite in a low-carbon steel treated by the quenching and partitioning process. Mater. Sci. Eng. A 2016, 649, 417–425. [Google Scholar] [CrossRef]
- Jia, Y.; Jiang, S.S.; Tan, J.; Lu, Z.; Jiang, J.F.; Wang, X.J. The evolution of local stress during deformation twinning in a Mg-Gd-Y-Zn alloy. Acta Mater. 2022, 222, 117452. [Google Scholar] [CrossRef]
- Zhang, C.; Ya, R.H.; Sun, M.; Ma, R.B.; Cui, J.Y.; Li, Z.P.; Tian, W.H. In-Situ EBSD study of deformation behavior of nickel-based superalloys during uniaxial tensile tests. Mater. Today Commun. 2023, 35, 105522. [Google Scholar] [CrossRef]
- Li, S.C.; Guo, C.Y.; Hao, L.L.; Kang, Y.L.; An, Y.G. In-situ EBSD study of deformation behaviour of 600 MPa grade dual phase steel during uniaxial tensile tests. Mater. Sci. Eng. A 2019, 759, 624–632. [Google Scholar] [CrossRef]
- Peng, M.D.; Shi, J.; Cui, B.; Sun, T.; Li, X.Y.; Wang, M.Q. Effect of Cold Deformation on Microstructure and Mechanical Properties of a Fe–20Mn–19Cr–0.5C–0.6N High Nitrogen Austenitic Steel. Steel Res. Int. 2017, 88, 1700069. [Google Scholar] [CrossRef]
- Niewczas, M.; Saada, G. Twinning nucleation in Cu-8 at.% Al single crystals. Philos. Mag. A 2002, 82, 167–191. [Google Scholar] [CrossRef]
- Gu, H.F.; Liu, C.Z.; Yuan, F.S.; Han, F.Z.; Zhang, Y.D.; Ali, M.; Guo, W.B.; Ren, J.; Zhang, L.F.; Wu, S.Q.; et al. Deformation twinning in octahedron-based face-centered cubic metallic structures: Localized shear-force dipoles drive atomic displacements. J. Mater. Sci. Technol. 2022, 126, 116–126. [Google Scholar] [CrossRef]
- Chen, M.W.; Ma, E.; Hemker, K.J.; Sheng, H.W.; Wang, Y.M.; Cheng, X.M. Deformation Twinning in Nanocrystalline Aluminum. Science 2003, 300, 1275–1277. [Google Scholar] [CrossRef] [Green Version]
- Christian, J.W.; Mahajan, S. Deformation twinning. Prog. Mater. Sci. 1995, 39, 1–157. [Google Scholar] [CrossRef]
- Wang, S.; Chen, J.J.; Weng, S.B. Investigation into movable dislocation evolution feature and strengthening effect for metal twin Al from atomic perspective. Acta Phys. Sin. 2022, 71, 378–386. [Google Scholar] [CrossRef]
- Li, X.; Wei, Y.; Lu, L.; Lu, K.; Gao, H. Dislocation nucleation governed softening and maximum strength in nano-twinned metals. Nature 2010, 464, 877–880. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, Q.; Kong, L.Y.; Lu, H.M.; Huang, Q.S.; Chen, Y.B.; Liu, Y.; Yang, W.; Zhang, Z.; Zhou, H.F.; Wang, J.W. Revealing extreme twin-boundary shear deformability in metallic nanocrystals. Sci. Adv. 2021, 7, eabe4758. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.F.; Wang, D.H.; He, X.L.; Wang, W.X.; Zhang, H.X.; Dong, P.; Li, C.H.; Li, Y.L.; Zhou, J.; Liu, Z.; et al. Deformation behaviors and cyclic strength assessment of AZ31B magnesium alloy based on steady ratcheting effect. Mater. Sci. Eng. A 2018, 723, 212–220. [Google Scholar] [CrossRef]
- Xu, D.D.; Thomas, E.J.; Liao, Z.R.; Maeder, X.; Ramachandramoorthy, R.; Jain, M.; Michler, J.; Axinte, D. Revealing Nanoscale deformation mechanisms caused by shear-based material removal on individual grains of a Ni-based superalloy. Acta Mater. 2021, 212, 116929. [Google Scholar] [CrossRef]
- Wei, H.; Chen, Y.L.; Zhao, Y.N.; Yu, W.; Su, L.; Tang, D. Correlation mechanism of grain orientation/microstructure and mechanical properties of Cu–Ni–Si–Co alloy. Mater. Sci. Eng. A 2021, 814, 141239. [Google Scholar] [CrossRef]
- Kuhlmann-Wilsdorf, D.; Hansen, N. Geometrically necessary, incidental and subgrain boundaries. Scr. Met. Mater. 1991, 25, 1557–1562. [Google Scholar] [CrossRef]
- Narayanswamy, S.; Saha, R.; Bhattacharjee, P.P. Cross-rolling mediated microstructure and texture evolution in severely cold-rolled and annealed ultrafine pearlite. Mater. Charact. 2021, 171, 110751. [Google Scholar] [CrossRef]
- Fan, H.D.; Wang, Q.Y.; El Awady, J.A.; Raabe, D.; Zaiser, M. Strain rate dependency of dislocation plasticity. Nat. Commun. 2021, 12, 1845. [Google Scholar] [CrossRef]
- Polkowska, A.; Lech, S.; Polkowski, W. The effect of cold rolling degree on microstructure, crystallographic texture and mechanical properties of Haynes® 282® wrought nickel superalloy. Mater. Sci. Eng. A 2020, 787, 139478. [Google Scholar] [CrossRef]
- Ji, Y.T.; Suo, H.L.; Liu, J.; Ma, L.; Liu, M.; Shaheen, K.; Wang, Y.; Zhang, Z.L.; Wang, Q.L. Effect of stress-relief annealing on rolled texture of nickel-based alloys. J. Alloys Compd. 2022, 903, 163970. [Google Scholar] [CrossRef]













Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Sun, M.; Ya, R.; Li, L.; Cui, J.; Li, Z.; Tian, W. In Situ Study of the Microstructural Evolution of Nickel-Based Alloy with High Proportional Twin Boundaries Obtained by High-Temperature Annealing. Materials 2023, 16, 2888. https://doi.org/10.3390/ma16072888
Zhang C, Sun M, Ya R, Li L, Cui J, Li Z, Tian W. In Situ Study of the Microstructural Evolution of Nickel-Based Alloy with High Proportional Twin Boundaries Obtained by High-Temperature Annealing. Materials. 2023; 16(7):2888. https://doi.org/10.3390/ma16072888
Chicago/Turabian StyleZhang, Chao, Ming Sun, Ruhan Ya, Lulu Li, Jingyi Cui, Zhipeng Li, and Wenhuai Tian. 2023. "In Situ Study of the Microstructural Evolution of Nickel-Based Alloy with High Proportional Twin Boundaries Obtained by High-Temperature Annealing" Materials 16, no. 7: 2888. https://doi.org/10.3390/ma16072888
APA StyleZhang, C., Sun, M., Ya, R., Li, L., Cui, J., Li, Z., & Tian, W. (2023). In Situ Study of the Microstructural Evolution of Nickel-Based Alloy with High Proportional Twin Boundaries Obtained by High-Temperature Annealing. Materials, 16(7), 2888. https://doi.org/10.3390/ma16072888