Figure 1.
X-observe NMR probe equipped with a z-gradient coil. (a) Photograph of the top part of the NMR probe with its metal cover removed. Added and modified components are indicated; (b) Drawing of the gradient coil support with the color plot of the calculated field gradient at the NMR sample position and the contour plot of the stray field of the gradient coil at the position of the metal tube (outer probe cover). The spatial dependence of the gradient and field values are plotted for the maximum available gradient current of .
Figure 1a displays a photograph of the gradient coil mounted on the top part of the probe. The RF coil and its thermal insulation are covered by the gradient coil and are not visible.
Figure 1b shows the drawing of the designed gradient coil support. In the inner and outer parts, the drawing contains the color coded two-dimensional plot of the gradient intensity in
z-direction
and the contour plot of the stray field
, respectively. Due to the cylindrical symmetry of the gradient coil, the field gradient and the stray field are plotted only on half space in the
-plane.
Figure 1b provides a visual impression on the calculated intensities of
and
at a gradient current of
, which corresponds to the maximum available pulsed gradient current value on our NMR systems. Details of the calculation procedure for the gradient and the stray field and the coil manufacture are given in the Experimental Section.
The analysis of the variability of the
z-gradient intensity
showed that the calculated, spatially averaged current-to-gradient conversion factor
c (
,
I gradient current) of the gradient coil is
over the anticipated sample volume. The strongest deviations from the averaged value to the higher band are observed at
, which corresponds to the inner diameter of
o.d. NMR sample tubes and, hence, does not contribute to the sensitive sample volume anymore. Thus, in agreement with the visual impression from
Figure 1b, the field gradient is expected to have sufficient homogeneity over the sample volume for NMR self-diffusion studies.
The actually achieved current-to-gradient conversion factor and the coil performance with respect to gradient linearity and eddy current depends of the individual coil manufacture. Therefore, the coil was calibrated by measuring the spin echo attenuation of liquid deuterated water (
) using
PFG NMR. For self-diffusion in liquid water, the spin echo NMR signal
is expected to follow the dependence
where
denotes NMR spin echo amplitude observed without pulsed field gradients and
D is the self-diffusion coefficient of the molecules carrying the observed nuclei. The
b-value depends on the applied pulse sequence, on the pulsed field gradient pattern
and on the gyro-magnetic ratio
γ of the observed NMR-active nucleus. It is determined via the so-called double integral (see e.g., [
6,
8,
10]). For two rectangularly shaped pulsed field gradients of duration
δ, intensity
g and separation
Δ applied in a primary or stimulated spin echo NMR sequences, one obtains
The experimental
PFG NMR spin echo attenuation curve (
over
b) of deuterated water is plotted in
Figure 2. In this semi-logarithmic presentation, the observed decay is linear, which means that the designed coil and the modified X-observe NMR probe follow the behavior expected from Equation
1. Weingärtner
et al. [
23] reported that
has a self-diffusion coefficient of
at
. This value was applied to calibrate the current-to-gradient conversion factor
c of the new probe in such a way that the slope of the
PFG NMR spin-echo attenuation curve in
Figure 2 corresponds to this known self-diffusion coefficient. The obtained conversion factor is
. This value is in agreement with the value predicted by the gradient coil simulation. It means that pulsed field gradients of up to
may be generated for the NMR diffusion studies with X-nuclei using the maximum available gradient current of
. Moreover, the experimentally achieved rise and fall times from
to maximum gradient strength are
and
, respectively. These short values are achieved by using exponentially shaped gradient wave forms as described in reference [
8]. They are significantly shorter than the nominal values for rise and fall times in commercially available
z-gradient probes of similar maximum gradient strength and are of advantage when using the system for diffusion studies of fluids with short transverse relaxation times as observed in many porous materials.
Figure 2.
Pulsed field gradient calibration and performance tests of the X-observe probe equipped with a z-gradient coil for NMR diffusion studies. NMR spin echo attenuations due to self-diffusion of , , in aqueous solutions as well as of bulk deuterated water and enriched benzene (see legend) observed using , , , , and resonance, respectively.
The performance of the modified probe at different resonance frequencies was investigated by PFG NMR measurements of self-diffusion of several monovalent cations (
,
,
) in aqueous solution and of liquid benzene using the NMR active nuclei
,
,
and
, respectively. For all these different systems, the slope in
Figure 2 is found to be linear. Using the current-to-gradient conversion factor obtained by the
PFG NMR measurements, the self-diffusion coefficients were determined. The values are given in
Table 1. Within the experimental uncertainty, they agree well with data known for these systems from literature. It shall be noted that—due to the relatively small self-diffusion coefficient of
in this aqueous solution and the short observation time of
—it was necessary to apply the maximum pulsed gradient intensity of
to attenuate the
NMR spin echo signal amplitude by one order of magnitude as shown in
Figure 2. Thus, the positively measured root mean square (r.m.s.) displacements of the
cations in this system are
.
2.1.1. Diffusion of and Cations in Mesocellular Silica Foam
Besides the performance test of the modified X-observe NMR probe, the results for
and
self-diffusion in bulk aqueous solution presented in
Table 1 serve as reference for comparison with the diffusion behavior of these cations in a mesoporous silica foam (MCF). The successful impregnation of the MCFs by the electrolyte solutions was checked prior to the NMR diffusion studies by visual inspection of the sample texture. Although more than approximately 200-weight% of solution were added to the MCF powder, the individual particles in the bed do not adhere due to capillary forces between outer solid and liquid interfaces. Thus, the presence of significant amounts of external (excess) liquid between the MCF particles can be excluded.
Table 1.
Diffusion coefficients of monovalent cations in aqueous solutions in bulk and captured in mesocellular silica foam (MCF) as measured by the modified X-observe NMR probe. The data are compared to literature values known for bulk solutions [
24]. The
data from Weingärtner
et al. [
23] were used to experimentally calibrate the current-to-gradient conversion factor of the modified probe.
Table 1.
Diffusion coefficients of monovalent cations in aqueous solutions in bulk and captured in mesocellular silica foam (MCF) as measured by the modified X-observe NMR probe. The data are compared to literature values known for bulk solutions [24]. The data from Weingärtner et al. [23] were used to experimentally calibrate the current-to-gradient conversion factor of the modified probe.
| Observed X-nucleus and substance | | τ | | Reference |
|---|
| in (bulk) | | – | | [24] |
| in (MCF) | | | – | – |
| in (bulk) | | – | | [24] |
| in (bulk) | | – | | [24] |
| in (MCF) | | | – | – |
| (bulk) – calibration | | – | | [23] |
Due to the high porosity (high specific pore volume of ) of the MCF and the relatively high concentration of the aqueous solutions (about 75% and 85% of the respective saturation concentration at room temperature), the signal-to-noise ratio of the and the primary spin echo NMR signal is better than for a single scan. The total amounts of and spins in the impregnated MCF samples were and , respectively. By using signal averaging to further improve the signal-to-noise ratio, it is estimated that the modified X-observe probe will be well suited to investigate diffusion of these monovalent cations in aqueous solutions in a concentration range down to about of the values used in these experiments. Thus, concentrations of a few percent of the saturation concentration at room temperature are accessible for NMR diffusion studies of these cations in such porous materials.
Due to the good signal-to-noise ratio, spin echo attenuations over more than one order of magnitude were readily measured in the
and
PFG NMR experiments with the electrolyte impregnated MCFs. The
NMR data showed a single-exponential decay and were straightforwardly analyzed by using Equation (
1). The obtained
self-diffusion coefficient in the MCF is given in
Table 1. It is reduced by a factor (
τ) of about
compared to the value in the bulk solution. This is due to the restricting influence of the MCF matrix on the Brownian motion of the cations in the solution.
In the corresponding
NMR measurements, small contributions from fast bulk cation diffusion were found. Obviously, due to the increased viscosity of the
solution, not all of the solution added to the MCF was sucked into the pore space of the silica foam. These contributions were subtracted from the spin echo attenuation before determining the
cation diffusion coefficient in the MCF. The result is given in
Table 1. With
it is again more than a factor of 4 smaller than the
cation diffusion in the bulk aqueous
solution.
It shall be noted that the cation self-diffusion coefficient in the MCF is the smallest self-diffusion coefficient determined with the modified X-observe probe within this paper. The observation time for this measurement was corresponding to a r.m.s. displacement of in pulsed field gradient direction. This value provides an upper estimate of the displacements, which can positively be measured by the modified X-observe NMR probe.
This displacement is large compared to the pore size but smaller than the particle size of the MCF. Thus, the cations can easily move within the particles. They just experience an averaged obstruction due to the presence of the solid matrix during traveling between the individual pores. If compared to the bulk cation diffusion, the impact of this obstruction is the same for the
and the
cations (see
Table 1). The ratio of the two diffusivities
represents the tortuosity
τ of the pore space. As a geometrical pore structure parameter,
τ describes the square of the averaged increase of fluid path way through the pore space
L compared to the direct (straight line) connection
, see second part of Equation
3. A tortuosity of about
for the MCF is reasonable and means that the cations have to increase their diffusion path through the silica foam by slightly more than a factor of two in order to reach the same displacement as in the bulk solution.
2.1.2. Diffusion of and in MOF CuBTC
In the microporous crystalline metal-organic framework CuBTC, the adsorption capacities for
at room temperature and ambient pressure (
) are in the range of
[
25]. Since the NMR sample tube contains about
of the adsorbent in a bed of
filling height, there are up to about
in the sensitive NMR volume. Thus, the typical number of NMR active nuclei for the
NMR studies with the adsorbed
-enriched
is slightly smaller than the number of
and
nuclei in the aqueous salt solutions, described above.
The modified X-observe probe is capable to observe the
NMR signal of the adsorbed
quantitatively.
Figure 3 displays the NMR signal intensity, observed with a CPMG sequence [
26] of all mixture samples (samples M1–M5 in
Table 2) as function of the amount of
loaded onto the NMR sample tubes during sample preparation. The plotted signal intensities were obtained by mono-exponential fits of the measured spin echo intensities in the CPMG echo trains. The signal intensities increase monotonously with these
amounts, but there is some scatter in the data. Since the NMR signal intensity is proportional to the amount of NMR active nuclei and since the observed NMR signal intensities are found to be reproducibly measured, we recalculated the loading of the samples from the NMR signal intensities. The results are given in
Table 2. A similar procedure was applied for the methane loadings which were checked by
NMR using our standard diffusion probe described in [
8]. All loadings and the adsorbed
molar fraction in
Table 2 refer to this corrected values. Deviations from the introduced amounts of the adsorbed gases are caused by incomplete transfer of the volumetrically determined amounts of gases to the NMR sample tubes and scatter in the void volume of the sample tubes above the CuBTC bed, which is filled by gas in equilibrium to the corresponding adsorbed amounts.
Figure 3.
NMR signal intensity observed with a CPMG sequence in dependence on the volumetrically determined amounts of
chilled onto the CuBTC mixture samples M1 to M5. The solid line represents the best fit to the data and was used to determine the amount of adsorbed
from the
NMR signal intensities (see
Table 2).
Figure 3.
NMR signal intensity observed with a CPMG sequence in dependence on the volumetrically determined amounts of
chilled onto the CuBTC mixture samples M1 to M5. The solid line represents the best fit to the data and was used to determine the amount of adsorbed
from the
NMR signal intensities (see
Table 2).
Our own earlier
NMR studies of
to
alkanes in MOF CuBTC showed that the longitudinal (
) relaxation times of the adsorbed molecules at room temperature are rather short, which limits NMR diffusion studies to short observation times of
using the primary spin echo sequence [
27]. Dipole-dipole interactions with the electron spin of framework and extra framework
in the CuBTC structure and the reduced molecular mobility were identified as reasons for fast relaxation.
Figure 4 shows the
and
longitudinal relaxation rates (
) of
and
in the mixture samples. The relaxation rates for
are independent of loading and significantly smaller than for
. The
relaxation times are
and sufficiently long to apply stimulated spin echo based PFG NMR sequences. The
relaxation rates of methane seem to increase for large carbon dioxide contents, which correspond to large total loadings but small methane contents (see
Table 2). We assume that this indicates a reduced mobility of methane due to the presence of a large amount of carbon dioxide in the pore space. The
relaxation times of methane are in the range of
to
, which again limits the applicability of observation time dependent NMR diffusion studies and requires the use of high pulsed field gradient intensities as already known for the longer alkanes [
27].
Figure 4.
and
longitudinal relaxation rates (
) in CuBTC for adsorbed
(▲) and
(□), respectively. The data are plotted for the mixture samples M1 to M5 in dependence on the amount of adsorbed
(see
Table 2).
Figure 4.
and
longitudinal relaxation rates (
) in CuBTC for adsorbed
(▲) and
(□), respectively. The data are plotted for the mixture samples M1 to M5 in dependence on the amount of adsorbed
(see
Table 2).
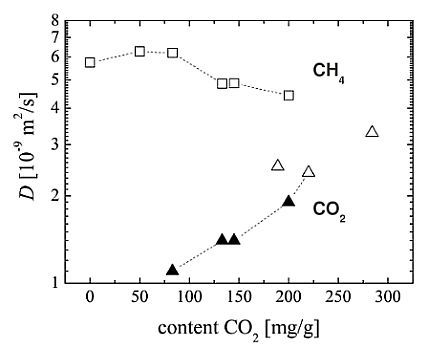
The self-diffusion coefficients of carbon dioxide and methane in CuBTC determined by
and
PFG NMR, respectively, are shown in
Figure 5. In all samples, diffusional exchange of the adsorbed phase with the faster diffusing gas phase between the CuBTC crystallites in the bed was observed. The data reported in
Figure 5 represent the intracrystalline self-diffusion coefficients, which were obtained from the PFG NMR spin echo attenuations by application of a bi-exponential analog of Equation
1 and assigning the smaller diffusivity to the diffusion of the adsorbed phase.
Single-component
diffusivites were measured over a narrow range of loadings and yield self-diffusion coefficients of about
with a tendency to increase with loading. According to our knowledge, there are no published data for single-component
self-diffusion in CuBTC available. However, results from MD simulations and experimental studies in other MOF systems (IRMOF, MIL, ZIF) show that carbon dioxide is generally highly mobile in these structures and should show an increasing diffusivity with increasing loading, as long as no clustering of
molecules in the pore space will occur [
4,
28,
29,
30].
For CuBTC, MD simulation predicts for single-component self-diffusion of methane a value of
at room temperature [
27]. With
(see
Figure 5 at the zero
content) our experimental result is about a factor of three smaller. Possible reasons are a different loading range (higher loading in the experimental study) and a restricting influence of the external crystal surface of the CuBTC MOF on the methane diffusion. Due to the small
relaxation times of the methane in CuBTC (see
Figure 4), this restricting influence could not be evaluated quantitatively by changing the observation time over a sufficiently large interval in the
PFG NMR experiments.
For the experimental
and
PFG NMR diffusion with co-adsorbed carbon dioxide and methane the samples were prepared under such conditions that the total pressure in the gas phase above the CuBTC bed is not exceeding but close to
. In
Figure 5, the corresponding data points including the single-component results for zero and
content are connected with a dashed line. With increasing
content, the diffusivity of carbon dioxide in the mixture increases resuming the trend observed for the single-component
data. The self-diffusion coefficients for the co-adsorbed methane, which always diffuses faster than the
in the considered range of loadings, are found to decreases slightly.
Figure 5.
Self-diffusion coefficients
D in MOF CuBTC in dependence on the adsorbed amount of
:
(▲) and
(□) for the co-adsorption of both gases;
(△) under single component adsorption. The corresponding methane loadings and total loadings in molecules per u.c. are given in
Table 2.
Figure 5.
Self-diffusion coefficients
D in MOF CuBTC in dependence on the adsorbed amount of
:
(▲) and
(□) for the co-adsorption of both gases;
(△) under single component adsorption. The corresponding methane loadings and total loadings in molecules per u.c. are given in
Table 2.
From experimental studies and computer simulation it is known that carbon dioxide is more strongly adsorbed in CuBTC than methane [
13,
25,
31,
32]. At small carbon dioxide contents, most of the carbon dioxide is attracted to strong adsorption sites. The co-adsorbed methane cannot compete in host-guest interaction. Thus, methane diffusion in the potential of the MOF framework is faster than carbon dioxide diffusion. With increasing carbon dioxide loading, the averaged interaction with the host lattice becomes smaller since the strongest adsorption sites are already covered and the carbon dioxide diffusion increases. This behavior is in agreement with such pattern of loading dependent diffusivities in microporous materials, where increasing amounts of molecules strongly interacting with the host system reduce the potential barrier on the diffusion path through the pore space or the life time in the transition state [
3].
With increasing carbon dioxide content (which corresponds to a decreasing methane content), the diffusion path of methane in the pore space is influenced by the presence of more and more molecules occupying the pore space. The majority of these molecules is slowly diffusing . Thus the free volume for methane is continuously reduced, leading to the observed slightly decreasing methane diffusion coefficients.
The ratio between the methane and the carbon dioxide diffusivities, which is called the diffusion separation factor (
), is important for estimating the performance of microporous materials in gas separation processes.
Figure 5 and
Table 2 show that this ratio depends mainly on the adsorbed carbon dioxide content. It decreases from about
at an adsorbed carbon dioxide molar fraction of
to
at
. Using only the experimental single-component self-diffusion coefficients one obtains also a value of about
.
Several computer simulations of the performance of CuBTC in
gas separation applications report on separation factors [
22,
33]. For methane and carbon dioxide, Keskin
et al. [
34] investigated also diffusion separation factors, without reporting the corresponding single-component self-diffusion coefficients in the mixture. In this mixture MD simulation study, where the molar ratio of both gases in the gas phase is
, a cross-over from
at pressures
to smaller than unity is observed at a total pressure of about
[
34] (corresponding to
partial pressure). The cross-over in the ratios of the self-diffusion coefficients means that the
is expected to diffuse faster at high total loadings than the
.
Our experimental results for
at
agree with these MD predictions (see
Table 2). Extrapolating our NMR data in
Figure 5 towards higher carbon dioxide contents, we expect the cross-over at a carbon dioxide loading of about
. Using the adsorption isotherm published by Martin-Calvo
et al. [
33], the corresponding partial
pressure in the gas phase is estimated to be about3–
. Thus, our observed dependence of the self-diffusion coefficients on adsorbed
content confirms the cross-over of the diffusion separation factor predicted by the mixture MD simulations as well. It will be an interesting challenge for future experimental PFG NMR studies with the modified X-observe probe to explore directly the diffusion of
containing gas mixtures in MOFs and other microporous materials in the high-pressure range.