Bismuth Telluride and Its Alloys as Materials for Thermoelectric Generation
Abstract
: Bismuth telluride and its alloys are widely used as materials for thermoelectric refrigeration. They are also the best materials for use in thermoelectric generators when the temperature of the heat source is moderate. The dimensionless figure of merit, ZT, usually rises with temperature, as long as there is only one type of charge carrier. Eventually, though, minority carrier conduction becomes significant and ZT decreases above a certain temperature. There is also the possibility of chemical decomposition due to the vaporization of tellurium. Here we discuss the likely temperature dependence of the thermoelectric parameters and the means by which the composition may be optimized for applications above room temperature. The results of these theoretical predictions are compared with the observed properties of bismuth telluride-based thermoelements at elevated temperatures. Compositional changes are suggested for materials that are destined for generator modules.1. Introduction
Since the observation [1], sixty years ago, of a substantial lowering of temperature by means of the Peltier effect in a thermocouple incorporating bismuth telluride, Bi2Te3, this compound has been extensively used in the construction of thermoelectric modules. The performance of these modules has steadily improved, since the original observations, due to a number of factors. The thermoelectric figure of merit [2], which nowadays usually appears in its dimensionless form, ZT, has increased from the order of 0.5 to values significantly greater than one. Here Z is defined as α2σ/λ, where α is the Seebeck coefficient, σ is the electrical conductivity and λ is the thermal conductivity. Strictly speaking, Z should be defined for a pair of thermoelements, since the Peltier and Seebeck effects are manifest for thermocouples rather than single materials, but it is convenient to select materials on the basis of the maximization of Z for each branch. It is only when the two branches have widely different properties that this strategy must be modified as, for example, when one branch is a superconductor [3,4].
From the outset it was realized that there was the need to optimize [1,2] the charge carrier concentration, by doping with donor or acceptor impurities. When there is only one type of carrier, electrons or positive holes, the Seebeck coefficient at a given temperature falls as the electrical conductivity increases. The Seebeck coefficient and the electrical conductivity are combined in a quantity, α2σ, known as the power factor. One aims to make this parameter as large as possible, though it must be remembered that a large electrical conductivity also implies a large electronic component of the thermal conductivity. Most of the early improvements came about through a reduction in the lattice component of the thermal conductivity, λL. This was achieved through the use of solid solutions [5] of bismuth telluride with the isomorphous compounds antimony telluride and bismuth selenide. The enhanced scattering of phonons in these solid solutions is not usually accompanied by a reduction in the mobility of the charge carriers. This is somewhat surprising since the charge carriers usually possess the larger mean free path.
In recent years, further reductions in the lattice conductivity have been obtained by the adoption of nanostructures. Although the original aim seems to have been the improvement of the power factor through quantum confinement effects [6], in actual fact it appears that the main advantage has stemmed from phonon scattering on the boundaries of nano-sized grains [7,8]. In other words, nano-structuring usually seems to affect the lattice conductivity rather than the electronic transport properties.
It is important to realize that the same figure of merit applies for thermoelectric generation [2], using the Seebeck effect, as for refrigeration using the Peltier effect. Thus, at any given temperature, the best refrigeration material will also be the best material for generation. In so far as bismuth telluride alloys are the best materials at room temperature, they must also be the best generator materials, at least close to this temperature.
One must remember that the electrical and thermal conductivities of bismuth telluride are anisotropic [9] although the Seebeck coefficient does not depend on orientation in the extrinsic or one-carrier regime. The lattice conductivity is about twice as large along the cleavage planes as it is in the perpendicular direction [10]. The anisotropy of the hole mobility is almost the same as that of the lattice conductivity so that, although the electrical and thermal conductivities in aligned crystals are different from those in randomly oriented polycrystalline material, the figure of merit is virtually isotropic for p-type bismuth telluride. On the other hand, the electron mobility is more strongly anisotropic than the lattice conductivity and this means that the figure of merit is significantly less for non-aligned n-type samples [11] than it is for properly oriented material. This is unfortunate since there are practical advantages in making material in polycrystalline form using a sintering process rather than a melt-growth process. For example, the concept of a bulk nanostructure is probably most easily realized using sintered material. Unless some measure of orientation can be achieved during sintering, the advantage of a reduction in the lattice conductivity due to nanostructuring may be outweighed by a fall in the power factor, α2σ.
2. Effect of Temperature on the Thermoelectric Properties
2.1. Single Carrier Conduction
Let us first discuss the behavior of a material with a single parabolic conduction or valence band. At any particular temperature there will be an optimum value of the Fermi energy, EF, and a corresponding optimum Seebeck coefficient. This will be determined predominantly by the need to maximize the power factor, but there will also be some influence from the electronic component, λe, of the thermal conductivity, unless this quantity is negligibly small compared with the lattice component, λL.
When the temperature is raised while the carrier concentration stays constant, the Fermi energy moves out of the band and into the energy gap [12]. The Seebeck coefficient eventually rises above its optimum value, a value that is more-or-less independent of temperature. Material intended for use at higher temperatures should have an increased carrier concentration to match the temperature- dependent Seebeck coefficient to the range of operation. This means that the dimensionless Fermi energy η, equal to EF/kT, will remain almost independent of temperature. Since the effective density of states 2(2πm*kT/h2)3/2 is proportional to T3/2, the carrier concentration for a fixed value of η is also proportional to T3/2. Also, if the carriers are scattered by acoustic-mode phonons, the mobility should vary as T−3/2. Thus, the optimum electrical conductivity for this simple model should not vary with temperature. This means that the optimum power factor α2σ should also be temperature independent. We note that α2σ/λe will decrease as the temperature rises, since λe is proportional to T, in so far as the Wiedemann-Franz law is applicable. However, ZT is equal to α2σT/(λe + λL) where λL is usually appreciably larger than λe. Moreover, λL generally decreases with increasing temperature (the variation will vary from T−1 for a pure element or compound to T0 when alloy scattering is completely dominant [13]). Thus, the total thermal conductivity may be approximately independent of temperature since the temperature variations of the two components may just about balance out.
Let us consider a hypothetical optimized material that happens to have ZT equal to 1. We may write an approximate expression for ZT in terms of the ratio C of the lattice conductivity to the electronic thermal conductivity. The optimum Seebeck coefficient will be close to 2.5 (k/e) (i.e., 216 μV/K). We suppose that the electronic thermal conductivity is equal to A(k/e)2σT, where A is equal to about 2 for a conductor that is not strongly degenerate and for which acoustic-mode lattice scattering is predominant. The expression for ZT is then:
Thus, if ZT is equal to about 1, C is equal to about 2.1. This means that in a typical optimized thermoelectric material the lattice conductivity is just over twice the electronic thermal conductivity.
In Figure 1 we plot the total thermal conductivity, relative to the electronic thermal conductivity at 300 K, against temperature, for the two extremes of the lattice conductivity, i.e., λL proportional to T−1 and T0. The electronic thermal conductivity has been calculated using Fermi-Dirac statistics [12]. It will be seen that the assumption that the thermal conductivity is more-or-less independent of temperature is likely to be a good approximation. Our overall expectation, then, is that ZT at the optimum Seebeck coefficient should rise with increasing temperature, perhaps being approximately proportional to T.
Our model is not quite valid for bismuth telluride and its alloys, even when the temperature is low enough for there to be only one type of charge carrier [14]. The carrier mobility in the non-degenerate region has been assumed to be proportional to T−3/2 whereas it is actually observed to vary as T−1.72 and T−1.94 for n-type and p-type material respectively. Likewise, the plot of Seebeck coefficient against lnT should be approximately linear with a slope of 3k/2e or 129 μV/K whereas the actual slope is somewhat greater, for example 150 μV/K for n-type samples. However, when it comes to calculating the temperature variation of the power factor α2σ, for a given reduced Fermi energy, these deviations from the simple theory approximately cancel one another. This is evident from the data given in Table 1.
In Table 1 the electrical conductivities at 150 K and 300 K of n-type and p-type bismuth telluride are given for constant values of the Seebeck coefficient. The ratios of the conductivities at the two widely different temperatures are close to unity. It is, therefore, a good approximation to state that the electrical conductivity for a given Seebeck coefficient is independent of the temperature. Our prediction that ZT should be approximately proportional to T should hold for bismuth telluride alloys provided that there is only one type of charge carrier.
2.2. Region of Mixed Conduction
It is a different matter when we enter the temperature range for which minority carriers have to be considered. The energy gap [15,16] of the compound Bi2Te3 at 300 K is only about 5kT, which means that, for typical samples, minority carriers are not entirely negligible.
Minority carriers are undesirable for two reasons. Since they have thermoelectric coefficients that are opposite in sign to those of the majority carriers, they reduce the overall Seebeck coefficient. Also, they can make a large contribution to the thermal conductivity through the bipolar effect [4].
Provided that the energy gap is not too small, the harmful minority carrier effects can be minimized by increasing the concentration of the majority carriers. This reduces the Seebeck coefficient but the increase in electrical conductivity almost makes up for this when the power factor is calculated. Increasing the doping level is clearly one way of minimizing the minority carrier effects in bismuth telluride. However, one must also take into account an increase in the single-carrier electronic thermal conductivity as the carrier concentration rises.
The maximum value of the Seebeck coefficient for a non-degenerate semiconductor is simply related to the energy gap, Eg. In general, it is a good approximation [17,18] to set αmax equal to ±Eg/2eT unless there is a very large ratio between the electron and hole mobilities. Thus, if bismuth telluride has an energy gap equal to 5kT, the maximum Seebeck coefficient is estimated to be about ±5k/2e, or ±216 μV/K. In actual fact, the Seebeck coefficient of this compound can exceed ±250 μV/K but it is not surprising that the estimate is rather crude in view of the partial degeneracy that must exist. The fact that the maximum Seebeck coefficient is so close to the optimum value for a single band indicates that minority carrier conduction is already having some influence at room temperature. There is absolutely no doubt that minority carrier conduction must be taken into account for bismuth telluride thermoelements that are designed for use at higher temperatures. This means that we must accept lower values of the Seebeck coefficient, perhaps less than ±200 μV/K, for operation at upwards of, say, 400 K.
Of course, the most obvious way of extending the effectiveness of bismuth telluride alloys to higher temperatures is by increasing the energy gap. It is likely that the energy gap in a solid solution will be different from that of either of its components. For narrow-gap semiconductors the Kane [19] model suggests that the inertial effective mass will rise with increasing gap leading to a decrease in the mobility. We might think, then, that there could be a general rule that the larger the energy gap the smaller the carrier mobility and also, perhaps, μ(m*/m)3/2, where m* is the density-of-states mass. However, we have not been able to establish a clear relationship between either μ or μ(m*/m)3/2 and the energy gap for all those semiconductors for which data were available [20]. There is some indication that the mobility falls with increasing gap but the trend is not very clear. This is somewhat surprising but it does not alter the fact that the best thermoelectric materials at any given temperature often have values of the energy gap that are no more than a few kT.
There is the possibility that some of the solid solutions may have larger energy gaps than bismuth telluride itself. The variation of energy gap with composition has been studied for the Bi2Te3-Bi2Se3 system by Greenaway and Harbeke [16]. As shown in Figure 2, it appears that the energy gap rises by a factor of about 2 as x changes from 0 to 1 in the series Bi2Te3−xSex. It seems [21] that the largest gap occurs when x = 1. This should allow minority carrier conduction to be all but eliminated up to a temperature of about 500 K. However, the electron mobility becomes smaller as Se is added and it is usual to restrict the value of x to no more than 0.45 in n-type thermoelements for refrigeration modules [22]. Bismuth seleno-telluride alloys are commonly used as the negative components in such modules, probably because the required concentration of donor impurities to optimize the carrier concentration is less than it would be for pure bismuth telluride or for alloys containing antimony. There has been little work done on the use of bismuth seleno-telluride alloys as p-type materials, probably because it is easier to optimize p-type bismuth-antimony telluride.
There is little evidence that the energy gap changes significantly as antimony telluride is added to bismuth telluride though, until recently, it was thought that solid solutions containing more than about 75% of Sb2Te3 must have a smaller gap width since it has been a challenge to obtain a Seebeck coefficient of even 200 μV/K for such materials. It is unusual to find a Seebeck coefficient above 150 μV/K for Sb2Te3 itself, and this could indicate that the energy gap is smaller than that of Bi2Te3. However, it now appears that this is due to the non-stoichiometry in this compound rather than a small energy gap [23]. It is difficult to add enough donor impurity to compensate for the large inbuilt acceptor concentration. Sun et al. [24] have shown that the Seebeck coefficient can rise to about 200 μV/K at 500 K even when it is no more than about 175 μV/K at room temperature. This suggests that the energy gap is at least as large as that of Bi2Te3. ZT is rather small, being only about 0.25 at room temperature, but it was found to rise to about 0.55 at 550 K. The thermal conductivity is not particularly high, so the low figure of merit is due to a rather small power factor (the electrical conductivity is much smaller than that of bismuth telluride with the same Seebeck coefficient). It is apparent from this work that alloys that are rich in Sb2Te3 may be useful generator materials. Mehta et al. [25] think that the energy gap of Sb2Te3 may well be greater than that of Bi2Te3. They suppressed the anti-site defects that normally exist in Sb2Te3 by doping with sulfur. As a result they were able to obtain ZT equal to 0.95 at 420 K.
One of the developments in recent years has been the introduction of energy filtering as a means of controlling the Seebeck coefficient. For example, it is possible [26] to improve the power factor in PbTe by doping with Tl. In this case, the energy states associated with Tl are located well inside the main energy band, and this leads to an enhanced Seebeck coefficient. It is possible that a similar effect occurs when Sn is added to bismuth telluride [27]. This may allow the Seebeck coefficient to remain high when the Fermi energy lies deep within the main band, thus minimizing the minority carrier contribution.
Another possibility, that would allow a higher Seebeck coefficient to be achieved with a narrow gap, is the introduction of ionized-impurity scattering. Ioffe [2] showed that the increase in the energy transported by the charge carriers, following the introduction of ionized-impurity scattering, could more than compensate for the reduction in the electrical conductivity in the determination of the power factor. However, the effect predicted by Ioffe would require rather precise control of the proportion of the scattering due to the impurities, and it would be of only marginal benefit in an extrinsic material. On the other hand, the effect would be much more beneficial in a mixed or near-intrinsic conductor [28]. It has been shown that the maximum Seebeck coefficient in a bismuth-like zero-gap conductor could be increased from 104 μV/K with lattice scattering to 242 μV/K with the optimized proportion of ionized-impurity scattering. Presumably, one could increase the contribution of ionized-impurity scattering by counter-doping, though it must be admitted that such scattering is not usually observed in bismuth telluride. That is because such a material has a very large dielectric constant, which shields the carriers from the coulombic field of the impurity ions.
3. Experimental Observations
In 1982, Goldsmid and Cochrane [29] designed a thermoelectric generator to work from a solar collector with a non-tracking concentrator. Their design made use of bismuth telluride alloys with a maximum operating temperature of 200 °C. They showed clearly that ZT at high temperatures could definitely be increased by raising the carrier concentration even though such heavily doped material would not be much good for refrigeration. After optimization, there was little change of ZT with temperature over the range 300 K to 450 K. The maximum value of ZT at 300 K for a p-type alloy was less than unity and could certainly be improved using nano-structuring. Nevertheless it is still probably true that the optimum Seebeck coefficient at different temperatures is likely to be little changed for a nanostructure. Goldsmid and Cochrane found that the best material for use at 200 °C should have a Seebeck coefficient of less than 150 μV/K at 300 K, and the virtue of choosing such a material is evident when we make a comparison with, say, the data of Imaduddin and Dupre [30] who studied p-type alloys in the temperature range 300 K to 600 K.
The thermoelectric properties of the alloys of bismuth telluride have been reviewed by several authors over the past few decades. One of the most comprehensive treatments is that of Scherrer and Scherrer [31,32]. It is generally accepted that these alloys are the best available materials for generation as well as refrigeration near room temperature [33]. Even when higher temperature sources are available, bismuth telluride alloys should be used at the low temperature ends of segmented thermoelements.
Although the problem of improving the composition of bismuth telluride alloys for low temperature applications has been treated successfully by Kutasov et al. [34], there seems to have been little attempt to optimize these materials for use at high temperatures.
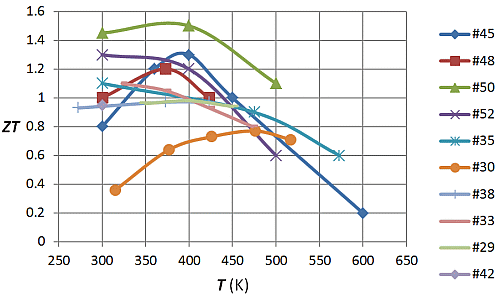
Son et al. [35] produced a p-type bismuth telluride alloy using a sintering process. They found that they could control the grain size by adjustment of the ball milling time during the preparation of the powders. The grain size was small enough for the material to be described as a bulk nanostructure. An interesting feature of their observations is the clear demonstration of the need to optimize the doping for high temperature material. For example, the material with the highest value of ZT of 1.1 at 300 K had the rather low value of about 0.2 at 575 K. On the other hand, a sample with ZT equal to 0.5 at 300 K had a value of 0.6 at 575 K with a maximum of 0.9 at about 475 K.
The problem of optimizing the impurity content of bismuth telluride alloys for specific temperatures has been tackled by Kuznetsov [36] in the production of functionally graded thermoelements. Min and Rowe [37] discussed the optimization of Peltier modules for use in power generation but did not treat the question of the composition of the thermoelements. Matsuura and Rowe [38] selected bismuth telluride alloys as the preferred generator materials up to 150 °C but did not consider the optimization of the Seebeck coefficient. It is noteworthy, however, that their n-type alloy, Bi2Te2.25Se0.75, displayed an almost constant value of 2 × 10−3 K−1 for Z at all temperatures from 0 °C to 150 °C, which implies a continuous rise of ZT with temperature over this range. Dashevsky et al. [39] reviewed generator materials up to 800 °C, specifying Bi2Se0.6Te2.4 and Bi0.5Sb1.5Te3, as the n-type and p-type materials up to 300 °C, but without discussing the optimization of the carrier concentration.
Kusano and Hori [40] described the properties of Bi0.4Sb1.6Te3 with 0.3 wt% of PbTe and showed that ZT rose from about 1.0 at 323 K to 1.1 at 380 K and then fell to 0.8 at 623 K. The material was produced by spark plasma sintering and, presumably, did not display any nanostructure effects. It may well represent the best that can be done without nanostructuring unless the energy gap can be increased to minimize the effect of minority carrier conduction.
It has generally been found that good n-type bismuth telluride alloys are more difficult to produce than their p-type counterparts. This is in part due to the rather high ratio of the electron mobility parallel to and perpendicular to the cleavage planes. Thus, unaligned polycrystalline specimens are bound to be inferior to aligned crystals, with ZT closer to 0.5 than 1. Nevertheless, such polycrystalline material is attractive from the practical viewpoint. It has been usual to select n-type materials from the Bi2Te3-Bi2Se3 system, but it should not be forgotten that suitably doped samples in the Bi2Te3-Sb2Te3 system will also be n-type. Thus, the properties of n-type BixSb2−xTe3, with x between 0.5 and 0.7, have been studied by Gerovac et al. [41] with a view to their use in generators. The figure of merit of these alloys is no larger than that of the Bi2Te3-Bi2Se3 alloys and, in view of their increased energy gap, the latter would appear to be the more promising for higher temperature use. It is expected that the best n-type materials will display some preferential orientation, the most practical production process, for achieving this end, involving hot extrusion [42,43].
Nanostructured bismuth telluride has been investigated at temperatures up to 430 K by Yu et al. [44]. The samples were prepared, by either spark plasma sintering or a high temperature—high pressure process, from hydrothermally produced nanorods. The rather low Seebeck coefficient, 130 to 150 μV/K at room temperature, suggests that the material could well be optimized for high temperature use. However, as acknowledged by the authors, their samples were inhomogeneous and there is evidence of mixed conduction from the thermal conductivity data. The low values of ZT between 0.4 and 0.5 do not necessarily mean that this type of processing will always yield poor material.
Good p-type material seems to have been produced by Li et al. [45]. Bulk nanostructured samples of a p-type (Bi-Sb)2Te3 alloy have been made by mechanical alloying and spark plasma sintering. The measurements covered the temperature range up to 580 K and included heavily doped material in which the Seebeck coefficient rose continuously with temperature. ZT was found to be 1.39 at 370 K so the material certainly seems suitable for use just above room temperature. However, it is noted that the acceptor impurity was copper, which has often been found to behave as a donor, when it lies between loosely bonded tellurium layers in the crystal lattice. In these interstitial positions it is a rapid diffuser even at room temperature [46]. Nevertheless, other workers [47] have also reported useful thermoelectric properties from copper- and silver-doped material.
One of the few papers to describe the properties of nanostructured material above room temperature has been published by Bulat et al. [48]. The material was p-type with the composition Bi0.4Sb1.6Te3. The high figure of merit, ZT, equal to 1.25 at about 100 °C, is attributed to a very small lattice conductivity. The sintered material was prepared from powders with a grain size of the order of 100 nm. The importance of the structure of the powders in any sintering process is apparent from the work of Wu et al. [49]. The best results were achieved using flower-like nanosheets yielding ZT of the order of unity over the whole temperature range 300 K to 525 K. Somewhat higher values of ZT were obtained by Xie et al. [50] who combined melt spinning and spark plasma sintering. A ZT value of 1.5 at 400 K was found for p-type Bi0.5Sb1.5Te3 but when the same techniques were applied to n-type Bi2(Te1−ySey)3 they yielded a ZT value of only 1.0. This, of course, may be an acceptable figure but it could, no doubt, be improved by orienting the grains, perhaps by extrusion.
Most of the early studies of sintered Bi2Te3 alloys made use of large particle sizes to minimize the effect of oxidation [51]. On the other hand, very fine powders are needed in the production of nanostructured material. This problem has been tackled successfully by Nguyen et al. [52] using a spark erosion technique. Samples of p-type Bi0.5Sb1.5Te3 made by sintering these powders have yielded a ZT value of 1.36 at 360 K.
Non-aligned n-type material with the formula LixBi2Se0.3Te2.7 has been prepared by Chen et al. [53] using a sintering method. The authors claim that the use of Li as a dopant improves ZT by about 25%. However, the observed value of 0.8, while quite high for non-aligned material, is no better than other workers have achieved. A significant feature of this work is the maintenance of a reasonably high ZT value up to a temperature of 500 K.
Kim et al. [54] produced n-type nanocomposites of bismuth seleno-telluride by introducing Bi2Se3 nanoparticle inclusions into bulk Bi2Te3. The reduction in the lattice conductivity was reflected in a rise of ZT at 320 K from 0.56 to 0.75. Measurement of the thermoelectric properties covered temperatures up to nearly 600 K. However, ZT fell continuously with increasing temperature over the whole range. This was largely because the Seebeck coefficient was continuously decreasing. That this should have occurred with a Seebeck coefficient of no more than −150 μV/K at 320 K is entirely unexpected and may indicate non-uniformity of composition. Part of the sample could have displayed mixed conduction and part extrinsic conduction, both regions having a low Seebeck coefficient.
Figures 3 and 4 summarize the results of the various authors that have been mentioned in this review. It must be remembered that the accurate measurement of the figure of merit is not simple, particularly at elevated temperatures. Typically [55], the error in determining this quantity may be as high as 20%. Thus, the highest and lowest values in these diagrams may not respectively indicate exceptionally good or bad material.
4. Practical Considerations
Thermoelectric refrigerators almost invariably make use of linear flow in multi-couple modules but for thermoelectric generation other geometric configurations may be preferred. Thus, a tubular arrangement is particularly suitable for harvesting the energy from fluid heat sources. It must be remembered that one of the earliest applications of thermoelectric generation, using an oil burner as the heat source, adopted this type of arrangement [2]. However, if a tubular configuration is sought, this may be more easily achieved using the transverse rather than the longitudinal Seebeck effect [56]. A transverse thermoelement is probably best produced from a synthetic two-phase material [12]. A thermoelectric generator, using the transverse Seebeck effect in a synthetic transverse material comprising p-type Bi0.5Sb1.5Te3 and Ni, has been described by Sakai et al. [57]. The figure of merit would have been close to that of a longitudinal (Bi-Sb)2Te3—Ni thermocouple. Other combinations would probably be superior, perhaps with the nickel being replaced by an n-type conductor such as bismuth, though Kyarad and Lengfellner [58] used a metal, lead, in conjunction with a bismuth telluride in their transverse device.
Thermoelectric modules are usually made from n-type and p-type thermoelements joined by metallic bridges. Whether or not such bridges are employed, it is necessary to make electrical contact between the components and, for this purpose, metallization of the thermoelements and some type of solder is usually needed. A joining technique that is satisfactory for refrigeration modules may not be sufficiently stable at the elevated temperature in a generator. Li et al. [59] have shown that antimony is a suitable contact material for both bismuth-antimony telluride and bismuth seleno-telluride. The problem of contacts was solved by Kadhim et al. [60] using silver paste in their generator operating from a heat source at 523 K.
The stability of thermoelectric generators over long time periods is probably an essential requirement. Tellurium is a volatile element and its loss would severely affect the thermoelectric properties of the alloys. In this context, the use of protective coatings may be necessary. Tests have been made by Brostow et al. [61] on polymer coatings and it has been found that weight loss has then been prevented at temperatures of up to 500 °C. Ceramic coatings cracked under the same conditions.
For the time being, most experimental thermoelectric generators [62], that operate at relatively low temperatures, will make use of existing modules, perhaps selected from batches that have low Seebeck coefficients. Test systems for such modules, under the conditions at which the generators will be operated, have been developed [63].
The question of the availability of the component elements has not been addressed. In this context it may be noted that the cost and scarcity of tellurium may make alloys based on bismuth telluride unsuitable for large scale applications.
5. Conclusions
It has been firmly established that ZT at 300 K has a maximum value of 1.0 for large-grained p-type (Bi-Sb)2Te3 with a substantially higher value for nanostructured material. ZT is almost as high at 0.9 for aligned n-type Bi2(Se-Te)3 though a value closer to, say, 0.6 is more typical for randomly oriented polycrystalline samples. By preparing samples with an increased carrier concentration and, therefore, a lower Seebeck coefficient, ZT can be maintained at similar values up to about 100 °C with a gradual decrease at still higher temperatures.
An increase of the energy gap would give some benefit at room temperature and would enable substantial improvements to be made above 300 K. It seems to be well established that Eg is greater for Bi2(Se-Te)3 than for Bi2Te3, so minority carrier conduction should be less of a problem for n-type alloys than for p-type material. It is possible that, because of the increased gap, Bi2(Se-Te)3 could also be superior to (Bi-Sb)2Te3 as a p-type generator material, provided that sufficient acceptor impurity can be accommodated. There has also been the suggestion that Sb2Te3 may have a larger energy gap than Bi2Te3 and, if this is so, (Bi-Sb)2Te3 with a reduced bismuth concentration may be preferred for generator applications. The non-stoichiometry of Sb2Te3 may prove to be an advantage in making p-type thermoelements for high temperature use.
Failing any increase in the energy gap, some energy filtering mechanism may allow the Seebeck coefficient to remain high at elevated temperatures, without appreciable minority carrier conduction. The resonant levels associated with tin in bismuth telluride and its alloys may be useful in this way, though the original studies [27] did not deal with the Seebeck coefficient as a function of temperature. Likewise, although there would undoubtedly be benefits for generator materials arising from a moderate amount of ionized-impurity scattering, experimental work to support this concept is lacking.
Figure 5 shows the variation of efficiency with ZT for a typical low grade heat source. The system that is envisaged would provide a modest amount of electrical power together with an ample supply of hot water. The heat source is supposed to be at 400 K and the heat sink to take the form of water at 360 K. The plot shows that a generation efficiency of about 2% should be attainable without any further material developments. The efficiency for a Carnot cycle operating between the same source and sink temperatures would be 10%. Efficiencies of the order of 20% of the Carnot cycle value are, in fact, typical for thermoelectric generators over a wide range of temperature.
In summary, it should be possible to produce both p-type and n-type bismuth telluride alloys that maintain a value of ZT equal to at least unity up to a temperature of 500 K, with a reasonable likelihood of obtaining significantly greater values over at least part of the temperature range. It is likely that the material will have a composition with a larger energy gap than that of bismuth telluride. Otherwise, minority carrier effects may be minimized by the addition of impurities, such as tin, with resonant states, or by the introduction of ionized-impurity scattering. Improved material is likely to have a bulk nanostructure with the n-type material displaying substantial preferred orientation, possibly achieved by an extrusion technique.
Acknowledgments
The author wishes to acknowledge helpful advice from Jeff Sharp in the preparation of this paper.
Conflicts of Interest
The author declares no conflict of interest.
References
- Goldsmid, H.J.; Douglas, R.W. The use of semiconductors in thermoelectric refrigeration. Brit. J. Appl. Phys 1954. [Google Scholar]
- Ioffe, A.F. Semiconductor Thermoelements and Thermoelectric Cooling; Infosearch: London, UK, 1957. [Google Scholar]
- Vedernikov, M.V.; Kuznetsov, V.L. Cooling thermoelements with superconducting leg. In CRC Handbook of Thermoelectrics; Rowe, D.M., Ed.; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Goldsmid, H.J.; Gopinathan, K.K.; Matthews, D.N.; Taylor, K.N.R.; Baird, C.A. High-Tc superconductors as passive thermo-elements. J. Phys. D 1988, 21, 344–348. [Google Scholar]
- Rosi, F.D.; Abeles, B.; Jensen, R.V. Materials for thermoelectric refrigeration. J. Phys. Chem. Solids 1959, 10, 191–200. [Google Scholar]
- Hicks, L.D.; Dresselhaus, M.S. Effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. B 1993, 47, 12727–12731. [Google Scholar]
- Venkatasubramanian, R.; Silvola, E.; Colpits, T.; O’Quinn, B. Thin-film thermoelectric devices with high room-temperature figures of merit. Nature 2001, 413, 597–602. [Google Scholar]
- Touzelbaev, M.N.; Zhou, P.; Venkatasubramanian, R.; Goodson, K.E. Thermal characterization of Bi2Te3/Sb2Te3 superlattices. J. Appl. Phys 2001. [Google Scholar]
- Drabble, J.R.; Goodman, C.H.L. Chemical bonding in bismuth telluride. J. Phys. Chem. Solids 1958, 5, 142–144. [Google Scholar]
- Goldsmid, H.J. The thermal conductivity of bismuth telluride. Proc. Phys. Soc. B 1956, 69, 203–209. [Google Scholar]
- Delves, R.T.; Bowley, A.E.; Hazelden, D.W.; Goldsmid, H.J. Anisotropy of the electrical conductivity in bismuth telluride. Proc. Phys. Soc 1961, 78, 838–844. [Google Scholar]
- Goldsmid, H.J. Introduction to Thermoelectricity; Springer: Berlin, Germany, 2010. [Google Scholar]
- Bhandari, C.M.; Rowe, D.M. Thermal Conduction in Semiconductors; Wiley Eastern: New Delhi, India, 1988. [Google Scholar]
- Goldsmid, H.J. The electrical conductivity and thermoelectric power of bismuth telluride. Proc. Phys. Soc 1958, 71, 633–646. [Google Scholar]
- Austin, I.G. The optical properties of bismuth telluride. Proc. Phys. Soc 1958, 72, 545–552. [Google Scholar]
- Greenaway, D.L.; Harbeke, G. Band structure of bismuth telluride, bismuth selenide and their respective alloys. J. Phys. Chem. Solids 1965, 26, 1585–1604. [Google Scholar]
- Goldsmid, H.J.; Sharp, J.W. Estimation of the thermal band gap of a semiconductor from Seebeck measurements. J. Electron. Mater 1999, 28, 869–872. [Google Scholar]
- Muller, E.; Heiliger, W.; Reinshaus, P.; Sussman, H. Determination of the thermal band gap from the change of the Seebeck coefficient at the pn-transition in Bi0.5Sb1.5Te3, Proceedings of the 15th IEEE International Conference on Thermoelectrics, Pasadena, CA, USA, 26–29 March 1996.
- Kane, E.O. Band structure of indium antimonide. J. Phys. Chem. Solids 1957, 1, 249–261. [Google Scholar]
- Berger, L.I. Semiconducting properties of selected materials. In CRC Handbook of Chemistry and Physics, 91st ed; CRC Press: Cleveland, OH, USA, 2010. [Google Scholar]
- Veis, A.N.; Luk’yanova, L.N.; Kutasov, V.A. Band gap and type of optical transitions at the interband absorption edge in solid solutions based on bismuth telluride. Phys. Solid State 2012, 54, 2182–2188. [Google Scholar]
- Yim, W.M.; Rosi, F.D. Compound tellurides and their alloys for Peltier cooling—A review. Solid. State Electron 1972, 15, 1121–1140. [Google Scholar]
- Zheng, Z.H.; Fan, P.; Luo, J.T.; Liang, G.X.; Zhang, D.P. Enhanced thermoelectric properties of antimony telluride thin films with preferred orientation prepared by sputtering a fan-shaped binary composite target. J. Electron. Mater 2013, 42, 3421–3425. [Google Scholar]
- Sun, S.; Peng, J.; Jin, R.; Song, S.; Zhu, P.; Xing, Y. Template-free solvothermal synthesis and enhanced thermoelectric performance of Sb2Te3 nanosheets. J. Alloy. Compd 2013, 558, 6–10. [Google Scholar]
- Mehta, R.J.; Zhang, Y.; Zhu, H.; Parker, D.S.; Belley, M.; Singh, D.J.; Ramprasad, R.; Borca-Tasciuc, T.; Ramanath, G. Seebeck and figure of merit enhancement in nanostructured antimony telluride by antisite defect suppression through sulfur doping. Nanoletters 2012, 12, 4523–4529. [Google Scholar]
- Heremans, J.P.; Jovovic, V.; Toberer, E.S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G.J. Enhancement of thermoelectric efficiency in PbTe by distortion of the electronic density of states. Science 2008, 321, 554–557. [Google Scholar]
- Jaworski, C.M.; Kulbachinskii, V.; Heremans, J.P. Resonant level formed by tin in Bi2Te3 and the enhancement of room-temperature thermoelectric power. Phys. Rev. B 2009, 233201. [Google Scholar]
- Goldsmid, H.J. Effect of the scattering law on the maximum Seebeck coefficient. J. Thermoelectr 2006, 2, 5–8. [Google Scholar]
- Goldsmid, H.J.; Cochrane, J.W. Solar thermoelectric generators, Proceedings of the 4th IEEE International Conference on Thermoelectric Energy Conversion, Arlington, TX, USA, 10–12 March 1982.
- Imamuddin, M.; Dupre, A. Thermoelectric properties of p-type Bi2Te3-Sb2Te3-Sb2Se3 alloys and n-type Bi2Te3-Bi2Se3 alloys in the temperature range 300 to 600 K. Phys. Stat. Solidi A 1972, 10, 415–424. [Google Scholar]
- Scherrer, H.; Scherrer, S. Thermoelectric properties of bismuth antimony telluride solid solutions. In Thermoelectrics Handbook: Macro to Nano; Rowe, D.M., Ed.; CRC Taylor and Francis: Boca Raton, FL, USA, 2012. [Google Scholar]
- Scherrer, H.; Scherrer, S. Bismuth telluride, antimony telluride and their solid solutions. In CRC Handbook of Thermoelectrics; Rowe, D.M., Ed.; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Snyder, G.J. Thermoelectric power generation: Efficiency and compatibility. In Thermoelectrics Handbook: Macro to Nano; Rowe, D.M., Ed.; CRC Taylor and Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Kutasov, V.A.; Lukyanova, L.N.; Vedernikov, M.V. Shifting the maximum figure of merit of (Bi,Sb)2(Te,Se)3 thermoelectrics to lower temperatures. In Thermoelectrics Handbook: Macro to Nano; Rowe, D.M., Ed.; CRC Taylor and Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Son, J.H.; Oh, M.W.; Kim, B.S.; Park, S.D.; Min, B.K.; Kim, M.H.; Lee, H.W. Effect of ball milling time on the thermoelectric properties of p-type (Bi,Sb)2Te3. J. Alloy. Compd 2013, 566, 168–174. [Google Scholar]
- Kuznetsov, V.L. Functionally graded materials for thermoelectric applications. In Thermoelectrics Handbook: Macro to Nano; Rowe, D.M., Ed.; CRC Taylor and Francis: Boca Raton, FL, USA, 2012. [Google Scholar]
- Min, G.; Rowe, D.M. Peltier devices as generators. In CRC Handbook of Thermoelectrics; Rowe, D.M., Ed.; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Matsuura, K.; Rowe, D.M. Low-temperature heat conversion. In CRC Handbook of Thermoelectrics; Rowe, D.M., Ed.; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Dashevsky, Z.; Drabkin, I.; Korotaev, V.; Rabinovich, D. Improved materials for thermoelectric conversion (generation), Proceedings of the 16th IEEE International Conference on Thermoelectrics, Dresden, Free State, Germany, 26–29 August 1997.
- Kusano, D.; Hori, Y. Effects of PbTe doping on the thermoelectric properties of (Bi2Te3)0.2(Sb2Te3)0.8, Proceedings of the 21st IEEE International Conference on Thermoelectrics, Long Beach, CA, USA, 25–29 August 2002.
- Gerovac, N.; Snyder, G.J.; Caillat, T. Thermoelectric properties of n-type polycrystalline Bix Sb2−x Te3 alloys, Proceedings of the 21st IEEE International Conference on Thermoelectrics, Long Beach, CA, USA, 25–29 August 2002.
- Bogomolov, D.I.; Bublik, V.T.; Skipidarov, S.Y.; Tabachkova, N.Y. Structure and properties of thermoelectric materials based on Bi2(SeTe)3 and (BiSb)2Te3 solid solutions prepared by equal-channel angular pressing. Inorg. Mater 2013, 49, 758–775. [Google Scholar]
- Keshavarz, M.K.; Vasilevskiy, D.; Masut, R.A.; Turenne, S. p-type bismuth telluride-based composite thermoelectric materials produced by mechanical alloying and how extrusion. J. Electron. Mater 2013, 42, 1429–1435. [Google Scholar]
- Yu, C.; Zhang, X.; Leng, M.; Shaga, A.; Liu, D.; Chen, F.; Wang, C. Preparation and thermoelectric properties of inhomogeneous bismuth telluride alloyed nanorods. J. Alloy. Compd 2013, 570, 86–93. [Google Scholar]
- Li, H.; Jing, H.; Han, Y.; Xu, Y.; Lu, G.Q.; Xu, L. Microstructure and transport properties of copper-doped p-type (BiSbTe) alloy prepared by mechanical alloying and subsequent spark plasma sintering. J. Alloy. Compd 2013, 576, 369–374. [Google Scholar]
- Carlson, R.O. Anisotropic diffusion of copper into bismuth telluride. J. Phys. Chem. Solids 1960, 13, 65–70. [Google Scholar]
- Lee, K.H.; Kim, H.S.; Kim, S.I.; Lee, E.S.; Lee, S.M.; Rhyee, J.S.; Jung, J.Y.; Kim, I.H.; Wang, Y.F.; Koumoto, K. Enhancement of thermoelectric figure of merit for Bi0.5Sb1.5Te3 by metal nanoparticle decoration. J. Electron. Mater 2012, 41, 1165–1169. [Google Scholar]
- Bulat, L.P.; Drabkin, I.A.; Karatayev, V.V.; Osvenskii, V.B.; Parkhomenko, Y.N.; Lavrentev, M.G.; Sorokin, A.I.; Pshenai-Severin, D.A.; Blank, V.D.; Pivovarov, G.I.; et al. Structure and transport properties of bulk nanothermoelectrics based on Bix Sb2−x Te3 fabricated by SPS method. J. Electron. Mater 2013, 42, 2110–2113. [Google Scholar]
- Wu, F.; Song, H.; Gao, F.; Shi, W.; Jia, J.; Hu, X. Effects of different morphologies of Bi2Te3 nanopowders on thermoelectric properties. J. Electron. Mater 2013, 42, 1140–1145. [Google Scholar]
- Xie, W.; Wang, S.; Zhu, S.; Ho, J.; Tang, X.; Zhang, Q.; Tritt, T.M. High performance Bi2Te3 nanocomposites prepared by single-element-melt-spinning spark-plasma sintering. J. Mater. Sci 2013, 48, 2745–2760. [Google Scholar]
- Cope, R.G.; Penn, A.W. The powder metallurgy of n-type Bi2Te2.55Se0.45 thermoelectric material. J. Mater. Sci 1968, 3, 103–109. [Google Scholar]
- Nguyen, P.K.; Lee, K.H.; Moon, J.; Kim, S.I.; Ahn, K.A.; Chen, L.H.; Lee, S.M.; Chen, R.K.; Jin, S.; Berkowitz, A.E. Spark erosion: A high production rate method for producing Bi0.5Sb1.5Te3 nanoparticles with enhanced thermoelectric performance. Nanotechnology 2012, 23, 415604–415610. [Google Scholar]
- Chen, J.; Zhou, X.; Uher, C.; Shi, X.; Jun, J.; Dong, H.; Li, Y.; Zhou, Y.; Wen, Z.; Chen, L. Structural modifications and non-monotonic carrier concentration in Bi2Se0.3Te2.7 by reversible electrochemical lithium reactions. Acta Mater 2013, 61, 1508–1517. [Google Scholar]
- Kim, H.; Han, M.K.; Yo, C.H.; Lee, W.; Kim, S.J. Effects of Bi2Se3 nanoparticle inclusions on the microstructure and thermoelectric properties of Bi2Te3-based nanocomposites. J. Electron. Mater 2012, 41, 3411–3416. [Google Scholar]
- Sharp, J.W. Marlow Industries: Dallas, TX, USA; Private Communication; 2014. [Google Scholar]
- Anatychuk, L.I. Thermoelectric Power Convertors; Institute of Thermoelectricity: Kiev, Ukraine, 2005. [Google Scholar]
- Sakai, A.; Kanno, T.; Takahashi, K.; Tamaki, H.; Adachi, H.; Yamada, Y. Enhancement in performance of the tubular thermoelectric generator (TTEG). J. Electron. Mater 2013, 42, 1612–1616. [Google Scholar]
- Kyarad, A.; Lengfellner, H. Transverse Peltier effect in tilted Pb-Bi2Te3 multilayer structures. Appl. Phys. Lett 2006, 192103. [Google Scholar]
- Li, F.; Huang, X.; Jiang, W.; Chen, L. Interface microstructure and performance of Sb contacts in bismuth telluride-based thermoelectric elements. J. Electron. Mater 2013, 42, 1219–1224. [Google Scholar]
- Kadhim, A.; Hmood, A.; Abu Hassan, H. Electrical characterization of thermoelectric genrators based on p-type Bi0.4Sb1.6Se2.4Te0.6 and n-type Bi2Se0.6Te2.4 bulk thermoelectric materials. Mater. Lett 2013, 97, 24–26. [Google Scholar]
- Brostow, W.; Datashvili, T.; Lobland, H.E.H.; Hilbig, T.; Su, L.; Vinado, C.; White, J. Bismuth telluride-based thermoelectric materials: Coating as protection against thermal cycling effects. J. Mater. Res 2012, 27, 2930–2936. [Google Scholar]
- Zhang, M.; Miao, L.; Kang, Y.P.; Tanemura, S.; Fisher, C.A.J.; Xu, G.; Li, C.X.; Fan, G.Z. Efficient, low-cost solar thermoelectric cogenerators comprising evacuated tubular solar collectors and thermoelectric modules. Appl. Energy 2013, 109, 51–59. [Google Scholar]
- Faraji, A.Y.; Akbarzadeh, A. Design of a compact, portable test system for thermoelectric power generator modules. J. Electron. Mater 2013, 42, 1535–1541. [Google Scholar]





| Type | σ at 150 K | σ at 300 K | Ratio of conductivities at 300 and 150 K |
|---|---|---|---|
| n | 1.5 × 103 Ω−1·cm−1 | 1.655 × 103 Ω−1 cm−1 | 1.10 |
| p | 1.55 × 103 Ω−1 cm−1 | 1.4 × 103 Ω−1 cm−1 | 0.90 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Goldsmid, H.J. Bismuth Telluride and Its Alloys as Materials for Thermoelectric Generation. Materials 2014, 7, 2577-2592. https://doi.org/10.3390/ma7042577
Goldsmid HJ. Bismuth Telluride and Its Alloys as Materials for Thermoelectric Generation. Materials. 2014; 7(4):2577-2592. https://doi.org/10.3390/ma7042577
Chicago/Turabian StyleGoldsmid, H. Julian. 2014. "Bismuth Telluride and Its Alloys as Materials for Thermoelectric Generation" Materials 7, no. 4: 2577-2592. https://doi.org/10.3390/ma7042577
APA StyleGoldsmid, H. J. (2014). Bismuth Telluride and Its Alloys as Materials for Thermoelectric Generation. Materials, 7(4), 2577-2592. https://doi.org/10.3390/ma7042577