Raman and Conductivity Analysis of Graphene for Biomedical Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Equipment
2.2. Drude Theoretical Approach
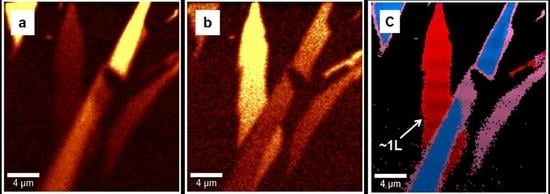
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Niyogi, S.; Bekyarova, E.; Hong, J.; Khizroev, S.; Berger, C.; De Heer, W.; Haddon, R.C. Covalent Chemistry for Graphene Electronics. J. Phys. Chem. Lett. 2011, 2, 2487–2498. [Google Scholar] [CrossRef]
- Bao, Q.; Loh, K.P. Graphene Photonics, Plasmonics, and Broadband Optoelectronic Devices. ACS Nano 2012, 6, 3677–3694. [Google Scholar] [CrossRef] [PubMed]
- Vicarelli, L.; Heerema, S.J.; Dekker, C.; Zandbergen, H.W. Controlling Defects in Graphene for Optimizing the Electrical Properties of Graphene Nanodevices. ACS Nano 2015, 9, 3428–3435. [Google Scholar] [CrossRef] [PubMed]
- Cocchi, C.; Prezzi, D.; Ruini, A.; Caldas, M.J.; Molinari, E. Electronics and Optics of Graphene Nanoflakes: Edge Functionalization and Structural Distortions. J. Phys. Chem. C 2012, 116, 17328–17335. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Z.; Huang, Y.; Ma, Y.; Wang, C.; Chen, M.; Chen, Y. Supercapacitor Devices Based on Graphene Materials. J. Phys. Chem. C 2009, 113, 13103–13107. [Google Scholar] [CrossRef]
- Luo, G.; Liu, L.; Zhang, J.; Li, G.; Wang, B.; Zhao, J. Hole Defects and Nitrogen Doping in Graphene: Implication for Supercapacitor Applications. ACS Appl. Mater. Interfaces 2013, 5, 11184–11193. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S.; Kim, S.I.; Yoon, J.C.; Jang, J.H. Chemical Vapor Deposition of Mesoporous Graphene Nanoballs for Supercapacitor. ACS Nano 2013, 7, 6047–6055. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Kim, J.; Kim, K.; Kim, S.Y.; Cheong, W.H.; Park, K.; Song, J.H.; Namgoong, G.H.; Kim, J.J.; Heo, J.; et al. Wearable, wireless gas sensors using highly stretchable and transparent structures of nanowires and graphene. Nanoscale 2016, 8, 10591–10597. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, M.S.; Jeon, S.; Kim, M.; Kim, S.; Kim, K.; Bien, F.; Hong, S.Y.; Park, J.U. Highly Tansparent and Streatchable Field-Effect Transistor Sensors Using Graphene-Nanowire Hybrid nanostructures. Adv. Mater. 2015, 27, 3292–3297. [Google Scholar] [CrossRef] [PubMed]
- Kravets, V.G.; Schedin, F.; Jalil, R.; Britnell, L.; Novoselov, K.S.; Grigorenko, A.N. Surface Hydrogenation and Optics of a Graphene Sheet Transferred onto a Plasmonic Nanoarray. J. Phys. Chem. C 2012, 116, 3882–3887. [Google Scholar] [CrossRef]
- Hadad, Y.; Davoyan, A.R.; Engheta, N.; Steinberg, B.Z. Extreme and Quantized Magneto-Optics with Graphene Meta-Atoms and Metasurfaces. ACS Photonics 2014, 1, 1068–1073. [Google Scholar] [CrossRef]
- Fang, Z.; Liu, Z.; Wang, Y.; Ajayan, P.M.; Nordlander, P.; Halas, N.J. Graphene-Antenna Sandwich Photodetector. Nano Lett. 2012, 12, 3808–3813. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, Y.; Deng, W.Q.; Goddard, W.A. Contact Resistance for “End-Contacted” Metal-Graphene and Metal-Nanotube Interfaces from Quantum Mechanics. J. Phys. Chem. C 2010, 114, 17845–17850. [Google Scholar] [CrossRef]
- Lee, C.K.; Hwangbo, Y.; Kim, S.M.; Lee, S.K.; Lee, S.M.; Kim, S.S.; Kim, K.S.; Lee, H.J.; Choi, B.I.; Song, C.K.; et al. Monatomic Chemical-Vapor-Deposited Graphene Membranes Bridge a Half-Millimeter-Scale Gap. ACS Nano 2014, 8, 2336–2344. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.; Klimov, N.N.; Solares, S.D.; Li, T.; Xu, H.; Cannara, R.J. Nanoscale Interfacial Friction and Adhesion on Supported versus Suspended Monolayer and Multilayer Graphene. Langmuir 2013, 29, 235–243. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Cai, X.; Wang, X.; Gao, C.; Liu, S.; Gao, F.; Wang, Q. Highly sensitive and selective detection of dopamine in the presence of ascorbic acid at graphene oxide modified electrode. Sens. Actuators B Chem. 2013, 186, 380–387. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.M.; Tang, L.H.; Lu, J.; Li, J.H. Application of graphene-modified electrode for selective detection of dopamine. Electrochem. Commun. 2009, 11, 889–892. [Google Scholar] [CrossRef]
- Shan, C.S.; Yang, H.F.; Song, J.F.; Han, D.X.; Ivaska, A.; Niu, L. Direct electrochemistry of glucose oxidase and biosensing for glucose based on graphene. Anal. Chem. 2009, 81, 2378–2382. [Google Scholar] [CrossRef] [PubMed]
- Pumera, M. Graphene in biosensing. Mater. Today 2011, 7–8, 308–315. [Google Scholar] [CrossRef]
- Malard, L.M.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473, 51–87. [Google Scholar] [CrossRef]
- Jang, W.; Chen, Z.; Bao, W.; Lau, C.N.; Dames, C. Thickness-Dependent Thermal Conductivity of Encased Graphene and Ultrathin Graphite. Nano Lett. 2010, 10, 3909–3913. [Google Scholar] [CrossRef] [PubMed]
- Kholmanov, I.N.; Magnuson, C.W.; Aliev, A.E.; Li, H.; Zhang, B.; Suk, J.W.; Zhang, L.L.; Peng, E.; Mousavi, S.H.; Khanikaev, A.B.; et al. Improved Electrical Conductivity of Graphene Films Integrated with Metal Nanowires. Nano Lett. 2012, 12, 5679–5683. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Yu, X.; Hu, W.; Wu, X.; Zhao, Y.; Yang, D. An 8.68% Efficiency Chemically-Doped-Free Graphene-Silicon Solar Cell Using Silver Nanowires Network Buried Contacts. ACS Appl. Mater. Interfaces 2015, 7, 4135–4141. [Google Scholar] [CrossRef] [PubMed]
- Dou, L.; Cui, F.; Yu, Y.; Khanarian, G.; Eaton, S.W.; Yang, Q.; Resasco, J.; Schildknecht, C.; Schierle-Arndt, K.; Yang, P. Solution-Processed Copper/Reduced-Graphene-Oxide Core/Shell Nanowire Transparent Conductors. ACS Nano 2016, 10, 2600–2606. [Google Scholar] [CrossRef] [PubMed]
- Stankovich, S.; Dikin, D.A.; Dommett, H.B.; Kohlhass, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282–285. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Muller, M.B.; Gilmore, K.L.; Wallace, G.G.; Li, D. Mechanically Strong, Ellectrically Conductive, and Biocompatable Graphene Paper. Adv. Mater. 2008, 20, 3557–3561. [Google Scholar] [CrossRef]
- Zhu, J.; Wei, S.; Rapole, S.B.; Gu, H.; Luo, Z.; Haldolaarachchige, N.; Young, D.P.; Guo, Z. One-pot Synthesis of Magnetic Graphene Nanocomposites Decorated with Core@Double-shell Nanoparticles for Fast Chromium Removal. Environ. Sci. Technol. 2012, 46, 977–985. [Google Scholar] [CrossRef] [PubMed]
- Cataldo, F.; Ursini, O.; Angelini, G.; Igleisas-Groth, S. On the way to Graphene: The Bottom-Up Approach to Very Large PAHs Using the Scholl reaction. Fuller. Nanotub. Carbon Nanostruct. 2011, 19, 713–725. [Google Scholar] [CrossRef]
- Cong, C.; Ting, Y. Enhanced ultra-low frequency interlayer shear modes in folded graphene layers. Nat. Commun. 2014, 5, 4709. [Google Scholar] [CrossRef] [PubMed]
- Glover, R.E., III; Tinkham, M. Conductivity of Superconducting Films for Photon Energies between 0.3 and 40 kTc. Phys. Rev. Lett. 1957, 108, 243–256. [Google Scholar]
- Liu, H.L.; Quijada, M.; Romero, B.D.; Tanner, D.B.; Zibold, A.; Carr, G.L.; Berger, H.; Forro, L.; Mihaly, L.; Cao, G.; et al. Drude behavior in the far-infrared conductivity of cuprate superconductors. Ann. Phys. 2006, 15, 606–618. [Google Scholar] [CrossRef]
- Horng, J.; Chen, C.F.; Geng, B.; Girit, C.; Zhang, Y.; Hao, Z.; Bechtel, H.A.; Martin, M.; Zettl, A.; Crommie, M.F.; et al. Drude conductivity of Dirac fermions in graphene. Phys. Rev. B 2011, 83, 165113. [Google Scholar] [CrossRef]
- Yan, H.; Li, X.; Chandra, B.; Tulevski, G.; Wu, Y.; Freitag, M.; Zhu, W.; Avouris, P.; Xia, F. Tunable infrared plasmonic devices using graphene/insulator stacks. Nat. Nanotechnol. 2012, 7, 330–334. [Google Scholar] [CrossRef] [PubMed]
- Manciu, F.S.; Manciu, M.; Durrer, W.G.; Salazar, J.; Lee, K.H.; Bennet, K.E. A Drude model analysis of conductivity and free carriers in boron-doped diamond films and investigations of their internal stress and strain. J. Mater. Sci. 2014, 49, 5782–5789. [Google Scholar] [CrossRef] [PubMed]
- Mak, K.F.; Ju, L.; Wang, F.; Heinz, T.F. Optical spectroscopy of graphene: From the far infrared to the ultraviolet. Solid State Commun. 2012, 152, 1341–1349. [Google Scholar] [CrossRef]
- Peres, N.M.R. The transport properties of graphene: An introduction. Rev. Mod. Phys. 2010, 82, 2673–2700. [Google Scholar] [CrossRef]
- Bennet, K.E.; Lee, K.H.; Kruchowski, J.N.; Chang, S.Y.; Marsh, M.P.; Van Orsow, A.A.; Paez, A.; Manciu, F.S. Development of Conductive Boron-Doped Diamond Electrode: A Microscopic, Spectroscopic, and Voltammetric Study. Materials 2013, 6, 5726–5741. [Google Scholar] [CrossRef]
- Bennet, K.E.; Tomshine, J.; Min, P.; Manciu, F.S.; Marsh, M.; Paek, B.; Settell, M.; Nicolai, E.; Blaha, C.D.; Kouzani, A.Z.; et al. A Diamond-Based Electrode for Detection of Neurotransmitters in the Human Brain. Front. Hum. Neurosci. 2016, 10, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Sutter, E.; Shi, N.N.; Zheng, J.; Yang, T.; Englund, D.; Gao, H.J.; Sutter, P. Reliable Exfoliation of Large-Area High-Quality Flakes of Graphene and Other Two-Dimensional Materials. ACS Nano 2015, 9, 10612–10620. [Google Scholar] [CrossRef] [PubMed]
- Tan, P.H.; Dimovski, S.; Gogotsi, Y. Raman scattering of non-planar graphite: Arched edges, polyhedral crystals, whiskers and cones. Phil. Trans. R. Soc. Lond. A 2004, 362, 2289–2310. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, A.C.; Basko, D.M. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Nanotechnol. 2013, 8, 235–246. [Google Scholar] [CrossRef] [PubMed]
- Cong, C.; Yu, T. Evolution of Raman G and G′ (2D) modes in folded graphene layers. Phys. Rev. B 2014, 89, 235430. [Google Scholar] [CrossRef]
- Tan, P.H.; Han, W.P.; Zhao, W.J.; Wu, Z.H.; Chang, K.; Wang, H.; Wang, Y.F.; Bonini, N.; Marzari, N.; Pugno, N.; et al. The shear mode of multilayer graphene. Nat. Mater. 2012, 11, 294–300. [Google Scholar] [CrossRef] [PubMed]
- Rademeyer, C.J.; Human, H.G.C.; Faure, P.K. The electrical resistivity of some graphite types as used in electrothermal atomic absorption spectrometry. Spectrochem. Acta Part B At. Spectrosc. 1983, 38, 945–948. [Google Scholar] [CrossRef]
- Hunag, S.; Ling, X.; Liang, L.; Song, Y.; Fang, W.; Zhang, J.; Kong, V.M.; Dresselhaus, M.S. Molecular Selectivity of Graphene-Enhanced Raman Scattering. Nano Lett. 2015, 15, 2892–2901. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Xia, M.; Liang, O.; Sun, K.; Cipriano, A.F.; Schroeder, T.; Liu, H.; Xie, Y.-H. Label-Free SERS Selective Detection of Dopamine and Serotonin Using Graphene-Au Nanopyramid Heterostructure. Anal. Chem. 2015, 87, 10255–10261. [Google Scholar] [CrossRef] [PubMed]
- Mohammad-Shiri, H.; Ghaemi, M.; Riahi, S.; Akbari-Sehat, A. Computational and Electrochemical Studies on the Redox Reaction of Dopamine in Aqueous Solution. Int. J. Electrochem. Sci. 2011, 6, 317–336. [Google Scholar]
- Qin, L.; Li, X.; Kang, S.-Z.; Mu, J. Gold nanoparticles conjugated dopamine as sensing platform for SERS detection. Colloids Surf. B Biointerfaces 2015, 126, 210–216. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Jiang, Y.; Ma, L.; He, Y.; Gao, J. Immobilization of Glucose Oxidase on Polydopamine-Functionalized Graphene Oxide. Appl. Biochem. Biotech. 2015, 175, 1007–1017. [Google Scholar] [CrossRef] [PubMed]





© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, C.; Bennet, K.E.; Khan, T.; Ciubuc, J.D.; Manciu, F.S. Raman and Conductivity Analysis of Graphene for Biomedical Applications. Materials 2016, 9, 897. https://doi.org/10.3390/ma9110897
Qiu C, Bennet KE, Khan T, Ciubuc JD, Manciu FS. Raman and Conductivity Analysis of Graphene for Biomedical Applications. Materials. 2016; 9(11):897. https://doi.org/10.3390/ma9110897
Chicago/Turabian StyleQiu, Chao, Kevin E. Bennet, Tamanna Khan, John D. Ciubuc, and Felicia S. Manciu. 2016. "Raman and Conductivity Analysis of Graphene for Biomedical Applications" Materials 9, no. 11: 897. https://doi.org/10.3390/ma9110897
APA StyleQiu, C., Bennet, K. E., Khan, T., Ciubuc, J. D., & Manciu, F. S. (2016). Raman and Conductivity Analysis of Graphene for Biomedical Applications. Materials, 9(11), 897. https://doi.org/10.3390/ma9110897