High Pressure Properties of a Ba-Cu-Zn-P Clathrate-I
Abstract
:1. Introduction
2. Results and Discussion
2.1. Crystal Structure
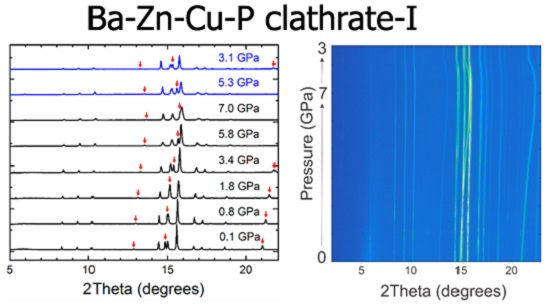
2.2. Synchrotron X-ray Powder Diffraction
2.3. Bulk Modulus Calculations
3. Experimental Section
3.1. Synthesis
3.2. High Pressure Synchrotron X-ray Powder Diffraction Collection and Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dolyniuk, J.; Owens-Baird, B.; Wang, J.; Zaikina, J.V.; Kovnir, K. Clathrate thermoelzectrics. Mat. Sci. Eng. R 2016, in press. [Google Scholar]
- Nolas, G.S. (Ed.) The Physics and Chemistry of Inorganic Clathrates; Springer: New York, NY, USA, 2014.
- Kovnir, K.; Stockert, U.; Budnyk, S.; Prots, Y.; Baitinger, M.; Paschen, S.; Shevelkov, A.V.; Grin, Y. Introducing a magnetic guest to a tetrel-free clathrate: Synthesis, structure, and properties of EuxBa8−xCu16P30 (0 ≤ x ≤ 1.5). Inorg. Chem. 2011, 50, 10387–10396. [Google Scholar] [CrossRef] [PubMed]
- Dolyniuk, J.; Wang, J.; Lee, K.; Kovnir, K. Twisted kelvin cells and truncated octahedral cages in the crystal structures of unconventional clathrates, AM2P4 (A = Sr, Ba; M = Cu, Ni). Chem. Mater. 2015, 27, 4476–4484. [Google Scholar] [CrossRef]
- Fulmer, J.; Lebedev, O.I.; Roddatis, V.V.; Kaseman, D.C.; Sen, S.; Dolyniuk, J.-A.; Lee, K.; Olenev, A.V.; Kovnir, K. Clathrate Ba8Au16P30: The “gold standard” for lattice thermal conductivity. J. Am. Chem. Soc. 2013, 135, 12313–12323. [Google Scholar] [CrossRef] [PubMed]
- Blancon, J.-C.; Machon, D.; Pischedda, V.; Debord, R.; Toulemonde, P.; le Floch, S.; Pascarelli, S.; M’elinon, P.; San-Miguel, A. Revisiting pressure-induced phase transition in silicon clathrates using Ge substitution. Phys. Rev. B 2016, 93. [Google Scholar] [CrossRef]
- Ovsyannikov, S.; Shchennikov, V. High-pressure routes in the thermoelectricity or how one can improve a performance of thermoelectrics. Chem. Mater. 2010, 22, 635–647. [Google Scholar] [CrossRef]
- Tsiok, O.; Khvostantsev, L.; Smirnov, I.; Golubkov, A.V. Electron and lattice stages in the valence transition in SmTe under a high hydrostatic pressure. J. Exp. Theor. Phys. 2005, 100, 752–759. [Google Scholar] [CrossRef]
- Dolyniuk, J.; Kovnir, K. University of California, Davis, CA, USA. Unpublished work. 2016. [Google Scholar]
- Toulemonde, P.; Machon, D.; San Miguel, A.; Amboage, M. High pressure X-ray diffraction study of the volume collapse in Ba24Si100 clathrate. Phys. Rev. B 2011, 83. [Google Scholar] [CrossRef]
- Machon, D.; Toulemonde, P.; McMillan, P.; Amboage, M.; Muñoz, A.; Rodríguez-Hernández, P.; San Miguel, A. High-pressure phase transformations, pressure-induced amorphization, and polyamorphic transition of the clathrate Rb6.15Si46. Phys. Rev. B 2009, 79, 184101. [Google Scholar] [CrossRef]
- Tse, J.; Desgreniers, S.; Li, Z.-Q.; Ferguson, M.; Kawazoe, Y. Structural stability and phase transitions in K8Si46 clathrate under high pressure. Phys. Rev. Lett. 2002, 89. [Google Scholar] [CrossRef] [PubMed]
- Murnaghan, F. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [PubMed]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71. [Google Scholar] [CrossRef]
- Angel, R.J.; Gonzalez-Platas, J.; Alvaro, M. EoSFit7c and a Fortran module (library) for equation of state calculations. Z. Kristallogr. 2014, 229, 405–419. [Google Scholar] [CrossRef]
- Gonzalez-Platas, J.; Alvaro, M.; Nestola, F.; Angel, R. EosFit7-GUI: A new GUI tool for equation of state calculations, analyses, and teaching. J. Appl. Cryst. 2016, in press. [Google Scholar] [CrossRef]
- Mingos, D.M.P. Essential Trends in Inorganic Chemistry; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Shevelkov, A.V.; Kovnir, K. Zintl clathrates. In Zintl Phases: Principles and Recent Developments; Fassler, T.F., Ed.; Springer: Berlin, Germany, 2011; pp. 97–142. [Google Scholar]
- Larson, A.; von Dreele, R. General Structure Analysis System (GSAS); Report LAUR 86-748; Los Alamos National Laboratory: Los Alamos, NM, USA, 2000; pp. 86–748. [Google Scholar]
- Toby, B. EXPGUI, a graphical user interface for GSAS. J. Appl. Cryst. 2001, 34, 210–213. [Google Scholar] [CrossRef]
- Toby, B.; von Dreele, R. GSAS-II: The genesis of a modern open-source all-purpose crystallography software package. J. Appl. Cryst. 2013, 46, 544–549. [Google Scholar] [CrossRef]
- Toby, B. CMPR—A powder diffraction toolkit. J. Appl. Cryst. 2005, 38, 1040–1041. [Google Scholar] [CrossRef]
- Angel, R. High-pressure structural phase transitions. In Transformation Processes in Minerals; Redfern, S.A.T., Carpenter, M.A., Eds.; Mineralogical Society of America: Chantilly, VA, USA, 2000; pp. 85–104. [Google Scholar]





© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dolyniuk, J.-A.; Kovnir, K. High Pressure Properties of a Ba-Cu-Zn-P Clathrate-I. Materials 2016, 9, 692. https://doi.org/10.3390/ma9080692
Dolyniuk J-A, Kovnir K. High Pressure Properties of a Ba-Cu-Zn-P Clathrate-I. Materials. 2016; 9(8):692. https://doi.org/10.3390/ma9080692
Chicago/Turabian StyleDolyniuk, Juli-Anna, and Kirill Kovnir. 2016. "High Pressure Properties of a Ba-Cu-Zn-P Clathrate-I" Materials 9, no. 8: 692. https://doi.org/10.3390/ma9080692
APA StyleDolyniuk, J. -A., & Kovnir, K. (2016). High Pressure Properties of a Ba-Cu-Zn-P Clathrate-I. Materials, 9(8), 692. https://doi.org/10.3390/ma9080692