TransPCGC: Point Cloud Geometry Compression Based on Transformers
Abstract
:1. Introduction
- We design a novel Transformer-based network for compressing geometric information in point clouds. This network comprises preprocessing modules for voxelization and partitioning of point clouds, compression networks to optimize the BD-Rate, and postprocessing modules for point cloud reconstruction. In contrast to pure convolutional neural networks, our designed network achieves remarkable compression gains.
- The effectiveness of point cloud compression is hindered due to convolutions designed with fixed receptive fields and fixed weights, which cannot aggregate enough information from sparse and disordered point clouds. There is a need for a solution that can better exploit correlations among global and local information point clouds. As the Transformer architecture designed for processing images is not well suited for point clouds, we develop a Transformer capable of handling point clouds. Utilizing this Transformer, we extract the richness of both global and local features from the point cloud.
- Extensive experiments validate the compression performance of the proposed TransPCGC on multiple point cloud datasets, while also demonstrating its low spatial and temporal complexity.
2. Related Work
2.1. Non-Deep Learning Methods
2.2. Deep Learning Methods
2.3. Transformer Methods
3. Methods
3.1. Pre-Processing
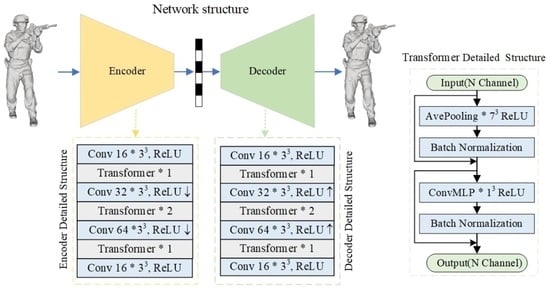
3.2. Encoder and Decoder Modules
Transformer Block
3.3. Entropy Coding
3.4. Loss Function
3.5. Post-Processing
4. Experiment
4.1. Experimental Set
4.2. Experiment Results
4.3. Ablation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, Z.; Peng, S.; Larsson, V.; Xu, W.; Bao, H.; Cui, Z.; Oswald, M.R.; Pollefeys, M. Nice-slam: Neural implicit scalable encoding for slam. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12786–12796. [Google Scholar]
- Li, Y.; Zhao, Z.; Fan, J.; Li, W. ADR-MVSNet: A cascade network for 3D point cloud reconstruction with pixel occlusion. Pattern Recognit. 2022, 125, 108516. [Google Scholar] [CrossRef]
- Fernandes, D.; Silva, A.; Névoa, R.; Simões, C.; Gonzalez, D.; Guevara, M.; Novais, P.; Monteiro, J.; Melo-Pinto, P. Point-cloud based 3D object detection and classification methods for self-driving applications: A survey and taxonomy. Inf. Fusion 2021, 68, 161–191. [Google Scholar] [CrossRef]
- Vujasinović, M.; Regodić, M.; Kecman, S. Point cloud processing software solutions. AGG+ J. Archit. Civ. Eng. Geod. Relat. Sci. Fields 2020, 8, 64–75. [Google Scholar] [CrossRef]
- Quach, M.; Valenzise, G.; Dufaux, F. Learning Convolutional Transforms for Lossy Point Cloud Geometry Compression. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 4320–4324. [Google Scholar] [CrossRef]
- Quach, M.; Valenzise, G.; Dufaux, F. Improved Deep Point Cloud Geometry Compression. In Proceedings of the 2020 IEEE 22nd International Workshop on Multimedia Signal Processing (MMSP), Tampere, Finland, 21–24 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, H.; Liu, H.; Ma, Z. Lossy Point Cloud Geometry Compression via End-to-End Learning. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4909–4923. [Google Scholar] [CrossRef]
- Wang, J.; Ding, D.; Li, Z.; Ma, Z. Multiscale Point Cloud Geometry Compression. In Proceedings of the 2021 Data Compression Conference (DCC), Snowbird, UT, USA, 23–26 March 2021; pp. 73–82. [Google Scholar] [CrossRef]
- Wang, J.; Ding, D.; Li, Z.; Feng, X.; Cao, C.; Ma, Z. Sparse Tensor-Based Multiscale Representation for Point Cloud Geometry Compression. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 9055–9071. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, D.T.; Quach, M.; Valenzise, G.; Duhamel, P. Learning-Based Lossless Compression of 3D Point Cloud Geometry. In Proceedings of the 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 4220–4224. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Quach, M.; Valenzise, G.; Duhamel, P. Multiscale deep context modeling for lossless point cloud geometry compression. In Proceedings of the 2021 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), Shenzhen, China, 5–9 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Quach, M.; Valenzise, G.; Duhamel, P. Lossless Coding of Point Cloud Geometry Using a Deep Generative Model. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4617–4629. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Kaup, A. Lossless Point Cloud Geometry and Attribute Compression Using a Learned Conditional Probability Model. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 4337–4348. [Google Scholar] [CrossRef]
- Guarda, A.F.R.; Rodrigues, N.M.M.; Pereira, F. Adaptive Deep Learning-Based Point Cloud Geometry Coding. IEEE J. Sel. Top. Signal Process. 2021, 15, 415–430. [Google Scholar] [CrossRef]
- Wang, J.; Ding, D.; Ma, Z. Lossless Point Cloud Attribute Compression Using Cross-scale, Cross-group, and Cross-color Prediction. In Proceedings of the 2023 Data Compression Conference (DCC), IEEE, Snowbird, UT, USA, 21–24 March 2023; pp. 228–237. [Google Scholar]
- Wiesmann, L.; Milioto, A.; Chen, X.; Stachniss, C.; Behley, J. Deep Compression for Dense Point Cloud Maps. IEEE Robot. Autom. Lett. 2021, 6, 2060–2067. [Google Scholar] [CrossRef]
- Liang, Z.; Liang, F. TransPCC: Towards Deep Point Cloud Compression via Transformers. In Proceedings of the 2022 International Conference on Multimedia Retrieval, Newark, NJ, USA, 27–30 June 2022; pp. 1–5. [Google Scholar]
- Huang, L.; Wang, S.; Wong, K.; Liu, J.; Urtasun, R. Octsqueeze: Octree-structured entropy model for lidar compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1313–1323. [Google Scholar]
- Beemelmanns, T.; Tao, Y.; Lampe, B.; Reiher, L.; van Kempen, R.; Woopen, T.; Eckstein, L. 3D Point Cloud Compression with Recurrent Neural Network and Image Compression Methods. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), IEEE, Aachen, Germany, 5–9 June 2022; pp. 345–351. [Google Scholar]
- ISO/IEC 23090-9:2023; Information Technology-Coded Representation of Immersive Media-Part 9: Geometry-Based Point Cloud Compression (G-PCC). MPEG: Kowloon, Hong Kong, 2023.
- ISO/IEC 23090-5:2021; Information Technology-Coded Representation of Immersive Media-Part 5: Visual Volumetric Vedio-Based Coding (V3C) and Vedio-Based Point Cloud Compression (V-PCC). MPEG: Kowloon, Hong Kong, 2021.
- Dvořák, J.; Káčereková, Z.; Vaněček, P.; Váša, L. Priority-based encoding of triangle mesh connectivity for a known geometry. Comput. Graph. Forum 2023, 42, 60–71. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3d is here: Point cloud library (pcl). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Huang, T.; Liu, Y. 3d point cloud geometry compression on deep learning. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 890–898. [Google Scholar]
- Google. Draco 3D Data Compression. 2017. Available online: https://github.com/google/draco (accessed on 15 October 2023).
- Dumic, E.; Bjelopera, A.; Nüchter, A. Dynamic point cloud compression based on projections, surface reconstruction and video compression. Sensors 2021, 22, 197. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Sun, S.; Yan, W.; Liu, G.; Li, X. A method based on curvature and hierarchical strategy for dynamic point cloud compression in augmented and virtual reality system. Sensors 2022, 22, 1262. [Google Scholar] [CrossRef] [PubMed]
- Thanou, D.; Chou, P.A.; Frossard, P. Graph-Based Compression of Dynamic 3D Point Cloud Sequences. IEEE Trans. Image Process. 2016, 25, 1765–1778. [Google Scholar] [CrossRef] [PubMed]
- Puang, E.Y.; Zhang, H.; Zhu, H.; Jing, W. Hierarchical Point Cloud Encoding and Decoding with Lightweight Self-Attention Based Model. IEEE Robot. Autom. Lett. 2022, 7, 4542–4549. [Google Scholar] [CrossRef]
- Tatarchenko, M.; Dosovitskiy, A.; Brox, T. Octree generating networks: Efficient convolutional architectures for high-resolution 3d outputs. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2088–2096. [Google Scholar]
- Dai, A.; Qi, C.R.; Nießner, M. Shape Completion Using 3D-Encoder-Predictor CNNs and Shape Synthesis. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6545–6554. [Google Scholar] [CrossRef]
- Luo, S.; Hu, W. Diffusion probabilistic models for 3d point cloud generation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 2837–2845. [Google Scholar]
- Yu, J.; Wang, J.; Sun, L.; Wu, M.E.; Zhu, Q. Point Cloud Geometry Compression Based on Multi-Layer Residual Structure. Entropy 2022, 24, 1677. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, L.; Tian, J.; Zhang, Y.; Fang, Z. Variable Rate Point Cloud Geometry Compression Method. Sensors 2023, 23, 5474. [Google Scholar] [CrossRef] [PubMed]
- You, K.; Gao, P. Patch-based deep autoencoder for point cloud geometry compression. arXiv 2021, arXiv:2110.09109. [Google Scholar]
- You, K.; Gao, P.; Li, Q. IPDAE: Improved Patch-Based Deep Autoencoder for Lossy Point Cloud Geometry Compression. In Proceedings of the 1st International Workshop on Advances in Point Cloud Compression, Processing and Analysis, Lisbon, Portugal, 14 October 2022; pp. 1–10. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5099–5108. [Google Scholar]
- Que, Z.; Lu, G.; Xu, D. Voxelcontext-net: An octree based framework for point cloud compression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 6042–6051. [Google Scholar]
- Biswas, S.; Liu, J.; Wong, K.; Wang, S.; Urtasun, R. Muscle: Multi sweep compression of lidar using deep entropy models. Adv. Neural Inf. Process. Syst. 2020, 33, 22170–22181. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the naacL-HLT, Minneapolis, MN, USA, 2 June 2019; Volume 1, p. 2. [Google Scholar]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I. Improving Language Understanding by Generative Pre-Training. Technical Report, OpenAI. 2018. Available online: https://openai.com/research/language-unsupervised (accessed on 15 October 2023).
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P.J. Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res. 2020, 21, 5485–5551. [Google Scholar]
- Parmar, N.; Vaswani, A.; Uszkoreit, J.; Kaiser, L.; Shazeer, N.; Ku, A.; Tran, D. Image transformer. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 4055–4064. [Google Scholar]
- Kolesnikov, A.; Dosovitskiy, A.; Weissenborn, D.; Heigold, G.; Uszkoreit, J.; Beyer, L.; Minderer, M.; Dehghani, M.; Houlsby, N.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Wu, X.; Lao, Y.; Jiang, L.; Liu, X.; Zhao, H. Point transformer v2: Grouped vector attention and partition-based pooling. Adv. Neural Inf. Process. Syst. 2022, 35, 33330–33342. [Google Scholar]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 16259–16268. [Google Scholar]
- Misra, I.; Girdhar, R.; Joulin, A. An end-to-end transformer model for 3d object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2906–2917. [Google Scholar]
- Sheng, H.; Cai, S.; Liu, Y.; Deng, B.; Huang, J.; Hua, X.S.; Zhao, M.J. Improving 3d object detection with channel-wise transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2743–2752. [Google Scholar]
- Wang, Y.; Ye, T.; Cao, L.; Huang, W.; Sun, F.; He, F.; Tao, D. Bridged transformer for vision and point cloud 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12114–12123. [Google Scholar]
- Gao, Y.; Liu, X.; Li, J.; Fang, Z.; Jiang, X.; Huq, K.M.S. LFT-Net: Local feature transformer network for point clouds analysis. IEEE Trans. Intell. Transp. Syst. 2022, 24, 2158–2168. [Google Scholar] [CrossRef]
- Park, C.; Jeong, Y.; Cho, M.; Park, J. Fast point transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16949–16958. [Google Scholar]
- Lai, X.; Liu, J.; Jiang, L.; Wang, L.; Zhao, H.; Liu, S.; Qi, X.; Jia, J. Stratified transformer for 3d point cloud segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8500–8509. [Google Scholar]
- Xu, S.; Wan, R.; Ye, M.; Zou, X.; Cao, T. Sparse cross-scale attention network for efficient lidar panoptic segmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, Palo Alto, CA, USA, 22 February–1 March 2022; Volume 36, pp. 2920–2928. [Google Scholar]
- Yu, W.; Luo, M.; Zhou, P.; Si, C.; Zhou, Y.; Wang, X.; Feng, J.; Yan, S. Metaformer is actually what you need for vision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10819–10829. [Google Scholar]
- Lee-Thorp, J.; Ainslie, J.; Eckstein, I.; Ontanon, S. FNet: Mixing Tokens with Fourier Transforms. In Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Seattle, WA, USA, 10–15 July 2022; pp. 4296–4313. [Google Scholar]
- Wang, W.; Xie, E.; Li, X.; Fan, D.P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pyramid vision transformer: A versatile backbone for dense prediction without convolutions. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 568–578. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–15 June 2015; pp. 1912–1920. [Google Scholar]
- D’Eon, E.; Harrison, B.; Myers, T.; Chou, P.A. 8i voxelized full bodies—A voxelized point cloud dataset. ISO/IEC JTC1/SC29 Jt. 2017, 7, 11. [Google Scholar]
- Xu, Y.; Lu, Y.; Wen, Z. Owlii Dynamic human mesh sequence dataset. In Proceedings of the ISO/IEC JTC1/SC29/WG11 m41658, 120th MPEG Meeting, Macau, 23–27 October 2017; Volume 1. [Google Scholar]
- Loop, C.; Cai, Q.; Escolano, S.O.; Chou, P.A. Microsoft voxelized upper bodies—A voxelized point cloud dataset. In Proceedings of the ISO/IEC JTC1/SC29 Joint WG11/WG1 (MPEG/JPEG) m38673/M72012, Geneva, Switzerland, 30 May–3 June 2016; Volume 1. [Google Scholar]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. Shapenet: An information-rich 3d model repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]





| Point Clouds | D1(p2point) | ||||||
|---|---|---|---|---|---|---|---|
| G-PCC(T) [20] | G-PCC(O) [20] | ADL-PCC [14] | GeoCNNv2 [6] | Learned-PCGC [7] | MRM-PCGC [33] | VA-PCC [34] | |
| Longderss_vox10 | −81.35 | −97.33 | −42.36 | −43.08 | −16.31 | −5.98 | −15.63 |
| Loot_vox10 | −79.47 | −96.96 | −40.42 | −39.5 | −14.9 | −5.74 | −15.06 |
| Red&black_vox10 | −80.71 | −92.04 | −29.52 | −44.58 | −17.26 | −1.68 | −10.46 |
| Soldier_vox10 | −80.62 | −95.48 | −39.4 | −43.42 | −41.21 | −5.11 | −13.47 |
| Queen_vox10 | −79.19 | −98.23 | −34.1 | −29.07 | −9.73 | - | - |
| Player_vox11 | −81.76 | −99.85 | −41.63 | −38.55 | −15.07 | - | −15.29 |
| Dancer_vox11 | −82.79 | −99.71 | −37.89 | −34.89 | −13.24 | - | −14.78 |
| Average | −80.84 | −97.09 | −37.9 | −39.01 | −14.39 | −4.63 | −14.12 |
| Point Clouds | D2(p2plane) | ||||||
|---|---|---|---|---|---|---|---|
| G-PCC(T) [20] | G-PCC(O) [20] | ADL-PCC [14] | GeoCNNv2 [6] | Learned-PCGC [7] | MRM-PCGC [33] | VA-PCC [34] | |
| Longderss_vox10 | −76.56 | −96.95 | −41.07 | −36.26 | −12.24 | −12.19 | −17.79 |
| Loot_vox10 | −74.84 | −96.41 | −39.5 | −32.37 | −13.53 | −11.22 | −16.37 |
| Red&black_vox10 | −75.28 | −94.24 | −30.47 | −33.16 | −13.17 | −9.21 | −14.99 |
| Soldier_vox10 | −75.97 | −95.25 | −37.8 | −36.57 | −12.95 | −10.51 | −15.82 |
| Queen_vox10 | −75.27 | −98.78 | −38.07 | −20.81 | −11.78 | - | - |
| Player_vox11 | −82.66 | −99.99 | −47.06 | −40.72 | −21.62 | - | −15.48 |
| Dancer_vox11 | −82.52 | −99.98 | −47.95 | −42.58 | −31.3 | - | −15.51 |
| Average | −77.59 | −97.37 | −40.27 | −34.64 | −16.66 | −10.78 | −15.99 |
| Point Clouds | G-PCC(O) [20] | Learned-PCGC [7] | ||
|---|---|---|---|---|
| D1 | D2 | D1 | D2 | |
| 8iVFB | −96 | −96.32 | −15.13 | −13.08 |
| Owlii | −78.03 | −75.55 | −13.45 | −29.4 |
| MVUB | −83.34 | −68.85 | −9.86 | −2.53 |
| ModelNet | - | - | −24.57 | −12.06 |
| ShapeNet | - | - | −28.27 | −12.1 |
| Average | −85.79 | −80.24 | −18.26 | −13.83 |
| G-PCC(O) [20] | G-PCC(T) [20] | Learned-PCGC [7] | Ours | |
|---|---|---|---|---|
| Encoding time | 1.6 | 8.16 | 6.63 | 7.42 |
| Decoding time | 0.6 | 6.58 | 17.49 | 12.85 |
| Model size | 2.6 M | 2.6 M | 8.0 M | 4.0 M |
| Ablation | Variant | Bpp | D1 | D2 |
|---|---|---|---|---|
| Baseline | [Trans, Trans, Trans] | 0.59 | 75.45 | 79.53 |
| Hybrid Stages | [Trans, Trans, Trans] → [Trans, Trans*2, Trans] | 0.58 | 75.48 | 79.57 |
| [Trans, Trans, Trans] → [Trans, Trans*3, Trans] | 0.59 | 75.45 | 79.53 | |
| Activation | GeLU → ReLU | 0.55 | 75.45 | 79.58 |
| GeLU → Swich | 0.55 | 74.53 | 78.58 | |
| Normalization | Group Normalization → Layer Normalization | 0.54 | 75.22 | 79.36 |
| Group Normalization→ Batch Normalization | 0.55 | 75.54 | 79.71 | |
| Token mixers | Pooling size 7→5 | 0.55 | 75.47 | 79.62 |
| Pooling size 7→9 | 0.55 | 75.46 | 79.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, S.; Yang, H.; Han, C. TransPCGC: Point Cloud Geometry Compression Based on Transformers. Algorithms 2023, 16, 484. https://doi.org/10.3390/a16100484
Lu S, Yang H, Han C. TransPCGC: Point Cloud Geometry Compression Based on Transformers. Algorithms. 2023; 16(10):484. https://doi.org/10.3390/a16100484
Chicago/Turabian StyleLu, Shiyu, Huamin Yang, and Cheng Han. 2023. "TransPCGC: Point Cloud Geometry Compression Based on Transformers" Algorithms 16, no. 10: 484. https://doi.org/10.3390/a16100484
APA StyleLu, S., Yang, H., & Han, C. (2023). TransPCGC: Point Cloud Geometry Compression Based on Transformers. Algorithms, 16(10), 484. https://doi.org/10.3390/a16100484