Trees Adjust the Shape of Branch Unions to Increase Their Load-Bearing Capacity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Destructive Pulling Tests
2.2. Morphological Analysis
2.3. Statistical Analysis
3. Results
3.1. Breaking Stress
3.2. Morphological Analyses
3.2.1. Leonardo’s Rule
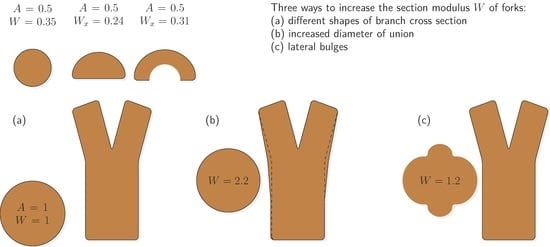
3.2.2. Section Modulus and Bending Stress
4. Discussion
- Increasing section modulus from the stem base up to where the stems part;
- An increase in the section modulus caused by lateral bulges;
- An increase in the section modulus of the branches caused by an optimized shape.
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wessolly, L.; Erb, M. Handbuch der Baumstatik und Baumkontrolle; Patzer: Berlin, Germany; Hannover, Germany, 2014; ISBN 978-3-87617-128-9. [Google Scholar]
- Mattheck, C.; Breloer, H. Handbuch der Schadenskunde von Bäumen; Rombach Wissenschaft: Baden-Baden, Germany, 1993; Volume 4. [Google Scholar]
- Koeser, A.K.; Smiley, E.T.; Hauer, R.J.; Kane, B.; Klein, R.W.; Landry, S.M.; Sherwood, M. Can Professionals Gauge Likelihood of Failure?—Insights from Tropical Storm Matthew. Urban For. Urban Green. 2020, 52, 126701. [Google Scholar] [CrossRef]
- Nelson, M.F.; Klein, R.W.; Koeser, A.K.; Landry, S.M.; Kane, B. The Impact of Visual Defects and Neighboring Trees on Wind-Related Tree Failures. Forests 2022, 13, 978. [Google Scholar] [CrossRef]
- Kane, B.; Finn, J.T. Factors Affecting Branch Failures in Open-Grown Trees during a Snowstorm in Massachusetts, USA. SpringerPlus 2014, 3, 720. [Google Scholar] [CrossRef] [PubMed]
- Gibbs, J.N.; Greig, B.J.W. Survey of Parkland Trees after the Great Storm of October 16, 1987. Arboric. J. 1990, 14, 321–347. [Google Scholar] [CrossRef]
- Mattheck, C.; Vorberg, U. The Biomechanics of Tree Fork Design. Bot. Acta 1991, 104, 399–404. [Google Scholar] [CrossRef]
- Wäldchen, M. Die Beurteilung von Zwieseln. AFZ-Der Wald 2007, 61, 406–407. [Google Scholar]
- Wessolly, L.; Erb, M. Manual of Tree Statics and Tree Inspection; Patzer Verlag: Berlin, Germany; Hannover, Germany, 2016; ISBN 978-3-87617-143-2. [Google Scholar]
- Mattheck, C. Aktualisierte Feldanleitung Für Baumkontrollen; Forschungszentrum Karlsruhe GmbH: Karlsruhe, Germany, 2007. [Google Scholar]
- Slater, D. The Mechanical Effects of Bulges Developed around Bark-Included Branch Junctions of Hazel (Corylus avellana L.) and Other Trees. Trees 2021, 35, 513–526. [Google Scholar] [CrossRef]
- Dunster, J.A.; Smiley, E.T.; Matheny, N.; Lilly, S. Tree Risk Assessment Manual; International Society of Arboriculture: Champaign, IL, USA, 2013. [Google Scholar]
- Kane, B.; Farrell, R.; Zedaker, S.M.; Loferski, J.R.; Smith, D.W. Failure Mode and Prediction of the Strength of Branch Attachments. Arboric. Urban For. 2008, 34, 308–316. [Google Scholar] [CrossRef]
- Sinn, T. Handbuch Baumstatik: Schadsymptome und Messverfahren zur Feststellung der Stand- und Bruchsicherheit; Quelle & Meyer Verlag: Wiebelsheim, Germany, 2022; ISBN 978-3-494-01922-2. [Google Scholar]
- Lilly, S.; Sydnor, T. Comparison of Branch Failure during Static Loading of Silver and Norway Maples. J. Arboric. 1995, 21, 302–305. [Google Scholar] [CrossRef]
- Gilman, E.F. Branch-to-Stem Diameter Ratio Affects Strength of Attachment. J. Arboric. 2003, 29, 291–293. [Google Scholar] [CrossRef]
- Pfisterer, J.A.; Spatz, H.C.; Erforth, D.; Heinz, M. Untersuchungen zur Biegebruchfestigkeit von Astgabeln und Reiteraten der Hasel (Corylus avellana L.). In Proceedings of the Deutsche Baumpflegetage, Augsburg, Germany, 22–24 April 2003; pp. 158–235. [Google Scholar]
- Smiley, E.T. Does Included Bark Reduce the Strength of Codominant Stems? J. Arboric. 2003, 29, 104–106. [Google Scholar] [CrossRef]
- Slater, D.; Ennos, R. Interlocking Wood Grain Patterns Provide Improved Wood Strength Properties in Forks of Hazel (Corylus avellana L.). Arboric. J. 2015, 37, 21–32. [Google Scholar] [CrossRef]
- Walkden, E. Modelling the Strength of the Branch Attachments. Arboric. J. 2016, 38, 109–119. [Google Scholar] [CrossRef]
- Rathjens, R.; Sydnor, T.D.; Grabosky, J.; Dahle, G. Structural Pruning in Callery Pear Does Not Change Apparent Branch Union Strength in Seventh Year Static Load Field Testing. AUF 2021, 47, 123–130. [Google Scholar] [CrossRef]
- Dahle, G.A.; Eckenrode, R.T.; Smiley, E.T.; DeVallance, D.; Holásková, I. Can Mechanical Strain and Aspect Ratio Be Used to Determine Codominant Unions in Red Maple without Included Bark. Forests 2022, 13, 1007. [Google Scholar] [CrossRef]
- Zimmermann, M.H. Xylem Structure and the Ascent of Sap; Springer Series in Wood Science; Springer: Berlin/Heidelberg, Germanyy, 1983; ISBN 978-3-662-22629-2. [Google Scholar]
- Tyree, M.T.; Ewers, F.W. The Hydraulic Architecture of Trees and Other Woody Plants. N. Phytol. 1991, 119, 345–360. [Google Scholar] [CrossRef]
- Shinozaki, K.; Yoda, K.; Hozumi, K.; Kira, T. A Quantitative Analysis of Plant Form—The Pipe Model Theorie I. Basic Analyses. Jpn. J. Ecol. 1964, 14, 97–104. [Google Scholar]
- Nikinmaa, E. Analyses of the Growth of Scots Pine; Matching Structure with Function. Acta For. Fenn. 1992, 235, 68p. [Google Scholar] [CrossRef]
- Shinozaki, K.; Yoda, K.; Hozumi, K.; Kira, T. A Quantitative Analysis of Plant Form—The Pipe Model Theorie II. Further Evidence of the Theory and Its Application in Forest Ecology. Jpn. J. Ecol. 1964, 14, 133–139. [Google Scholar]
- Metzger, C. Der Wind als maßgebender Faktor für das Wachsthum der Bäume. Mündener Forstl. Hefte 1893, 3, 35–86. [Google Scholar]
- Ylinen, A. Über die Mechanische Schaftformtheorie der Bäume; Silva Fennica; Technische Hochschule in Finnland: Helsinki, Finnland, 1952; p. 50. [Google Scholar]
- Büsgen, M.; Münch, E. Bau und Leben unserer Waldbäume; Fischer: Jena, Germany, 1927. [Google Scholar]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 Years of Image Analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- CloudCompare—Open Source Project. Available online: www.cloudcompare.org (accessed on 15 April 2023).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Niklas, K.J.; Spatz, H.-C. Plant Physics; The University of Chicago Press: Chicago, IL, USA; London, UK, 2012; ISBN 978-0-226-58632-8. [Google Scholar]
- Oppelt, A.L.; Kurth, W.; Godbold, D.L. Topology, Scaling Relations and Leonardo’s Rule in Root Systems from African Tree Species. Tree Physiol. 2001, 21, 117–128. [Google Scholar] [CrossRef] [PubMed]
- Sone, K.; Suzuki, A.A.; Miyazawa, S.-I.; Noguchi, K.; Terashima, I. Maintenance Mechanisms of the Pipe Model Relationship and Leonardo Da Vinci’s Rule in the Branching Architecture of Acer Rufinerve Trees. J. Plant Res. 2009, 122, 41–52. [Google Scholar] [CrossRef] [PubMed]
- Eloy, C. Leonardo’s Rule, Self-Similarity, and Wind-Induced Stresses in Trees. Phys. Rev. Lett. 2011, 107, 258101. [Google Scholar] [CrossRef]
- Sotolongo-Costa, O.; Villasana-Mercado, P.; Sánchez-Calderón, L.; Rodríguez-Vargas, I. Statistical Hydraulic Model for the Leonardo’s Rule. arXiv 2020, arXiv:2009.10310. [Google Scholar] [CrossRef]
- Minamino, R.; Tateno, M. Tree Branching: Leonardo Da Vinci’s Rule versus Biomechanical Models. PLoS ONE 2014, 9, e93535. [Google Scholar] [CrossRef]
- Jaffe, M.J.; Forbes, S. Thigmomorphogenesis: The Effect of Mechanical Perturbation on Plants. Plant Growth Regul. 1993, 12, 313–324. [Google Scholar] [CrossRef]
- Tateno, M. Increase in Lodging Safety Factor of Thigmomorphogenically Dwarfed Shoots of Mulberry Tree. Physiol. Plant. 1991, 81, 239–243. [Google Scholar] [CrossRef]
- Telewski, F.W.; Pruyn, M.L. Thigmomorphogenesis: A Dose Response to Flexing in Ulmus Americana Seedlings. Tree Physiol. 1998, 18, 65–68. [Google Scholar] [CrossRef]
- Slater, D.; Ennos, R. An Assessment of the Remodeling of Bifurcations in Hazel (Corylus avellana L.) in Response to Bracing, Drilling, and Splitting. Arboric. Urban For. 2016, 42, 355–370. [Google Scholar] [CrossRef]
- Slater, D.; Ennos, A.R. Determining the Mechanical Properties of Hazel Forks by Testing Their Component Parts. Trees 2013, 27, 1515–1524. [Google Scholar] [CrossRef]
- Arseniou, G.; MacFarlane, D.W.; Calders, K.; Baker, M. Accuracy Differences in Aboveground Woody Biomass Estimation with Terrestrial Laser Scanning for Trees in Urban and Rural Forests and Different Leaf Conditions. Trees 2023, 37, 761–779. [Google Scholar] [CrossRef]
- Guo, Y.; Luka, A.; Wei, Y. Modeling Urban Tree Growth for Digital Twins: Transformation of Point Clouds into Parametric Crown Models. J. Digit. Landsc. Archit. 2022, 30, 213–223. [Google Scholar] [CrossRef]
- Arseniou, G.; MacFarlane, D.W.; Seidel, D. Measuring the Contribution of Leaves to the Structural Complexity of Urban Tree Crowns with Terrestrial Laser Scanning. Remote Sens. 2021, 13, 2773. [Google Scholar] [CrossRef]
- Kükenbrink, D.; Gardi, O.; Morsdorf, F.; Thürig, E.; Schellenberger, A.; Mathys, L. Above-Ground Biomass References for Urban Trees from Terrestrial Laser Scanning Data. Ann. Bot. 2021, 128, 709–724. [Google Scholar] [CrossRef] [PubMed]
- Blackman, R.; Yuan, F. Detecting Long-Term Urban Forest Cover Change and Impacts of Natural Disasters Using High-Resolution Aerial Images and LIDAR Data. Remote Sens. 2020, 12, 1820. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.Y.; Sanesi, G.; Lafortezza, R. Remote Sensing in Urban Forestry: Recent Applications and Future Directions. Remote Sens. 2019, 11, 1144. [Google Scholar] [CrossRef]







| Species | Shape: U/V | Diameter Ratio | Bifurcation Angle | Included Bark |
|---|---|---|---|---|
| Sycamore maple 1 | - | - | - | - |
| Red Maple | * | * | - | * |
| Silver Maple | - | |||
| Norway maple | - | |||
| European beech 1 | - | - | - | - |
| Hazelnut | * | - | * | |
| Pedunculate oak | * | |||
| Sawtooth oak | * | * | * | * |
| Callery pear | */- | * |
| Species | Shape | n | Basal Diameter, cm |
|---|---|---|---|
| A. pseudoplatanus | U | 5 | 20.1–34.4 |
| V | 8 | 18.1–29.0 | |
| F. sylvatica | U | 22 | 18.1–44.9 |
| V | 58 | 16.6–52.5 |
| Species | n | Basal Diameter, cm |
|---|---|---|
| Fagus sylvatica | 33 | 12.7–116.2 |
| Acer pseudoplatanus | 25 | 30.9–89.1 |
| Fraxinus excelsior | 21 | 4.9–96.7 |
| Acer campestre | 19 | 19.8–44.4 |
| Tilia cordata | 17 | 29.5–78.8 |
| Prunus avium | 6 | 31.8–63.9 |
| Quercus robur | 2 | 75.2–114.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rust, S. Trees Adjust the Shape of Branch Unions to Increase Their Load-Bearing Capacity. Forests 2023, 14, 1041. https://doi.org/10.3390/f14051041
Rust S. Trees Adjust the Shape of Branch Unions to Increase Their Load-Bearing Capacity. Forests. 2023; 14(5):1041. https://doi.org/10.3390/f14051041
Chicago/Turabian StyleRust, Steffen. 2023. "Trees Adjust the Shape of Branch Unions to Increase Their Load-Bearing Capacity" Forests 14, no. 5: 1041. https://doi.org/10.3390/f14051041
APA StyleRust, S. (2023). Trees Adjust the Shape of Branch Unions to Increase Their Load-Bearing Capacity. Forests, 14(5), 1041. https://doi.org/10.3390/f14051041