Hydraulic Constraints to Whole-Tree Water Use and Respiration in Young Cryptomeria Trees under Competition
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plant Material and Study Site
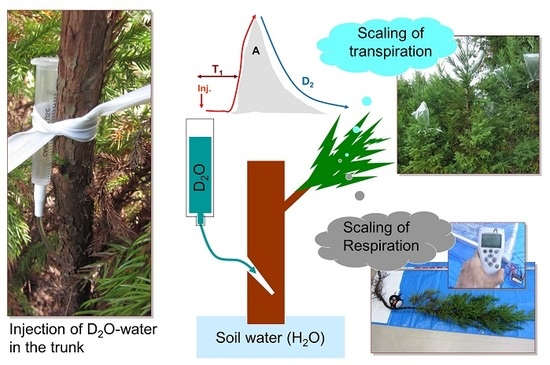
2.2. Quantification of Water Transport and Storage through Deuterium-Dilution Method
2.3. Isotope Analyses
2.4. Measurement of Respiration Rates and Biometric Variables
2.5. Data Analysis
3. Results
3.1. Tree Morphometric Variables
3.2. Respiration Rates and Their Association with Tree Size
3.3. Water Use and Water Storage
3.4. Association between Hydraulic, Metabolic, and Morphometric Traits
4. Discussion
4.1. Biomass Allocation Patterns Differ in Dominant and Suppressed Trees
4.2. Metabolic Rates Tend to Compensate for Changes in Biomass Allocation
4.3. Transpiration Rates Show a Negative Allometric Response to Tree Size
4.4. Hydraulic Limitations in Suppressed Trees May Reduce Their Water-Use Efficiency
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B

| Organ | Model | R2 | a | b (95% c.i.) 1 | p-Value |
|---|---|---|---|---|---|
| Roots FW | y = axb | 0.77 | 2.03 | 0.51(0.39 0.63) | <0.001 |
| Stem FW | 0.78 | 1.78 | 0.43(0.33 0.52) | <0.001 | |
| Leaves FW | 0.84 | 1.40 | 0.55(0.45 0.65) | <0.001 | |
| Shoot FW | y = axb | 0.83 | 1.12 | 0.51(0.41 0.61) | <0.001 |
| Total FW | 0.82 | 0.97 | 0.51(0.41 0.62) | <0.001 |
References
- Camarero, J.J.; Gazol, A.; Tardif, J.C.; Conciatori, F. Attributing forest responses to global-change drivers: Limited evidence of a CO2-fertilization effect in Iberian pine growth. J. Biogeogr. 2015, 42, 2220–2233. [Google Scholar] [CrossRef]
- Franklin, J.; Serra-Diaz, J.M.; Syphard, A.D.; Regan, H.M. Global change and terrestrial plant community dynamics. Proc. Natl. Acad. Sci. USA 2016, 113, 3725–3734. [Google Scholar] [CrossRef] [PubMed]
- Girardin, M.P.; Bouriaud, O.; Hogg, E.H.; Kurz, W.; Zimmermann, N.E.; Metsaranta, J.M.; de Jong, R.; Frank, D.C.; Esper, J.; Büntgen, U.; et al. No growth stimulation of Canada’s boreal forest under half-century of combined warming and CO2 fertilization. Proc. Natl. Acad. Sci. USA 2016, 113, E8406–E8414. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Zhang, C.; Wang, Q.; Chen, X.; Ding, J.; Karamage, F. Isolating and Quantifying the Effects of Climate and CO2 Changes (1980–2014) on the Net Primary Productivity in Arid and Semiarid China. Forests 2017, 8, 60. [Google Scholar] [CrossRef]
- Shestakova, T.A.; Camarero, J.J.; Ferrio, J.P.; Knorre, A.A.; Gutiérrez, E.; Voltas, J. Increasing drought effects on five European pines modulate Δ13C-growth coupling along a Mediterranean altitudinal gradient. Funct. Ecol. 2017, 31, 1359–1370. [Google Scholar] [CrossRef]
- Shestakova, T.A.; Voltas, J.; Saurer, M.; Siegwolf, R.T.W.; Kirdyanov, A.V. Warming effects on Pinus sylvestris in the cold-dry Siberian forest-steppe: Positive or negative balance of trade? Forests 2017, 8. [Google Scholar] [CrossRef]
- Pšidová, E.; Živčák, M.; Stojnić, S.; Orlović, S.; Gömöry, D.; Kučerová, J.; Ditmarová, L.; Střelcová, K.; Brestič, M.; Kalaji, H.M. Altitude of origin influences the responses of PSII photochemistry to heat waves in European beech (Fagus sylvatica L.). Environ. Exp. Bot. 2017, 152, 97–106. [Google Scholar] [CrossRef]
- Jaramillo, F.; Cory, N.; Arheimer, B.; Laudon, H.; Van Der Velde, Y.; Hasper, T.B.; Teutschbein, C.; Uddling, J. Dominant effect of increasing forest biomass on evapotranspiration: Interpretations of movement in Budyko space. Hydrol. Earth Syst. Sci. 2018, 22, 567–580. [Google Scholar] [CrossRef]
- Mulder, C.; Boit, A.; Mori, S.; Vonk, J.A.; Dyer, S.D.; Faggiano, L.; Geisen, S.; González, A.L.; Kaspari, M.; Lavorel, S.; et al. Distributional (In)Congruence of Biodiversity-Ecosystem Functioning; Academic Press: Cambridge, MA, USA, 2012; Volume 46. [Google Scholar]
- Meng, S.; Jia, Q.; Zhou, G.; Zhou, H.; Liu, Q.; Yu, J. Fine root biomass and its relationship with aboveground traits of Larix gmelinii trees in Northeastern China. Forests 2018, 9, 1–11. [Google Scholar] [CrossRef]
- Ruehr, N.K.; Offermann, C.A.; Gessler, A.; Winkler, J.B.; Ferrio, J.P.; Buchmann, N.; Barnard, R.L. Drought effects on allocation of recent carbon: From beech leaves to soil CO2 efflux. New Phytol. 2009, 184, 950–961. [Google Scholar] [CrossRef] [PubMed]
- Hasibeder, R.; Fuchslueger, L.; Richter, A.; Bahn, M. Summer drought alters carbon allocation to roots and root respiration in mountain grassland. New Phytol. 2015, 205, 1117–1127. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Montes, E.; Tomás, M.; Medrano, H.; Escalona, J.M. Effect of soil water availability on root respiration in grapevines—Importance for plant carbon balance. In Acta Horticulturae; International Society for Horticultural Science (ISHS): Leuven, Belgium, 2016; pp. 103–108. [Google Scholar]
- Teodosio, B.; Pauwels, V.R.N.; Loheide, S.P., II; Daly, E. Relationship between root water uptake and soil respiration: a modeling perspective. J. Geophys. Res. Biogeosci. 2017, 122, 1954–1968. [Google Scholar] [CrossRef]
- Pausch, J.; Kuzyakov, Y. Carbon input by roots into the soil: Quantification of rhizodeposition from root to ecosystem scale. Glob. Chang. Biol. 2018, 24, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Andrews, M.; Raven, J.A.; Sprent, J.I. Environmental effects on dry matter partitioning between shoot and root of crop plant: relations with growth and shoot protein concentration. Ann. Appl. Biol. 2001, 138, 57–68. [Google Scholar] [CrossRef]
- Ledo, A.; Paul, K.I.; Burslem, D.F.R.P.; Ewel, J.J.; Barton, C.; Battaglia, M.; Brooksbank, K.; Carter, J.; Eid, T.H.; England, J.R.; et al. Tree size and climatic water deficit control root to shoot ratio in individual trees globally. New Phytol. 2018, 217, 8–11. [Google Scholar] [CrossRef] [PubMed]
- Hommel, R.; Siegwolf, R.; Saurer, M.; Farquhar, G.D.; Kayler, Z.; Ferrio, J.P.; Gessler, A. Drought response of mesophyll conductance in forest understory species—Impacts on water-use efficiency and interactions with leaf water movement. Physiol. Plant. 2014, 152, 98–114. [Google Scholar] [CrossRef] [PubMed]
- Martín-Gómez, P.; Aguilera, M.; Pemán, J.; Gil-Pelegrín, E.; Ferrio, J.P. Contrasting ecophysiological strategies related to drought: the case of a mixed stand of Scots pine (Pinus sylvestris) and a submediterranean oak (Quercus subpyrenaica). Tree Physiol. 2017, 37, 1478–1492. [Google Scholar] [CrossRef] [PubMed]
- Iwasa, Y.; Roughgarden, J. Shoot/Root balance of plants: optimal growth of a system with many vegetative organs. Theor. Popul. Biol. 1984, 105, 78–105. [Google Scholar] [CrossRef]
- Bloom, A.J.; Chapin, F.S.; Mooney, H.A. Resource Limitation in Plants—An Economic Analogy. Annu. Rev. Ecol. Syst. 1985, 16, 363–392. [Google Scholar] [CrossRef]
- Fardusi, M.J.; Ferrio, J.P.; Comas, C.; Voltas, J.; Resco de Dios, V.; Serrano, L. Intra-specific association between carbon isotope composition and productivity in woody plants: A meta-analysis. Plant Sci. 2016, 251, 110–118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lopez Caceres, M.L.; Nakano, S.; Ferrio, J.P.; Hayashi, M.; Nakatsuka, T.; Sano, M.; Yamanaka, T.; Nobori, Y. Evaluation of the effect of the 2011 Tsunami on coastal forests by means of multiple isotopic analyses of tree-rings. Isotopes Environ. Health Stud. 2018, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Canham, C.D.; Berkowitz, A.R.; Kelly, V.R.; Lovett, G.M.; Ollinger, S.V; Schnurr, J. Biomass allocation and multiple resource limitation in tree seedlings. Can. J. For. Res. Can. Rech. For. 1996, 26, 1521–1530. [Google Scholar] [CrossRef]
- Coll, L.; Balandier, P.; Picon-Cochard, C.; Prévosto, B.; Curt, T. Competition for water between beech seedlings and surrounding vegetation in different light and vegetation composition conditions. Ann. For. Sci. 2003, 60, 593–600. [Google Scholar] [CrossRef] [Green Version]
- Yamashita, K.; Mizoue, N.; Ito, S.; Inoue, A.; Kaga, H. Effects of residual trees on tree height of 18- and 19-year-old Cryptomeria japonica planted in group selection openings. J. For. Res. 2006, 11, 227–234. [Google Scholar] [CrossRef]
- Nagakura, J.; Shigenaga, H.; Akama, A.; Takahashi, M. Growth and transpiration of Japanese cedar (Cryptomeria japonica) and Hinoki cypress (Chamaecyparis obtusa) seedlings in response to soil water content. Tree Physiol. 2004, 24, 1203–1208. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Zeng, F.; Peng, W.; Wang, K.; Zhang, H.; Liu, L.; Song, T. Carbon storage in a Eucalyptus plantation chronosequence in Southern China. Forests 2015, 6, 1763–1778. [Google Scholar] [CrossRef]
- Zavala, M.A.; Bravo De La Parra, R. A mechanistic model of tree competition and facilitation for Mediterranean forests: Scaling from leaf physiology to stand dynamics. Ecol. Modell. 2005, 188, 76–92. [Google Scholar] [CrossRef]
- Mori, S.; Yamaji, K.; Ishida, A.; Prokushkin, S.G.; Masyagina, O.V.; Hagihara, A.; Hoque, A.T.M.R.; Suwa, R.; Osawa, A.; Nishizono, T.; et al. Mixed-power scaling of whole-plant respiration from seedlings to giant trees. Proc. Natl. Acad. Sci. USA 2010, 107, 1447–1451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gargallo-Garriga, A.; Sardans, J.; Pérez-Trujillo, M.; Rivas-Ubach, A.; Oravec, M.; Vecerova, K.; Urban, O.; Jentsch, A.; Kreyling, J.; Beierkuhnlein, C.; et al. Opposite metabolic responses of shoots and roots to drought. Sci. Rep. 2014, 4, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Kleiber, M. Body size and metabolism. Hilgardia A J. Agric. Sci. 1932, 6, 315–353. [Google Scholar] [CrossRef] [Green Version]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef] [PubMed]
- DeLong, J.P.; Okie, J.G.; Moses, M.E.; Sibly, R.M.; Brown, J.H. Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc. Natl. Acad. Sci. USA 2010, 107, 12941–12945. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glazier, D. Body-Mass Scaling of Metabolic Rate: What are the Relative Roles of Cellular versus Systemic Effects? Biology (Basel) 2015, 4, 187–199. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hedin, L.O. Physiology: Plants on a different scale. Nature 2006, 439, 399–400. [Google Scholar] [CrossRef] [PubMed]
- Hosoda, K.; Iehara, T. Aboveground biomass equations for individual trees of Cryptomeria japonica, Chamaecyparis obtusa and Larix kaempferi in Japan. J. For. Res. 2010, 15, 299–306. [Google Scholar] [CrossRef]
- Nishizono, T.; Kitahara, F.; Iehara, T.; Mitsuda, Y. Geographical variation in age-height relationships for dominant trees in Japanese cedar (Cryptomeria japonica D. Don) forests in Japan. J. For. Res. 2014, 19, 305–316. [Google Scholar] [CrossRef]
- Ishii, H. How do changes in leaf/shoot morphology and crown architecture affect growth and physiological function of tall trees? Tree Physiol. 2011, 4, 215–232. [Google Scholar] [CrossRef]
- Azuma, W.; Ishii, H.R.; Kuroda, K.; Kuroda, K. Function and structure of leaves contributing to increasing water storage with height in the tallest Cryptomeria japonica trees of Japan. Trees 2016, 30, 141–152. [Google Scholar] [CrossRef]
- Azuma, W.; Nakashima, S.; Yamakita, E.; Ishii, H.R.; Kuroda, K. Water retained in tall Cryptomeria japonica leaves as studied by infrared micro-spectroscopy. Tree Physiol. 2017, 37, 1367–1378. [Google Scholar] [CrossRef] [PubMed]
- Himeno, S.; Azuma, W.; Gyokusen, K.; Ishii, H.R. Leaf water maintains daytime transpiration in young Cryptomeria japonica trees. Tree Physiol. 2017, 37, 1394–1403. [Google Scholar] [CrossRef] [PubMed]
- Calder, I.R.; Kariyappa, G.S.; Srinivasalu, N.V.; Srinivasa Murty, K.V. Deuterium tracing for the estimation of transpiration from trees Part 1. Field calibration. J. Hydrol. 1992, 130, 17–25. [Google Scholar] [CrossRef]
- Meinzer, F.C.; James, S.A.; Goldstein, G. Dynamics of transpiration, sap flow and use of stored water in tropical forest canopy trees. Tree Physiol. 2004, 24, 901–909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Calder, I.R.; Swaminath, M.H.; Kariyappa, G.S.; Srinivasalu, N.V.; Srinivasa Murty, K.V.; Mumtaz, J. Deuterium tracing for the estimation of transpiration from trees Part 3. Measurements of transpiration from Eucalyptus plantation, India. J. Hydrol. 1992, 130, 37–48. [Google Scholar] [CrossRef]
- Schwendenmann, L.; Dierick, D.; Köhler, M.; Hölscher, D. Can deuterium tracing be used for reliably estimating water use of tropical trees and bamboo? Tree Physiol. 2010, 30, 886–900. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meinzer, F.C.; Brooks, J.R.; Domec, J.C.; Gartner, B.L.; Warren, J.M.; Woodruff, D.R.; Bible, K.; Shaw, D.C. Dynamics of water transport and storage in conifers studied with deuterium and heat tracing techniques. Plant Cell Environ. 2006, 29, 105–114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Inoue, S.; Shirota, T.; Mitsuda, Y.; Ishii, H.; Gyokusen, K. Effects of individual size, local competition and canopy closure on the stem volume growth in a monoclonal Japanese cedar (Cryptomeria japonica D. Don) plantation. Ecol. Res. 2008, 23, 953–964. [Google Scholar] [CrossRef]
- Lim, H.; Lee, K.H.; Lee, K.H.; Park, I.H. Biomass expansion factors and allometric equations in an age sequence for Japanese cedar (Cryptomeria japonica) in southern Korea. J. For. Res. 2013, 18, 316–322. [Google Scholar] [CrossRef]
- Genet, M.; Kokutse, N.; Stokes, A.; Fourcaud, T.; Cai, X.; Ji, J.; Mickovski, S. Root reinforcement in plantations of Cryptomeria japonica D. Don: Effect of tree age and stand structure on slope stability. For. Ecol. Manage. 2008, 256, 1517–1526. [Google Scholar] [CrossRef]
- Klein, T.; Randin, C.; Körner, C. Water availability predicts forest canopy height at the global scale. Ecol. Lett. 2015, 18, 1311–1320. [Google Scholar] [CrossRef] [PubMed]
- Reich, P.B.; Tjoelker, M.G.; Machado, J.L.; Oleksyn, J. Universal scaling of respiratory metabolism, size and nitrogen in plants. Nature 2006, 439, 457–461. [Google Scholar] [CrossRef] [PubMed]
- Makita, N.; Kosugi, Y.; Dannoura, M.; Takanashi, S.; Niiyama, K.; Kassim, A.R.; Nik, A.R. Patterns of root respiration rates and morphological traits in 13 tree species in a tropical forest. Tree Physiol. 2012, 32, 303–312. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bentley, L.P.; Stegen, J.C.; Savage, V.M.; Smith, D.D.; von Allmen, E.I.; Sperry, J.S.; Reich, P.B.; Enquist, B.J. An empirical assessment of tree branching networks and implications for plant allometric scaling models. Ecol. Lett. 2013, 16, 1069–1078. [Google Scholar] [CrossRef] [PubMed]
- Kodama, N.; Barnard, R.; Salmon, Y.; Weston, C.; Ferrio, J.P.; Holst, J.; Werner, R.; Saurer, M.; Buchmann, N.; Rennenberg, H.; et al. Temporal dynamics of the carbon isotope composition in a Pinus sylvestris stand—From newly assimilated organic carbon to respired CO2. Oecologia 2008, 156, 737–750. [Google Scholar] [CrossRef] [PubMed]
- Gessler, A.; Tcherkez, G.; Karyanto, O.; Keitel, C.; Ferrio, J.P.; Ghashghaie, J.; Kreuzwieser, J.; Farquhar, G.D. On the metabolic origin of the carbon isotope composition of CO2 evolved from darkened light-acclimated leaves in Ricinus communis. New Phytol. 2009, 181, 374–386. [Google Scholar] [CrossRef] [PubMed]
- Kumagai, T.; Aoki, S.; Otsuki, K.; Utsumi, Y. Impact of stem water storage on diurnal estimates of whole-tree transpiration and canopy conductance from sap flow measurements in Japanese cedar and Japanese cypress trees. Hydrol. Process. 2009, 23, 2335–2344. [Google Scholar] [CrossRef]
- Meinzer, F.C.; Bond, B.J.; Warren, J.M.; Woodruff, D.R. Does water transport scale universally with tree size? Funct. Ecol. 2005, 19, 558–565. [Google Scholar] [CrossRef] [Green Version]
- Santiago, G.; Meinzer, J.B.; Machado, K.; Woodruff, D.; Jones, T.L.S.; Goldstein, F.C.F. Leaf photosynthetic traits scale with hydraulic conductivity and wood density in Panamian forest canopy trees. Ecophysiology 2004, 140, 543–550. [Google Scholar]
- Chave, J.; Coomes, D.; Jansen, S.; Lewis, S.L.; Swenson, N.G.; Zanne, A.E. Towards a worldwide wood economics spectrum. Ecol. Lett. 2009, 12, 351–366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoeber, S.; Leuschner, C.; Köhler, L.; Arias-Aguilar, D.; Schuldt, B. The importance of hydraulic conductivity and wood density to growth performance in eight tree species from a tropical semi-dry climate. For. Ecol. Manag. 2014, 330, 126–136. [Google Scholar] [CrossRef]








| Variable 1 | Mean ± S.E. | Range | Median |
|---|---|---|---|
| Tree Height (m) | 1.60 ± 0.122 | [0.75 2.81] | 1.50 |
| Basal Area (BA, mm2) | 494 ± 84.6 | [112 1605] | 413 |
| BAI-3y (mm2 year−1) | 102 ± 20.8 | [12 391] | 74 |
| Stem volume (cm3) | 372 ± 85.4 | [29 1673] | 231 |
| Root FW (kg) | 0.39 ± 0.091 | [0.05 2.18] | 0.23 |
| Stem FW (kg) | 0.46 ± 0.110 | [0.04 2.28] | 0.26 |
| Leaf FW (kg) | 0.81 ± 0.166 | [0.11 3.52] | 0.53 |
| Shoot FW (kg) | 1.27 ± 0.275 | [0.16 5.80] | 0.81 |
| Total FW (kg) | 1.66 ± 0.364 | [0.21 7.98] | 1.03 |
| Variable 1 | Mean ± S.E. | Range | Median |
|---|---|---|---|
| Time for peak maximum (days) | 1.1 ± 0.04 | [0.93 1.95] | 1.09 |
| D/H atom % peak | 0.203 ± 0.0282 | [0.037 0.614] | 0.142 |
| D/H atom % last sampling | 0.016 ± 0.0002 | [0.015 0.020] | 0.016 |
| Tracer velocity (Vel, cm day−1) | 8.6 ± 2.12 | [1.7 53.0] | 4.3 |
| Water use (WU, g day–1) | 943 ± 173.1 | [195 3415] | 649 |
| Leaf-specific WU (g day-1 kg−1) | 1298 ± 65.9 | [949 2431] | 1212 |
| Half life (t½, days) | 0.9 ± 0.09 | [0.4 2.3] | 0.8 |
| Residence time (RT, days) | 2.8 ± 0.21 | [1.3 5.1] | 2.7 |
| X-Variable 1 | Organ | Model | R2 | a | b (95% c.i.) 2 | p-Value |
|---|---|---|---|---|---|---|
| WU | Roots | y = 10axb | 0.85 | −3.83 | 0.942(0.77 1.12) | <0.001 |
| Stem | 0.93 | −4.44 | 1.183(1.04 1.33) | <0.001 | ||
| Leaves | 0.92 | −3.62 | 1.040(0.90 1.18) | <0.001 | ||
| Vel | Roots | y = 10axb | 0.40 | −1.63 | 0.622(0.30 0.95) | <0.001 |
| Stem | 0.36 | −1.63 | 0.707(0.30 1.12) | 0.001 | ||
| Leaves | 0.42 | −1.20 | 0.680(0.34 1.03) | <0.001 | ||
| WC | Roots | Log(y) = a + bx | 0.36 | −5.01 | 6.671(2.79 10.55) | 0.002 |
| Stem | 0.61 | −7.38 | 11.85(7.76 15.93) | <0.001 | ||
| Leaves | 0.01 | −1.79 | 1.705(−5.25 +8.66) | 0.6167 | ||
| Stem density | Roots | Log(y) = a + (b/100)x | 0.26 | 0.43 | −0.247(−0.43 −0.06) | 0.009 |
| Stem | 0.32 | 1.00 | −0.326(−0.53 −0.12) | 0.004 | ||
| Leaves | 0.41 | 1.44 | −0.330(−0.50 −0.16) | <0.001 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrio, J.P.; Kurosawa, Y.; Wang, M.; Mori, S. Hydraulic Constraints to Whole-Tree Water Use and Respiration in Young Cryptomeria Trees under Competition. Forests 2018, 9, 449. https://doi.org/10.3390/f9080449
Ferrio JP, Kurosawa Y, Wang M, Mori S. Hydraulic Constraints to Whole-Tree Water Use and Respiration in Young Cryptomeria Trees under Competition. Forests. 2018; 9(8):449. https://doi.org/10.3390/f9080449
Chicago/Turabian StyleFerrio, Juan Pedro, Yoko Kurosawa, Mofei Wang, and Shigeta Mori. 2018. "Hydraulic Constraints to Whole-Tree Water Use and Respiration in Young Cryptomeria Trees under Competition" Forests 9, no. 8: 449. https://doi.org/10.3390/f9080449
APA StyleFerrio, J. P., Kurosawa, Y., Wang, M., & Mori, S. (2018). Hydraulic Constraints to Whole-Tree Water Use and Respiration in Young Cryptomeria Trees under Competition. Forests, 9(8), 449. https://doi.org/10.3390/f9080449