Validation of Model-Based Melt Viscosity in Hot-Melt Extrusion Numerical Simulation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Methods
2.2.1. Helium Pycnometry
2.2.2. Differential Scanning Calorimetry (DSC)
2.2.3. Solubility Determination via DSC
2.2.4. Small Amplitude Oscillatory Shear (SAOS) Measurements
2.2.5. Procedure to Generate the Model-Based Melt Viscosity
2.2.6. Computation of Extrusion Experiments by Using the Software Ludovic®
2.2.7. Hot-Melt Extrusion Experiments
3. Results
3.1. API Solubility in the Polymeric Matrix and The Deviation from Couchman-Karasz Fit
3.2. Evaluation of Potential Physical Property Changes
3.3. Comparison of SAOS Measurements and Model-Based Melt Viscosity Calculation
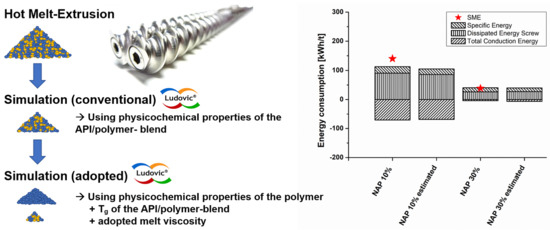
3.4. Energy Consumption in HME Experiments, Conventional Simulation, and Simulation Using Model-Based Melt Viscosity
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- LaFountaine, J.S.; McGinity, J.W.; Williams, R.O. Challenges and strategies in thermal processing of amorphous solid dispersions: A review. AAPS PharmSciTech 2016, 17, 43–55. [Google Scholar] [CrossRef] [PubMed]
- Patil, H.; Tiwari, R.V.; Repka, M.A. Hot-melt extrusion: From theory to application in pharmaceutical formulation. AAPS PharmSciTech 2016, 17, 20–42. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, R.V.; Patil, H.; Repka, M.A. Contribution of hot-melt extrusion technology to advance drug delivery in the 21st century. Expert Opin. Drug Deliv. 2016, 13, 451–464. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.M.; Dudhedia, M.S.; Zimny, E. Hot melt extrusion: Development of an amorphous solid dispersion for an insoluble drug from mini-scale to clinical scale. AAPS PharmSciTech 2016, 17, 133–147. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Su, Y.; Zhang, J.; DiNunzio, J.; Leone, A.; Huang, C.; Brown, C.D. Rheology guided rational selection of processing temperature to prepare copovidone–nifedipine amorphous solid dispersions via hot melt extrusion (HME). Mol. Pharm. 2016, 13, 3494–3505. [Google Scholar] [CrossRef] [PubMed]
- Chan, S.-Y.; Qi, S.; Craig, D.Q.M. An investigation into the influence of drug–polymer interactions on the miscibility, processability and structure of polyvinylpyrrolidone-based hot melt extrusion formulations. Int. J. Pharm. 2015, 496, 95–106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zecevic, D.E.; Wagner, K.G. Rational Development of solid dispersions via hot-melt extrusion using screening, material characterization, and numeric simulation tools. J. Pharm. Sci. 2013, 102, 2297–2310. [Google Scholar] [CrossRef] [PubMed]
- Thiry, J.; Krier, F.; Evrard, B. A review of pharmaceutical extrusion: Critical process parameters and scaling-up. Int. J. Pharm. 2015, 479, 227–240. [Google Scholar] [CrossRef] [PubMed]
- Zecevic, D.E.; Evans, R.C.; Paulsen, K.; Wagner, K.G. From benchtop to pilot scale-experimental study and computational assessment of a hot-melt extrusion scale-up of a solid dispersion of dipyridamole and copovidone. Int. J. Pharm. 2018, 537, 132–139. [Google Scholar] [CrossRef] [PubMed]
- Grimard, J.; Dewasme, L.; Vande Wouwer, A. A review of dynamic models of hot-melt extrusion. Processes 2016, 4, 19. [Google Scholar] [CrossRef]
- Rantanen, J.; Khinast, J. The future of pharmaceutical manufacturing sciences. J. Pharm. Sci. 2015, 104, 3612–3638. [Google Scholar] [CrossRef] [PubMed]
- Gaspar-Cunha, A.; Poulesquen, A.; Vergnes, B.; Covas, J.A. Optimization of processing conditions for polymer twin-screw extrusion. Int. Polym. Process. 2002, 17, 201–213. [Google Scholar] [CrossRef]
- Durin, A.; De Micheli, P.; Nguyen, H.C.; David, C.; Valette, R.; Vergnes, B. Comparison between 1D and 3D approaches for twin-screw extrusion simulation. Int. Polym. Process. 2014, 29, 641–648. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Covas, J.A.; Vergnes, B. Defining the configuration of co-rotating twin-screw extruders with multiobjective evolutionary algorithms. Polym. Eng. Sci. 2005, 45, 1159–1173. [Google Scholar] [CrossRef]
- Sarhangi Fard, A.S.; Anderson, P.D. Simulation of distributive mixing inside mixing elements of co-rotating twin-screw extruders. Comput. Fluids 2013, 87, 79–91. [Google Scholar] [CrossRef]
- Lozano, T.; Lafleur, P.G.; Grmela, M.; Vergnes, B. Modeling filler dispersion along a twin-screw extruder. Int. Polym. Process. 2003, 18, 12–19. [Google Scholar] [CrossRef]
- Malik, M.; Kalyon, D.M.; Golba, J.C. Jr. Simulation of co-rotating twin screw extrusion process subject to pressure-dependent wall slip at barrel and screw surfaces: 3D FEM analysis for combinations of forward-and reverse-conveying screw elements. Int. Polym. Process. 2014, 29, 51–62. [Google Scholar] [CrossRef]
- Zhang, X.M.; Feng, L.F.; Hoppe, S.; Hu, G.H. Local residence time, residence revolution, and residence volume distributions in twin-screw extruders. Polym. Eng. Sci. 2008, 48, 19–28. [Google Scholar] [CrossRef]
- Gao, J.; Walsh, G.C.; Bigio, D.; Briber, R.M.; Wetzel, M.D. Residence-time distribution model for twin-screw extruders. AIChE J. 1999, 45, 2541–2549. [Google Scholar] [CrossRef]
- Bochmann, E.S.; Üstüner, E.E.; Gryczke, A.; Wagner, K.G. Predicting melt rheology for hot-melt extrusion by means of a simple Tg-measurement. Eur. J. Pharm. Biopharm. 2017, 119, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Bochmann, E.S.; Steffens, K.E.; Gryczke, A.; Wagner, K.G. Numerical simulation of hot-melt extrusion processes for amorphous solid dispersions using model-based melt viscosity. Eur. J. Pharm. Biopharm. 2018, 124, 34–42. [Google Scholar] [CrossRef] [PubMed]
- Bochmann, E.S.; Neumann, D.; Gryczke, A.; Wagner, K.G. Micro-scale prediction method for API-solubility in polymeric matrices and process model for forming amorphous solid dispersion by hot-melt extrusion. Eur. J. Pharm. Biopharm. 2016, 107, 40–48. [Google Scholar] [CrossRef] [PubMed]
- Prudic, A.; Ji, Y.; Sadowski, G. Thermodynamic phase behavior of API/polymer solid dispersions. Mol. Pharm. 2014, 11, 2294–2304. [Google Scholar] [CrossRef] [PubMed]
- Marsac, P.J.; Shamblin, S.L.; Taylor, L.S. Theoretical and practical approaches for prediction of drug–polymer miscibility and solubility. Pharm. Res. 2006, 23, 2417–2426. [Google Scholar] [CrossRef] [PubMed]
- Mahieu, A.; Willart, J.F.; Dudognon, E.; Danède, F.; Descamps, M. A new protocol to determine the solubility of drugs into polymer matrixes. Mol. Pharm. 2013, 10, 560–566. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Thiessen, P.A.; Bolton, E.E.; Chen, J.; Fu, G.; Gindulyte, A.; Han, L.; He, J.; He, S.; Shoemaker, B.A.; et al. PubChem substance and compound databases. Nucleic Acids Res. 2016, 44, D1202–D1213. [Google Scholar] [CrossRef] [PubMed]
- Brostow, W.; Chiu, R.; Kalogeras, I.M.; Vassilikou-Dova, A. Prediction of glass transition temperatures: Binary blends and copolymers. Mater. Lett. 2008, 62, 3152–3155. [Google Scholar] [CrossRef]
- Couchman, P.R.; Karasz, F.E. A classical thermodynamic discussion of the effect of composition on glass-transition temperatures. Macromol. 1978, 11, 117–119. [Google Scholar] [CrossRef]
- Carreau, P.J. Rheological equations from molecular network theories. Trans. Soc. Rheol. 1972, 16, 99–127. [Google Scholar] [CrossRef]
- Yasuda, K. Investigation of the Analogies between Viscometric and Linear Viscoelastic Properties of Polystyrene Fluids. Ph.D. thesis, Massachusetts Inst. of Technology, Cambridge, MA, USA, May 1979. [Google Scholar]
- Doolittle, A.K. Studies in Newtonian flow. II. The dependence of the viscosity of liquids on free-space. J. Appl. Phys. 1951, 22, 1471–1475. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Vergnes, B.; Valle, G.D.; Delamare, L. A global computer software for polymer flows in corotating twin screw extruders. Polym. Eng. Sci. 1998, 38, 1781–1792. [Google Scholar] [CrossRef]
- Teixeira, C.; Gaspar-Cunha, A.; Covas, J.A. Flow and heat transfer along the length of a co-rotating twin screw extruder. Polym. Plast. Technol. Eng. 2012, 51, 1567–1577. [Google Scholar] [CrossRef]
- Carneiro, O.S.; Covas, J.A.; Vergnes, B. Experimental and theoretical study of twin-screw extrusion of polypropylene. J. Appl. Polym. Sci. 2000, 78, 1419–1430. [Google Scholar] [CrossRef]
- Baird, J.A.; Taylor, L.S. Evaluation of amorphous solid dispersion properties using thermal analysis techniques. Adv. Drug Deliv. Rev. 2012, 64, 396–421. [Google Scholar] [CrossRef] [PubMed]
- Kohlgrüber, K.; Bierdel, M. Co-Rotating Twin-Screw Extruders: Fundamentals, Technology, and Applications, 1st ed.; Carl Hanser Publishers: Munich, Germany; Hanser Gardner Publications: Cincinnati, OH, USA, 2008; pp. 72–74. ISBN 978-1-56990-422-0. [Google Scholar]


 ), Couchman–Karasz (CK) and Brostow Chiu Kalogeras Vassilikou-Dova (BCKV) fits of celecoxib (a), loratadine (b), naproxen (c), and praziquantel (d) in different weight fractions in copovidone.
), Couchman–Karasz (CK) and Brostow Chiu Kalogeras Vassilikou-Dova (BCKV) fits of celecoxib (a), loratadine (b), naproxen (c), and praziquantel (d) in different weight fractions in copovidone.
 ), Couchman–Karasz (CK) and Brostow Chiu Kalogeras Vassilikou-Dova (BCKV) fits of celecoxib (a), loratadine (b), naproxen (c), and praziquantel (d) in different weight fractions in copovidone.
), Couchman–Karasz (CK) and Brostow Chiu Kalogeras Vassilikou-Dova (BCKV) fits of celecoxib (a), loratadine (b), naproxen (c), and praziquantel (d) in different weight fractions in copovidone.


| Substance | Molecular Weight (g/mol) | Melting Point (°C) | Glass Transition Temperature (°C) | Heat Capacity Step at Tg (J/g·K) |
|---|---|---|---|---|
| Celecoxib (CXB) | 381.4 | 160.9 | 56.8 | 0.39 |
| Loratadine (LOR) | 382.9 | 134.6 | 34.9 | 0.30 |
| Naproxen (NAP) | 230.3 | 156.1 | 6.7 1 | 0.23 |
| Praziquantel (PZQ) | 312.4 | 138.3 | 35.9 | 0.37 |
| Copovidone (COP) | 45,000–70,000 | - | 107 | 0.40 |
| Mixture | Tg (°C) | ρ (kg/m3) Powder | ρ (kg/m3) Extrudate | Cp (J/(g·K)) at 25 °C | Cp (J/(g·K)) at 150 °C |
|---|---|---|---|---|---|
| COP | 107 | 1178 | 1191 | 1.013 | 1.720 |
| CXB 10% | 104 | 1230 | 1208 | 1.142 | 1.819 |
| CXB 30% | 101 | 1279 | 1237 | 1.011 | 1.878 |
| LOR 10% | 96 | 1215 | 1202 | 1.143 | 2.003 |
| LOR 30% | 75 | 1200 | 1204 | 1.097 | 1.864 |
| NAP 10% | 92 | 1190 | 1202 | 1.182 | 1.963 |
| NAP 30% | 71 | 1217 | 1209 | 1.117 | 1.883 |
| PZQ 10% | 96 | 1220 | 1200 | 1.165 | 1.899 |
| PZQ 30% | 72 | 1200 | 1209 | 1.104 | 1.862 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bochmann, E.S.; Gryczke, A.; Wagner, K.G. Validation of Model-Based Melt Viscosity in Hot-Melt Extrusion Numerical Simulation. Pharmaceutics 2018, 10, 132. https://doi.org/10.3390/pharmaceutics10030132
Bochmann ES, Gryczke A, Wagner KG. Validation of Model-Based Melt Viscosity in Hot-Melt Extrusion Numerical Simulation. Pharmaceutics. 2018; 10(3):132. https://doi.org/10.3390/pharmaceutics10030132
Chicago/Turabian StyleBochmann, Esther S., Andreas Gryczke, and Karl G. Wagner. 2018. "Validation of Model-Based Melt Viscosity in Hot-Melt Extrusion Numerical Simulation" Pharmaceutics 10, no. 3: 132. https://doi.org/10.3390/pharmaceutics10030132
APA StyleBochmann, E. S., Gryczke, A., & Wagner, K. G. (2018). Validation of Model-Based Melt Viscosity in Hot-Melt Extrusion Numerical Simulation. Pharmaceutics, 10(3), 132. https://doi.org/10.3390/pharmaceutics10030132