The Role of Cocrystallization-Mediated Altered Crystallographic Properties on the Tabletability of Rivaroxaban and Malonic Acid
Abstract
:1. Introduction
2. Materials
3. Methods
3.1. Crystallization Experiments
3.1.1. RIV for Compaction Study
3.1.2. MAL for Compaction Study
3.1.3. RIV-MAL Co for Compaction Study
3.2. Differential Scanning Calorimetry (DSC)
3.3. X-Ray Powder Diffractometry (XRPD)
3.4. Particle Size Distribution (PSD)
3.5. Specific Surface Area (SSA) Measurement
3.6. Moisture Content (MC)
3.7. True Density Determination
3.8. Preparation of Compacts for Studying Bulk Deformation Behavior
3.9. Calculation of Tensile Strength and Porosity
3.10. Nanoindentation Experimentation
3.11. Molecular Modeling
3.12. Attachment Energy Calculations
3.13. Statistical Analysis
4. Results and Discussion
4.1. Solid-State Characterization
4.2. Particle Level and Bulk Level Attributes
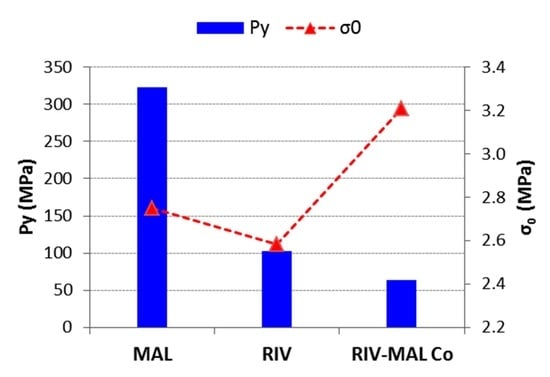
4.3. Bulk Deformation Behaviour
4.3.1. Heckel Analysis
4.3.2. Ryshkewitch‒Duckworth Analysis
4.4. Particle Level Deformation: Quantifying Crystal Deformation by Nanoindentation
4.5. Identification of Crystallographic Features
4.5.1. Crystallographic Features of RIV-MAL Co
4.5.2. Crystallographic Features of RIV
4.5.3. Crystallographic Features of MAL
4.6. Decoding the Basis of Bulk Deformation Behavior: Impact of Crystallographic and Supramolecular Features
4.6.1. Impact of Crystallographic Features on Plasticity
4.6.2. Impact of Crystallographic Features on BS
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shelley, C.F. Chapter 12. Oral delivery of immediate release dosage form. In Remington Education: Pharmaceutics; Pharmaceutical Press: London, UK, 2014; pp. 287–313. [Google Scholar]
- Schultheiss, N.; Newman, A. Pharmaceutical cocrystals and their physicochemical properties. Cryst. Growth Des. 2009, 9, 2950–2967. [Google Scholar] [CrossRef] [Green Version]
- Desiraju, G.R.; Vittal, J.J.; Ramanan, A. Crystal engineering: A textbook; World Scientific Publishing Co.: Toh Tuck, Singapore, 2011. [Google Scholar]
- Bolla, G.; Nangia, A. Pharmaceutical cocrystals: Walking the talk. Chem. Commun. 2016, 52, 8342–8360. [Google Scholar] [CrossRef] [PubMed]
- Kale, D.P.; Zode, S.S.; Bansal, A.K. Challenges in translational development of pharmaceutical cocrystals. J. Pharm. Sci. 2017, 106, 457–470. [Google Scholar] [CrossRef] [PubMed]
- Good, D.J.; Rodríguez-Hornedo, N.r. Solubility advantage of pharmaceutical cocrystals. Cryst. Growth Des. 2009, 9, 2252–2264. [Google Scholar] [CrossRef]
- Yoshimura, M.; Miyake, M.; Kawato, T.; Bando, M.; Toda, M.; Kato, Y.; Fukami, T.; Ozeki, T. Impact of the dissolution profile of the cilostazol cocrystal with supersaturation on the oral bioavailability. Cryst. Growth Des. 2017, 17, 550–557. [Google Scholar] [CrossRef]
- Jasani, M.S.; Kale, D.P.; Singh, I.P.; Bansal, A.K. Influence of drug–polymer interactions on dissolution of thermodynamically highly unstable cocrystal. Mol. Pharm. 2018, 16, 151–164. [Google Scholar] [CrossRef]
- Trask, A.V.; Motherwell, W.D.S.; Jones, W. Physical stability enhancement of theophylline via cocrystallization. Int. J. Pharm. 2006, 320, 114–123. [Google Scholar] [CrossRef]
- Kale, D.P.; Ugale, B.; Nagaraja, C.; Dubey, G.; Bharatam, P.V.; Bansal, A.K. Molecular basis of water sorption behavior of rivaroxaban-malonic acid cocrystal. Mol. Pharm. 2019, 16, 2980–2991. [Google Scholar] [CrossRef]
- Shinozaki, T.; Ono, M.; Higashi, K.; Moribe, K. A novel drug-drug cocrystal of levofloxacin and metacetamol: Reduced hygroscopicity and improved photostability of levofloxacin. J. Pharm. Sci. 2019, 108, 2383–2390. [Google Scholar] [CrossRef]
- Yadav, J.P.; Yadav, R.N.; Uniyal, P.; Chen, H.; Wang, C.; Sun, C.C.; Kumar, N.; Bansal, A.K.; Jain, S. Molecular interpretation of mechanical behavior in four basic crystal packing of Isoniazid with homologous cocrystal formers. Crystal Growth & Design 2020, 20, 832–844. [Google Scholar]
- Reddy, C.M.; Krishna, G.R.; Ghosh, S. Mechanical properties of molecular crystals—applications to crystal engineering. CrystEngComm 2010, 12, 2296–2314. [Google Scholar] [CrossRef]
- Karki, S.; Frisic, T.; Fabian, L.; Laity, P.R.; Day, G.M.; Jones, W. Improving mechanical properties of crystalline solids by cocrystal formation: New compressible forms of paracetamol. Adv. Mater. 2009, 21, 3905–3909. [Google Scholar] [CrossRef]
- Krishna, G.R.; Shi, L.; Bag, P.P.; Sun, C.C.; Reddy, C.M. Correlation among crystal structure, mechanical behavior, and tabletability in the co-crystals of vanillin isomers. Cryst. Growth Des. 2015, 15, 1827–1832. [Google Scholar] [CrossRef]
- Aher, S.; Dhumal, R.; Mahadik, K.; Ketolainen, J.; Paradkar, A. Effect of cocrystallization techniques on compressional properties of caffeine/oxalic acid 2: 1 cocrystal. Pharm. Dev. Technol. 2013, 18, 55–60. [Google Scholar] [CrossRef]
- Hiendrawan, S.; Veriansyah, B.; Widjojokusumo, E.; Soewandhi, S.N.; Wikarsa, S.; Tjandrawinata, R.R. Physicochemical and mechanical properties of paracetamol cocrystal with 5-nitroisophthalic acid. Int. J. Pharm. 2016, 497, 106–113. [Google Scholar] [CrossRef]
- Pedersen, S.; Kristensen, H. Compaction behaviour of 4-hydroxybenzoic acid and two esters compared to their mechanical properties. Eur. J. Pharm. Biopharm. 1995, 41, 323–328. [Google Scholar]
- Khomane, K.S.; More, P.K.; Raghavendra, G.; Bansal, A.K. Molecular understanding of the compaction behavior of indomethacin polymorphs. Mol. Pharm. 2013, 10, 631–639. [Google Scholar] [CrossRef]
- Picker-Freyer, K.M.; Liao, X.; Zhang, G.; Wiedmann, T.S. Evaluation of the compaction of sulfathiazole polymorphs. J. Pharm. Sci. 2007, 96, 2111–2124. [Google Scholar] [CrossRef]
- Sun, C.C. Decoding powder tabletability: Roles of particle adhesion and plasticity. J. Adhes. Sci. Technol. 2011, 25, 483–499. [Google Scholar] [CrossRef]
- Osei-Yeboah, F.; Chang, S.-Y.; Sun, C.C. A critical examination of the phenomenon of bonding area-bonding strength interplay in powder tableting. Pharm. Res. 2016, 33, 1126–1132. [Google Scholar] [CrossRef]
- Joiris, E.; Di Martino, P.; Berneron, C.; Guyot-Hermann, A.-M.; Guyot, J.-C. Compression behavior of orthorhombic paracetamol. Pharm. Res. 1998, 15, 1122–1130. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.C.; Hou, H. Improving mechanical properties of caffeine and methyl gallate crystals by cocrystallization. Cryst. Growth Des. 2008, 8, 1575–1579. [Google Scholar] [CrossRef] [Green Version]
- Khomane, K.S.; More, P.K.; Bansal, A.K. Counterintuitive compaction behavior of clopidogrel bisulfate polymorphs. J. Pharm. Sci. 2012, 101, 2408–2416. [Google Scholar] [CrossRef] [PubMed]
- Upadhyay, P.; Khomane, K.S.; Kumar, L.; Bansal, A.K. Relationship between crystal structure and mechanical properties of ranitidine hydrochloride polymorphs. CrystEngComm 2013, 15, 3959–3964. [Google Scholar] [CrossRef]
- Egart, M.; Janković, B.; Srčič, S. Application of instrumented nanoindentation in preformulation studies of pharmaceutical active ingredients and excipients. Acta Pharmaceutica 2016, 66, 303–330. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.; Morganti, M.; Hancock, B.C.; Masterson, V.M. Correlating particle hardness with powder compaction performance. J. Pharm. Sci. 2010, 99, 4307–4316. [Google Scholar] [CrossRef]
- Varughese, S.; Kiran, M.; Ramamurty, U.; Desiraju, G.R. Nanoindentation in crystal engineering: Quantifying mechanical properties of molecular crystals. Angew. Chem. Int. Ed. 2013, 52, 2701–2712. [Google Scholar] [CrossRef]
- Jing, Y.; Zhang, Y.; Blendell, J.; Koslowski, M.; Carvajal, M.T. Nanoindentation method to study slip planes in molecular crystals in a systematic manner. Cryst. Growth Des. 2011, 11, 5260–5267. [Google Scholar] [CrossRef]
- Duncan-Hewitt, W.C.; Weatherly, G.C. Evaluating the hardness, Young’s modulus and fracture toughness of some pharmaceutical crystals using microindentation techniques. J. Mater. Sci. Lett. 1989, 8, 1350–1352. [Google Scholar] [CrossRef]
- Yadav, J.P.; Yadav, R.N.; Sihota, P.; Chen, H.; Wang, C.; Sun, C.C.; Kumar, N.; Bansal, A.; Jain, S. Single-crystal plasticity defies bulk-phase mechanics in isoniazid cocrystals with analogous coformers. Cryst. Growth Des. 2019, 19, 4465–4475. [Google Scholar] [CrossRef]
- Persson, A.-S.; Ahmed, H.; Velaga, S.; Alderborn, G. Powder compression properties of paracetamol, paracetamol hydrochloride, and paracetamol cocrystals and coformers. J. Pharm. Sci. 2018, 107, 1920–1927. [Google Scholar] [CrossRef] [PubMed]
- Phadke, C.; Sharma, J.; Sharma, K.; Bansal, A.K. Effect of variability of physical properties of povidone K30 on crystallization and drug–polymer miscibility of celecoxib–povidone K30 amorphous solid dispersions. Mol. Pharm. 2019, 16, 4139–4148. [Google Scholar] [CrossRef] [PubMed]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Berkovitch-Yellin, Z. Toward an ab initio derivation of crystal morphology. J. Am. Chem. Soc. 1985, 107, 8239–8253. [Google Scholar] [CrossRef]
- Docherty, R.; Clydesdale, G.; Roberts, K.; Bennema, P. Application of Bravais-Friedel-Donnay-Harker, attachment energy and Ising models to predicting and understanding the morphology of molecular crystals. J. Phys. D: Appl. Phys. 1991, 24, 89. [Google Scholar] [CrossRef]
- Caires, F.J.; Lima, L.; Carvalho, C.; Giagio, R.; Ionashiro, M. Thermal behaviour of malonic acid, sodium malonate and its compounds with some bivalent transition metal ions. Thermochim. Acta 2010, 497, 35–40. [Google Scholar] [CrossRef]
- Khomane, K.S.; Bansal, A.K. Weak hydrogen bonding interactions influence slip system activity and compaction behavior of pharmaceutical powders. Journal of pharmaceutical sciences 2013, 102, 4242–4245. [Google Scholar] [CrossRef]
- Sun, C.C.; Grant, D.J. Improved tableting properties of p-hydroxybenzoic acid by water of crystallization: A molecular insight. Pharm. Res. 2004, 21, 382–386. [Google Scholar] [CrossRef]
- Sun, C.; Himmelspach, M.W. Reduced tabletability of roller compacted granules as a result of granule size enlargement. Journal of Parmaceutical Sciences 2006, 95, 200–206. [Google Scholar] [CrossRef]
- Khomane, K.S.; Bansal, A.K. Differential compaction behaviour of roller compacted granules of clopidogrel bisulphate polymorphs. Int. J. Pharm. 2014, 472, 288–295. [Google Scholar] [CrossRef]
- Patel, S.; Kaushal, A.M.; Bansal, A.K. Compression physics in the formulation development of tablets. Critical Reviews™ in Therapeutic Drug Carrier Systems 2006, 23, 1–66. [Google Scholar] [CrossRef] [PubMed]
- Heckel, R. Density-pressure relationships in powder compaction. Trans. Metall. Soc. AIME 1961, 221, 671–675. [Google Scholar]
- Ryshkewitch, E. Compression strength of porous sintered alumina and zirconia: 9th communication to ceramography. J. Am. Ceram. Soc. 1953, 36, 65–68. [Google Scholar] [CrossRef]
- Govedarica, B.; Ilić, I.; Šibanc, R.; Dreu, R.; Srčič, S. The use of single particle mechanical properties for predicting the compressibility of pharmaceutical materials. Powder Technol. 2012, 225, 43–51. [Google Scholar] [CrossRef]
- Roberts, R.; Rowe, R.; York, P. The relationship between indentation hardness of organic solids and their molecular structure. Journal of materials science 1994, 29, 2289–2296. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Grant, D.J. Plasticity and slip system of plate-shaped crystals of L-lysine monohydrochloride dihydrate. Pharm. Res. 2002, 19, 491–496. [Google Scholar] [CrossRef]
- Shariare, M.H.; Leusen, F.J.; de Matas, M.; York, P.; Anwar, J. Prediction of the mechanical behaviour of crystalline solids. Pharm. Res. 2012, 29, 319–331. [Google Scholar] [CrossRef]
- Sun, C.C.; Kiang, Y.H. On the identification of slip planes in organic crystals based on attachment energy calculation. J. Pharm. Sci. 2008, 97, 3456–3461. [Google Scholar] [CrossRef] [PubMed]
- Bryant, M.; Maloney, A.; Sykes, R. Predicting mechanical properties of crystalline materials through topological analysis. CrystEngComm 2018, 20, 2698–2704. [Google Scholar] [CrossRef]
- Ragnarsson, G.; Sjögren, J. Compressibility and tablet properties of two polymorphs of metoprolol tartrate. Acta Pharm. Suec. 1984, 21, 321–330. [Google Scholar]











| Material | PSD (µm) | SSA (m2/g) | MC (% w/w) | True Density (g/cm3) | |||
|---|---|---|---|---|---|---|---|
| D10 | D50 | D90 | Experimental | Crystallographic | |||
| MAL | 8.3 | 14.2 | 37.8 | 0.78 (0.09) | 0.264 (0.013) | 1.628 (0.001) | 1.621 |
| RIV | 7.1 | 10.2 | 31.5 | 0.85 (0.04) | 0.235 (0.014) | 1.536 (0.005) | 1.554 |
| RIV-MAL Co | 7.8 | 11.9 | 35.2 | 0.83 (0.07) | 0.242 (0.012) | 1.534 (0.007) | 1.548 |
| Sample | H (GPa) a | E (GPa) a | 1/E |
|---|---|---|---|
| RIV | 0.20 (0.02) | 3.41 (0.24) | 0.293 |
| MAL | 0.71 (0.08) | 17.91 (2.35) | 0.056 |
| RIV-MAL Co | 0.51 (0.04) | 17.58 (0.42) | 0.057 |
| Materials | CCDC Code | Slip Planes Identification by | Nanoindentation (Is Slip System Present?) | |
|---|---|---|---|---|
| Visualization | Attachment Energy (hkl), Eatt in kcal/mol $ | |||
| RIV-MAL Co | 1854618 | (0 0 1) | (0 0 1), −28.4 | present |
| RIV | 1854617 | (0 1 1) (1 0 2) | (0 1 1), −44.2 (0 0 1), −39.9 (1 0 2), −83.3 | present |
| MAL | 1209218 | absent | (1 0 0), −13.3 | absent |
| Materials | H-Bonding Dimensionality | No. of Slip Planes | d-Spacing (Å) and Slip Plane | Surface Topology |
|---|---|---|---|---|
| RIV-MAL Co | 1D | 1 | 6.2127, (0 0 1) * | Flat layers |
| RIV | 1D | 2 | 4.4850, (0 1 1) | Flat layers |
| 3.8752, (1 0 2) | Corrugated/Zigzag layers | |||
| MAL | 3D | 0 | - | Network of hydrogen bonds |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kale, D.P.; Puri, V.; Kumar, A.; Kumar, N.; Bansal, A.K. The Role of Cocrystallization-Mediated Altered Crystallographic Properties on the Tabletability of Rivaroxaban and Malonic Acid. Pharmaceutics 2020, 12, 546. https://doi.org/10.3390/pharmaceutics12060546
Kale DP, Puri V, Kumar A, Kumar N, Bansal AK. The Role of Cocrystallization-Mediated Altered Crystallographic Properties on the Tabletability of Rivaroxaban and Malonic Acid. Pharmaceutics. 2020; 12(6):546. https://doi.org/10.3390/pharmaceutics12060546
Chicago/Turabian StyleKale, Dnyaneshwar P., Vibha Puri, Amit Kumar, Navin Kumar, and Arvind K. Bansal. 2020. "The Role of Cocrystallization-Mediated Altered Crystallographic Properties on the Tabletability of Rivaroxaban and Malonic Acid" Pharmaceutics 12, no. 6: 546. https://doi.org/10.3390/pharmaceutics12060546
APA StyleKale, D. P., Puri, V., Kumar, A., Kumar, N., & Bansal, A. K. (2020). The Role of Cocrystallization-Mediated Altered Crystallographic Properties on the Tabletability of Rivaroxaban and Malonic Acid. Pharmaceutics, 12(6), 546. https://doi.org/10.3390/pharmaceutics12060546