Development and Application of a Mechanistic Cooling and Freezing Model of the Spin Freezing Step within the Framework of Continuous Freeze-Drying
Abstract
:1. Introduction
2. Materials and Methods
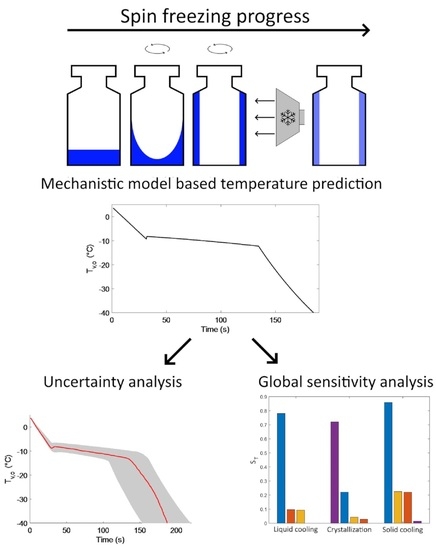
2.1. Spin Freezing
2.2. Mechanistic Cooling and Freezing Model
2.3. Uncertainty Analysis and Global Sensitivity Analysis
2.4. Experimental Model Verification of Constant Gas Flow Rate and Imposed Cooling Profile Experiments
3. Results and Discussion
3.1. Experimentally Obtained Vial Temperature Profiles and Subsequent Uncertainty Analysis
3.2. Imposed Cooling Profile
3.3. Global Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Glass transition temperature of the maximum freeze-concentrated drug solution (K) | |
| Eutectic temperature (K) | |
| Density of the solution (kg/m3) | |
| Specific heat capacity of the solution (J/(kg K)) (Nakagawa et al.) | |
| k | Thermal conductivity (W/(m K)) (Nakagawa et al.) |
| T | Temperature distribution of the system (K) (Nakagawa et al.) |
| Total latent heat released due to ice nucleation (W) (Nakagawa et al.) | |
| Total latent heat released due to ice crystallisation (W) (Nakagawa et al.) | |
| Latent heat of crystallization (J/kg) (Nakagawa et al.) | |
| Nucleation rate (kg/(m3 s K)) (Nakagawa et al.) | |
| Temperature in the supercooled liquid (K) (Nakagawa et al.) | |
| Freezing front velocity (m/s) (Nakagawa et al.) | |
| s | Thickness of the undercooled zone (m) (Nakagawa et al.) |
| Homogeneous undercooled temperature (K) (Nakagawa et al.) | |
| Fraction of ice suspended in the undercooled solution (Nakagawa et al.) | |
| Mean ice crystal size (m) | |
| a | an empirical constant based on experimental data (ms/K) in Equation (6) |
| R | Freezing front rate (m/s) |
| G | Temperature gradient in the frozen zone (K/m) |
| Thermocouple lag error (K) | |
| Time constant (s) | |
| Time constant regression model coefficient (1/s) | |
| Time constant regression model coefficient (ms) | |
| w | Velocity of the air flow (m/s) |
| Total heat released due to crystallization of ice (J) | |
| Mean rate of heat transfer (W) | |
| Mass of water in the vial (kg) | |
| h | Heat transfer coefficient (W/(mK)) |
| Diameter of the glass vial (m) | |
| Height of the glass vial (m) | |
| Temperature at the outside of the glass vial wall (K) | |
| Temperature of the gas (K) |
| Rate of heat transfer (W) | |
| Duration of the crystal growth phase (s) | |
| Volumetric gas flow (m/s) | |
| Regression coeffient (J/(mK)) | |
| Regression error term (W/(mK)) | |
| Total heat capacity of the system before freezing (J/K) | |
| Length of the modelling time step (s) | |
| Specific heat capacity of water (J/(kg K)) | |
| Specific heat capacity of the vial glass (J/(kg K)) | |
| Mass of the glass vial (kg) | |
| Radius of the nucleation ice crystal formation (m) | |
| The outer vial radius (m) | |
| Thermal conductivity of the vial glass (W/(m K)) | |
| Temperature at the inside of the glass vial wall (K) | |
| Thickness of the ice layer (m) | |
| Inner vial radius (m) | |
| Thermal conductivity of ice (W/(m K)) | |
| Equilibrium freezing temperature (K) | |
| Fraction of ice crystallized after nucleation | |
| Total heat capacity of the volume below the equilibrium freezing temperature (J/K) | |
| Nucleation temperature (K) | |
| Volume below the equilibrium freezing temperature (m) | |
| Density of water (kg/m) | |
| Density of ice (kg/m) | |
| Total heat capacity of the system after freezing (J/K) | |
| Specific heat capacity of ice (J/(kg K)) | |
| Mass of ice (kg) | |
| GSA | Global sensitivity analysis |
| UA | Uncertainty analysis |
| Total order effect | |
| Cooling rate (K/s) |
References
- De Meyer, L.; Van Bockstal, P.J.; Corver, J.; Vervaet, C.; Remon, J.P.; De Beer, T. Evaluation of spin freezing versus conventional freezing as part of a continuous pharmaceutical freeze-drying concept for unit doses. Int. J. Pharm. 2015, 496, 75–85. [Google Scholar] [CrossRef] [Green Version]
- Kasper, J.C.; Friess, W. The freezing step in lyophilization: Physico-chemical fundamentals, freezing methods and consequences on process performance and quality attributes of biopharmaceuticals. Eur. J. Pharm. Biopharm. 2011, 78, 248–263. [Google Scholar] [CrossRef]
- Nakagawa, K.; Hottot, A.; Vessot, S.; Andrieu, J. Modeling of freezing step during freeze-drying of drugs in vials. AIChE J. 2007, 53, 1362–1372. [Google Scholar] [CrossRef]
- Pisano, R. Lyophilization of Pharmaceuticals and Biologicals; Methods in Pharmacology and Toxicology; Springer: New York, NY, USA, 2019; pp. 79–111. [Google Scholar] [CrossRef]
- Patel, S.M.; Bhugra, C.; Pikal, M.J. Reduced pressure ice fog technique for controlled ice nucleation during freeze-drying. AAPS PharmSciTech 2009, 10, 1406–1411. [Google Scholar] [CrossRef] [PubMed]
- Petersen, A.; Schneider, H.; Rau, G.; Glasmacher, B. A new approach for freezing of aqueous solutions under active control of the nucleation temperature. Cryobiology 2006, 53, 248–257. [Google Scholar] [CrossRef] [PubMed]
- Inada, T.; Zhang, X.; Yabe, A.; Kozawa, Y. Active control of phase change from supercooled water to ice by ultrasonic vibration 1. Control of freezing temperature. Int. J. Heat Mass Transf. 2001, 44, 4523–4531. [Google Scholar] [CrossRef]
- Nakagawa, K.; Hottot, A.; Vessot, S.; Andrieu, J. Influence of controlled nucleation by ultrasounds on ice morphology of frozen formulations for pharmaceutical proteins freeze-drying. Chem. Eng. Process. Process Intensif. 2006, 45, 783–791. [Google Scholar] [CrossRef]
- Hottot, A.; Nakagawa, K.; Andrieu, J. Effect of ultrasound-controlled nucleation on structural and morphological properties of freeze-dried mannitol solutions. Chem. Eng. Res. Des. 2008, 86, 193–200. [Google Scholar] [CrossRef]
- Passot, S.; Tréléa, I.C.; Marin, M.; Galan, M.; Morris, G.J.; Fonseca, F. Effect of controlled ice nucleation on primary drying stage and protein recovery in vials cooled in a modified freeze-dryer. J. Biomech. Eng. 2009, 131, 74511. [Google Scholar] [CrossRef] [PubMed]
- Kramer, M.; Sennhenn, B.; Lee, G. Freeze-drying using vacuum-induced surface freezing. J. Pharm. Sci. 2002, 91, 433–443. [Google Scholar] [CrossRef] [PubMed]
- Cochet, N.; Widehem, P. Ice crystallization by Pseudomonas syringae. Appl. Microbiol. Biotechnol. 2000, 54, 153–161. [Google Scholar] [CrossRef]
- Assegehegn, G.; Brito-de la Fuente, E.; Franco, J.M.; Gallegos, C. The Importance of Understanding the Freezing Step and Its Impact on Freeze-Drying Process Performance. J. Pharm. Sci. 2019, 108, 1378–1395. [Google Scholar] [CrossRef] [PubMed]
- Searles, J.A.; Carpenter, J.F.; Randolph, T.W. The ice nucleation temperature determines the primary drying rate of lyophilization for samples frozen on a temperature-controlled shelf. J. Pharm. Sci. 2001, 90, 860–871. [Google Scholar] [CrossRef]
- Nakagawa, K.; Hottot, A.; Vessot, S.; Andrieu, J. Modeling of freezing step during vial freeze-drying of pharmaceuticals—Influence of nucleation temperature on primary drying rate. Asia-Pac. J. Chem. Eng. 2011, 6, 288–293. [Google Scholar] [CrossRef]
- Mortier, S.T.F.C.; Gernaey, K.V.; De Beer, T.; Nopens, I. Global sensitivity analysis applied to drying models for one or a population of granules. AIChE J. 2014, 60, 1700–1717. [Google Scholar] [CrossRef]
- Mortier, S.T.F.C.; Van Bockstal, P.J.; Corver, J.; Nopens, I.; Gernaey, K.V.; De Beer, T. Uncertainty analysis as essential step in the establishment of the dynamic Design Space of primary drying during freeze-drying. Eur. J. Pharm. Biopharm. 2016, 103, 71–83. [Google Scholar] [CrossRef] [PubMed]
- Pisano, R.; Capozzi, L.C. Prediction of product morphology of lyophilized drugs in the case of Vacuum Induced Surface Freezing. Chem. Eng. Res. Des. 2017, 125, 119–129. [Google Scholar] [CrossRef]
- Van Bockstal, P.J.; Mortier, S.T.F.C.; Corver, J.; Nopens, I.; Gernaey, K.V.; De Beer, T. Global Sensitivity Analysis as Good Modelling Practices tool for the identification of the most influential process parameters of the primary drying step during freeze-drying. Eur. J. Pharm. Biopharm. 2018, 123, 108–116. [Google Scholar] [CrossRef] [Green Version]
- Van Bockstal, P.J.; Corver, J.; Mortier, S.T.F.C.; De Meyer, L.; Nopens, I.; Gernaey, K.V.; De Beer, T. Developing a framework to model the primary drying step of a continuous freeze-drying process based on infrared radiation. Eur. J. Pharm. Biopharm. 2018, 127, 159–170. [Google Scholar] [CrossRef] [PubMed]
- Van Bockstal, P.J.; Corver, J.; De Meyer, L.; Vervaet, C.; De Beer, T. Thermal Imaging as a Noncontact Inline Process Analytical Tool for Product Temperature Monitoring during Continuous Freeze-Drying of Unit Doses. Anal. Chem. 2018, 90, 13591–13599. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nicholas, J.V.; White, D.R. Use of Thermometers. Traceable Temperatures: An Introduction to Temperature Measurement and Calibration, 2nd ed.; Wiley: Hoboken, NJ, USA, 2001; pp. 125–158. [Google Scholar] [CrossRef]
- Majdak, M.; Jaremkiewicz, M. The analysis of thermocouple time constants as a function of fluid velocity. Meas. Autom. Monit. 2016, 62, 284–287. [Google Scholar]
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y. Handbook of Heat Transfer, 3rd ed.; McGraw Hill: New York, NY, USA, 1997; pp. 1–36. [Google Scholar]
- Jeng, T.M.; Tzeng, S.C.; Xu, R. Heat transfer characteristics of a rotating cylinder with a lateral air impinging jet. Int. J. Heat Mass Transf. 2014, 70, 235–249. [Google Scholar] [CrossRef]
- Sammut, C.; Webb, G.I. (Eds.) Cross-Validation. In Encyclopedia of Machine Learning; Springer: Boston, MA, USA, 2010; pp. 600–601. [Google Scholar] [CrossRef]
- Ortuño, M.; Márquez, A.; Gallego, S.; Neipp, C.; Beléndez, A. An experiment in heat conduction using hollow cylinders. Eur. J. Phys. 2011, 32, 1065–1075. [Google Scholar] [CrossRef]
- Searles, J.A. Freezing and annealing phenomena in lyophilization. In Freeze-Drying/Lyophilization of Pharmaceutical and Biological Products; CRC Press: Boca Raton, FL, USA, 2004; pp. 109–145. [Google Scholar]
- Saltelli, A. The Critique of Modelling and Sensitivity Analysis in the Scientific Discourse; European Commission, Joint Research Centre: Luxembourg, 2006; ISBN 92-79-03130-9. [Google Scholar]
- Van Bockstal, P.J.; Mortier, S.T.F.C.; Corver, J.; Nopens, I.; Gernaey, K.V.; De Beer, T. Quantitative risk assessment via uncertainty analysis in combination with error propagation for the determination of the dynamic Design Space of the primary drying step during freeze-drying. Eur. J. Pharm. Biopharm. 2017, 121, 32–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Colucci, D.; Fissore, D.; Barresi, A.A.; Braatz, R.D. A new mathematical model for monitoring the temporal evolution of the ice crystal size distribution during freezing in pharmaceutical solutions. Eur. J. Pharm. Biopharm. 2020, 148, 148–159. [Google Scholar] [CrossRef] [PubMed]
- Rowe, T. A technique for the nucleation of ice. In Proceedings of the International Symposium on Biological Product Freeze-Drying and Formulation, Bethesda, MD, USA, 24–26 October 1990. [Google Scholar]
- Konstantinidis, A.K.; Kuu, W.; Otten, L.; Nail, S.L.; Sever, R.R. Controlled nucleation in freeze-drying: Effects on pore size in the dried product layer, mass transfer resistance, and primary drying rate. J. Pharm. Sci. 2011, 100, 3453–3470. [Google Scholar] [CrossRef]
- AboulFotouh, K.; Cui, Z.; Williams, R.O., 3rd. Next-Generation COVID-19 Vaccines Should Take Efficiency of Distribution into Consideration. AAPS Pharm. Sci. Tech. 2021, 22, 126. [Google Scholar] [CrossRef]
- Miller, M.A.; Rodrigues, M.A.; Glass, M.A.; Singh, S.K.; Johnston, K.P.; Maynard, J.A. Frozen-state storage stability of a monoclonal antibody: Aggregation is impacted by freezing rate and solute distribution. J. Pharm. Sci. 2013, 102, 1194–1208. [Google Scholar] [CrossRef]
- Hansen, L.J.J.; Daoussi, R.; Vervaet, C.; Remon, J.P.; De Beer, T.R.M. Freeze-drying of live virus vaccines: A review. Vaccine 2015, 33, 5507–5519. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hauptmann, A.; Podgoršek, K.; Kuzman, D.; Srčič, S.; Hoelzl, G.; Loerting, T. Impact of Buffer, Protein Concentration and Sucrose Addition on the Aggregation and Particle Formation during Freezing and Thawing. Pharm. Res. 2018, 35, 101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roy, I.; Gupta, M.N. Freeze-drying of proteins: Some emerging concerns. Biotechnol. Appl. Biochem. 2004, 39, 165–177. [Google Scholar] [CrossRef] [PubMed]
- Aly, R.M. Current state of stem cell-based therapies: An overview. Stem Cell Investig. 2020, 7, 8. [Google Scholar] [CrossRef] [PubMed]
- Baboo, J.; Kilbride, P.; Delahaye, M.; Milne, S.; Fonseca, F.; Blanco, M.; Meneghel, J.; Nancekievill, A.; Gaddum, N.; Morris, G.J. The Impact of Varying Cooling and Thawing Rates on the Quality of Cryopreserved Human Peripheral Blood T Cells. Sci. Rep. 2019, 9, 3417. [Google Scholar] [CrossRef] [PubMed]
- Natan, D.; Nagler, A.; Arav, A. Freeze-drying of mononuclear cells derived from umbilical cord blood followed by colony formation. PLoS ONE 2009, 4, e5240. [Google Scholar] [CrossRef] [PubMed]
- Meneghel, J.; Kilbride, P.; Morris, G.J. Cryopreservation as a Key Element in the Successful Delivery of Cell-Based Therapies—A Review. Front. Med. 2020, 7, 592242. [Google Scholar] [CrossRef]
- Rockinger, U.; Funk, M.; Winter, G. Current Approaches of Preservation of Cells During (freeze-) Drying. J. Pharm. Sci. 2021, 110, 2873–2893. [Google Scholar] [CrossRef] [PubMed]








| Factor | Uncertainty Value | Reason of Inclusion |
|---|---|---|
| h (W/(mK)) | RMSE on regression model | |
| (m) | Uncertainty of vial properties | |
| (kg) | Uncertainty of vial properties | |
| (kg) | Measurement error | |
| (m/s) | Uncertainty of the gas flow rate measurement | |
| (C) | 2 | Uncertainty of the infrared temperature measurement |
| (C) | 2 | Uncertainty of the gas temperature measurement |
| Gas Flow Rate (L/min) | Cooling Rate Liquid Cooling Phase C/min) | Cooling Rate Solid Cooling Phase C/min) | Length Crystallization Phase (s) | Outer Vial Wall C) | Inner Vial Wall C) |
|---|---|---|---|---|---|
| 20 | 18.5 | 14.3 | 161 | −10.6 | −1.8 |
| 26 | 24.6 | 25.7 | 134 | −10.8 | −0.4 |
| 32 | 25.0 | 28.6 | 123 | −9.0 | −0.6 |
| 38 | 27.4 | 26.3 | 115 | −9.6 | −0.3 |
| 44 | 25.8 | 26.7 | 116 | −8.7 | −0.9 |
| 50 | 33.6 | 54.5 | 87 | −11.4 | −2.0 |
| 56 | 38.7 | 67.1 | 80 | −12.1 | −0.5 |
| 62 | 53.8 | 79.3 | 65 | −14.4 | −0.9 |
| 68 | 47.0 | 91.3 | 66 | −13.7 | −0.5 |
| 80 | 46.5 | 82.9 | 60 | −13.2 | −0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nuytten, G.; Revatta, S.R.; Van Bockstal, P.-J.; Kumar, A.; Lammens, J.; Leys, L.; Vanbillemont, B.; Corver, J.; Vervaet, C.; De Beer, T. Development and Application of a Mechanistic Cooling and Freezing Model of the Spin Freezing Step within the Framework of Continuous Freeze-Drying. Pharmaceutics 2021, 13, 2076. https://doi.org/10.3390/pharmaceutics13122076
Nuytten G, Revatta SR, Van Bockstal P-J, Kumar A, Lammens J, Leys L, Vanbillemont B, Corver J, Vervaet C, De Beer T. Development and Application of a Mechanistic Cooling and Freezing Model of the Spin Freezing Step within the Framework of Continuous Freeze-Drying. Pharmaceutics. 2021; 13(12):2076. https://doi.org/10.3390/pharmaceutics13122076
Chicago/Turabian StyleNuytten, Gust, Susan Ríos Revatta, Pieter-Jan Van Bockstal, Ashish Kumar, Joris Lammens, Laurens Leys, Brecht Vanbillemont, Jos Corver, Chris Vervaet, and Thomas De Beer. 2021. "Development and Application of a Mechanistic Cooling and Freezing Model of the Spin Freezing Step within the Framework of Continuous Freeze-Drying" Pharmaceutics 13, no. 12: 2076. https://doi.org/10.3390/pharmaceutics13122076
APA StyleNuytten, G., Revatta, S. R., Van Bockstal, P. -J., Kumar, A., Lammens, J., Leys, L., Vanbillemont, B., Corver, J., Vervaet, C., & De Beer, T. (2021). Development and Application of a Mechanistic Cooling and Freezing Model of the Spin Freezing Step within the Framework of Continuous Freeze-Drying. Pharmaceutics, 13(12), 2076. https://doi.org/10.3390/pharmaceutics13122076