Assessment and Modeling of Plasmonic Photothermal Therapy Delivered via a Fiberoptic Microneedle Device Ex Vivo
Abstract
:1. Introduction
2. Materials and Methods
2.1. Tissue Sample Collection
2.2. GNRs Synthesis and Photothermal Heating
2.3. Tissue Photothermal Heating with Collimated Laser Beam
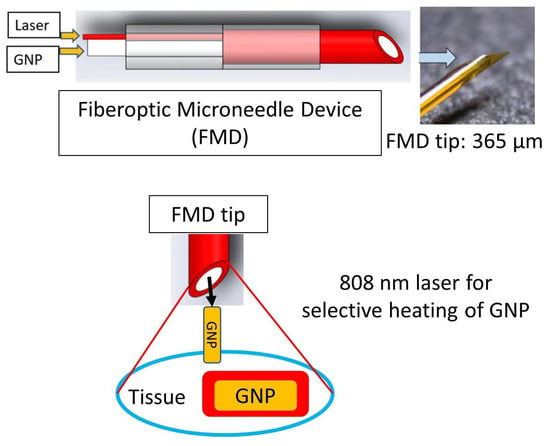
2.4. Tissue Photothermal Heating with FMD and with/without the GNRs
GNR Infusion and Tissue Photothermal Heating through FMD
2.5. Computational Modelling of Laser–Tissue Interaction
3. Results and Discussion
3.1. Results of GNRs’ Synthesis and Photothermal Heating
3.2. Results of Tissue Photothermal Heating by Collimated Laser Beam
3.3. Results of Tissue Photothermal Heating by FMD and with/without GNRs
3.4. Results of Computational Modelling
4. Conclusions
5. Patents
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rahib, L.; Smith, B.D.; Aizenberg, R.; Rosenzweig, A.B.; Fleshman, J.M.; Matrisian, L.M. Projecting cancer incidence and deaths to 2030: The unexpected burden of thyroid, liver, and pancreas cancers in the United States. Cancer Res. 2014, 74, 2913–2921. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2016. CA A Cancer J. Clin. 2016, 66, 7–30. [Google Scholar] [CrossRef] [Green Version]
- Strobel, O.; Neoptolemos, J.; Jäger, D.; Büchler, M.W. Optimizing the outcomes of pancreatic cancer surgery. Nat. Rev. Clin. Oncol. 2019, 16, 11–26. [Google Scholar] [CrossRef] [PubMed]
- Aslan, M.; Shahbazi, R.; Ulubayram, K.; Ozpolat, B. Targeted Therapies for Pancreatic Cancer and Hurdles Ahead. Anticancer Res. 2018, 38, 6591. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Jain, P.K.; El-Sayed, I.H.; El-Sayed, M.A. Plasmonic photothermal therapy (PPTT) using gold nanoparticles. Lasers Med. Sci. 2008, 23, 217. [Google Scholar] [CrossRef] [PubMed]
- Di Matteo, F.M.; Saccomandi, P.; Martino, M.; Pandolfi, M.; Pizzicannella, M.; Balassone, V.; Schena, E.; Pacella, C.M.; Silvestri, S.; Costamagna, G. Feasibility of EUS-guided Nd: YAG laser ablation of unresectable pancreatic adenocarcinoma. Gastrointest. Endosc. 2018, 88, 168–174. [Google Scholar] [CrossRef]
- Lee, E.S.; Lee, J.M. Imaging diagnosis of pancreatic cancer: A state-of-the-art review. World J. Gastroenterol. WJG 2014, 20, 7864. [Google Scholar] [CrossRef] [PubMed]
- Gaidhane, M.; Smith, I.; Ellen, K.; Gatesman, J.; Habib, N.; Foley, P.; Moskaluk, C.; Kahaleh, M. Endoscopic ultrasound-guided radiofrequency ablation (EUS-RFA) of the pancreas in a porcine model. Gastroenterol. Res. Pract. 2012, 2012, 431451. [Google Scholar] [CrossRef] [PubMed]
- Di Matteo, F.; Martino, M.; Rea, R.; Pandolfi, M.; Rabitti, C.; Masselli, G.M.P.; Silvestri, S.; Pacella, C.M.; Papini, E.; Panzera, F. EUS-guided Nd: YAG laser ablation of normal pancreatic tissue: A pilot study in a pig model. Gastrointest. Endosc. 2010, 72, 358–363. [Google Scholar] [CrossRef]
- Kennedy, L.C.; Bickford, L.R.; Lewinski, N.A.; Coughlin, A.J.; Hu, Y.; Day, E.S.; West, J.L.; Drezek, R.A. A new era for cancer treatment: Gold-nanoparticle-mediated thermal therapies. Small 2011, 7, 169–183. [Google Scholar] [CrossRef]
- Ali, M.R.K.; Wu, Y.; El-Sayed, M.A. Gold-nanoparticle-assisted plasmonic photothermal therapy advances toward clinical application. J. Phys. Chem. C 2019, 123, 15375–15393. [Google Scholar] [CrossRef]
- Huff, T.B.; Tong, L.; Zhao, Y.; Hansen, M.N.; Cheng, J.-X.; Wei, A. Hyperthermic effects of gold nanorods on tumor cells. Future Med. 2007, 2, 125. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.R.K.; Ibrahim, I.M.; Ali, H.R.; Selim, S.A.; El-Sayed, M.A. Treatment of natural mammary gland tumors in canines and felines using gold nanorods-assisted plasmonic photothermal therapy to induce tumor apoptosis. Int. J. Nanomed. 2016, 11, 4849. [Google Scholar]
- Wan, H.; Yue, J.; Zhu, S.; Uno, T.; Zhang, X.; Yang, Q.; Yu, K.; Hong, G.; Wang, J.; Li, L. A bright organic NIR-II nanofluorophore for three-dimensional imaging into biological tissues. Nat. Commun. 2018, 9, 1171. [Google Scholar] [CrossRef]
- Bayazitoglu, Y.; Kheradmand, S.; Tullius, T.K. An overview of nanoparticle assisted laser therapy. Int. J. Heat Mass Transf. 2013, 67, 469–486. [Google Scholar] [CrossRef]
- Jain, P.K.; Lee, K.S.; El-Sayed, I.H.; El-Sayed, M.A. Calculated absorption and scattering properties of gold nanoparticles of different size, shape, and composition: Applications in biological imaging and biomedicine. J. Phys. Chem. B 2006, 110, 7238–7248. [Google Scholar] [CrossRef] [Green Version]
- Costantini, P.E.; Di Giosia, M.; Ulfo, L.; Petrosino, A.; Saporetti, R.; Fimognari, C.; Pompa, P.P.; Danielli, A.; Turrini, E.; Boselli, L. Spiky Gold Nanoparticles for the Photothermal Eradication of Colon Cancer Cells. Nanomaterials 2021, 11, 1608. [Google Scholar] [CrossRef]
- Liu, S.; Pan, X.; Liu, H. Two-dimensional nanomaterials for photothermal therapy. Angew. Chem. 2020, 132, 5943–5953. [Google Scholar] [CrossRef]
- Saha, S.; Xiong, X.; Chakraborty, P.K.; Shameer, K.; Arvizo, R.R.; Kudgus, R.A.; Dwivedi, S.K.D.; Hossen, M.N.; Gillies, E.M.; Robertson, J.D. Gold nanoparticle reprograms pancreatic tumor microenvironment and inhibits tumor growth. ACS Nano 2016, 10, 10636–10651. [Google Scholar] [CrossRef]
- Zhou, F.; Yang, J.; Zhang, Y.; Liu, M.; Lang, M.L.; Li, M.; Chen, W.R. Local phototherapy synergizes with immunoadjuvant for treatment of pancreatic cancer through induced immunogenic tumor vaccine. Clin. Cancer Res. 2018, 24, 5335–5346. [Google Scholar] [CrossRef] [Green Version]
- Patino, T.; Mahajan, U.; Palankar, R.; Medvedev, N.; Walowski, J.; Münzenberg, M.; Mayerle, J.; Delcea, M. Multifunctional gold nanorods for selective plasmonic photothermal therapy in pancreatic cancer cells using ultra-short pulse near-infrared laser irradiation. Nanoscale 2015, 7, 5328–5337. [Google Scholar] [CrossRef]
- Vines, J.B.; Yoon, J.-H.; Ryu, N.-E.; Lim, D.-J.; Park, H. Gold nanoparticles for photothermal cancer therapy. Front. Chem. 2019, 7, 167. [Google Scholar] [CrossRef] [Green Version]
- Huai, Y.; Zhang, Y.; Xiong, X.; Das, S.; Bhattacharya, R.; Mukherjee, P. Gold Nanoparticles sensitize pancreatic cancer cells to gemcitabine. Cell Stress 2019, 3, 267. [Google Scholar] [CrossRef] [Green Version]
- Manrique-Bedoya, S.; Abdul-Moqueet, M.; Lopez, P.; Gray, T.; Disiena, M.; Locker, A.; Kwee, S.; Tang, L.; Hood, R.L.; Feng, Y. Multiphysics Modeling of Plasmonic Photothermal Heating Effects in Gold Nanoparticles and Nanoparticle Arrays. J. Phys. Chem. C 2020, 124, 17172–17182. [Google Scholar] [CrossRef]
- Nikoobakht, B.; El-Sayed, M.A. Preparation and growth mechanism of gold nanorods (NRs) using seed-mediated growth method. Chem. Mater. 2003, 15, 1957–1962. [Google Scholar] [CrossRef]
- Vigderman, L.; Zubarev, E.R. High-yield synthesis of gold nanorods with longitudinal SPR peak greater than 1200 nm using hydroquinone as a reducing agent. Chem. Mater. 2013, 25, 1450–1457. [Google Scholar] [CrossRef]
- Ali, M.R.K.; Snyder, B.; El-Sayed, M.A. Synthesis and optical properties of small Au nanorods using a seedless growth technique. Langmuir 2012, 28, 9807–9815. [Google Scholar] [CrossRef]
- Pulagam, K.R.; Henriksen-Lacey, M.; Uribe, K.B.; Renero-Lecuna, C.; Kumar, J.; Charalampopoulou, A.; Facoetti, A.; Protti, N.; Gómez-Vallejo, V.; Baz, Z. In Vivo Evaluation of Multifunctional Gold Nanorods for Boron Neutron Capture and Photothermal Therapies. ACS Appl. Mater. Interfaces 2021, 13, 49589–49601. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.R.K.; Rahman, M.A.; Wu, Y.; Han, T.; Peng, X.; Mackey, M.A.; Wang, D.; Shin, H.J.; Chen, Z.G.; Xiao, H. Efficacy, long-term toxicity, and mechanistic studies of gold nanorods photothermal therapy of cancer in xenograft mice. Proc. Natl. Acad. Sci. USA 2017, 114, E3110–E3118. [Google Scholar] [CrossRef] [Green Version]
- Polo, E.; Araban, V.; Pelaz, B.; Alvarez, A.; Taboada, P.; Mahmoudi, M.; del Pino, P. Photothermal effects on protein adsorption dynamics of PEGylated gold nanorods. Appl. Mater. Today 2019, 15, 599–604. [Google Scholar] [CrossRef]
- Akhter, F.; Bascos, G.N.W.; Canelas, M.; Griffin, B.; Hood, R.L. Mechanical characterization of a fiberoptic microneedle device for controlled delivery of fluids and photothermal excitation. J. Mech. Behav. Biomed. Mater. 2020, 112, 104042. [Google Scholar] [CrossRef] [PubMed]
- Hood, R.L.; Andriani, R.T.; Ecker, T.E.; Robertson, J.L.; Rylander, C.G. Characterizing Thermal Augmentation of Convection-Enhanced Drug Delivery with the Fiberoptic Microneedle Device. Engineering 2015, 1, 344–350. [Google Scholar] [CrossRef] [Green Version]
- Hood, R.L.; Rossmeisl, J.H., Jr.; Andriani, R.T., Jr.; Wilkinson, A.R.; Robertson, J.L.; Rylander, C.G. Intracranial hyperthermia through local photothermal heating with a fiberoptic microneedle device. Lasers Surg. Med. 2013, 45, 167–174. [Google Scholar] [CrossRef]
- Hood, R.L.; Carswell, W.F.; Rodgers, A.; Kosoglu, M.A.; Rylander, M.N.; Grant, D.; Robertson, J.L.; Rylander, C.G. Spatially controlled photothermal heating of bladder tissue through single-walled carbon nanohorns delivered with a fiberoptic microneedle device. Lasers Med. Sci. 2013, 28, 1143–1150. [Google Scholar] [CrossRef]
- Hood, R.L.; Andriani, R.T., Jr.; Emch, S.; Robertson, J.L.; Rylander, C.G.; Rossmeisl, J.H., Jr. Fiberoptic microneedle device facilitates volumetric infusate dispersion during convection-enhanced delivery in the brain. Lasers Surg. Med. 2013, 45, 418–426. [Google Scholar] [CrossRef]
- Niemz, M.H. Laser-Tissue Interactions; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Rylander, M.N.; Feng, Y.; Bass, J.O.N.; Diller, K.R. Thermally induced injury and heat-shock protein expression in cells and tissues. Ann. N. Y. Acad. Sci. 2005, 1066, 222. [Google Scholar] [CrossRef]
- Feng, Y.; Fuentes, D.; Hawkins, A.; Bass, J.; Rylander, M.N.; Elliott, A.; Shetty, A.; Stafford, R.J.; Oden, J.T. Nanoshell-mediated laser surgery simulation for prostate cancer treatment. Eng. Comput. 2009, 25, 3–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saccomandi, P.; Schena, E.; Caponero, M.A.; Di Matteo, F.M.; Martino, M.; Pandolfi, M.; Silvestri, S. Theoretical analysis and experimental evaluation of laser-induced interstitial thermotherapy in ex vivo porcine pancreas. IEEE Trans. Biomed. Eng. 2012, 59, 2958–2964. [Google Scholar] [CrossRef]
- Akhter, F.; Manrique-Bedoya, S.; Moreau, C.; Smith, A.L.; Feng, Y.; Mayer, K.M.; Hood, R.L. Characterization of Thermal and Optical Properties in Porcine Pancreas Tissue (Submitted and in Review). Lasers Surg. Med. 2021, in press. [Google Scholar]
- Wex, C.; Fröhlich, M.; Brandstädter, K.; Bruns, C.; Stoll, A. Experimental analysis of the mechanical behavior of the viscoelastic porcine pancreas and preliminary case study on the human pancreas. J. Mech. Behav. Biomed. Mater. 2015, 41, 199–207. [Google Scholar] [CrossRef] [PubMed]
- Nicoli, S.; Ferrari, G.; Quarta, M.; Macaluso, C.; Govoni, P.; Dallatana, D.; Santi, P. Porcine sclera as a model of human sclera for in vitro transport experiments: Histology, SEM, and comparative permeability. Mol. Vis. 2009, 15, 259. [Google Scholar]
- Abràmoff, M.D.; Magalhães, P.J.; Ram, S.J. Image processing with ImageJ. Biophotonics Int. 2004, 11, 36–42. [Google Scholar]
- Jana, N.R.; Gearheart, L.; Murphy, C.J. Wet chemical synthesis of high aspect ratio cylindrical gold nanorods. J. Phys. Chem. B 2001, 105, 4065–4067. [Google Scholar] [CrossRef]
- Jana, N.R.; Gearheart, L.; Murphy, C.J. Seed-mediated growth approach for shape-controlled synthesis of spheroidal and rod-like gold nanoparticles using a surfactant template. Adv. Mater. 2001, 13, 1389–1393. [Google Scholar] [CrossRef]
- Feng, Y.; Fuentes, D.; Stafford, R.J.; Oden, J.T. Model-based real-time control for laser induced thermal therapy with applications to prostate cancer treatment. In Optical Interactions with Tissue and Cells XX; International Society for Optics and Photonics: Washington, DC, USA, 2009; p. 717515. [Google Scholar]
- Charny, C.K. Mathematical models of bioheat transfer. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1992; Volume 22, pp. 19–155. [Google Scholar]
- Chandrasekhar, S. Radiative Transfer; Courier Corporation: Boston, MA, USA, 2013. [Google Scholar]
- Graaff, R.; Ten Bosch, J.J. Diffusion coefficient in photon diffusion theory. Opt. Lett. 2000, 25, 43–45. [Google Scholar] [CrossRef] [PubMed]
- Nakai, T.; Nishimura, G.; Yamamoto, K.; Tamura, M. Expression of optical diffusion coefficient in high-absorption turbid media. Phys. Med. Biol. 1997, 42, 2541. [Google Scholar] [CrossRef] [PubMed]
- Cheng, A.H.D.; Cheng, D.T. Heritage and early history of the boundary element method. Eng. Anal. Bound. Elem. 2005, 29, 268–302. [Google Scholar] [CrossRef]
- Mohammadi, A.; Bianchi, L.; Asadi, S.; Saccomandi, P. Measurement of Ex Vivo Liver, Brain and Pancreas Thermal Properties as Function of Temperature. Sensors 2021, 21, 4236. [Google Scholar] [CrossRef]
- Agafonkina, I.V.; Belozerov, A.G.; Vasilyev, A.O.; Pushkarev, A.V.; Tsiganov, D.I.; Shakurov, A.V.; Zherdev, A.A. Thermal Properties of Human Soft Tissue and Its Equivalents in a Wide Low-Temperature Range. J. Eng. Phys. Thermophys. 2021, 94, 233–246. [Google Scholar] [CrossRef]
- Simon, H.B. Hyperthermia. N. Engl. J. Med. 1993, 329, 483–487. [Google Scholar]
- Niidome, T.; Yamagata, M.; Okamoto, Y.; Akiyama, Y.; Takahashi, H.; Kawano, T.; Katayama, Y.; Niidome, Y. PEG-modified gold nanorods with a stealth character for in vivo applications. J. Control. Release 2006, 114, 343–347. [Google Scholar] [CrossRef] [PubMed]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2004, 58, 5007. [Google Scholar] [CrossRef]
- Li, B.; Lu, L.; Zhao, M.; Lei, Z.; Zhang, F. An efficient 1064 nm NIR-II excitation fluorescent molecular dye for deep-tissue high-resolution dynamic bioimaging. Angew. Chem. 2018, 130, 7605–7609. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akhter, F.; Manrique-Bedoya, S.; Moreau, C.; Smith, A.L.; Feng, Y.; Mayer, K.M.; Hood, R.L. Assessment and Modeling of Plasmonic Photothermal Therapy Delivered via a Fiberoptic Microneedle Device Ex Vivo. Pharmaceutics 2021, 13, 2133. https://doi.org/10.3390/pharmaceutics13122133
Akhter F, Manrique-Bedoya S, Moreau C, Smith AL, Feng Y, Mayer KM, Hood RL. Assessment and Modeling of Plasmonic Photothermal Therapy Delivered via a Fiberoptic Microneedle Device Ex Vivo. Pharmaceutics. 2021; 13(12):2133. https://doi.org/10.3390/pharmaceutics13122133
Chicago/Turabian StyleAkhter, Forhad, Santiago Manrique-Bedoya, Chris Moreau, Andrea Lynn Smith, Yusheng Feng, Kathryn M. Mayer, and R. Lyle Hood. 2021. "Assessment and Modeling of Plasmonic Photothermal Therapy Delivered via a Fiberoptic Microneedle Device Ex Vivo" Pharmaceutics 13, no. 12: 2133. https://doi.org/10.3390/pharmaceutics13122133
APA StyleAkhter, F., Manrique-Bedoya, S., Moreau, C., Smith, A. L., Feng, Y., Mayer, K. M., & Hood, R. L. (2021). Assessment and Modeling of Plasmonic Photothermal Therapy Delivered via a Fiberoptic Microneedle Device Ex Vivo. Pharmaceutics, 13(12), 2133. https://doi.org/10.3390/pharmaceutics13122133