Understanding the pH Dependence of Supersaturation State—A Case Study of Telmisartan
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. pKa Measurement by UV and NMR
2.2.1. UV/pH Titrations in Aqueous Solutions
2.2.2. UV/pH Titrations in Methanol-Water Mixtures
H NMR/pH Titrations
2.3. Kinetic Solubility Measurement
2.4. Thermodynamic Solubility Measurement
2.5. XRD
2.6. Analysis of Solubility-pH Data
2.7. Mass Spectrometry
2.8. Computational Methods for Studying Dimerization
3. Results and Discussion
3.1. pKa Determination by UV, Potentiometric and NMR Methods
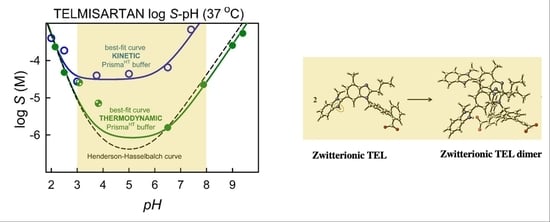
3.2. Kinetic Solubility Measurements
3.3. Thermodynamic Solubility and XRD Results
3.4. Mass Spectrometry
3.5. Studying Dimerization by Computational Chemistry
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Szabó, E.; Záhonyi, P.; Brecska, D.; Galata, D.L.; Mészáros, L.A.; Madarász, L.; Csorba, K.; Vass, P.; Hirsch, E.; Szafraniec-Szczȩsny, J.; et al. Comparison of Amorphous Solid Dispersions of Spironolactone Prepared by Spray Drying and Electrospinning: The Influence of the Preparation Method on the Dissolution Properties. Mol. Pharm. 2021, 18, 317–327. [Google Scholar] [CrossRef]
- Sóti, P.L.; Bocz, K.; Pataki, H.; Eke, Z.; Farkas, A.; Verreck, G.; Kiss, É.; Fekete, P.; Vigh, T.; Wagner, I.; et al. Comparison of spray drying, electroblowing and electrospinning for preparation of Eudragit E and itraconazole solid dispersions. Int. J. Pharm. 2015, 494, 23–30. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farkas, B.; Balogh, A.; Cselkó, R.; Molnár, K.; Farkas, A.; Borbás, E.; Marosi, G.; Nagy, Z.K. Corona alternating current electrospinning: A combined approach for increasing the productivity of electrospinning. Int. J. Pharm. 2019, 561, 219–227. [Google Scholar] [CrossRef]
- Taylor, L.S.; Zhang, G.G.Z. Physical chemistry of supersaturated solutions and implications for oral absorption. Adv. Drug Deliv. Rev. 2016, 101, 122–142. [Google Scholar] [CrossRef] [PubMed]
- Bauer-Brandl, A.; Brandl, M. Solubility and Supersaturation; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Fong, S.Y.K.; Bauer-Brandl, A.; Brandl, M. Oral bioavailability enhancement through supersaturation: An update and meta-analysis. Expert Opin. Drug Deliv. 2017, 14, 403–426. [Google Scholar] [CrossRef] [PubMed]
- Oki, J.; Watanabe, D.; Uekusa, T.; Sugano, K. Mechanism of Supersaturation Suppression in Dissolution Process of Acidic Drug Salt. Mol. Pharm. 2019, 16, 1669–1677. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Arora, K.; Mohapatra, H.; Sindhu, R.K.; Bulzan, M.; Cavalu, S.; Paneshar, G.; Elansary, H.O.; El-Sabrout, A.M.; Mahmoud, E.A.; et al. Supersaturation-Based Drug Delivery Systems: Strategy for Bioavailability Enhancement of Poorly Water-Soluble Drugs. Molecules 2022, 27, 2969. [Google Scholar] [CrossRef] [PubMed]
- Box, K.J.; Völgyi, G.; Baka, E.; Stuart, M.; Takács-Novák, K.; Comer, J.E.A. Equilibrium versus kinetic measurements of aqueous solubility, and the ability of compounds to supersaturate in solution—A validation study. J. Pharm. Sci. 2006, 95, 1298–1307. [Google Scholar] [CrossRef]
- Borbás, E.; Kádár, S.; Tsinman, K.; Tsinman, O.; Csicsák, D.; Takács-Novák, K.; Völgyi, G.; Sinkó, B.; Pataki, H. Prediction of Bioequivalence and Food Effect Using Flux- and Solubility-Based Methods. Mol. Pharm. 2019, 16, 4121–4130. [Google Scholar] [CrossRef] [Green Version]
- Ilevbare, G.A.; Taylor, L.S. Liquid-liquid phase separation in highly supersaturated aqueous solutions of poorly water-soluble drugs: Implications for solubility enhancing formulations. Cryst. Growth Des. 2013, 13, 1497–1509. [Google Scholar] [CrossRef]
- Raina, S.A.; Zhang, G.G.Z.; Alonzo, D.E.; Wu, J.; Zhu, D.; Catron, N.D.; Gao, Y.; Taylor, L.S. Impact of Solubilizing Additives on Supersaturation and Membrane Transport of Drugs. Pharm. Res. 2015, 32, 3350–3364. [Google Scholar] [CrossRef]
- Kádár, S.; Tőzsér, P.; Nagy, B.; Farkas, A.; Nagy, Z.K.; Tsinman, O.; Tsinman, K.; Csicsák, D.; Völgyi, G.; Takács-Novák, K.; et al. Flux-Based Formulation Development—A Proof of Concept Study. AAPS J. 2022, 24, 22. [Google Scholar] [CrossRef] [PubMed]
- Völgyi, G.; Ruiz, R.; Box, K.; Comer, J.; Bosch, E.; Takács-Novák, K. Potentiometric and spectrophotometric pKa determination of water-insoluble compounds: Validation study in a new cosolvent system. Anal. Chim. Acta 2007, 583, 418–428. [Google Scholar] [CrossRef] [PubMed]
- Tóth, G.; Jánoska, Á.; Völgyi, G.; Szabó, Z.I.; Orgován, G.; Mirzahosseini, A.; Noszál, B. Physicochemical Characterization and Cyclodextrin Complexation of the Anticancer Drug Lapatinib. J. Chem. 2017, 2017, 4537632. [Google Scholar] [CrossRef]
- Mirzahosseini, A.; Pálla, T.; Orgován, G.; Tóth, G.; Noszál, B. Dopamine: Acid-base properties and membrane penetration capacity. J. Pharm. Biomed. Anal. 2018, 158, 346–350. [Google Scholar] [CrossRef]
- Baka, E.; Comer, J.E.A.; Takács-Novák, K. Study of equilibrium solubility measurement by saturation shake-flask method using hydrochlorothiazide as model compound. J. Pharm. Biomed. Anal. 2008, 46, 335–341. [Google Scholar] [CrossRef]
- Avdeef, A.; Fuguet, E.; Llinàs, A.; Ràfols, C.; Bosch, E.; Völgyi, G.; Verbic, T.; Boldyreva, E.; Takács-Novák, K. Equilibrium solubility measurement of ionizable drugs-consensus recommendations for improving data quality. ADMET DMPK 2016, 4, 117–178. [Google Scholar] [CrossRef] [Green Version]
- Csicsák, D.; Borbás, E.; Kádár, S.; Tőzsér, P.; Bagi, P.; Pataki, H.; Sinkó, B.; Takács-Novák, K.; Völgyi, G. Towards more accurate solubility measurements with real time monitoring: A carvedilol case study. New J. Chem. 2021, 45, 11618–11625. [Google Scholar] [CrossRef]
- Takács-Novák, K.; Tempfli, D.; Csicsák, D.; Völgyi, G.; Borbás, E.; Nagy, Z.K.; Sinkó, B. Solubility analysis of venlafaxine hydrochloride polymorphs by shake-flask method and real time monitoring. Acta Pharm. Hung. 2019, 89, 88–96. [Google Scholar] [CrossRef]
- Tempfli, D.; Borbás, E.; Pataki, H.; Csicsák, D.; Völgyi, G.; Sinkó, B.; Takács-Novák, K. Revisit of solubility of oxytetracycline polymorphs. An old story in the light of new results. Eur. J. Pharm. Sci. 2020, 149, 105328. [Google Scholar] [CrossRef]
- Völgyi, G.; Csicsák, D.; Takács-Novák, K. Right filter-selection for phase separation in equilibrium solubility measurement. Eur. J. Pharm. Sci. 2018, 123, 98–105. [Google Scholar] [CrossRef]
- Avdeef, A. Anomalous solubility behavior of several acidic drugs. ADMET DMPK 2014, 2, 33–42. [Google Scholar] [CrossRef] [Green Version]
- Marković, O.S.; Pešić, M.P.; Shah, A.V.; Serajuddin, A.T.M.; Verbić, T.; Avdeef, A. Solubility-pH profile of desipramine hydrochloride in saline phosphate buffer: Enhanced solubility due to drug-buffer aggregates. Eur. J. Pharm. Sci. 2019, 133, 264–274. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuguet, E.; Subirats, X.; Ràfols, C.; Bosch, E.; Avdeef, A. Ionizable Drug Self-Associations and the Solubility Dependence on pH: Detection of Aggregates in Saturated Solutions Using Mass Spectrometry (ESI-Q-TOF-MS/MS). Mol. Pharm. 2021, 18, 2311–2321. [Google Scholar] [CrossRef]
- Marković, O.S.; Patel, N.G.; Serajuddin, A.T.M.; Avdeef, A.; Verbić, T.Z. Nortriptyline Hydrochloride Solubility-pH Profiles in a Saline Phosphate Buffer: Drug-Phosphate Complexes and Multiple pHmaxDomains with a Gibbs Phase Rule “soft” Constraints. Mol. Pharm. 2022, 19, 710–719. [Google Scholar] [CrossRef] [PubMed]
- Avdeef, A.; Sugano, K. Salt Solubility and Disproportionation–Uses and Limitations of Equations for pHmax and the In-silico Prediction of pHmax. J. Pharm. Sci. 2022, 111, 225–246. [Google Scholar] [CrossRef] [PubMed]
- Almeida, E.S.L.; Reutzel-Edens, S.M.; Stephenson, G.A.; Taylor, L.S. Assessment of the amorphous “solubility” of a group of diverse drugs using new experimental and theoretical approaches. Mol. Pharm. 2015, 12, 484–495. [Google Scholar] [CrossRef]
- Shah, N.; Sandhu, H.; Choi, D.S.; Kalb, O.; Page, S.; Wyttenbach, N. Structured Development Approach for Amorphous Systems. In Formulating Poorly Water Soluble Drugs; Springer: New York, NY, USA, 2012; pp. 267–310. [Google Scholar]
- Kirk, J.K. Angiotensin-II receptor antagonists: Their place in therapy. Am. Fam. Physician 1999, 59, 3140–3148. [Google Scholar]
- Tran, P.H.L.; Tran, H.T.T.; Lee, B.J. Modulation of microenvironmental pH and crystallinity of ionizable telmisartan using alkalizers in solid dispersions for controlled release. J. Control. Release 2008, 129, 59–65. [Google Scholar] [CrossRef]
- Kundu, S.; Kumari, N.; Soni, S.R.; Ranjan, S.; Kumar, R.; Sharon, A.; Ghosh, A. Enhanced Solubility of Telmisartan Phthalic Acid Cocrystals within the pH Range of a Systemic Absorption Site. ACS Omega 2018, 3, 15380–15388. [Google Scholar] [CrossRef] [Green Version]
- Cagigal, E.; González, L.; Alonso, R.M.; Jiménez, R.M. pKa determination of angiotensin II receptor antagonists (ARA II) by spectrofluorimetry. J. Pharm. Biomed. Anal. 2001, 26, 477–486. [Google Scholar] [CrossRef]
- Wienen, W.; Entzeroth, M.; Van Meel, J.C.A.; Stangier, J.; Busch, U.; Ebner, T.; Schmid, J.; Lehmann, H.; Matzek, K.; Kempthorne-Rawson, J.; et al. A review on telmisartan: A novel, long-acting angiotensin II-receptor antagonist. Cardiovasc. Drug Rev. 2000, 18, 127–154. [Google Scholar] [CrossRef]
- Muankaew, C.; Jansook, P.; Sigurcrossed, D.; Signsson, H.H.; Loftsson, T. Cyclodextrin-based telmisartan ophthalmic suspension: Formulation development for water-insoluble drugs. Int. J. Pharm. 2016, 507, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Marasini, N.; Tran, T.H.; Poudel, B.K.; Cho, H.J.; Choi, Y.K.; Chi, S.C.; Choi, H.G.; Yong, C.S.; Kim, J.O. Fabrication and evaluation of pH-modulated solid dispersion for telmisartan by spray-drying technique. Int. J. Pharm. 2013, 441, 424–432. [Google Scholar] [CrossRef]
- Tam, K.Y.; Takács-Novák, K. Multi-wavelength spectrophotometric determination of acid dissociation constants: A validation study. Anal. Chim. Acta 2001, 434, 157–167. [Google Scholar] [CrossRef]
- Völgyi, G.; Marosi, A.; Takács-Novák, K.; Avdeef, A. Salt solubility products of diprenorphine hydrochloride, codeine and lidocaine hydrochlorides and phosphates-novel method of data analysis not dependent on explicit solubility equations. ADMET DMPK 2013, 1, 48–62. [Google Scholar] [CrossRef]
- Orgován, G.; Noszál, B. Electrodeless, accurate pH determination in highly basic media using a new set of 1H NMR pH indicators. J. Pharm. Biomed. Anal. 2011, 54, 958–964. [Google Scholar] [CrossRef]
- Szakács, Z.; Hägele, G.; Tyka, R. 1H/31P NMR pH indicator series to eliminate the glass electrode in NMR spectroscopic pK a determinations. Anal. Chim. Acta 2004, 522, 247–258. [Google Scholar] [CrossRef]
- Szakács, Z.; Noszál, B. Protonation microequilibrium treatment of polybasic compounds with any possible symmetry. J. Math. Chem. 1999, 26, 139–155. [Google Scholar] [CrossRef]
- Avdeef, A. Phosphate precipitates and water-soluble aggregates in re-analyzed solubility-pH data of twenty-five basic drugs. ADMET DMPK 2014, 2, 43–55. [Google Scholar] [CrossRef]
- Avdeef, A. Suggested improvements for measurement of equilibrium solubility-pH of ionizable drugs. ADMET DMPK 2015, 3, 84–109. [Google Scholar] [CrossRef]
- Butcher, G.; Comer, J.; Avdeef, A. pKa-critical interpretations of solubility-pH Profiles: PG-300995 and NSC-639829 case studies. ADMET DMPK 2015, 3, 131–140. [Google Scholar] [CrossRef] [Green Version]
- Pobudkowska, A.; Ràfols, C.; Subirats, X.; Bosch, E.; Avdeef, A. Phenothiazines solution complexity–Determination of pKa and solubility-pH profiles exhibiting sub-micellar aggregation at 25 and 37 °C. Eur. J. Pharm. Sci. 2016, 93, 163–176. [Google Scholar] [CrossRef] [Green Version]
- Takács-Novák, K.; Urac, M.; Horváth, P.; Völgyi, G.; Anderson, B.D.; Avdeef, A. Equilibrium solubility measurement of compounds with low dissolution rate by Higuchi’s Facilitated Dissolution Method. A validation study. Eur. J. Pharm. Sci. 2017, 106, 133–141. [Google Scholar] [CrossRef] [PubMed]
- Lipparini, F.; Egidi, F.; Goings, J.; Peng, B.; Petrone, A.; Henderson, T.; Ranasinghe, D.; Zakrzewski, V.G.; Gao, J.; Rega, N.; et al. Gaussian 09, Revision E.01 2013; Gaussian Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Y.; Truhlar, D.G. Applications and validations of the Minnesota density functionals. Chem. Phys. Lett. 2011, 502, 1–13. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Tosco, P.; Rolando, B.; Fruttero, R.; Henchoz, Y.; Martel, S.; Carrupt, P.A.; Gasco, A. Physicochemical profiling of sartans: A detailed study of ionization constants and distribution coefficients. Helv. Chim. Acta 2008, 91, 468–482. [Google Scholar] [CrossRef]
- Wagner, L.; Zsigmond, Z.; Ujfalussy, G.; Orban, A.; Fulop, A. WO 2014/091263 Al 2014. Telmisartan Containing Pharmaceutical Composition. WO 2014/091263 Al 2014. Available online: https://patentscope2.wipo.int/search/en/detail.jsf?docId=WO2014091263 (accessed on 4 July 2022).
- Borbás, E.; Nagy, Z.K.; Nagy, B.; Balogh, A.; Farkas, B.; Tsinman, O.; Tsinman, K.; Sinkó, B. The effect of formulation additives on in vitro dissolution-absorption profile and in vivo bioavailability of telmisartan from brand and generic formulations. Eur. J. Pharm. Sci. 2018, 114, 310–317. [Google Scholar] [CrossRef]







| Method | Ionization Macroconstansts | ||
|---|---|---|---|
| pKa1 ± SD (Carboxyl Group) | pKa2 ± SD (Middle Benzimidazole Ring) | pKa3 ± SD (Terminal Benzimidazole Ring) | |
| UV/pH titration in aqueous medium (37 °C) | 3.04 ± 0.03 | 4.08 ± 0.02 | 5.91 ± 0.05 |
| UV/pH titration in aqueous medium (25 °C) | 3.03 ± 0.04 | 4.22 ± 0.09 | 6.08 ± 0.07 |
| UV/pH titration in MeOH-water mixture (25 °C) | 3.03 ± 0.06 | 4.19 ± 0.07 | 6.14 ± 0.10 |
| NMR-pH titration (25 °C) | 3.21 ± 0.14 | 4.28 ± 0.07 | 6.08 ± 0.04 |
| pH | S ± SD (µg/mL) | logS ± SD (M) | XRD Characterization |
|---|---|---|---|
| 1.60 | 150.00 ± 38.00 | −3.54 ± 0.05 | Crystalline |
| 2.15 | 119.01 ± 11.79 | −3.64 ± 0.04 | |
| 2.50 | 16.99 ± 0.72 | −4.32 ± 0.02 | |
| 3.08 | 13.05 ± 1.73 | −4.60 ± 0.06 | |
| 3.82 | 3.62 ± 0.59 | −5.15 ± 0.13 | |
| 6.50 | 0.79 ± 0.16 | −5.80 ± 0.15 | |
| 7.88 | 11.54 ± 0.26 | −4.65 ± 0.01 | |
| 9.00 | 130.41 ± 2.73 | −3.60 ± 0.01 | amorphous background |
| 9.40 | 274.95 ± 9.40 | −3.27 ± 0.02 | |
| 9.79 | 1472.67 ± 254.55 | −2.54 ± 0.07 | |
| 11.74 | 2250.10 ± 144.82 | −2.36 ± 0.03 | Amorphous |
| pH | S ± SD (µg/mL) | logS ± SD (M) |
|---|---|---|
| 2.16 | 147.72 ± 5.48 | −3.54 ± 0.02 |
| 2.66 | 10.83 ± 0.53 | −4.68 ± 0.02 |
| 3.08 | 3.4 ± 0.49 | −5.18 ± 0.06 |
| 3.98 | 0.36 ± 0.12 | −6.16 ± 0.15 |
| 7.22 | 3.65 ± 0.11 | −5.15 ± 0.01 |
| 7.4 | 13.80 ± 2.81 | −4.57 ± 0.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kádár, S.; Csicsák, D.; Tőzsér, P.; Farkas, A.; Pálla, T.; Mirzahosseini, A.; Tóth, B.; Tóth, G.; Fiser, B.; Horváth, P.; et al. Understanding the pH Dependence of Supersaturation State—A Case Study of Telmisartan. Pharmaceutics 2022, 14, 1635. https://doi.org/10.3390/pharmaceutics14081635
Kádár S, Csicsák D, Tőzsér P, Farkas A, Pálla T, Mirzahosseini A, Tóth B, Tóth G, Fiser B, Horváth P, et al. Understanding the pH Dependence of Supersaturation State—A Case Study of Telmisartan. Pharmaceutics. 2022; 14(8):1635. https://doi.org/10.3390/pharmaceutics14081635
Chicago/Turabian StyleKádár, Szabina, Dóra Csicsák, Petra Tőzsér, Attila Farkas, Tamás Pálla, Arash Mirzahosseini, Blanka Tóth, Gergő Tóth, Béla Fiser, Péter Horváth, and et al. 2022. "Understanding the pH Dependence of Supersaturation State—A Case Study of Telmisartan" Pharmaceutics 14, no. 8: 1635. https://doi.org/10.3390/pharmaceutics14081635
APA StyleKádár, S., Csicsák, D., Tőzsér, P., Farkas, A., Pálla, T., Mirzahosseini, A., Tóth, B., Tóth, G., Fiser, B., Horváth, P., Madarász, J., Avdeef, A., Takács-Novák, K., Sinkó, B., Borbás, E., & Völgyi, G. (2022). Understanding the pH Dependence of Supersaturation State—A Case Study of Telmisartan. Pharmaceutics, 14(8), 1635. https://doi.org/10.3390/pharmaceutics14081635