Computational Modeling on Drugs Effects for Left Ventricle in Cardiomyopathy Disease
Abstract
:1. Introduction
2. Materials and Methods
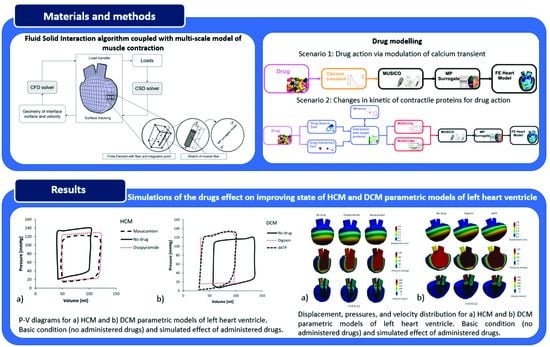
2.1. Fluid–Solid Coupling
2.2. Finite Element (FE) Solvers
2.3. Cardiomyopathy Risk Stratification
2.4. Drug Modeling
2.4.1. Drugs That Modulate [Ca2+] Transients
- Disopyramide
- b.
- Digoxin
2.4.2. Drugs That Affect Changes in Kinetic Parameters
- Mavacamten
- b.
- 2-Deoxy Adenosine Triphosphate (dATP)
3. Results
3.1. Cardiomyopathy Risk Stratification Tool
3.2. Simulations of the Effect of Drugs on Improving State of HCM and DCM Heart Models (PAK FE Solver Coupled with MP Surrogate Model)
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Elliott, P.; Anastasakis, A.; Borger, M.A.; Borggrefe, M.; Cecchi, F.; Charron, P.; Hagege, A.A.; Lafont, A.; Limongelli, G.; Mahrholdt, H.; et al. 2014 ESC Guidelines on Diagnosis and Management of Hypertrophic Cardiomyopathy. Eur. Heart J. 2014, 35, 2733–2779. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elliott, P.; Andersson, B.; Arbustini, E.; Bilinska, Z.; Cecchi, F.; Charron, P.; Dubourg, O.; Kuhl, U.; Maisch, B.; McKenna, W.J.; et al. Classification of the Cardiomyopathies: A Position Statement from the European Society of Cardiology Working Group on Myocardial and Pericardial Diseases. Eur. Heart J. 2007, 29, 270–276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McNally, E.M.; Golbus, J.R.; Puckelwartz, M.J. Genetic Mutations and Mechanisms in Dilated Cardiomyopathy. J. Clin. Investig. 2013, 123, 19–26. [Google Scholar] [CrossRef] [Green Version]
- Maron, M.S.; Olivotto, I.; Zenovich, A.G.; Link, M.S.; Pandian, N.G.; Kuvin, J.T.; Nistri, S.; Cecchi, F.; Udelson, J.E.; Maron, B.J. Hypertrophic Cardiomyopathy Is Predominantly a Disease of Left Ventricular Outflow Tract Obstruction. Circulation 2006, 114, 2232–2239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mijailovich, S.M.; Prodanovic, M.; Poggesi, C.; Powers, J.D.; Davis, J.; Geeves, M.A.; Regnier, M. The Effect of Variable Troponin C Mutation Thin Filament Incorporation on Cardiac Muscle Twitch Contractions. J. Mol. Cell. Cardiol. 2021, 155, 112–124. [Google Scholar] [CrossRef]
- Prodanovic, M.; Stojanovic, B.; Prodanovic, D.; Filipovic, N.; Mijailovich, S.M. Computational Modeling of Sarcomere Protein Mutations and Drug Effects on Cardiac Muscle Behavior. In Proceedings of the 2021 IEEE 21st International Conference on Bioinformatics and Bioengineering (BIBE), Kragujevac, Serbia, 25–27 October 2021; pp. 1–6. [Google Scholar]
- Stojanovic, B.; Svicevic, M.; Kaplarevic-Malisic, A.; Gilbert, R.J.; Mijailovich, S.M. Multi-Scale Striated Muscle Contraction Model Linking Sarcomere Length-Dependent Cross-Bridge Kinetics to Macroscopic Deformation. J. Comput. Sci. 2020, 39, 101062. [Google Scholar] [CrossRef]
- Mijailovich, S.M.; Fredberg, J.J.; Butler, J.P. On the Theory of Muscle Contraction: Filament Extensibility and the Development of Isometric Force and Stiffness. Biophys. J. 1996, 71, 1475–1484. [Google Scholar] [CrossRef] [Green Version]
- Ivanović, M.; Stojanović, B.; Kaplarević-Mališić, A.; Gilbert, R.; Mijailovich, S. Distributed Multi-Scale Muscle Simulation in a Hybrid MPI–CUDA Computational Environment. Simulation 2016, 92, 19–31. [Google Scholar] [CrossRef]
- Hill, T.L. Theoretical Formalism for the Sliding Filament Model of Contraction of Striated Muscle Part II. Prog. Biophys. Mol. Biol. 1976, 29, 105–159. [Google Scholar] [CrossRef]
- Huxley, A. Muscle Structure and Theories of Contraction. Prog. Biophys. Biophys. Chem. 1957, 7, 255–318. [Google Scholar] [CrossRef]
- Chase, P.B.; Macpherson, J.M.; Daniel, T.L. A Spatially Explicit Nanomechanical Model of the Half-Sarcomere: Myofilament Compliance Affects Ca2+ -Activation. Ann. Biomed. Eng. 2004, 32, 1559–1568. [Google Scholar] [CrossRef] [PubMed]
- Sugiura, S.; Okada, J.-I.; Washio, T.; Hisada, T. UT-Heart: A Finite Element Model Designed for the Multiscale and Multiphysics Integration of Our Knowledge on the Human Heart. In Computational Systems Biology in Medicine and Biotechnology: Methods and Protocols; Springer: New York, NY, USA, 2022; pp. 221–245. [Google Scholar]
- SILICOFCM H2020 Project: In Silico Trials for Drug Tracing the Effects of Sarcomeric Protein Mutations Leading to Familial Cardiomyopathy, 777204, 2018–2022. Available online: https://silicofcm.eu/ (accessed on 6 February 2023).
- Filipovic, N.; Saveljic, I.; Sustersic, T.; Milosevic, M.; Milicevic, B.; Simic, V.; Ivanovic, M.; Kojic, M. In Silico Clinical Trials for Cardiovascular Disease. J. Vis. Exp. 2022, e63573. [Google Scholar] [CrossRef] [PubMed]
- Filipovic, N.; Sustersic, T.; Milosevic, M.; Milicevic, B.; Simic, V.; Prodanovic, M.; Mijailovic, S.; Kojic, M. SILICOFCM Platform, Multiscale Modeling of Left Ventricle from Echocardiographic Images and Drug Influence for Cardiomyopathy Disease. Comput. Methods Programs Biomed. 2022, 227, 107194. [Google Scholar] [CrossRef] [PubMed]
- Barnoon, P.; Ashkiyan, M. Magnetic Field Generation Due to the Microwaves by an Antenna Connected to a Power Supply to Destroy Damaged Tissue in the Liver Considering Heat Control. J. Magn. Magn. Mater. 2020, 513, 167245. [Google Scholar] [CrossRef]
- Barnoon, P.; Bakhshandehfard, F. Thermal Management in a Biological Tissue in Order to Destroy Tissue under Local Heating Process. Case Stud. Therm. Eng. 2021, 26, 101105. [Google Scholar] [CrossRef]
- Chaudhary, R.K.; Kumar, D.; Rai, K.N.; Singh, J. Numerical Simulation of the Skin Tissue Subjected to Hyperthermia Treatment Using a Nonlinear DPL Model. Therm. Sci. Eng. Prog. 2022, 34, 101394. [Google Scholar] [CrossRef]
- Chaudhary, R.K.; Singh, J. Numerical Analysis of Thermal Response on a Non-Linear Model of Multi-Layer Skin under Heating and Cooling Processes. Int. Commun. Heat Mass Transf. 2022, 139, 106467. [Google Scholar] [CrossRef]
- Regazzoni, F.; Dedè, L.; Quarteroni, A. Biophysically Detailed Mathematical Models of Multiscale Cardiac Active Mechanics. PLoS Comput. Biol. 2020, 16, e1008294. [Google Scholar] [CrossRef]
- Macalino, S.J.Y.; Gosu, V.; Hong, S.; Choi, S. Role of Computer-Aided Drug Design in Modern Drug Discovery. Arch. Pharm. Res. 2015, 38, 1686–1701. [Google Scholar] [CrossRef]
- Selvaraj, C.; Chandra, I.; Singh, S.K. Artificial Intelligence and Machine Learning Approaches for Drug Design: Challenges and Opportunities for the Pharmaceutical Industries. Mol. Divers. 2022, 26, 1893–1913. [Google Scholar] [CrossRef]
- Opo, F.A.D.M.; Rahman, M.M.; Ahammad, F.; Ahmed, I.; Bhuiyan, M.A.; Asiri, A.M. Structure Based Pharmacophore Modeling, Virtual Screening, Molecular Docking and ADMET Approaches for Identification of Natural Anti-Cancer Agents Targeting XIAP Protein. Sci. Rep. 2021, 11, 4049. [Google Scholar] [CrossRef]
- BIOIRC. PAK Finite Element Software; BIOIRC: Kragujevac, Serbia, 2022. [Google Scholar]
- Filipovic, N.; Mijailovic, S.; Tsuda, A.; Kojic, M. An Implicit Algorithm within the Arbitrary Lagrangian–Eulerian Formulation for Solving Incompressible Fluid Flow with Large Boundary Motions. Comput. Methods Appl. Mech. Eng. 2006, 195, 6347–6361. [Google Scholar] [CrossRef]
- Pičulin, M.; Smole, T.; Žunkovič, B.; Kokalj, E.; Robnik-Šikonja, M.; Kukar, M.; Fotiadis, D.I.; Pezoulas, V.C.; Tachos, N.S.; Barlocco, F.; et al. Disease Progression of Hypertrophic Cardiomyopathy: Modeling Using Machine Learning. JMIR Med. Inform. 2022, 10, e30483. [Google Scholar] [CrossRef] [PubMed]
- Mijailovich, S.M.; Prodanovic, M.; Poggesi, C.; Geeves, M.A.; Regnier, M. Multiscale Modeling of Twitch Contractions in Cardiac Trabeculae. J. Gen. Physiol. 2021, 153, e202012604. [Google Scholar] [CrossRef] [PubMed]
- Prodanovic, M.; Geeves, M.A.; Poggesi, C.; Regnier, M.; Mijailovich, S.M. Effect of Myosin Isoforms on Cardiac Muscle Twitch of Mice, Rats and Humans. Int. J. Mol. Sci. 2022, 23, 1135. [Google Scholar] [CrossRef]
- Coppini, R.; Ferrantini, C.; Pioner, J.M.; Santini, L.; Wang, Z.J.; Palandri, C.; Scardigli, M.; Vitale, G.; Sacconi, L.; Stefàno, P.; et al. Electrophysiological and Contractile Effects of Disopyramide in Patients With Obstructive Hypertrophic Cardiomyopathy. JACC Basic Transl. Sci. 2019, 4, 795–813. [Google Scholar] [CrossRef]
- Morgan, J.P.; Chesebro, J.H.; Pluth, J.R.; Puga, F.J.; Schaff, H.V. Intracellular Calcium Transients in Human Working Myocardium as Detected with Aequorin. J. Am. Coll. Cardiol. 1984, 3, 410–418. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Henze, M.; Anderson, R.L.; Gong, H.; Wong, F.L.; del Rio, C.L.; Irving, T. The Super-Relaxed State and Length Dependent Activation in Porcine Myocardium. Circ. Res. 2021, 129, 617–630. [Google Scholar] [CrossRef]
- Regnier, M.; Lee, D.M.; Homsher, E. ATP Analogs and Muscle Contraction: Mechanics and Kinetics of Nucleoside Triphosphate Binding and Hydrolysis. Biophys. J. 1998, 74, 3044–3058. [Google Scholar] [CrossRef] [Green Version]
- Regnier, M.; Rivera, A.J.; Chen, Y.; Chase, P.B. 2-Deoxy-ATP Enhances Contractility of Rat Cardiac Muscle. Circ. Res. 2000, 86, 1211–1217. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; McMillen, T.S.; Childers, M.C.; Gong, H.; Regnier, M.; Irving, T. Structural OFF/ON Transitions of Myosin in Relaxed Porcine Myocardium Predict Calcium-Activated Force. Proc. Natl. Acad. Sci. USA 2023, 120, e2207615120. [Google Scholar] [CrossRef] [PubMed]
- Morgan, J. The Effects of Digitalis on Intracellular Calcium Transients in Mammalian Working Myocardium as Detected with Aequorin. J. Mol. Cell. Cardiol. 1985, 17, 1065–1075. [Google Scholar] [CrossRef] [PubMed]
- O’Hara, T.; Virág, L.; Varró, A.; Rudy, Y. Simulation of the Undiseased Human Cardiac Ventricular Action Potential: Model Formulation and Experimental Validation. PLoS Comput. Biol. 2011, 7, e1002061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zampieri, M.; Argirò, A.; Marchi, A.; Berteotti, M.; Targetti, M.; Fornaro, A.; Tomberli, A.; Stefàno, P.; Marchionni, N.; Olivotto, I. Mavacamten, a Novel Therapeutic Strategy for Obstructive Hypertrophic Cardiomyopathy. Curr. Cardiol. Rep. 2021, 23, 79. [Google Scholar] [CrossRef] [PubMed]
- Green, E.M.; Wakimoto, H.; Anderson, R.L.; Evanchik, M.J.; Gorham, J.M.; Harrison, B.C.; Henze, M.; Kawas, R.; Oslob, J.D.; Rodriguez, H.M.; et al. A Small-Molecule Inhibitor of Sarcomere Contractility Suppresses Hypertrophic Cardiomyopathy in Mice. Science 2016, 351, 617–621. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heart Failure Society of America (HFSA). U.S. Food and Drug Administration Approves CamzyosTM (Mavacamten) for the Treatment of Adults with Symptomatic New York Heart Association Class II-III Obstructive Hypertrophic Cardiomyopathy (HCM) to Improve Functional Capacity and Symptoms. Available online: https://hfsa.org/us-food-and-drug-administration-approves-camzyostm-mavacamten-treatment-adults-symptomatic-new-york (accessed on 6 February 2023).
- Hegde, S.M.; Lester, S.J.; Solomon, S.D.; Michels, M.; Elliott, P.M.; Nagueh, S.F.; Choudhury, L.; Zemanek, D.; Zwas, D.R.; Jacoby, D.; et al. Effect of Mavacamten on Echocardiographic Features in Symptomatic Patients With Obstructive Hypertrophic Cardiomyopathy. J. Am. Coll. Cardiol. 2021, 78, 2518–2532. [Google Scholar] [CrossRef] [PubMed]
- Regnier, M.; Homsher, E. The Effect of ATP Analogs on Posthydrolytic and Force Development Steps in Skinned Skeletal Muscle Fibers. Biophys. J. 1998, 74, 3059–3071. [Google Scholar] [CrossRef] [Green Version]
- Regnier, M.; Martin, H.; Barsotti, R.J.; Rivera, A.J.; Martyn, D.A.; Clemmens, E. Cross-Bridge versus Thin Filament Contributions to the Level and Rate of Force Development in Cardiac Muscle. Biophys. J. 2004, 87, 1815–1824. [Google Scholar] [CrossRef] [Green Version]
- Korte, F.S.; Dai, J.; Buckley, K.; Feest, E.R.; Adamek, N.; Geeves, M.A.; Murry, C.E.; Regnier, M. Upregulation of Cardiomyocyte Ribonucleotide Reductase Increases Intracellular 2 Deoxy-ATP, Contractility, and Relaxation. J. Mol. Cell. Cardiol. 2011, 51, 894–901. [Google Scholar] [CrossRef] [Green Version]
- Djorovic, S. Myocardial Work and Aorta Stenosis Simulation. In Cardiovascular and Respiratory Bioengineering; Elsevier: Amsterdam, The Netherlands, 2022; pp. 135–147. [Google Scholar]
- Maron, B.J.; Rowin, E.J.; Udelson, J.E.; Maron, M.S. Clinical Spectrum and Management of Heart Failure in Hypertrophic Cardiomyopathy. JACC Heart Fail. 2018, 6, 353–363. [Google Scholar] [CrossRef]
- Warriner, D.R.; Brown, A.G.; Varma, S.; Sheridan, P.J.; Lawford, P.; Hose, D.R.; Al-Mohammad, A.; Shi, Y. Closing the Loop: Modelling of Heart Failure Progression from Health to End-Stage Using a Meta-Analysis of Left Ventricular Pressure-Volume Loops. PLoS ONE 2014, 9, e114153. [Google Scholar] [CrossRef] [PubMed]

















| Patient No. | Prediction | Reliability | PredictedError | ConfidenceMin | ConfidenceMax |
|---|---|---|---|---|---|
| 1 | 0.010995677 | 0.987413164 | 0.082859018 | 0.003019494 | 0.059243858 |
| 2 | 0.082876824 | 0.965970863 | 0.144172512 | 0.019990185 | 0.165266529 |
| 3 | 0.55732954 | 0.858801931 | 0.450618253 | 0.117242657 | 0.701754749 |
| 4 | 0.027759297 | 0.980057329 | 0.103892767 | 0.004188759 | 0.077506609 |
| 5 | 0.5642663 | 0.885699762 | 0.373704863 | 0.047019321 | 0.564266324 |
| Patient No. | LVEF [%] | |||
|---|---|---|---|---|
| Clinical Value − Initial | Simulation − Initial | Clinical Value − Posterior | Simulation − Posterior | |
| 3 | 64 | 59.75 | 50 | 49.10 |
| 5 | 60 | 61.42 | 60 | 61.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomasevic, S.; Milosevic, M.; Milicevic, B.; Simic, V.; Prodanovic, M.; Mijailovich, S.M.; Filipovic, N. Computational Modeling on Drugs Effects for Left Ventricle in Cardiomyopathy Disease. Pharmaceutics 2023, 15, 793. https://doi.org/10.3390/pharmaceutics15030793
Tomasevic S, Milosevic M, Milicevic B, Simic V, Prodanovic M, Mijailovich SM, Filipovic N. Computational Modeling on Drugs Effects for Left Ventricle in Cardiomyopathy Disease. Pharmaceutics. 2023; 15(3):793. https://doi.org/10.3390/pharmaceutics15030793
Chicago/Turabian StyleTomasevic, Smiljana, Miljan Milosevic, Bogdan Milicevic, Vladimir Simic, Momcilo Prodanovic, Srboljub M. Mijailovich, and Nenad Filipovic. 2023. "Computational Modeling on Drugs Effects for Left Ventricle in Cardiomyopathy Disease" Pharmaceutics 15, no. 3: 793. https://doi.org/10.3390/pharmaceutics15030793
APA StyleTomasevic, S., Milosevic, M., Milicevic, B., Simic, V., Prodanovic, M., Mijailovich, S. M., & Filipovic, N. (2023). Computational Modeling on Drugs Effects for Left Ventricle in Cardiomyopathy Disease. Pharmaceutics, 15(3), 793. https://doi.org/10.3390/pharmaceutics15030793