A Hybrid Robust-Learning Architecture for Medical Image Segmentation with Noisy Labels

Abstract

Deep-learning models require large amounts of accurately labeled data. However, for medical image segmentation, high-quality labels rely on expert experience, and less-experienced operators provide noisy labels. How one might mitigate the negative effects caused by noisy labels for 3D medical image segmentation has not been fully investigated. In this paper, our purpose is to propose a novel hybrid robust-learning architecture to combat noisy labels for 3D medical image segmentation. Our method consists of three components. First, we focus on the noisy annotations of slices and propose a slice-level label-quality awareness method, which automatically generates label-quality scores for slices in a set. Second, we propose a shape-awareness regularization loss based on distance transform maps to introduce prior shape information and provide extra performance gains. Third, based on a re-weighting strategy, we propose an end-to-end hybrid robust-learning architecture to weaken the negative effects caused by noisy labels. Extensive experiments are performed on two representative datasets (i.e., liver segmentation and multi-organ segmentation). Our hybrid noise-robust architecture has shown competitive performance, compared to other methods. Ablation studies also demonstrate the effectiveness of slice-level label-quality awareness and a shape-awareness regularization loss for combating noisy labels.

1. Introduction

Medical image segmentation is of importance for clinical diagnosis, pathology research, and the development of treatment plans. A typical situation in the medical image field is the usage of 3D whole-volume data (e.g., CT or MRI data), where the whole volume is a set consisting of tens or hundreds of slices for every patient. With the advent of deep learning, numerous methods based on deep neural networks (DNNs) have been developed and show promising performance for medical image segmentation [1,2,3]. The success relies on the existence of an abundance of correctly labeled data. However, this assumption often does not hold for real applications. The label quality heavily depends on the experience and preferences of operators, and less-experienced annotators provide relative noisy labels. Especially for 3D medical images, the data is annotated in 2D and slice-by-slice, resulting in heavy labeling work and inconsistent quality among slices [4]. Many works have proven that low-quality annotations will degrade the performance of models and lead to some misunderstandings for subsequent computer-aided diagnoses. In this study, we aim to develop noise-robust methods for 3D medical image segmentation with noisy labels.

Recent methods for learning from noisy labels can be roughly divided as follows. First, a label transition matrix based on pre-defined knowledge is proposed to correct corresponding loss functions [5,6,7,8]. The matrix is used to learn latent noise patterns between noisy and clean annotations. However, they regard categories with clear meanings at states, which is suitable for classification tasks but cannot be directly applied to segmentation tasks. Second, some methods resort to redesigning robust loss functions instead of the conventional loss functions, such as generalized cross-entropy loss [9] and symmetric cross-entropy loss [10]. However, the effectiveness has not been verified for medical image segmentation tasks [11]. Third, many methods are proposed based on the loss re-weighting strategy, which is a very popular way to assign different weights to different samples. They make the relatively clean samples contribute more, while the relatively noisy samples contribute less for the training. The core is designing reliable criteria to estimate and select samples. For example, Mirikharaji et al. [12] proposed deploying a meta-learning framework for automatically learning the weights of pixels based on gradient directions, which was an extension of the “learning to re-weight” [13] method, from classification tasks to segmentation tasks. However, this method requires extra, trusted subsets of samples for training. Zhu et al. [14] introduced a pick-and-learn method with label-quality evaluation and an over-fitting control module. The important weights were assigned for dealing with 2D noisy-labeled image segmentation. Zhang et al. [15] proposed a tri-network by extending co-teaching [16], where they maintained three networks simultaneously for sample selection. This method can be regarded as hard-weighting. However, both the pick-and-learn and tri-network methods have been developed for 2D medical images, and cannot be directly applied for resource-intensive 3D medical image segmentation. Presently, the related investigations for 3D biomedical segmentation with low-quality noisy labels have not aroused enough attention.

In this paper, we concentrate on the problem of noisy-labeled medical image segmentation, especially for 3D medical volumetric data with tens or hundreds of slices in every whole volume. Specially, we propose a novel hybrid robust-learning architecture to combat noisy labels. First, we propose a novel slice-level label-quality awareness module (LQAM), which is jointly trained with a conventional segmentation module to predict label quality scores for each slice. Inspired by the idea of set-to-set recognition, we regard the whole volume of patients as a set of slices. By incorporating a 3D image segmentation module and a 2D LQAM, our hybrid architecture could predict label quality scores of the whole-volume slices in one shot. Second, we employ shape-awareness regularization to encourage the introduction of prior shape information. To be concrete, we apply the Hausdorff loss, based on distance transform maps, to boost the segmentation performance. Third, we construct our hybrid architecture based on the inspiration of the re-weighting strategy, which could adjust the contributions of relatively clean and noisy slices to improve the noise tolerance of the trained method. Finally, we experiment with two representative, publicly available datasets, i.e., liver segmentation and abdominal multi-organ segmentation. The results have shown the competitive performance of our noise-robust hybrid architecture. The main contributions are as follows:

(1)

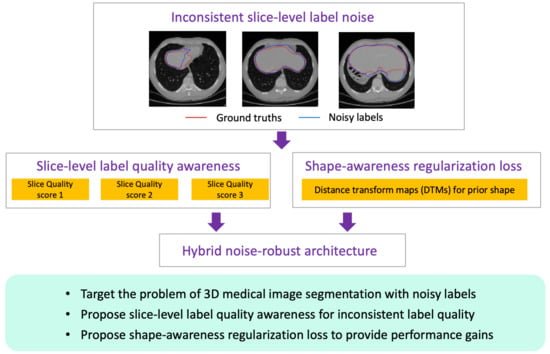
Different from previous studies, we target the challenging problem of 3D medical image segmentation with noisy labels, especially the inconsistent noisy label qualities among different slices. To address this problem, we propose a novel end-to-end hybrid robust-learning architecture to combat noisy labels from the perspective of slice-level label-quality awareness;

(2)

We propose a novel slice-level label-quality awareness method, which automatically generates quality scores for each slice in a set without knowing the prior noise distribution. With the help of re-weighting, our method can alleviate the negative effect of noisy labels. The design is particularly effective for 3D medical image segmentation by satisfying the constraints of noise tolerance and the capacity limitations of GPUs;

(3)

We propose a shape-awareness regularization loss to introduce prior shape information to provide extra performance gains. In the presence of noisy labels, we regard it as an auxiliary loss instead of the main learning targets and, further, it benefits the model training together with slice-level label-quality awareness. To our knowledge, this is the first attempt to apply prior shape information for the problem of learning with noisy labels.

2. Related Works

We review some related works for developing noise-robust methods. The representative methods can be roughly divided as follows. A label transition matrix based on pre-defined knowledge is proposed to correct the corresponding loss function. The matrix is used to learn latent noise patterns between noisy and clean annotations [17]. The key is how to accurately estimate the label transition matrix. For example, Goldberger et al. added a linear noise layer at the end of a backbone convolutional neural network to implicitly estimate the matrix [18]. Patrini et al. estimated a transition matrix by forward and backward loss-correction, which depended on strong assumptions to stack the maximum of each class [5]. Hendrycks et al. proposed gold loss-correction via mean prediction, which relied on extra, trusted subsets of data to accurately estimate the corrected matrix [6]. Wang et al. adapted a meta-learning method to directly optimize a noise transition matrix with the help of a large noisy dataset and a small trusted subset [7]. Han et al. proposed the introduction of prior knowledge for estimating a noise transition matrix [19]. As for medical applications, Dgani et al. followed the line of a noise-adaptation layer to represent the transition matrix and checked its applicability for breast microcalcification classification [8]. However, the above methods regard categories with clear meanings at states, which is suitable for classification tasks but cannot be directly applied to segmentation tasks.

Some methods focus on re-designing a robust loss function to combat noisy labels, which means they design a new robust loss function as the alternative to the conventional loss function in the presence of noisy labels. For example, Zhang and Sabuncu et al. proposed generalized cross-entropy loss [9], which combined the advantages of categorical cross-entropy and mean absolute error [20]. Wang et al. proposed a popular symmetric cross-entropy loss, which was the combination of cross-entropy and reverse cross-entropy [10]. Menon et al. leveraged gradient clipping for designing new loss functions [21]. However, these robust loss functions are developed based on their specific constraints, and the effectiveness may be reduced when encountering relatively complex medical segmentation data [11].

Some regularization methods have also been proposed to reduce the overfitting effect based on explicit or implicit forms. The former applies an explicit form to modify the training loss, such as early-learning regularization [22] or trace regularization [23]. The latter means they have the similar effect of regularization without the explicit form [24,25,26,27]. However, this kind of method should be designed with specific characteristics or it should introduce sensitive model-dependent hyperparameters.

Some methods are proposed based on the idea of loss re-weighting. Here, they make the relatively clean samples contribute more, while the relatively noisy samples contribute less for the training. The core of this method is how to design the accurate criterion to estimate and select samples. For example, Jiang et al. trained a mentor network to guide a student network by assigning weights to samples [28]. Arazo et al. calculated sample weights by modeling losses per-sample with a mixture model [29]. Han et al. used multiple class prototypes to assign attention weights to data samples [30]. Lee et al. designed an additional network to decide whether a label was noisy or not and produced the weight of each sample to reduce the influence of noisy labels [31]. Ren et al. proposed re-weighting samples based on their gradient directions and a meta-learning framework [13]. Under this investigation, Shu et al. proposed an explicit mapping method for sample weighting based on a meta-weight net [32]. However, the mentioned methods are all used for classification tasks of a natural-image domain; they cannot be directly applied to segmentation tasks, especially for 3D medical image segmentation tasks.

In fact, the research on medical image segmentation tasks with noisy labels is in its infancy. For example, Mirikharaji et al. [12] proposed deploying a meta-learning framework for automatically learning the weights of pixels based on gradient directions, which was an extension of the ”learning to re-weight” [13] method, from classification tasks to segmentation tasks. However, this method requires extra, trusted subsets of samples for training. Zhu et al. introduced a pick-and-learn method with label-quality evaluation and an over-fitting control module [14]. Then, important weights were assigned for dealing with 2D noise-labeled biomedical segmentation. Zhang et al. proposed a tri-network [15] by extending co-teaching [16], where they maintained three networks simultaneously for sample selection. This method can be regarded as hard-weighting. However, both the pick-and-learn and tri-network methods have been developed for 2D medical images, and they cannot be directly applied for resource-intensive 3D medical volumetric image segmentation. From the perspective of sample selection, Min et al. [33] proposed their two-stream networks, based on pixel-wise sample selection. They selected samples from the disagreement area, where two predictions coming from two networks were different [34]. However, this method selected pixel-wise samples and was not suitable for estimating the quality of every slice. Presently, the related investigations for 3D biomedical segmentation with low-quality noisy labels has not aroused enough attention. In this paper, we target the problem of noisy labeled 3D medical organ segmentation. In particular, we focus on the inconsistent noisy labeled slices among the whole volume. After obtaining the quality-awareness scores of slices, we further propose our hybrid noise-tolerance architecture with the help ofa re-weighting strategy, which is different from previous works.

3. Methods

We aim to develop a hybrid architecture to weaken the negative effect of noisy labels. This architecture could automatically estimate the label quality of slices without extra clean labels. As shown in Figure 1, the novel hybrid framework contains four major modules: (1) a 3D segmentation module, which generates whole-volume segmentation probability maps in one shot; (2) a 2D slice-level label-quality awareness module, which predicts label quality scores for each slice; (3) a shape-awareness regularization loss for introducing prior information; (4) a final re-weighting module, which assigns different weights for different slices to construct the final loss.

3.1. Segmentation Module

Considering the complementary relationship among slices of CT (or MRI) data, we prefer to choose the 3D neural network as the basic segmentation module to leverage the spatial relationship between slices, instead of the 2D segmentation model. Considering the promising performance of U-net, we select 3D U-net as the backbone [35], which has proven its effectiveness for 3D volumetric images. Further, we extend our backbone with two important modules. First, we adopt a residual skip connection for each convolutional block to aid the total training [36]. Second, we introduce 3D squeeze-and-excitation (SE) blocks for better feature representation. Inspired by the recent proposed 2D SE module for image classification [37], we introduce the 3D extension for our image segmentation.

3.2. Label-Quality Awareness Module

A label-quality awareness module (LQAM) is proposed to automatically learn the quality of labels among slices, thus reducing the impact of noisy labels with the re-weighting strategy. Considering that the slices that belong to the whole volume are annotated slice-by-slice and in 2D by less-experienced operators, the label quality of slices may be noisy and inconsistent. We regard the whole-volume data as the set of slices, and the quality scores of slices as another set.

In this section, we design our label-quality awareness module to estimate label quality of slices. The set $S=\{I_1,I_2,\dots ,I_N\}$ is used to denote the set of slices with different label qualities, which can be compared with each other. We use $I_i$ to denote the information of the i-th slice and use N to represent the number of slices belonging to one volume. Let $Q\left(S\right)$ denote the set of quality scores belonging to the whole -volume, satisfying:

$$Q\left(S\right)=F(I_1,I_2,\dots ,I_N),$$

(1)

where $F(·)$ is the quality-awareness function. The challenge is to find an optimized $F(·)$, which aggregates features from the whole volumetric set to obtain different quality scores. As neural networks could approximate various functions, we obtain the quality scores via neural network learning [30,38]. The notion is that images with higher-quality labeled information are easier to recognize, while lower-quality labeled information are hard to fit. This is related to the memorization of neural networks, and has been widely used for the recognition of noisy labels in existing natural image classification tasks with noisy labels [39]. We also use this trick to estimate the label quality of the slice set. More specifically, the slices with noisy labels have relatively higher losses, while the slices with well-annotated labels have relatively smaller losses during the training process. Therefore, with the help of losses coming from the main segmentation network, the LQAM could assess the relative quality of every slice.

We construct our label-quality awareness module using deep neural networks, which are trained together with a main segmentation network. We focus on learning with noisy labels where the images are intact and the labels are noisy. As for the input information to the LQAM, we use the set $S=\{I_1,I_2,\dots ,I_N\}$. In order to deal with noisy labels, the concatenations of image, foreground, and background are used as the whole input information $I_i$ of the i-th slice. We use these three components to contain enough information about noisy labels, which is used for subsequent label-quality awareness. Moreover, the LQAM module is jointly trained with the main segmentation. We only use this kind of concatenation as the input to keep the number of parameters constant, regardless of the number of organs. This construction is very helpful for satisfying the memory limitations of GPUs [40], and is appliable for resource-intensive volumetric segmentation. After obtaining the label quality scores of slices, the segmentation loss could be adjusted to combat noisy labels. With the main segmentation network and the label-quality awareness network, we construct our hybrid noise-robust architecture in Section 3.4.

3.3. Shape-Awareness Regularization Loss

We attempt to investigate the method for considering prior shape information to provide extra performance gains. Instead of using the complex techniques that require computationally expensive optimizations, we resort to the distance transform maps (DTMs), which have been investigated for introducing shape information for segmentation tasks [41,42]. In their studies, the segmentation labels are clean and provide accurate supervision information. However, in our study, the labels are noisy and the supervision signals are confusing. If directly applying the DTMs as the learning targets, as with the representative works [41,42], it will lead to unstable training or severe overfitting problems. There are no related studies to apply DTMs for the tasks of learning with noisy labels. In order to benefit from the shape information and exclude the negative effect of noisy labels, we propose shape-awareness regularization loss as the auxiliary loss, which is very different from previous studies.

Inspired by the studies of [41,42], our regularization loss $L_R$ is formulated as:

$$L_R=\frac{1}{\left|\mathrm{\Omega }\right|}\sum _{\mathrm{\Omega }}{(P-G)}^2\circ (G_{DTM}^2+P_{DTM}^2),$$

(2)

where G denotes the original labels and contains noise. P means the outputs of predictions. $G_{DTM}$ and $P_{DTM}$ denote the DTMs of original labels G and predictions P. Let $\mathrm{\Omega }$ denote the grid on which the slice is defined. Formally, the $DTM$ of G is written as:

$$G_{DTM}=\left\{\begin{array}{cc}\underset{y\in \partial G}{inf}\left|\right|v-{y\left|\right|}_2,\hfill & v\in G_{in};\hfill \\ 0,\hfill & others\hfill \end{array}\right.,$$

(3)

where $\left|\right|v-{y\left|\right|}_2$ is the Euclidian distance between voxels v and y, and $G_{in}$ denotes the inside of the object. $G_{DTM}$ computes the distance transformation of the foreground and the presentation for $P_{DTM}$ is similar. We further normalize the $G_{DTM}$ to be in the range $(-1,1)$ by dividing the maximum value. As an implicit shape representation, DTMs embed contours in a higher dimensional space. With the aid of slice-level label-quality awareness, the regularization loss is useful for boosting the final segmentation performance.

3.4. The Final Framework

We apply the idea of re-weighting to develop the final framework, which makes relatively clean samples contribute more to the training and compresses the influence of relatively noisy samples. We construct our total loss consisting of two parts. The first one $L_{seg}$ is the cross-entropy loss, which is calculated with prediction maps and the original labels. The second one $L_R$ is defined as the shape-awareness regularization loss. The final re-weighted loss $L_{final}$ is:

$$L_{final}=Q_{LQAM}{(L}_{seg}+\lambda L_R),$$

(4)

where $Q_{LQAM}$ are the quality weights originating from the LQAM. $\lambda$ is the hyper-parameter. Our method is independent of an auxiliary clean dataset or prior information about noise distribution, which is more applicable for 3D biomedical segmentation tasks.

4. Experiments and Results

4.1. Data and Implementation Details

We experiment with the publicly available medical dataset “Chaos” to justify the performance of our hybrid robust framework. The Chaos challenges have been held in The IEEE international Symposium on Biomedical Imaging (ISBI) 2019 and contain CT and MRI datasets. More details about the original data descriptions and data acquisition can be found in [43]. We choose CT data for liver segmentation and MRI data for abdominal multi-organ segmentation (i.e., liver, right kidney, left kidney and spleen). Each volume in these two datasets corresponds to a series of DICOM images belonging to a single patient. The CT dataset consists of 20 different patients and is divided into training (12 patients) and testing (8 patients) in experiments. For the MRI dataset, we choose T2-SPIR (20 patients). We divide the 12 cases for training and the remaining 8 cases for testing. We resize the CT images as $64\times 196\times 196$ and resize the MRI images as $32\times 196\times 196$. We clip all values larger than 2000 as 2000, and then pre-process the data by normalization.

As both the CT dataset and the MRI dataset have clean labels, we first generate noisy labeled images under different noise settings. Following the previous works of [14,15], we set the number of slices selected for noise generation as the noise rate, and set the morphological changes within pixels for every selected slice as the noise level. For example, we set the noise rate to 50% and noise level to 1–8 pixels, which means we randomly select 50% of the slices from the whole volume and further erode or dilate every selected slice with 1–8 pixels.

We utilize PyTorch for realizing our experiments. The learning rate is set empirically to 0.001. The Adam optimizer is used for optimization and the Betas of the optimizer are set to 0.9 and 0.999. We set the maximum epoch as 10,000 in the experiments. We repeat the experiments three times and report the average for the final performance. During training, we select 3D SE ResUnet as the backbone with four residual and SE blocks. The backbone consists of a contracting path and an expanding path. We prefer the contracting path as the LQAM module. During training, the batch size for the 3D segmentation model is set to 1, which means we obtain all predictions belonging to a patient in one shot. We use the widely used metric of dice score to measure the segmentation performance. $\lambda$ is set to 0.01 for the experiments.

As for the network architecture, we use 3D Unet as the basic backbone, with residual blocks and SE blocks. We expand the 2D squeeze, excitation, scale, and convolutional functions to obtain the 3D SE counterparts. The encoder consists of four residual modules with 16, 32, 32, and 64 output channels, followed by a down-sampling layer. The decoder shares the symmetric structure, but with up-sampling layers. For each residual module, we use two $3\times 3\times 3$ convolution blocks, two SE modules, and corresponding up-sampling or down-sampling layers. The down-sampling layer is achieved via 3D max-pooling with stride 2 and the up-sampling is achieved with the strategy of nearest neighbor. Each convolution block consists of convolutional layers, an ELU activation function, and a 3D batch-normalization layer. We prefer the contracting path as the LQAM module.

4.2. Comparisons on Liver Segmentation Dataset

We conduct experiments on a liver segmentation benchmark to demonstrate the effectiveness of our hybrid robust architecture. The dataset has 3D CT images. We train our network on the noisy-labeled data under different noise settings and test the network with clean-labeled data. Specifically, we set two noise levels (noise level 1 of 1–8 pixels and noise level 2 of 5–18 pixels) and three noise rates (noise rate = 25%, 50%, and 75%). Following the generation process of noisy labels [14,15], we obtain the data with simulated noisy labels.

The comparing baselines include: (1) Plain [35]: the conventional training based on a 3D segmentation model with noisy labels. We use 3D U-net with the additions of residual blocks and 3D SE blocks as the backbone. (2) Pick-and-learn [14]: a representative method for addressing 2D medical image segmentation with noisy labels. We regard every slice as a 2D datum and further adopt the pick-and-learn strategy for the corresponding robust learning. (3) Disagreement [33]: a noise-robust method from the perspective of sample selection, which selects pixels from the disagreement area to obtain informative samples. (4) Area-aware method proposed by [44]: the area aware-factor is calculated as the ratio between the area of the foreground and the area of the background, and is then introduced by a simple multiplication strategy. (5) INT [45]: this method aims to distill effective supervision information from image-level data to develop a noise-tolerance algorithm.

The experimental results on the liver segmentation dataset with simulated noisy labels are illustrated in

Table 1. Results on the CT dataset for liver segmentation under different noise settings. We report the mean value (±std) of the dice score (%) with 3 runs.

Method	Noise Level 1			Noise Level 2
	25%	50%	75%	25%	50%	75%
Plain [35]	70.94 ± 0.96	68.97 ± 0.43	65.24 ± 1.32	59.61 ± 0.41	56.82 ± 0.19	48.07 ± 2.38
Pick-and-learn [14]	65.67 ± 0.44	59.36 ± 0.73	54.10 ± 0.86	50.91 ± 0.59	47.31 ± 0.26	40.32 ± 0.45
Disagreement [33]	71.43 ± 1.10	69.88 ± 0.24	67.58 ± 0.28	66.64 ± 0.07	55.72 ± 0.19	47.23 ± 0.25
INT [45]	77.34 ± 0.14	75.33 ± 0.08	71.67 ± 0.06	70.38 ± 0.81	60.80 ± 0.64	53.56 ± 0.67
Area-aware [44]	76.62 ± 1.75	74.92 ± 1.27	69.45 ± 1.96	70.63 ± 1.32	60.44 ± 1.98	54.82 ± 1.56
Ours	78.31 ± 0.46	76.29 ± 0.63	72.78 ± 0.60	71.72 ± 0.18	64.05 ± 0.30	56.99 ± 0.66

. On the clean-annotated dataset, we have the performance upper as the dice value of 88.55. However, the liver segmentation performance for the Plain baseline decreases sharply when adding different noise rates (from no noise to 25%, 50%, and 75%) and noise levels (from noise level 1 of 1–8 pixels to noise level 2 of 5–18 pixels). Comparing with other baselines, we could observe that our proposed hybrid architecture has a consistent performance improvement. Even in the hardest case, with noise level 2 and a noise rate of 75%, our proposed method shows its robustness to noisy labels.

Comparing with pick-and-learn, our method achieves performance gains, which demonstrates that adopting a 3D network as a backbone is more appropriate because of the implicit complementary information among slices. Comparing with the disagreement method, our superior performance shows that our hybrid architecture could mine more effective information, while disagreement only selects samples from a disagreement area, resulting few samples during training. For image-level noise-robust learning, we compare an INT (image-level noise-tolerance) method with our method. The results show the improvement, which verifies the effectiveness of our method from the perspective of slice-level noise tolerance. We further observe the results of our method and the area-aware strategy, which also verifies that our slice-level label-quality awareness and regularization loss show better performance advantages.

4.3. Comparisons on Multi-Organ Segmentation Dataset

We demonstrate the experiments on an abdomen multi-organ MRI-T2SPIR dataset, and the corresponding organs include the liver, right kidney, left kidney, and spleen.

Table 2. Experimental results (dice %) for multi-organ segmentation on abdomen MRI-T2SPIR. We report the performances of the liver, right kidney, left kidney, and spleen, as well as the average values.

Noise Rates	Method	Liver	Right Kidney	Left Kidney	Spleen	Average
No noise	Plain [35]	84.20	75.13	64.93	73.66	74.48
	Plain [35]	79.36	55.09	42.88	52.51	57.46
	Pick-and-learn [14]	80.31	45.79	38.33	38.44	50.72
25%	Disagreement [33]	73.46	49.79	44.66	52.09	55.00
	INT [45]	78.93	56.63	45.66	59.14	60.09
	Area-aware [44]	75.05	52.83	54.17	51.11	58.29
	Ours	78.00	60.72	49.62	60.95	62.32
	Plain [35]	76.86	52.43	42.75	54.40	56.61
	Pick-and-learn [14]	70.36	48.87	41.26	48.55	52.26
50%	Disagreement [33]	71.37	49.87	41.26	49.55	53.01
	INT [45]	79.10	55.10	46.97	56.29	59.37
	Area-aware [44]	75.47	51.80	46.66	54.19	57.03
	Ours	80.27	54.07	47.54	60.49	61.60
	Plain [35]	75.18	56.29	41.75	52.10	56.33
	Pick-and-learn [14]	70.79	48.13	36.83	44.22	49.99
75%	Disagreement [33]	72.99	48.49	40.41	46.42	52.08
	INT [45]	76.66	50.69	47.25	57.63	58.06
	Area-aware [44]	76.47	48.99	45.12	57.20	56.94
	Ours	78.62	52.08	51.84	59.62	60.54

depicts the comparative performance of multiple methods with noise ratios of 25%, 50%, and 75% and the noise level of 1–5 pixels. The noisy labels are generated in the same way as the liver segmentation. We report the average dice value (%) of these four organs. The upper bound with the average dice value of 74.48 is acquired by training the 3D segmentation model on a clean-labeled dataset. Other results are obtained by training the model on a dataset with corrupted labels. As illustrated, our proposed hybrid architecture outperforms other methods, which demonstrates the effectiveness of our hybrid noise-robust architecture.

4.4. Ablation Study and Visualization

We also show the ablation study in Figure 2. We use “$Plain$” to denote the basic baseline, where the model is trained without any noise-robust strategy. We use “$LQAM$” to represent our hybrid architecture with only slice-level label-quality awareness. We use “$LQAM+L_R$” to denote our proposed hybrid architecture with $LQAM$ and regularization loss $L_R$. The experiments are conducted on a liver segmentation dataset with different noise rates and noise levels. Comparing $LQAM$ and $Plain$, we can observe that adding a label-quality awareness module is necessary for developing noise-robust methods. The comparisons between $LQAM$ and $LQAM+L_R$ have shown the effectiveness of introducing shape-awareness regularization loss. This may be because the shape-awareness loss will benefit from learning some boundary information. Together with the re-weighted framework, the regularization loss helps to further improve the contribution of relatively clean samples.

We visualize some slices to show the effectiveness of our hybrid noise-robust architecture in Figure 3. For the liver segmentation dataset, we randomly select slices with noise levels of 5–18 pixels and a noise rate of 25%. For multi-organ segmentation, we show the slices with a noise level of 1–5 pixels and a noise rate of 25%.

We also show some bad examples in Figure 4, where the slices are selected from multi-organ segmentation on the abdomen MRI-T2SPIR dataset. Note that the 3D whole-volume data is a set consisting of tens or hundreds of slices for every patient. The size variances of organs among different slices are very obvious, and sometimes the organs present a relatively small size on some slices. The bad case, on the left, is the example. The organ size is relatively small in this slice, and the performance is poor. We should investigate the segmentation of small organs to further improve the performance of learning with noisy labels, which is the future work. When we observe the bad case on the right, the results show that there are some overlaps among different organs based on our method. The main reason is that the boundaries of organs in medical images are usually unclear, making it more difficult to distinguish them in the presence of noisy labels. A possible solution is to introduce prior information about the relationship among organs, which has the potential to improve the segmentation performance.

5. Conclusions

We concentrate on the problem of 3D medical image segmentation with noisy labels. We present a novel noise-robust hybrid architecture to combat noisy labels. Specifically, we propose a slice-level label-quality awareness module, which is jointly trained with a conventional segmentation module to predict label quality scores for each slice. We further introduce regularization loss by distance transform maps to boost the segmentation performance. With the calculated quality scores, we apply a re-weighting strategy on the total loss to distill effective supervision information from relatively clean samples. Our architecture can be trained without knowing the prior noise distribution or the availability of an extra trusted subset. Experimental results on the publicly available medical datasets (CT for liver segmentation and MRI-T2SPIR for abdomen multi-organ segmentation) demonstrate the effectiveness of our hybrid noise-robust architecture. In the future, we will investigate the relationships of multiple organs and hard sample mining for learning with noisy labels.