Optimal Incentives for Electric Vehicles at e-Park & Ride Hub with Renewable Energy Source
Abstract
:1. Introduction
1.1. Motivation
1.2. Related Methodologies
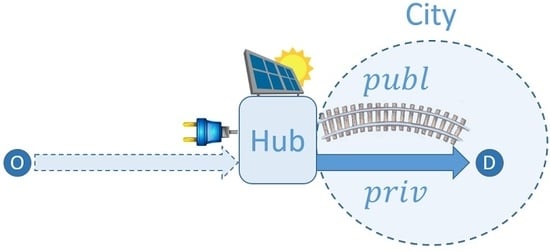
2. E-Park & Ride Hub Scenario
2.1. Route Choice
2.1.1. Model Assumptions
- Two types of vehicle are considered: an electric one (denoted EV and associated with subscript e) and a gasoline one (GV, associated with subscript g). Each commuter is associated with one of the two vehicles and the proportion of EV among them is denoted by in the model (in numerical tests, which is in line with 2035 predictions for France; see middle scenario of [1]). The proportion of GV is then given by . The choice made by all commuters between the two transport modes of Figure 1 is represented by the two variables and , which are respectively the proportions of EV and GV choosing the public transport mode. Note that the proportions of vehicles of type choosing the private transport mode may be easily deduced: .
- The decision process of commuters is assumed rational, meaning that they choose the transport mode (publ or priv) with minimal cost. Here, the costs considered are travel duration (by private or public transport), energy consumption (electricity for EV and fuel for GV) and the ticket fare (for public transport only).
2.1.2. Costs Functions
- –
- For the private mode, it depends on the total proportion (here, proportion and number of vehicles are equivalent, as the total number of vehicles is fixed) of vehicles driving downtown due to congestion effects [14] and is expressed as:where the function is the estimated travel duration on the road downtown: the higher the flow , the higher the travel duration and yields the (minimal) “free-flow” travel time. The parameters of the problem are set as follows, unless otherwise specified:
- €/h the value of time when driving, based on a French government report (http://www.strategie.gouv.fr/sites/strategie.gouv.fr/files/archives/Valeur-du-temps.pdf),
- km the length of the road, approximately the radius of Paris,
- km/h the speed limit, as in French urban areas,
- the capacity of the road, expressed in proportion of the total number of vehicles, like .
- –
- For the public transport mode linking the hub and the destination, the travel cost is assumed constant:
- €/h value of time in public transport (http://www.strategie.gouv.fr/sites/strategie.gouv.fr/files/archives/Valeur-du-temps.pdf), which is perceived by commuters as less comfortable than personal vehicles,
- min constant travel time of public transport, which was chosen equal to the free flow travel time of the private mode. Indeed, there exist reserved pathways for public transportation in several cities like Paris, so that congestion can be considered as marginal.
The duration cost of the public mode is then equal to the fixed value € and is higher than the free flow cost of the private mode. This induces trade-off decisions for vehicles between both strategies.
- is the total distance driven by the vehicles which have chosen transport mode r, and is equal to:
- –
- km distance between the origin and the hub, so that the two-way trip between origin and destination is 30 km, the daily average individual driving distance in France (following Enquête Nationale Transports et Déplacements: https://utp.fr/system/files/Publications/UTP_NoteInfo1103_Enseignements_ENTD2008.pdf), 2008, in French),
- –
- km,
- is the electricity or fuel consumed per distance unit and is supposed constant (e.g., it does not depend on speed profiles):
- –
- kWh/km, following [16],
- –
- L/km (Liter/km),
- is the charging/fueling unit price:
- –
- For EV, the key distinction made here is that it depends on the transport mode chosen.Public mode: At the hub, this charging unit price will depend on the total charging need , proportional to the number of EV parked in the hub: for example, if there are few EV at the hub ( close to 0), there is enough electricity produced at the hub to provide the charging need of these EV. This price is obtained by solving a charging problem, which is detailed in the next section.Private mode: Downtown, there is a standard constant electricity fare 40 c€/kWh, which corresponds to the electricity unit price in France (15 c€/kWh) with an additional cost (25 c€/kWh) meant for the charging operation.
- –
- €/L is considered constant.
2.2. Hub Charging Operation
2.2.1. Charging Scenario
2.2.2. Modeling of Charging Problem
Aggregated Charging Need
Temporal Charging Scheduling
Photovoltaic Production
Cost/Impact on the Local Electrical Grid
Charging Problem and Solution
- If the aggregated charging need verifies , any charging profile below the PV production is optimal, since the associated cost is zero.
- If (which corresponds to the charging need of 29 EV), the optimal scheduling has to perfectly match the production.
- If , all PV production is consumed and the remaining charging need has to be equally shared between all time slots such that the net load taken from the grid is constant.
3. Numerical Experiments
3.1. Wardrop Equilibrium Representation
3.2. Equilibrium Sensitivity to Parameters of the Problem
3.3. Optimal Solar Panel Surface
- I the initial Investment cost in solar panels, with 750 €/kWp for a solar park of the order of magnitude of 1 MWp,
- C the daily grid Costs (associated with the electricity bought from the grid), defined in Equation (8),
- R the daily Revenues from EV charging at the hub which are, by definition of the charging unit price :with the proportion of EV at the hub at equilibrium corresponding to and the total charging need , defined in Equation (4).
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Réseau de Transport d’Électricité. Bilan prévisionnel de l’équilibre offre-demande d’électricité en France - Édition 2017; Technical Report; RTE: Donnybrook, Ireland, 2018. (In French) [Google Scholar]
- Jacquot, P.; Beaude, O.; Gaubert, S.; Oudjane, N. Analysis and Implementation of an Hourly Billing Mechanism for Demand Response Management. IEEE Trans. Smart Grid 2018, 10, 4265–4278. [Google Scholar] [CrossRef]
- Beaude, O.; Lasaulce, S.; Hennebel, M.; Mohand, I. Reducing the Impact of EV Charging Operations on the Distribution Network. IEEE Trans. Smart Grid 2016, 7, 2666–2679. [Google Scholar] [CrossRef]
- Brenna, M.; Falvo, M.; Foiadelli, F.; Martirano, L.; Massaro, F.; Poli, D.; Vaccaro, A. Challenges in energy systems for the smart-cities of the future. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition, Florence, Italy, 9–12 September 2012; pp. 755–762. [Google Scholar]
- Tan, J.; Wang, L. Real-time charging navigation of electric vehicles to fast charging stations: A hierarchical game approach. IEEE Trans. Smart Grid 2017, 8, 846–856. [Google Scholar] [CrossRef]
- Wei, W.; Mei, S.; Wu, L.; Shahidehpour, M.; Fang, Y. Optimal traffic-power flow in urban electrified transportation networks. IEEE Trans. Smart Grid 2017, 8, 84–95. [Google Scholar] [CrossRef]
- Sheffi, Y. Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Methods; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1985. [Google Scholar]
- Jiang, N.; Xie, C. Computing and analysing mixed equilibrium network flows with gasoline and electric vehicles. Comput. Aided Civ. Infra. Eng. 2014, 29, 626–641. [Google Scholar]
- Altman, E.; Kameda, H. Equilibria for Multiclass Routing Problems in Multi-Agent Networks. Dyn. Games Appl. 2005, 7, 343–367. [Google Scholar]
- Mohsenian-Rad, A.H.; Wong, V.W.; Jatskevich, J.; Schober, R.; Leon-Garcia, A. Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid. IEEE Trans. Smart Grid 2010, 1, 320–331. [Google Scholar] [CrossRef]
- Alizadeh, M.; Wai, H.; Chowdhury, M.; Goldsmith, A.; Scaglione, A.; Javidi, T. Optimal Pricing to Manage Electric Vehicles in Coupled Power and Transportation Networks. IEEE Trans. Control Netw. Syst. 2017, 4, 863–875. [Google Scholar] [CrossRef]
- Wei, W.; Wu, L.; Wang, J.; Mei, S. Network Equilibrium of Coupled Transportation and Power Distribution Systems. IEEE Trans. Smart Grid 2018, 9, 6764–6779. [Google Scholar] [CrossRef]
- Sohet, B.; Beaude, O.; Hayel, Y. Routing game with nonseparable costs for EV driving and charging incentive design. In NETwork Games Control and Optimization; Birkhäuser: New York, NY, USA, 2018. [Google Scholar]
- Spiess, H. Technical note—Conical volume-delay functions. Transp. Sci. 1990, 24, 153–158. [Google Scholar] [CrossRef]
- Sétra. Fonctions Temps-débit sur les Autoroutes Interurbaines—Détermination du Coefficient D’équivalence et de la Capacité à Partir des Observations Locales. 2001. Available online: http://dtrf.setra.fr/pdf/pj/Dtrf/0002/Dtrf-0002996/DT2996.pdf?openerPage=notice (accessed on 30 October 2019).
- Fontana, M.W. Optimal Routes for Electric Vehicles Facing Uncertainty, Congestion, and Energy Constraints. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2013. [Google Scholar]
- Wardrop, J. Some theoretical aspects of road traffic research. Proc. Inst. Civ. Eng. Part II 1952, 1, 325–378. [Google Scholar] [CrossRef]
- Jacquot, P.; Beaude, O.; Benchimol, P.; Gaubert, S.; Oudjane, N. A Privacy-preserving Disaggregation Algorithm for Non-intrusive Management of Flexible Energy. arXiv 2019, arXiv:1903.03053. [Google Scholar]
- Pfenninger, S.; Staffell, I. Long-term patterns of European PV output using 30 years of validated hourly reanalysis and satellite data. Energy 2016, 114, 1251–1265. [Google Scholar] [CrossRef] [Green Version]











| Total Costs | Public Transport Mode | Private Transport Mode |
|---|---|---|
| EV | ||
| GV |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sohet, B.; Beaude, O.; Hayel, Y.; Jeandin, A. Optimal Incentives for Electric Vehicles at e-Park & Ride Hub with Renewable Energy Source. World Electr. Veh. J. 2019, 10, 70. https://doi.org/10.3390/wevj10040070
Sohet B, Beaude O, Hayel Y, Jeandin A. Optimal Incentives for Electric Vehicles at e-Park & Ride Hub with Renewable Energy Source. World Electric Vehicle Journal. 2019; 10(4):70. https://doi.org/10.3390/wevj10040070
Chicago/Turabian StyleSohet, Benoît, Olivier Beaude, Yezekael Hayel, and Alban Jeandin. 2019. "Optimal Incentives for Electric Vehicles at e-Park & Ride Hub with Renewable Energy Source" World Electric Vehicle Journal 10, no. 4: 70. https://doi.org/10.3390/wevj10040070
APA StyleSohet, B., Beaude, O., Hayel, Y., & Jeandin, A. (2019). Optimal Incentives for Electric Vehicles at e-Park & Ride Hub with Renewable Energy Source. World Electric Vehicle Journal, 10(4), 70. https://doi.org/10.3390/wevj10040070