Predicting Model for Air Transport Demand under Uncertainties Based on Particle Filter
Abstract
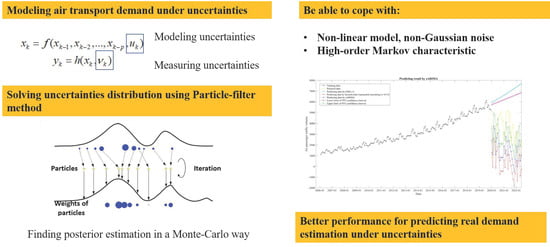
:1. Introduction
2. Modeling Approaches
2.1. Particle-Filter Based Predicting Framework
2.2. Seasonal Autoregressive Integrated Moving Average (sARIMA) Model
2.3. The Proposed sARIMA-Pf Method
2.4. Error Calculation
3. Case Study
3.1. The Predicting Scenario and the Uncertainties Modeling
3.2. Case Study of Air Passenger Traffic Volume Prediction
3.3. Case Study of Air Passenger Traffic Volume Prediction under the Pandemic Scenario
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.; de Groot, M.; Bäck, T. Using forecasting to evaluate the impact of COVID-19 on passenger air transport demand. Decis. Sci. 2021, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Kitsou, S.P.; Koutsoukis, N.S.; Chountalas, P.; Rachaniotis, N.P. International Passenger Traffic at the Hellenic Airports: Impact of the COVID-19 Pandemic and Mid-Term Forecasting. Aerospace 2022, 9, 143. [Google Scholar] [CrossRef]
- National Academies of Sciences. Engineering, and Medicine. Addressing Uncertainty about Future Airport Activity Levels in Airport Decision Making. 2012. Available online: https://nap.nationalacademies.org/catalog/22704/addressing-uncertainty-about-future-airport-activity-levels-in-airport-decision-making (accessed on 22 March 2022).
- Spitz, W.; Golaszewski, R. Airport Aviation Activity Forecasting; Transportation Research Board: Washington, DC, USA, 2007. [Google Scholar]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Williams, B.M.; Durvasula, P.K.; Brown, D.E. Urban freeway traffic flow prediction: Application of seasonal autoregressive integrated moving average and exponential smoothing models. Transp. Res. Rec. 1998, 1644, 132–141. [Google Scholar] [CrossRef]
- Andreoni, A.; Postorino, M.N. A multivariate ARIMA model to forecast air transport demand. Proc. Assoc. Eur. Transp. Contrib. 2006, 1–14. [Google Scholar]
- Tsui WH, K.; Balli, H.O.; Gilbey, A.; Gow, H. Forecasting of Hong Kong airport’s passenger throughput. Tour. Manag. 2014, 42, 62–76. [Google Scholar] [CrossRef]
- Barczak, A.; Dembińska, I.; Rozmus, D.; Szopik-Depczyńska, K. The Impact of COVID-19 Pandemic on Air Transport Passenger Markets-Implications for Selected EU Airports Based on Time Series Models Analysis. Sustainability 2022, 14, 4345. [Google Scholar] [CrossRef]
- Zhu, X.; Lin, Y.; He, Y.; Tsui, K.-L.; Chan, P.W.; Li, L. Short-Term Nationwide Airport Throughput Prediction With Graph Attention Recurrent Neural Network. Front. Artif. Intell. 2022, 105. [Google Scholar] [CrossRef] [PubMed]
- Utku, A.; Kaya, S.K. Multi-layer perceptron based transfer passenger flow prediction in Istanbul transportation system. Decis. Mak. Appl. Manag. Eng. 2022, 5, 208–224. [Google Scholar] [CrossRef]
- Lin, G.; Lin, A.; Gu, D. Using support vector regression and K-nearest neighbors for short-term traffic flow prediction based on maximal information coefficient. Inf. Sci. 2022, 608, 517–531. [Google Scholar] [CrossRef]
- Jin, F.; Li, Y.; Sun, S.; Li, H. Forecasting air passenger demand with a new hybrid ensemble approach. J. Air Transp. Manag. 2020, 83, 101744. [Google Scholar] [CrossRef]
- Wong, H.L. Time series forecasting with stochastic Markov models based on fuzzy set and grey theory. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2015; pp. 975–978. [Google Scholar]
- Meng, H.; Geng, M.; Xing, J.; Zio, E. A hybrid method for prognostics of lithium-ion batteries capacity considering regeneration phenomena. Energy 2022, 261, 125278. [Google Scholar] [CrossRef]
- Song, W.; Wang, Z.; Li, Z.; Han, Q.-L. Particle-Filter-Based State Estimation for Delayed Artificial Neural Networks: When Probabilistic Saturation Constraints Meet Redundant Channels. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Wang, S.; Zio, E.; Shi, J.; Ma, Z. A numerical approach for predicting the remaining useful life of an aviation hydraulic pump based on monitoring abrasive debris generation. Mech. Syst. Signal Process. 2020, 136, 106519. [Google Scholar] [CrossRef]
- Tongyang, L.; Shaoping, W.; Jian, S.; Zhonghai, M. An adaptive-order particle filter for remaining useful life prediction of aviation piston pumps. Chin. J. Aeronaut. 2018, 31, 941–948. [Google Scholar]
- Chen, J.; Ma, C.; Song, D.; Xu, B. Failure prognosis of multiple uncertainty system based on Kalman filter and its application to aircraft fuel system. Adv. Mech. Eng. 2016, 8, 1687814016671445. [Google Scholar] [CrossRef] [Green Version]
- Zio, E.; Peloni, G. Particle filtering prognostic estimation of the remaining useful life of nonlinear components. Reliab. Eng. Syst. Saf. 2011, 96, 403–409. [Google Scholar] [CrossRef]
- Hassani, S. Dirac delta function. In Mathematical Methods; Springer: Berlin, Germany, 2009; pp. 139–170. [Google Scholar]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. 8.9 Seasonal ARIMA models. Forecast. Princ. Practice. Otexts. Retrieved 2015, 19. [Google Scholar]
- Schneider, R.; Chen, X. Predicting Flight Demand under Uncertainty. KSCE J. Civ. Eng. 2020, 24, 635–646. [Google Scholar] [CrossRef]
- McLeod, A.I. Parsimony, Model Adequacy and Periodic Correlation in Time Series Forecasting; International Statistical Institute: The Hague, The Netherlands, 1993; pp. 387–393. [Google Scholar]










| Model | AIC | BIC | Model | AIC | BIC |
|---|---|---|---|---|---|
| ARIMA(1,1,1) | 1.9040 | 1.9131 | ARIMA(3,1,1) | 1.9052 | 1.9203 |
| ARIMA(1,1,2) | 1.8971 | 1.9093 | ARIMA(3,1,2) | 1.9072 | 1.9254 |
| ARIMA(1,1,3) | 1.9058 | 1.9210 | ARIMA(3,1,3) | 1.9086 | 1.9298 |
| ARIMA(1,1,4) | 1.9061 | 1.9243 | ARIMA(3,1,4) | 1.8900 | 1.9142 |
| ARIMA(2,1,1) | 1.9040 | 1.9161 | ARIMA(4,1,1) | 1.9049 | 1.9232 |
| ARIMA(2,1,2) | 1.9048 | 1.9200 | ARIMA(4,1,2) | 1.8994 | 1.9207 |
| ARIMA(2,1,3) | 1.8996 | 1.9178 | ARIMA(4,1,3) | 1.8964 | 1.9207 |
| ARIMA(2,1,4) | 1.8997 | 1.9210 | ARIMA(4,1,4) | 1.8909 | 1.9183 |
| Model | MSE | RMSE |
|---|---|---|
| GM(1,1) | 62,166 | 249.3309 |
| Second-order exponential smoothing with | 513,140 | 716.3373 |
| sARIMA | 111,850 | 334.4425 |
| sARIMA-pf | 28,759 | 169.5857 |
| Model | MSE | RMSE |
|---|---|---|
| GM(1,1) | 14,940,000 | 3865.3 |
| Second-order exponential smoothing with | 11,395,000 | 3375.6 |
| sARIMA-pf | 295,030 | 543.1681 |
| sARIMA-target time | 1,606,400 | 1267.4 |
| sARIMA-step-by-step | 973,740 | 986.7838 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Wu, J. Predicting Model for Air Transport Demand under Uncertainties Based on Particle Filter. Sustainability 2022, 14, 16694. https://doi.org/10.3390/su142416694
Chen B, Wu J. Predicting Model for Air Transport Demand under Uncertainties Based on Particle Filter. Sustainability. 2022; 14(24):16694. https://doi.org/10.3390/su142416694
Chicago/Turabian StyleChen, Bin, and Jin Wu. 2022. "Predicting Model for Air Transport Demand under Uncertainties Based on Particle Filter" Sustainability 14, no. 24: 16694. https://doi.org/10.3390/su142416694
APA StyleChen, B., & Wu, J. (2022). Predicting Model for Air Transport Demand under Uncertainties Based on Particle Filter. Sustainability, 14(24), 16694. https://doi.org/10.3390/su142416694