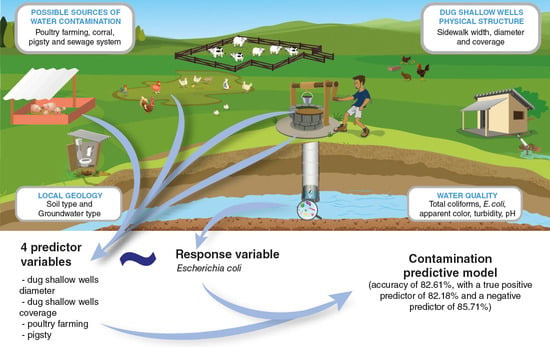
A Contamination Predictive Model for Escherichia coli in Rural Communities Dug Shallow Wells
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection
2.3. Predictor Variables Initial Selection
2.4. Model Proposal
2.5. Model Validation and Performance
3. Results
3.1. Model Proposal
3.1.1. Initial Model
3.1.2. Intermediate Model
3.1.3. Final Model
3.2. Model Validation
4. Discussion
5. Conclusions
- Shallow well diameter, the paving around it, the presence of pigsties and poultry farming were the predictors that best described (or explained) dug shallow well water contamination;
- For the final model, the pavement in the contour region had a negative relationship with the chance of water contamination of dug shallow wells (OR < 1), and, consequently, there was a probability reduction of water contamination with larger sidewalks, while the well width had a positive relationship (OR > 1), the chance of water contamination was greater in wells with larger diameters when compared to dug shallow wells with small diameters;
- Paving around dug shallow wells can help protect water coming from the well;
- Rearing pigs and chickens in the peridomicile can harm the quality of the dug shallow wells water;
- The final model showed excellent accuracy in prediction assertiveness.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vasconcelos, M.B. What are wells? Overview of the terms used to groundwater abstraction. Águas Subterrâneas 2017, 31, 44–57. [Google Scholar] [CrossRef] [Green Version]
- Suhogusoff, A.V.; Hirata, R.; Ferrari, L.C.K.M. Water quality and risk assessment of dug wells: A case study for a poor community in the city of São Paulo, Brazil. Environ. Earth Sci. 2013, 68, 899–910. [Google Scholar] [CrossRef]
- Ocheli, A.; Otuya, O.B.; Umayah, S.O. Appraising the risk level of physicochemical and bacteriological twin contaminants of water resources in part of the western Niger Delta region. Environ. Monit. Assess. 2020, 192, 324–339. [Google Scholar] [CrossRef] [PubMed]
- Braimah, J.A.; Yirenya-Tawiah, D.R.; Gordon, C. Hand-dug Well Water Quality: The Case of Two Peri-Urban Communities in Ghana. West Afr. J. Appl. Ecol. 2021, 29, 24–34. [Google Scholar]
- Casey, F.X.M.; Hakk, H.; Desutter, T.M. Free and conjugated estrogens detections in drainage tiles and wells beneath fields receiving swine manure slurry. Environ. Pollut. 2020, 256, 113384. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.Z.; Zou, H.Y.; Wu, D.L.; Chen, S.; He, L.Y.; Zhang, M.; Bai, H.; Ying, G.G. Swine farming elevated the proliferation of Acinetobacter with the prevalence of antibiotic resistance genes in the groundwater. Environ. Intern. 2020, 136, 105484. [Google Scholar] [CrossRef]
- Santos, C.E.; Medeiros, R.C.; Mancurso, M.A. Groundwater from rural wells in frederico westphalen: Quality, environmental aspects and legal compliance. An. Do Inst. De Geocienc. 2020, 43, 330–340. [Google Scholar] [CrossRef]
- Borchardt, M.A.; Stokdyk, J.P.; Kieke, B.A.; Muldoon, M.A.; Spencer, S.K.; Firnstahl, A.D.; Bonness, D.E.; Hunt, R.J.; Burch, T.R. Sources and risk factors for nitrate and microbial contamination of private household wells in the fractured dolomite aquifer of Northeastern Wisconsin. Environ. Health Perspect. 2021, 129, 067004. [Google Scholar] [CrossRef]
- Wendee, N. Farm to faucet Agricultural waste and private well contamination in Kewaunee county, Wisconsin. Environ. Health Perspect. 2021, 129, 11401. [Google Scholar] [CrossRef]
- Cherry, J.L. Recent Genetic Changes Affecting Enterohemorrhagic Escherichia coli Causing Recurrent Outbreaks. Microbiol. Spectr. 2022, 10, e00501-22. [Google Scholar] [CrossRef]
- Abioye, O.M.; Adeniran, K.A.; Abadunmi, T. Poultry Wastes Effect on Water Quality of Shallow Wells of Farms in Two Locations of Kwara State, Nigeria. Nat. Environ. Pollut. Technol. 2022, 21, 303–308. [Google Scholar] [CrossRef]
- Lwimbo, Z.D.; Komakech, H.C.; Muzuka, A.N.N. Impacts of Emerging Agricultural Practices on Groundwater Quality in Kahe Catchment, Tanzania. Water 2019, 11, 2263. [Google Scholar] [CrossRef] [Green Version]
- Nyilitya, B.; Mureithi, S.; Boeckx, P. Tracking Sources and Fate of Groundwater Nitrate in Kisumu City and Kano Plains, Kenya. Water 2020, 12, 401. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, C.; Checkley, S.; Chui, L.; Otto, S.; Neumann, N. Evaluating the risks associated with shiga-toxin-producing Escherichia coli (Stec) in private well waters in Canada. Can. J. Microbiol. 2020, 33, 337–350. [Google Scholar] [CrossRef] [PubMed]
- Burch, T.R.; Stokdyk, J.P.; Arroz, N.; Andersonanita, C.; Walshjames, F.D.; Spencer, S.K.; Firstahl, A.D.; Borchardt, M.A. Statewide Quantitative Microbial Risk Assessment for Waterborne Viruses, Bacteria, and Protozoa in Public Water Supply Wells in Minnesota. Environ. Sci. Technol. 2021, 56, 6315–6324. [Google Scholar] [CrossRef]
- Olalemi, A.O.; Ige, O.M.; James, G.A.; Obasoro, F.I.; Okoko, F.O.; Ogunleye, C.O. Detection of enteric bacteria in t w o groundwater sources a n d associated microbial health risks. J. Water Health 2021, 19, 322–335. [Google Scholar] [CrossRef]
- Chuah, J.C.; Ziegler, A.D. Temporal Variability of Faecal Contamination from On-Site Sanitation Systems in the Groundwater of Northern Thailand. Environ. Manag. 2018, 61, 939–953. [Google Scholar] [CrossRef] [PubMed]
- Egbueri, J.C.; Ezugwu, C.K.; Ameh, P.D.; Unigwe, C.O.; Ayejoto, D.A. Appraising drinking water quality in Ikem rural area (Nigeria) based on chemometrics and multiple indexical methods. Environ. Monit. Assess. 2020, 192, 308. [Google Scholar] [CrossRef] [PubMed]
- Lima, F.S.; Scalize, P.S.; Gabriel, E.F.M.; Gomes, R.P.; Gama, A.R.; Demoliner, M.; Spilki, F.R.; Vieira, J.D.G.; Carneiro, L.C. Escherichia coli, Species C Human Adenovirus, and Enterovirus in Water Samples Consumed in Rural Areas of Goiás, Brazil. Food Environ. Virol. 2021, 14, 77–88. [Google Scholar] [CrossRef]
- Scalize, P.S.; Barros, E.F.S.; Soares, L.A.; Hora, K.E.R.; Ferreira, N.C.; Baumann, L.R.F. Avaliação da qualidade da água para abastecimento no assentamento de reforma agrária Canudos, Estado de Goiás. Rev. Ambient Água 2014, 9, 696–707. [Google Scholar] [CrossRef] [Green Version]
- Olasoji, S.O.; Oyewole, N.O.; Abiola, B.; Edokpayi, J.N. Water Quality Assessment of Surface and Groundwater Sources Using a Water Quality Index Method: A Case Study of a Peri-Urban Town in Southwest, Nigeria. Environments 2019, 6, 23. [Google Scholar] [CrossRef]
- Foster, T.; Willetts, J.; Kotra, K.K. Faecal contamination of groundwater in rural Vanuatu: Prevalence and predictors. J. Water Health 2019, 17, 737–748. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Kim, J. The Predictive Capability of a Novel Ensemble Tree-Based Algorithm for Assessing Groundwater Potential. Sustainability 2021, 13, 2459. [Google Scholar] [CrossRef]
- Jenifer, M.A.; Jha, M.K.; Khatun, A. Assessing Multi-Criteria Decision Analysis Models for Predicting Groundwater Quality in a River Basin of South India. Sustainability 2021, 13, 6719. [Google Scholar] [CrossRef]
- Jang, C.S. Aquifer vulnerability assessment for fecal coliform bacteria using multi-threshold logistic Regression. Environ. Monit. Assess. 2022, 194, 800–815. [Google Scholar] [CrossRef] [PubMed]
- Kulinkina, A.V.; Sodipo, M.O.; Schultes, O.L.; Osei, B.G.; Agyapong, E.A.; Egorov, A.I.; Naumova, E.N.; Kosinski, K.C. Rural Ghanaian households are more likely to use alternative unimproved water sources when water from boreholes has undesirable organoleptic characteristics. Int. J. Hyg. Environ. Health 2020, 227, 113514. [Google Scholar] [CrossRef] [PubMed]
- Jang, C.S. Using multi-threshold regression techniques to assess river fecal pollution in the highly urbanized Tamsui River watershed. Environ. Monit. Assess. 2021, 193, 113–126. [Google Scholar] [CrossRef]
- Otabbong, E.; Arkhipchenko, I.; Orlova, O.; Barbolina, I.; Shubaeva, M. Impact of piggery slurry lagoon on the environment: A study of groundwater and river Igolinka at the Vostochnii Pig Farm, St. Petersburg, Russia. Acta Agric. Scand. B Soil Plant Sci. 2007, 57, 74–81. [Google Scholar] [CrossRef]
- Tonetti, A.L.; Brasil, A.L.; Madrid, F.J.P.L.; Figueiredo, I.C.S.; Schneider, J.; Cruz, L.M.O.; Duarte, N.C.; Fernandes, P.M.; Coasaca, R.L.; Garcia, R.S.; et al. Tratamento de Esgotos Domésticos em Comunidades Isoladas: Referencial Para a Escolha de Soluções, 1st ed.; Biblioteca/Unicamp: Campinas, SP, Brazil, 2018; 153p. [Google Scholar]
- Chukwuma, O.M.; Ifeanyichukwu, M.K. Influence of environmental factors on the physico-chemical andbacteriological quality of well and borehole water in rural communities of udenu lga of Enugu State, Nigeria. Pak. J. Nutr. 2018, 17, 596–608. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Vining, G. Generalized Linear Models: With Applications in Engineering and the Sciences; John Willey: New York, NY, USA, 2012; 520p. [Google Scholar]
- Sperandei, S. Understanding Logistic Regression Analysis. Biochem. Med. 2013, 24, 12–18. [Google Scholar] [CrossRef]
- Box, G.E.P.; Tidwell, P.W. Transformation of the Independent Variables. Technometrics 1962, 4, 531–550. [Google Scholar] [CrossRef]
- Cunha, J.P.Z. Um Estudo Comparativo das Técnicas de Validação Cruzada Aplicadas a Modelos Mistos. Dissertação (Mestrado), Programa de Estatística; Instituto de Matemática e Estatística—Universidade de São Paulo: Butantã, SP, Brazil, 2019; Volume 1, p. 59. [Google Scholar] [CrossRef] [Green Version]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Belsley, D.A.; Kuh, E.; Welsch, R.E. Regression Diagnostics: Identifying Influential Data and Sources of Collinearity; John Wiley: New York, NY, USA, 1980; 300p. [Google Scholar]
- Nurunnabi, A.A.R.; Imon, A.H.M.R.; Nasser, M. Identification of multiple influential observations in logistic regression. J. Appl. Stat. 2010, 37, 1605–1624. [Google Scholar] [CrossRef]
- Machado, A.; Amorim, E.; Bordalo, A.A. Spatial and Seasonal Drinking Water Quality Assessment in a Sub-Saharan Country (Guinea-Bissau). Water 2022, 14, 1987. [Google Scholar] [CrossRef]
- O’dwyer, J.; Hynds, P.D.; Byrne, K.A.; Ryan, M.P.; Adley, C.C. Development of a hierarchical model for predicting microbiological contamination of private groundwater supplies in a geologically heterogeneous region. Environ. Pollut. 2018, 237, 329–338. [Google Scholar] [CrossRef]
- Munyebvu, F.; Mujere, N.; Isaac, R.K.; Eslamian, S. Assessing the microbiological quality of potable groundwater from selected protected and unprotected wells in Murehwa district, Zimbabwe. In Advances in Hydrogeochemistry Research, 1st ed.; Nova Science Publishers: New York, NY, USA, 2020; 387p. [Google Scholar]
- Kazama, S.; Takizawa, S. Evaluation of Microbial Contamination of Groundwater under Different Topographic Conditions and Household Water Treatment Systems in Special Region of Yogyakarta Province, Indonesia. Water 2021, 13, 1673. [Google Scholar] [CrossRef]
- Malla, B.; Shrestha, R.G.; Tandukar, S.; Bhandari, D.; Inoue, D.; Sei, K.; Tanaka, Y.; Sherchand, J.B.; Haramoto, E. Identificação de Contaminação Fecal Humana e Animal em Fontes de Água Potável no Vale de Kathmandu, Nepal, Usando Ensaios de PCR Quantitativos Bacteroidales Associados ao Hospedeiro. Água 2018, 10, 1796. [Google Scholar] [CrossRef] [Green Version]
- Díaz-Alcaide, S.; Martínez-Santos, P. Mapping fecal pollution in rural groundwater supplies by means of artificial intelligence classifiers. J. Hydrology 2019, 577, 124006. [Google Scholar] [CrossRef]
- Wickramasooriya, A.; Gunarathne, S.; Ekanayaka, S. Effect of Subsurface Geological Conditions on Variation of Groundwater Quality in Part of Kurunegala, Sri Lanka; Abrunhosa, M., Chambel, A., Peppoloni, S., Chaminé, H.I., Eds.; Advances in Geoethics and Groundwater Management: Theory and Practice for a Sustainable Development; Springer: Berlin/Heidelberg, Germany, 2021; pp. 233–237. [Google Scholar] [CrossRef]
- Nasir, M.J.; Tufail, M.; Ayaz, T.; Khan, S.; Khan, A.Z.; Lei, M. Groundwater quality assessment and its vulnerability to pollution: A study of district Nowshera, Khyber Pakhtunkhwa, Pakistan. Environ. Monit. Assess. 2022, 194, 692–719. [Google Scholar] [CrossRef]
- He, L.Y.; Ying, G.G.; Liu, Y.S.; Su, H.C.; Chen, J.; Liu, S.S.; Zhao, J.L. Discharge of swine wastes risks water quality and food safety: Antibiotics and antibiotic resistance genes from swine sources to the receiving environments. Environ. Int. 2016, 92–93, 210–219. [Google Scholar] [CrossRef]
- Brisola, M.C.; Crecencio, R.B.; Bitner, D.S.; Frigo, A.; Rampazzo, L.; Stefani, L.M.; Faria, G.A. Escherichia coli used as a biomarker of antimicrobial resistance in pig farms of Southern Brazil. Sci. Total Environ. 2019, 647, 362–368. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Philp, R.P.; Biache, C. Assessment of Fecal Contamination in Oklahoma Water Systems through the Use of Sterol Fingerprints. Environments 2016, 3, 28. [Google Scholar] [CrossRef] [Green Version]
- Amir, M.; Riaz, M.; Chang, Y.-F.; Ismail, A.; Hameed, A.; Ahsin, M. Antibiotic Resistance in Diarrheagenic Escherichia coli Isolated from Broiler Chickens in Pakistan. J. Food Qual. Hazards Control 2021, 8, 78–86. [Google Scholar] [CrossRef]
- van den Bogaard, A.E.; Londres, N.; Driessen, C.; Stobberingh, E.E. Antibiotic resistance of faecal Escherichia coli in poultry, poultry farmers and poultry slaughterers. J. Antimicrob. Chemother. 2021, 47, 763–771. [Google Scholar] [CrossRef]
- Bamidele, O.; Yakubu, A.; Joseph, E.B.; Amole, T.A. Antibiotic Resistance of Bacterial Isolates from Smallholder Poultry Droppings in the Guinea Savanna Zone of Nigeria. Antibiotics 2022, 11, 973. [Google Scholar] [CrossRef] [PubMed]







| DSW Water Quality | DSW Estruture | Distance between DSW and a Possible Contamination Source | DSW Geology |
|---|---|---|---|
| Apparent color (1) | Sidewalk width (1) | Distance from the corral to DSW (1) | Soil type (2) |
| Turbidity (1) | DSW diameter (1) | Corral existence (2) | Groundwater type (2) |
| pH (1) | DSW coverage (2) | Distance from pigsty to DSW (3) | |
| Total coliforms (1) | Use of exclusive pump for water collection (2) | Pigsty existence (2) | |
| Protection wall height (1) | Poultry farming (2) | ||
| Fence around DSW (2) | Distance from hennery to DSW (1) | ||
| Property flooding (2) | Hennery existence (2) | ||
| Permeable SS existence (2) | |||
| Distance from permeable SS to DSW (1) | |||
| Distance from permeable SS to DSW (3) |
| Distribution | b(θ) | θ | ϕ | |
|---|---|---|---|---|
| Normal (µ,σ2) | θ2/2 | µ | σ2 | |
| Poisson (µ) | eθ | log(µ) | 1 | −log(y!) |
| Binomial (m,) | m log(1 + eθ) | log(µ/(m − µ)) | 1 | log |
| Gama (µ,ν) | −log(−θ) | −1/µ | ν−1 | νlog(νy) − log(y) − log() |
| Inverse Normal (µ,σ2) | − | −1/2µ2 | σ2 |
| Distribution | Normal | Binomial | Poisson | Gama | N. Inverse |
|---|---|---|---|---|---|
| Canonical link | µ = η | log{µ/(1 − µ)} = η | logµ = η | µ−1 = η | µ−2 = η |
| Group of Predictor Variables | Parameter | Normal Distribution | Continuous Variable | Qualitative Variable |
|---|---|---|---|---|
| T Student | Mann-Whitney | Fisher | ||
| p-Values | p-Values | p-Values | ||
| DSW water quality | Apparent color (1) | NA | 0.070 (*) | NA |
| Turbidity (1) | NA | 0.062 (*) | NA | |
| pH (1) | 0.103 (*) | NA | NA | |
| Total coliforms (1) | NA | 0.000 (*) | NA | |
| DSW Structure | Sidewalk width (1) | NA | 0.002 (*) | NA |
| DSW depth (1) | NA | 0.467 | NA | |
| DSW diameter (1) | NA | 0.096 (*) | NA | |
| Use of exclusive pump for water collection (2) | NA | NA | 1 | |
| Protection wall height (1) | NA | 0.776 | NA | |
| DSW coverage (2) | NA | NA | 0.571 | |
| Fence around DSW (2) | NA | NA | 1 | |
| Property flooding (2) | NA | NA | 0.395 | |
| Distance between DSW and a possible contamination source | Distance from the corral to DSW (1) | NA | 0.199 (*) | NA |
| Corral existence (2) | NA | NA | 0.181 (*) | |
| Distance from pigsty to DSW (3) | NA | 0.803 | NA | |
| Pigsty existence (2) | NA | NA | 0.001 (*) | |
| Poultry farming (2) | NA | NA | 0.000 (*) | |
| Distance from hennery to DSW (1) | NA | 0.626 | NA | |
| Hennery existence (2) | NA | NA | 0.428 | |
| Distance from permeable SS to DSW (1) | NA | 0.654 | NA | |
| Permeable SS existence (2) | NA | NA | 0.034 (*) | |
| DSW Geology | Soil type (2) | NA | NA | 0.046 (*) |
| Groundwater type (2) | NA | NA | 0.045 (*) |
| Group of Predictor Variables | Code | Parameter | Selection Criteria | |
|---|---|---|---|---|
| AIC | BIC | |||
| DSW water quality | AC | Apparent color (1) | No | No |
| TURB | Turbidity (1) | Yes | Yes | |
| pH | pH (1) | No | No | |
| TC | Total coliforms (1) | No | No | |
| DSW structure | SW | Sidewalk width (1) | Yes | Yes |
| DD | DSW diameter (1) | Yes | Yes | |
| Distance between DSW and possible contamination source | Cr | Corral existence (2) | No | No |
| Pe | Pigsty existence (2) | Yes | Yes | |
| Pe class | Distance from pigsty to DSW (3) | No | No | |
| Po | Poultry farming (2) | Yes | Yes | |
| SS | Permeable SS existence (2) | No | No | |
| DSW Geology | ST | Soil type (2) | No | No |
| GWT | Groundwater type (2) | No | No | |
| Estimate (βm) | Standard Error | Z Value | Pr (>Z) | OR | |
|---|---|---|---|---|---|
| Intercept (β0) | −2.7647 | 1.3995 | −1.976 | 0.0482 * | 0.0630 |
| DD | 1.5476 | 0.8754 | 1.768 | 0.0771 ** | 4.7001 |
| SW | −1.5171 | 0.6654 | −2.280 | 0.0226 * | 0.2193 |
| Pe | 1.1677 | 0.5256 | 2.222 | 0.0263 * | 3.2147 |
| Po | 1.4799 | 0.6415 | 2.307 | 0.0211 * | 4.3925 |
| Present | Absent | ||
|---|---|---|---|
| Prediction | Present | 83 | 18 |
| Absent | 2 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, H.T.L.; Baumann, L.R.F.; Scalize, P.S. A Contamination Predictive Model for Escherichia coli in Rural Communities Dug Shallow Wells. Sustainability 2023, 15, 2408. https://doi.org/10.3390/su15032408
Lopes HTL, Baumann LRF, Scalize PS. A Contamination Predictive Model for Escherichia coli in Rural Communities Dug Shallow Wells. Sustainability. 2023; 15(3):2408. https://doi.org/10.3390/su15032408
Chicago/Turabian StyleLopes, Hítalo Tobias Lôbo, Luis Rodrigo Fernandes Baumann, and Paulo Sérgio Scalize. 2023. "A Contamination Predictive Model for Escherichia coli in Rural Communities Dug Shallow Wells" Sustainability 15, no. 3: 2408. https://doi.org/10.3390/su15032408
APA StyleLopes, H. T. L., Baumann, L. R. F., & Scalize, P. S. (2023). A Contamination Predictive Model for Escherichia coli in Rural Communities Dug Shallow Wells. Sustainability, 15(3), 2408. https://doi.org/10.3390/su15032408