Estimation of Soil Moisture Index Using Multi-Temporal Sentinel-1 Images over Poyang Lake Ungauged Zone
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Sentinel-1 Data
2.3. Ground Measurements
3. Methods
3.1. Linear Mixed Effects Model
3.2. Soil Moisture Index
3.3. Model Validation
4. Results
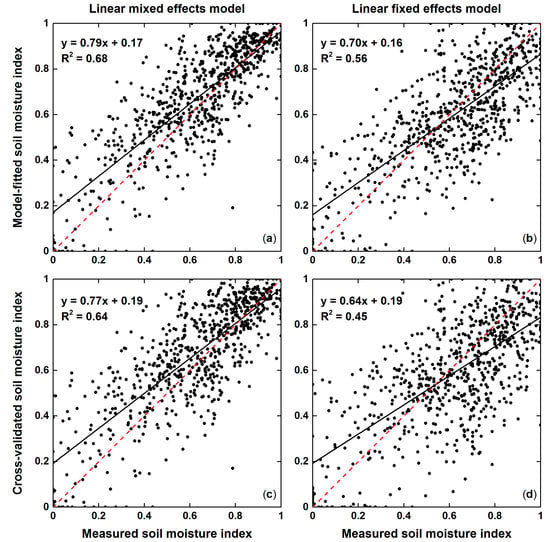
4.1. Model Fitting and Comparison
4.2. Soil Moisture Index Estimation and Validation
4.3. Soil Moisture Index Maps
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pratola, C.; Barrett, B.; Gruber, A.; Kiely, G.; Dwyer, E. Evaluation of a global soil moisture product from finer spatial resolution SAR data and ground measurements at Irish sites. Remote Sens. 2014, 6, 8190–8219. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.-C.; Bizzarri, B.; Wigneron, J.-P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Hydrol. Res. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- Scipal, K.; Drusch, M.; Wagner, W. Assimilation of a ERS scatterometer derived soil moisture index in the ECMWF numerical weather prediction system. Adv. Water Resour. 2008, 31, 1101–1112. [Google Scholar] [CrossRef]
- Saux-Picart, S.; Ottlé, C.; Decharme, B.; André, C.; Zribi, M.; Perrier, A.; Coudert, B.; Boulain, N.; Cappelaere, B.; Descroix, L. Water and energy budgets simulation over the AMMA-Niger super-site spatially constrained with remote sensing data. J. Hydrol. 2009, 375, 287–295. [Google Scholar] [CrossRef]
- Zribi, M.; Chahbi, A.; Shabou, M.; Lili-Chabaane, Z.; Duchemin, B.; Baghdadi, N.; Amri, R.; Chehbouni, A. Soil surface moisture estimation over a semi-arid region using ENVISAT ASAR radar data for soil evaporation evaluation. Hydrol. Earth Syst. Sci. 2011, 15, 345–358. [Google Scholar] [CrossRef] [Green Version]
- Brocca, L.; Melone, F.; Moramarco, T.; Wagner, W.; Naeimi, V.; Bartalis, Z.; Hasenauer, S. Improving runoff prediction through the assimilation of the ASCAT soil moisture product. Hydrol. Earth Syst. Sci. 2010, 14, 1881–1893. [Google Scholar] [CrossRef]
- Komma, J.; Blöschl, G.; Reszler, C. Soil moisture updating by Ensemble Kalman Filtering in real-time flood forecasting. J. Hydrol. 2008, 357, 228–242. [Google Scholar] [CrossRef]
- Zhang, Q.; Ye, X.-C.; Werner, A.D.; Li, Y.-L.; Yao, J.; Li, X.-H.; Xu, C.-Y. An investigation of enhanced recessions in Poyang Lake: Comparison of Yangtze River and local catchment impacts. J. Hydrol. 2014, 517, 425–434. [Google Scholar] [CrossRef]
- Ye, X.; Zhang, Q.; Liu, J.; Li, X.; Xu, C.-Y. Distinguishing the relative impacts of climate change and human activities on variation of streamflow in the Poyang Lake catchment, China. J. Hydrol. 2013, 494, 83–95. [Google Scholar] [CrossRef]
- Ye, X.; Zhang, Q.; Bai, L.; Hu, Q. A modeling study of catchment discharge to Poyang Lake under future climate in China. Quat. Int. 2011, 244, 221–229. [Google Scholar] [CrossRef]
- Chen, Y.; Xiong, W.; Wang, G. Soil and water conservation and its sustainable development of the Poyang Lake catchment in view of the 1998 flood of Yangtze River. J. Sediment Res. 2002, 4, 48–51. [Google Scholar]
- Sivapalan, M.; Takeuchi, K.; Franks, S.; Gupta, V.; Karambiri, H.; Lakshmi, V.; Liang, X.; McDonnell, J.; Mendiondo, E.; O’connell, P. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003-2012: Shaping an exciting future for the hydrological sciences. Hydrol. Sci. J. 2003, 48, 857–880. [Google Scholar] [CrossRef]
- Korres, W.; Reichenau, T.; Schneider, K. Patterns and scaling properties of surface soil moisture in an agricultural landscape: An ecohydrological modeling study. J. Hydrol. 2013, 498, 89–102. [Google Scholar] [CrossRef]
- Crow, W.T.; Berg, A.A.; Cosh, M.H.; Loew, A.; Mohanty, B.P.; Panciera, R.; Rosnay, P.; Ryu, D.; Walker, J.P. Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Cosh, M.H.; Ochsner, T.E.; McKee, L.; Dong, J.; Basara, J.B.; Evett, S.R.; Hatch, C.E.; Small, E.E.; Steele-Dunne, S.C.; Zreda, M. The soil moisture active passive marena, Oklahoma, in situ sensor testbed (smap-moisst): Testbed design and evaluation of in situ sensors. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; Oevelen, P.V. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Schmugge, T.; Gloersen, P.; Wilheit, T.; Geiger, F. Remote sensing of soil moisture with microwave radiometers. J. Geophys. Res. 1974, 79, 317–323. [Google Scholar] [CrossRef]
- Bartalis, Z.; Wagner, W.; Naeimi, V.; Hasenauer, S.; Scipal, K.; Bonekamp, H.; Figa, J.; Anderson, C. Initial soil moisture retrievals from the METOP-A advanced scatterometer (ASCAT). Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.E. The SMOS soil moisture retrieval algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A. Recent Advances in Soil Moisture Estimation from Remote Sensing. Water 2017, 9, 530. [Google Scholar] [CrossRef]
- Chen, K.; Yen, S.; Huang, W. A simple model for retrieving bare soil moisture from radar-scattering coefficients. Remote Sens. Environ. 1995, 54, 121–126. [Google Scholar] [CrossRef]
- Zribi, M.; Dechambre, M. A new empirical model to retrieve soil moisture and roughness from C-band radar data. Remote Sens. Environ. 2003, 84, 42–52. [Google Scholar] [CrossRef]
- Rahman, M.; Moran, M.; Thoma, D.; Bryant, R.; Collins, C.H.; Jackson, T.; Orr, B.; Tischler, M. Mapping surface roughness and soil moisture using multi-angle radar imagery without ancillary data. Remote Sens. Environ. 2008, 112, 391–402. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Hornacek, M.; Wagner, W.; Sabel, D.; Truong, H.-L.; Snoeij, P.; Hahmann, T.; Diedrich, E.; Doubková, M. Potential for high resolution systematic global surface soil moisture retrieval via change detection using Sentinel-1. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1303–1311. [Google Scholar] [CrossRef]
- Balenzano, A.; Mattia, F.; Satalino, G.; Pauwels, V.; Snoeij, P. SMOSAR algorithm for soil moisture retrieval using Sentinel-1 data. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 1200–1203. [Google Scholar]
- Pierdicca, N.; Pulvirenti, L.; Pace, G. A prototype software package to retrieve soil moisture from Sentinel-1 data by using a bayesian multitemporal algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 153–166. [Google Scholar] [CrossRef]
- Paloscia, S.; Pettinato, S.; Santi, E.; Notarnicola, C.; Pasolli, L.; Reppucci, A. Soil moisture mapping using Sentinel-1 images: Algorithm and preliminary validation. Remote Sens. Environ. 2013, 134, 234–248. [Google Scholar] [CrossRef]
- Lee, H.; Liu, Y.; Coull, B.; Schwartz, J.; Koutrakis, P. A novel calibration approach of MODIS AOD data to predict PM2. 5 concentrations. Atmos. Chem. Phys. 2011, 11, 9769–9795. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, Y.; Zhang, K.; Dong, W.; Lv, B.; Bai, Y. Daily estimation of ground-level PM2.5 concentrations over Beijing using 3 km resolution MODIS AOD. Environ. Sci. Technol. 2015, 49, 12280–12288. [Google Scholar] [CrossRef] [PubMed]
- Kloog, I.; Koutrakis, P.; Coull, B.A.; Lee, H.J.; Schwartz, J. Assessing temporally and spatially resolved PM2.5 exposures for epidemiological studies using satellite aerosol optical depth measurements. Atmos. Environ. 2011, 45, 6267–6275. [Google Scholar] [CrossRef]
- Kloog, I.; Nordio, F.; Coull, B.A.; Schwartz, J. Incorporating local land use regression and satellite aerosol optical depth in a hybrid model of spatiotemporal PM2.5 exposures in the Mid-Atlantic states. Environ. Sci. Technol. 2012, 46, 11913–11921. [Google Scholar] [CrossRef] [PubMed]
- Finlayson, M.; Harris, J.; McCartney, M.; Lew, Y.; Zhang, C. Report on Ramsar Visit to Poyang Lake Ramsar Site, P.R. China. Available online: http://archive.ramsar.org/pdf/Poyang_lake_report_v8.pdf (accessed on 1 November 2017).
- Zhang, L.; Lu, J.; Chen, X.; Sauvage, S.; Perez, J.-M.S. Stream flow simulation and verification in ungauged zones by coupling hydrological and hydrodynamic models: A case study of the Poyang Lake ungauged zone. Hydrol. Earth Syst. Sci. 2017, 21, 5847–5861. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Chen, X.; Cai, X.; Tian, L.; Gan, W. Assessment of inundation changes of Poyang Lake using MODIS observations between 2000 and 2010. Remote Sens. Environ. 2012, 121, 80–92. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Q.; Xu, C.-Y. Assessing the performance of satellite-based precipitation products and its dependence on topography over Poyang Lake basin. Theor. Appl. Climatol. 2014, 115, 713–729. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Chen, X.; Li, R.; Tian, L.; Murch, B. MODIS observations of the bottom topography and its inter-annual variability of Poyang Lake. Remote Sens. Environ. 2011, 115, 2729–2741. [Google Scholar] [CrossRef]
- Potin, P.; Rosich, B.; Grimont, P.; Miranda, N.; Shurmer, I.; O’Connell, A.; Torres, R.; Krassenburg, M. Sentinel-1 mission status. In Proceedings of the EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016; pp. 59–64. [Google Scholar]
- Sentinel-1 User Handbook. Available online: https://sentinel.esa.int/documents/247904/685163/Sentinel-1_User_Handbook (accessed on 1 November 2017).
- Copernicus Open Access Hub. Available online: https://scihub.copernicus.eu/ (accessed on 1 November 2017).
- Sentinel Application Platform. Available online: http://step.esa.int/main/toolboxes/snap/ (accessed on 1 November 2017).
- Lee, J.-S.; Wen, J.-H.; Ainsworth, T.L.; Chen, K.-S.; Chen, A.J. Improved sigma filter for speckle filtering of SAR imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 202–213. [Google Scholar]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. Available online: http://www.cgiar-csi.org/data/srtm-90m-digital-elevation-database-v4-1 (accessed on 1 November 2017).
- Shanghai Chang Wang Meteotech Co., Ltd. Available online: http://www.cwqx.com/ (accessed on 1 November 2017).
- Robock, A.; Vinnikov, K.Y.; Srinivasan, G.; Entin, J.K.; Hollinger, S.E.; Speranskaya, N.A.; Liu, S.; Namkhai, A. The global soil moisture data bank. Bull. Am. Meterol. Soc. 2000, 81, 1281–1299. [Google Scholar] [CrossRef]
- China Meteorological Data Sharing Service System. Available online: http://data.cma.cn/ (accessed on 1 November 2017).
- Dobson, M.C.; Ulaby, F.T. Active microwave soil moisture research. IEEE Trans. Geosci. Remote Sens. 1986, 24, 23–36. [Google Scholar] [CrossRef]
- Wagner, W.; Noll, J.; Borgeaud, M.; Rott, H. Monitoring soil moisture over the Canadian Prairies with the ERS scatterometer. IEEE Trans. Geosci. Remote Sens. 1999, 37, 206–216. [Google Scholar] [CrossRef]
- Fitzmaurice, G.M.; Laird, N.M.; Ware, J.H. Applied Longitudinal Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2004; pp. 187–188. [Google Scholar]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67. [Google Scholar] [CrossRef]
- McNairn, H.; Brisco, B. The application of C-band polarimetric SAR for agriculture: A review. Can. J. Remote Sens. 2004, 30, 525–542. [Google Scholar] [CrossRef]
- Albergel, C.; Rüdiger, C.; Carrer, D.; Calvet, J.-C.; Fritz, N.; Naeimi, V.; Bartalis, Z.; Hasenauer, S. An evaluation of ASCAT surface soil moisture products with in-situ observations in Southwestern France. Hydrol. Earth Syst. Sci. 2009, 13, 115–124. [Google Scholar] [CrossRef]
- Vereecken, H.; Kamai, T.; Harter, T.; Kasteel, R.; Hopmans, J.; Vanderborght, J. Explaining soil moisture variability as a function of mean soil moisture: A stochastic unsaturated flow perspective. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Brocca, L.; Morbidelli, R.; Melone, F.; Moramarco, T. Soil moisture spatial variability in experimental areas of central Italy. J. Hydrol. 2007, 333, 356–373. [Google Scholar] [CrossRef]
- Pierdicca, N.; Pulvirenti, L.; Bignami, C. Soil moisture estimation over vegetated terrains using multitemporal remote sensing data. Remote Sens. Environ. 2010, 114, 440–448. [Google Scholar] [CrossRef]
- Pathe, C.; Wagner, W.; Sabel, D.; Doubkova, M.; Basara, J.B. Using ENVISAT ASAR global mode data for surface soil moisture retrieval over Oklahoma, USA. IEEE Trans. Geosci. Remote Sens. 2009, 47, 468–480. [Google Scholar] [CrossRef]
- Brocca, L.; Zucco, G.; Mittelbach, H.; Moramarco, T.; Seneviratne, S.I. Absolute versus temporal anomaly and percent of saturation soil moisture spatial variability for six networks worldwide. Water Resour. Res. 2015, 50, 5560–5576. [Google Scholar] [CrossRef]
- Schmugge, T.J. Remote sensing of soil moisture: Recent advances. IEEE Trans. Geosci. Remote Sens. 1983, GE-21, 336–344. [Google Scholar] [CrossRef]







| Year | Month | Day | ∆days | Sensor |
|---|---|---|---|---|
| 2015 | April | 18 | / | A |
| May | 24 | 36 | ||
| June | 05, 29 | 12, 24 | ||
| July | 11, 23 | 12, 12 | ||
| August | 16 | 24 | ||
| September | 09, 21 | 24, 12 | ||
| October | 03, 15, 27 | 12, 12, 12 | ||
| November | 20 | 24 | ||
| December | 02, 14, 26 | 12, 12, 12 | ||
| 2016 | January | 07, 19, 31 | 12, 12, 12 | A |
| February | 24 | 24 | ||
| March | 07, 19, 31 | 12, 12, 12 | ||
| April | 12, 24 | 12, 12 | ||
| May | 06, 18, 30 | 12, 12, 12 | ||
| June | 11 | 12 | ||
| July | 05, 17 | 24, 12 | ||
| August | 10, 22 | 24, 12 | ||
| September | 15, 27 | 24, 12 | ||
| October | 03, 09, 15, 21, 27 | 6, 6, 6, 6, 6 | B, A, B, A, B | |
| November | 02, 08, 14, 26 | 6, 6, 6, 12 | A, B, A, A | |
| December | 02, 08, 14, 20, 26 | 6, 6, 6, 6, 6 | B, A, B, A, B |
| ID | Site Name | Height (m) | Land Cover | Mean (%) | Min (%) | Max (%) | Std. (%) |
|---|---|---|---|---|---|---|---|
| 1 | Dongxiang | 36.6 | Nursery | 33.08 | 23.20 | 39.10 | 3.93 |
| 2 | Yongxiu | 14 | Paddy field | 47.30 | 32.90 | 56.90 | 7.17 |
| 3 | Duchang | 37.7 | Dryland | 20.83 | 4.50 | 31.00 | 5.90 |
| 4 | Xingzi | 62 | Dryland | 30.63 | 16.50 | 39.90 | 4.93 |
| 5 | Fengcheng | 26 | Paddy field | 39.70 | 30.90 | 45.50 | 3.87 |
| 6 | Wannian | 51.7 | Grassland | 30.03 | 19.30 | 40.80 | 4.20 |
| 7 | Fengxin | 75 | Orchard | 30.66 | 24.00 | 34.90 | 2.50 |
| 8 | Hukou | 39.6 | Grassland | 26.81 | 11.30 | 35.80 | 5.95 |
| 9 | Nanchang | 29.9 | Dryland | 27.35 | 20.80 | 30.80 | 2.96 |
| 10 | Ruichang | 23.6 | Dryland | 35.15 | 26.40 | 38.70 | 3.04 |
| 11 | Leping | 26 | Dryland | 30.16 | 22.20 | 35.70 | 3.15 |
| 12 | Yugan | 19 | Dryland | 26.94 | 12.00 | 33.90 | 5.20 |
| 13 | Zhangshu | 29 | Dryland | 32.80 | 27.50 | 36.70 | 2.40 |
| 14 | Gaoan | 34 | Dryland | 27.17 | 19.90 | 30.30 | 2.54 |
| 15 | Xinjian | 7 | Dryland | 20.75 | 13.30 | 24.90 | 2.19 |
| Model | Fixed Slop | Fixed Intercept | Overall R2 | RMSE (%) | MPE (%) |
|---|---|---|---|---|---|
| VV | 0.33 * | 33.36 * | 0.894 | 2.53 | 1.87 |
| VH | 0.13 | 32.54 * | 0.892 | 2.56 | 1.90 |
| VV + VH | VV: 0.34 *; VH: −0.03 | 32.98 * | 0.860 | 3.12 | 2.45 |
| Model | Temporal R2 | Spatial R2 | Overall R2 | RMSE (%) | MPE (%) |
|---|---|---|---|---|---|
| Fixed | 0.558 | 0.671 | 0.219 | 6.88 | 5.14 |
| Mixed (full) | 0.641 | 1 | 0.894 | 2.53 | 1.87 |
| Mixed (without ) | 0.613 | 0.052 | 0.171 | 7.16 | 5.23 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Gong, J.; Sun, K.; Yin, J.; Chen, X. Estimation of Soil Moisture Index Using Multi-Temporal Sentinel-1 Images over Poyang Lake Ungauged Zone. Remote Sens. 2018, 10, 12. https://doi.org/10.3390/rs10010012
Zhang Y, Gong J, Sun K, Yin J, Chen X. Estimation of Soil Moisture Index Using Multi-Temporal Sentinel-1 Images over Poyang Lake Ungauged Zone. Remote Sensing. 2018; 10(1):12. https://doi.org/10.3390/rs10010012
Chicago/Turabian StyleZhang, Yufang, Jianya Gong, Kun Sun, Jianmin Yin, and Xiaoling Chen. 2018. "Estimation of Soil Moisture Index Using Multi-Temporal Sentinel-1 Images over Poyang Lake Ungauged Zone" Remote Sensing 10, no. 1: 12. https://doi.org/10.3390/rs10010012
APA StyleZhang, Y., Gong, J., Sun, K., Yin, J., & Chen, X. (2018). Estimation of Soil Moisture Index Using Multi-Temporal Sentinel-1 Images over Poyang Lake Ungauged Zone. Remote Sensing, 10(1), 12. https://doi.org/10.3390/rs10010012