Assessing the Performance of a Low-Cost Method for Video-Monitoring the Water Surface and Bed Level in the Swash Zone of Natural Beaches
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Set Up
2.2. Field Data
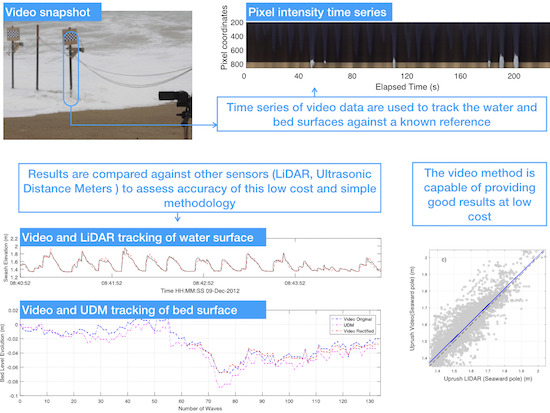
2.3. Image Processing
2.4. Bed Level and Water Surface Detection
3. Results
3.1. Comparison with LiDAR for the Water Surface and Bed Level
3.2. Comparison with Ultrasonic Distance Meters (UDM) for the Bed Level
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Elfrink, B.; Baldock, T. Hydrodynamics and sediment transport in the swash zone: A review and perspectives. Coast. Eng. 2002, 45, 149–167. [Google Scholar] [CrossRef]
- Masselink, G.; Puleo, J.A. Swash-zone morphodynamics. Cont. Shelf Res. 2006, 26, 661–680. [Google Scholar] [CrossRef]
- Brocchini, M.; Baldock, T.E. Recent advances in modeling swash zone dynamics: Influence of surf-swash interaction on nearshore hydrodynamics and morphodynamics. Rev. Geophys. 2008, 46. [Google Scholar] [CrossRef]
- Puleo, J.A.; Butt, T. The first international workshop on swash-zone processes. Cont. Shelf Res. 2006, 26, 556–560. [Google Scholar] [CrossRef]
- Hughes, M.G.; Masselink, G.; Brander, R.W. Flow velocity and sediment transport in the swash zone of a steep beach. Mar. Geol. 1997, 138, 91–103. [Google Scholar] [CrossRef]
- Blenkinsopp, C.; Turner, I.; Masselink, G.; Russell, P. Swash zone sediment fluxes: Field observations. Coast. Eng. 2011, 58, 28–44. [Google Scholar] [CrossRef]
- Puleo, J.; Lanckriet, T.; Blenkinsopp, C. Bed level fluctuations in the inner surf and swash zone of a dissipative beach. Mar. Geol. 2014, 349, 99–112. [Google Scholar] [CrossRef]
- Blenkinsopp, C.; Mole, M.; Turner, I.; Peirson, W. Measurements of the time-varying free-surface profile across the swash zone obtained using an industrial LIDAR. Coast. Eng. 2010, 57, 1059–1065. [Google Scholar] [CrossRef]
- Holman, R.; Guza, R. Measuring run-up on a natural beach. Coast. Eng. 1984, 8, 129–140. [Google Scholar] [CrossRef]
- Holland, K.T.; Raubenheimer, B.; Guza, R.T.; Holman, R.A. Runup kinematics on a natural beach. J. Geophys. Res. Oceans 1995, 100, 4985–4993. [Google Scholar] [CrossRef]
- Raubenheimer, B.; Guza, R.T.; Elgar, S.; Kobayashi, N. Swash on a gently sloping beach. J. Geophys. Res. Oceans 1995, 100, 8751–8760. [Google Scholar] [CrossRef]
- Masselink, G.; Russell, P. Flow velocities, sediment transport and morphological change in the swash zone of two contrasting beaches. Mar. Geol. 2006, 227, 227–240. [Google Scholar] [CrossRef]
- Cox, D.T.; Shin, S. Laboratory Measurements of Void Fraction and Turbulence in the Bore Region of Surf Zone Waves. J. Eng. Mech. 2003, 129, 1197–1205. [Google Scholar] [CrossRef]
- Lanckriet, T.; Puleo, J.A.; Masselink, G.; Turner, I.; Conley, D.; Blenkinsopp, C.; Russell, P. Comprehensive Field Study of Swash-Zone Processes. II: Sheet Flow Sediment Concentrations during Quasi-Steady Backwash. J. Waterway Port Coast. Ocean Eng. 2014, 140, 29–42. [Google Scholar] [CrossRef] [Green Version]
- Turner, I.L.; Russell, P.E.; Butt, T. Measurement of wave-by-wave bed-levels in the swash zone. Coast. Eng. 2008, 55, 1237–1242. [Google Scholar] [CrossRef]
- Masselink, G.; Russell, P.; Turner, I.; Blenkinsopp, C. Net sediment transport and morphological change in the swash zone of a high-energy sandy beach from swash event to tidal cycle time scales. Mar. Geol. 2009, 267, 18–35. [Google Scholar] [CrossRef]
- Baldock, T. Discussion of “Measurement of wave-by-wave bed-levels in the swash zone” by Ian L. Turner, Paul E. Russell, Tony Butt [Coastal Eng. 55 (2008) 1237–1242]. Coast. Eng. 2009, 56, 380–381. [Google Scholar] [CrossRef]
- Vousdoukas, M.; Kirupakaramoorthy, T.; Oumeraci, H.; de la Torre, M.; Wübbold, F.; Wagner, B.; Schimmels, S. The role of combined laser scanning and video techniques in monitoring wave-by-wave swash zone processes. Coast. Eng. 2014, 83, 150–165. [Google Scholar] [CrossRef]
- Almeida, L.; Masselink, G.; Russell, P.; Davidson, M. Observations of gravel beach dynamics during high energy wave conditions using a laser scanner. Geomorphology 2015, 228, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Martins, K.; Blenkinsopp, C.E.; Zang, J. Monitoring Individual Wave Characteristics in the Inner Surf with a 2-Dimensional Laser Scanner (LiDAR). J. Sens. 2016, 83, 150–165. [Google Scholar] [CrossRef]
- Brodie, K.L.; Raubenheimer, B.; Elgar, S.; Slocum, R.K.; McNinch, J.E. Lidar and Pressure Measurements of Inner-Surfzone Waves and Setup. J. Atmos. Ocean. Technol. 2015, 32, 1945–1959. [Google Scholar] [CrossRef]
- Hofland, B.; Diamantidou, E.; van Steeg, P.; Meys, P. Wave runup and wave overtopping measurements using a laser scanner. Coast. Eng. 2015, 106, 20–29. [Google Scholar] [CrossRef]
- Aagaard, T.; Holm, J. Digitization of Wave Run-up Using Video Records. J. Coast. Res. 1989, 5, 547–551. [Google Scholar]
- Power, H.E.; Holman, R.A.; Baldock, T.E. Swash zone boundary conditions derived from optical remote sensing of swash zone flow patterns. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Almar, R.; Blenkinsopp, C.; Almeida, L.P.; Cienfuegos, R.; Catalán, P.A. Wave runup video motion detection using the Radon Transform. Coast. Eng. 2017, 130, 46–51. [Google Scholar] [CrossRef]
- Holland, K.T.; Puleo, J.A. Variable swash motions associated with foreshore profile change. J. Geophys. Res. Oceans 2001, 106, 4613–4623. [Google Scholar] [CrossRef]
- Holland, K.T.; Holman, R.A. Video Estimation of Foreshore Topography Using Trinocular Stereo. J. Coast. Res. 1997, 13, 81–87. [Google Scholar]
- Astier, J.; Astruc, D.; Lacaze, L.; Eiff, O. Investigation of the Swash Zone Evolution At Wave Time Scale. Coast. Eng. Proc. 2012, 1, 48. [Google Scholar] [CrossRef]
- Astruc, D.; Cazin, S.; Cid, E.; Eiff, O.; Lacaze, L.; Robin, P.; Toublanc, F.; Cáceres, I. A stereoscopic method for rapid monitoring of the spatio-temporal evolution of the sand-bed elevation in the swash zone. Coast. Eng. 2012, 60, 11–20. [Google Scholar] [CrossRef]
- Chardón-Maldonado, P.; Pintado-Patino, J.C.; Puleo, J.A. Advances in swash-zone research: Small-scale hydrodynamic and sediment transport processes. Coast. Eng. 2016, 115, 8–25. [Google Scholar] [CrossRef]
- Mizuguchi, M. Swash on a Natural Beach. In Proceedings of the International Conference on Coastal Engineering, Houston, TX, USA, 3–7 September 1984; Volume 1. [Google Scholar]
- Ebersole, B.; Hughes, S. DUCK85 Photopole Experiment; Technical Report CERC-87-18; U.S. Army Waterways Experiment Station, Coastal Engineering Research Center: Vicksburg, MS, USA, 1987. [Google Scholar]
- Ebersole, B.; Hughes, S. SUPERDUCK Photopole Experiment; Draft Technical Report; U.S. Army Waterways Experiment Station, Coastal Engineering Research Center: Vicksburg, MS, USA, 1988. [Google Scholar]
- Weir, F.M.; Hughes, M.G.; Baldock, T.E. Beach face and berm morphodynamics fronting a coastal lagoon. Geomorphology 2006, 82, 331–346. [Google Scholar] [CrossRef]
- Larson, M.; Kubota, S.; Erikson, L. Swash-zone sediment transport and foreshore evolution: Field experiments and mathematical modeling. Mar. Geol. 2004, 212, 61–79. [Google Scholar] [CrossRef]
- Sallenger, A.H.; Richmond, B.M. High-frequency sediment-level oscillations in the swash zone. Mar. Geol. 1984, 60, 155–164. [Google Scholar] [CrossRef]
- Austin, M.J.; Masselink, G. Observations of morphological change and sediment transport on a steep gravel beach. Mar. Geol. 2006, 229, 59–77. [Google Scholar] [CrossRef]
- Austin, M.J.; Buscombe, D. Morphological change and sediment dynamics of the beach step on a macrotidal gravel beach. Mar. Geol. 2008, 249, 167–183. [Google Scholar] [CrossRef]
- Kulkarni, C.D.; Levoy, F.; Monfort, O.; Miles, J. Morphological variations of a mixed sediment beachface (Teignmouth, UK). Cont. Shelf Res. 2004, 24, 1203–1218. [Google Scholar] [CrossRef]
- Cienfuegos, R.; Villagran, M.; Aguilera, J.C.; Catalán, P.; Castelle, B.; Almar, R. Video monitoring and field measurements of a rapidly evolving coastal system: The river mouth and sand spit of the Mataquito River in Chile. J. Coast. Res. 2014, 26, 639–644. [Google Scholar] [CrossRef]
- Beyá, J.; Álvarez, M.; Gallardo, A.; Hidalgo, H.; Winckler, P. Generation and validation of the Chilean Wave Atlas database. Ocean Model. 2017, 116, 16–32. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Valentini, N.; Saponieri, A.; Damiani, L. A new video monitoring system in support of Coastal Zone Management at Apulia Region, Italy. Ocean Coast. Manag. 2017, 142, 122–135. [Google Scholar] [CrossRef]














| Pole Location | Resolution | Pole Location | Resolution (m/pixel) |
|---|---|---|---|
| (Mataquito) | (m/pixel) | (Reñaca) | (Reñaca) |
| Landward | 0.0026 | Landward | 0.0015 |
| Seaward | 0.0032 | Seaward | 0.0019 |
| Mataquito | Reñaca | |||||||
|---|---|---|---|---|---|---|---|---|
| Pole-Data | RMSE (m) | a | b | RMSE (m) | a | b | ||
| Landward Overall | 0.023 | - | - | - | - | - | - | - |
| Landward Uprush | 0.050 | 0.71 | −0.237 | 1.414 | - | - | - | - |
| Landward Backwash | 0.028 | 0.85 | 0.028 | 0.994 | - | - | - | - |
| Landward Bed level | 0.004 | 0.82 | 0.318 | 0.816 | 0.004 | 0.89 | 0.127 | 0.940 |
| Seaward Overall | 0.044 | - | - | - | - | - | - | - |
| Seaward Uprush | 0.062 | 0.81 | 0.037 | 0.986 | - | - | - | - |
| Seaward Backwash | 0.037 | 0.89 | 0.212 | 0.863 | - | - | - | - |
| Seaward Bed level | 0.005 | 0.69 | 0.091 | 0.933 | 0.009 | 0.93 | 0.243 | 0.87 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibaceta, R.; Almar, R.; Catalán, P.A.; Blenkinsopp, C.E.; Almeida, L.P.; Cienfuegos, R. Assessing the Performance of a Low-Cost Method for Video-Monitoring the Water Surface and Bed Level in the Swash Zone of Natural Beaches. Remote Sens. 2018, 10, 49. https://doi.org/10.3390/rs10010049
Ibaceta R, Almar R, Catalán PA, Blenkinsopp CE, Almeida LP, Cienfuegos R. Assessing the Performance of a Low-Cost Method for Video-Monitoring the Water Surface and Bed Level in the Swash Zone of Natural Beaches. Remote Sensing. 2018; 10(1):49. https://doi.org/10.3390/rs10010049
Chicago/Turabian StyleIbaceta, Raimundo, Rafael Almar, Patricio A. Catalán, Chris E. Blenkinsopp, Luis P. Almeida, and Rodrigo Cienfuegos. 2018. "Assessing the Performance of a Low-Cost Method for Video-Monitoring the Water Surface and Bed Level in the Swash Zone of Natural Beaches" Remote Sensing 10, no. 1: 49. https://doi.org/10.3390/rs10010049
APA StyleIbaceta, R., Almar, R., Catalán, P. A., Blenkinsopp, C. E., Almeida, L. P., & Cienfuegos, R. (2018). Assessing the Performance of a Low-Cost Method for Video-Monitoring the Water Surface and Bed Level in the Swash Zone of Natural Beaches. Remote Sensing, 10(1), 49. https://doi.org/10.3390/rs10010049