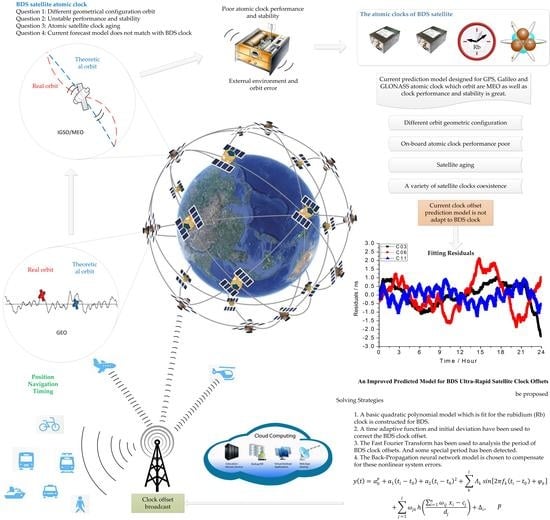
An Improved Predicted Model for BDS Ultra-Rapid Satellite Clock Offsets

Abstract

The satellite clocks used in the BeiDou-2 satellite navigation System (BDS) are Chinese self-developed Rb atomic clocks, and their performances and stabilities are worse than GPS and Galileo satellite clocks. Due to special periodic noises and nonlinear system errors existing in the BDS clock offset series, the GPS ultra-rapid clock model, which uses a simple quadratic polynomial plus one periodic is not suitable for BDS. Therefore, an improved prediction model for BDS satellite clocks is proposed in order to enhance the precision of ultra-rapid predicted clock offsets. First, a basic quadratic polynomial model which is fit for the rubidium (Rb) clock is constructed for BDS. Second, the main cyclic terms are detected and identified by the Fast Fourier Transform (FFT) method according to every satellite clock offset series. The detected results show that most BDS clocks have special cyclic terms which are different from the orbit periods. Therefore, two main cyclic terms are added to absorb the periodic effects. Third, after the quadratic polynomial plus two periodic fitting, some evident nonlinear system errors also exist in the model residual, and the Back Propagation (BP) neural network model is chosen to compensate for these nonlinear system errors. The simulation results show that the performance and precision using the improved model are better than that of China iGMAS ultra-rapid prediction (ISU-P) products and the Deutsches GeoForschungsZentrum GFZ BDS ultra-rapid prediction (GBU-P) products. Comparing to ISU-P products, the average improvements using the proposed model in 3 h, 6 h, 12 h and 24 h are 23.1%, 21.3%, 20.2%, and 19.8%, respectively. Meanwhile the accuracy improvements of the proposed model are 9.9%, 13.9%, 17.3%, and 21.2% compared to GBU-P products. In addition, the kinematic Precise Point Positioning (PPP) example using 8 Multi-GNSS Experiment MGEX stations shows that the precision based on the proposed clock model has improved about 16%, 14%, and 38% in the North (N), East (E) and Height (H) components.

1. Introduction

The precision of real-time satellite clock products has a direct impact on the capability of the Global Navigation Satellite System (GNSS) Position, Navigation, and Timing (PNT) service [1,2,3,4,5,6,7]. In the case of multi-GNSS PNT, the performances of Chinese BDS satellite clocks are no match for that of GPS and Galileo. However, the accuracy and stability of BDS clock products should be paid more attention [8,9,10,11]. The current BDS real-time clock products include three categories. The first is the real-time broadcast ephemeris, which broadcasts a set of satellite clock coefficients per hour, the user receives the coefficients, and can obtain real-time clock offsets after the quadratic polynomial fitting and forecasting. The precision of BDS broadcast ephemeris clock products is lower than six nanoseconds (ns). The second category are the Beidou ultra-rapid clock offset products, which are based on 24-h clock offset observations for real-time forecasting of 24-h clock offsets. It is updated every six hours. The accuracy of the ultra-rapid products is better than that of the broadcast ephemeris, which is ca. 2~6 ns [12,13,14,15,16]. However, the ultra-rapid clock offset product still cannot meet the requirements of the real-time navigation and positioning with decimeter precision. The last category is the real-time corrections product of the satellite clock offset, which uses real-time observation flows of local or wide-area BDS stations to estimate the satellite’s clock offset in real-time, the interval of the estimated clock offset is generally 5–10 s, and the broadcast cycle is under five minutes. The precision of the estimated clock offset is better than 0.5 ns [17,18,19,20]. However, the real-time clock product relies on high-performance processing equipment and additional stations, and it is also unstable and cannot be obtained by the common user. Generally, as one of the core products of International GNSS Service (IGS), the ultra-rapid clock offset product is an important product in decimeter-level positioning services. At present, there are only two institutes, the German GBM and Chinese ISC, which provide open BDS ultra-rapid clock products. Due to the BDS constellation consisting of Geosynchronous Orbit (GEO), Inclined Geosynchronous Satellite Orbit (IGSO), and Medium Earth Orbit (MEO) satellites, compared with the MEO satellite clocks, the GEO and IGSO satellite clocks have different periodic noises, and all BDS satellite clocks contain evident nonlinear system errors (these errors are discussed in Section 3 and Section 4). The ultra-rapid models of GPS, GLONASS, and Galileo, which include stable MEO satellite clocks, are not suitable for BDS [11,21,22]. The BDS models of GBM and ISC are similar to that of GPS by a quadratic polynomial plus one period for each satellite [22,23,24,25]. It is necessary to improve and build a more accurate BDS ultra-rapid clock prediction model.

In the previous research of real-time clock prediction, GPS clock offset predictions in the IGS ultra-rapid products were modeled by a quadratic polynomial plus one period [14]. However, the forecast result is not significantly improved compared with the broadcast ephemeris accuracy [15]. Huang used the improved model to predict the IGS ultra-rapid clock offset of GPS, but the model does not consider the nonlinear colored noise [9,26]. Wang et al. proposed a wavelet neural network model based on the single difference sequence to predict GPS clock offsets, but this model does not consider the periodic errors and the frequency shift errors [27]. In order to improve the precision of real-time clock offset prediction, the satellite clock noise type, period characteristics, frequency stability, and the physical model have been researched [9,10,13,15]. However, the previous research was mainly concentrated on the stable GPS clocks rather than the BDS clocks. In the BDS clock offset series, there exist some classified periodic errors and some evident nonlinear colored noise. Since the geometric construction, as well as the special periodic noise of the BDS satellite clocks, were different [8,15,21], the BDS clock offset prediction model must be classified according to every satellite clock.

An improved model for the BDS satellite clocks prediction is proposed to enhance the precision of BDS ultra-rapid clock products. A few personal periodic terms of every satellite clock are detected and added to absorb the periodic effects and then nonlinear residual noise is modeled by the BP neural network method to improve the prediction accuracies. Based on ISU and GBU clock offset observations, the numerical examples are designed to demonstrate the accuracy and effectiveness of the improved model.

2. BDS Satellite Orbits and Clock Status

The satellite clocks in orbit with different orbital heights have different periodic characteristics. The performance and service life of the satellite clocks in different periods are also not similar. The atomic clock types of the BDS satellites in orbit are summarized in

Table 1. The types and ages of BDS on-board satellite clocks (the list of events as of March 2017).

Generation	Lunch Date	Orbit	Status	PRN	Equipment Clock 1	Serve Time (Month)
BDS-1	2000.10.31	GEO	Not usable	S-1	Rb	None
	2000.12.21	GEO	Not usable	S-2	Rb	None
	2003.05.25	GEO	Not usable	S-3	Rb	None
	2007.02.03	GEO	Not usable	S-4	Rb	None
BDS-2	2007.04.14	MEO	Not usable	None	Rb	None
	2009.04.15	GEO	Not usable	C02	Rb	69
	2010.01.17	GEO	normal	C01	Rb	86
	2010.06.02	GEO	normal	C03	Rb	81
	2010.08.01	IGSO	normal	C06	Rb	79
	2010.11.01	GEO	normal	C04	Rb	76
	2010.12.18	IGSO	normal	C07	Rb	75
	2011.04.10	IGSO	normal	C08	Rb	71
	2011.07.27	IGSO	normal	C09	Rb	68
	2011.12.02	IGSO	normal	C10	Rb	64
	2012.02.25	GEO	normal	C05	Rb	62
	2012.04.30	MEO	normal	C11, C12	Rb	59
	2012.09.19	MEO	normal	C13, C14	Rb	53
	2012.10.25	GEO	normal	C02	Rb	52
	2015.03.30	IGSO	normal	C15 switched to C13	Rb	23
	2016.06.12	GEO	Not usable	G7	Rb	8
BDS-3 Test	2015.07.25	MEO	normal	C33, C34	Rb	19
	2015.09.30	IGSO	normal	C32	H	17
	2016.02.01	MEO	normal	C35	Rb	12
	2016.03.30	IGSO	normal	C31	Rb	11

¹ http://www.csno-tarc.cn/.

. The satellite orbit constellation geometry is shown in Figure 1.

From Table 1 it can be seen that there are in total, 20 BDS on-board satellites, of which 15 are BDS-2 satellites, and five are new BDS-3 test satellites. All the BDS satellites are currently equipped with Rb atomic clocks except for satellite C32 (which uses a Hydrogen (H) atomic clock). The longest-serving satellite is C01, which has been working for more than seven years.

It can be seen from Figure 1 that the service areas of the BDS-2 satellites focus on the Asia-Pacific region; five GEO satellites are running in a latitude and longitude within the grid perturbation, while six IGSO satellites are running around the “8”-shaped trajectory in the Asia-Pacific region. This can guarantee the number of visible satellites in the Asia-Pacific region, while three MEO satellites are running globally. The geometric configurations of three types of satellites also create the diversity of the clock periodic characteristics. The satellite and clock types in Table 1 and Figure 1 are beneficial to the classification of the satellite clock prediction models below.

This paper mainly discusses the effect of satellite clock modeling on prediction precision. In the process of clock offset estimation, the satellite orbits and clock parameters are typically estimated simultaneously. Therefore, the satellite orbit solutions have some effects on the satellite clock estimations. Due to the precise orbit determination and time synchronization method, the orbital period and type have a direct impact on the characteristics and performance of satellite clocks. In this paper, the impact of the BDS satellite clock on its heterogeneous constellation’s orbit is analyzed in Section 4.

3. Basic Predicted Model

3.1. Preprocessing of Satellite Clock Offsets

In the case of satellite clock prediction, the precision of clock offset observations directly determines the accuracy of the prediction model. Therefore, the abnormal values and blunders in the observations should be eliminated before the model has been established [27,28,29,30,31,32,33]. In this paper, the median absolute deviation (MAD) method was used to detect the phase and frequency jumps which exist in the clock offset sequence. The MAD method can be expressed as [16,24]:

$$M=\mathrm{Median}\left\{\left|b_u-m\right|/0.6745\right\},$$

(1)

where $M$ is the difference value which is the threshold value in this model. $u$ is the frequency epoch number. $m$ is the median of the clock frequency sequences, and $m=\mathrm{Median}\left\{b_u\right\}$. $b_u$ is the clock frequency sequence. It is considered as a blunder if $\left|b_u\right|>\left(m+n·M\right)$ (in this paper n was set as 3) [33,34,35]. In order to verify the MAD method, the C04 clock offsets results of 4 January 2017 were chosen as shown in Figure 2.

As shown in Figure 2a, there are more blunders existing in the data. It is not smooth in the clock frequency sequences. However, in Figure 2b, the clock offset sequence is smooth and has no significant fluctuation by using the MAD method. This method is not sensitive to the magnitude of the blunders. Usually the blunders detected just applied to the clock frequency data, and for raw clock phase data it should be converted to the original frequency data through the single difference method.

3.2. Quadratic Polynomial Model

After preprocessing, the clean clock offset sequences can be modeled. An adaptive predicting model of the BDS ultra-rapid clock offsets will be constructed, which takes into account the physical characteristics of the satellite clock, the adaptive weight function, and the initial deviation.

At present, BDS satellites are mainly equipped with Rb atomic clocks. A Rb clock has significant clock drift characteristics, therefore, the quadratic polynomial model was used as the basic prediction model and the fitting formula can be expressed as follows [34,35]:

$$y\left(t\right)=a_0+a_1\left(t_i-t_0\right)+a_2{\left(t_i-t_0\right)}^2+{∆}_i,$$

(2)

where $a_0$, $a_1$, and $a_2$ are three parameters of the satellite clock model, and they also can be called clock offset (phase), clock velocity (frequency), and clock drift (frequency drift), respectively. $t_0$ is the reference epoch of the satellite clock model, $t_i$ denotes the observation epoch, and $y\left(t\right)$ is the clock offset phase observation. ${∆}_i$ is the residual of prediction model.

In order to compare the residuals of different fitting models step by step, the fitting residuals of the BDS clock offset observations on 1 January 2017 are obtained by the quadratic polynomial, as shown in Figure 3.

As shown in Figure 3, the significant periodic characteristics exist between different constellations’ residuals after quadratic polynomial fitting. In order to ensure the correctness and reliability of the selection of the periodic terms, the FFT method is used to analyze the quadratic polynomial fitting residuals of GBM and ISU during a period of 100 days (see Section 4).

3.3. Time Adaptive Weight Function and Initial Deviation Correction

When the satellite clock model has been identified, we can use the sequential adjustment least square method to fit the clock model parameter and use the sliding window method to estimate the fitting coefficient. Usually the observation weight matrix ($\mathrm{P}$) of the clock model is assumed to be the identity matrix, although the observations near to the start of the prediction should have higher weights. For this reason, a method of equivalent weight is used, which is constructed by a function of time adaptive factors. The performance of the BDS satellite clock is almost equal to that of the GPS Block IIR clock (refer to GPS Block IIR clock results [14]). The formula of the constructed adaptive function was determined to be as follows:

$$\overline{\mathrm{P}}=\mathrm{diag}\left(p_i\right),p_i=i∆t\mathrm{Rb},$$

(3)

$$\overline{\mathrm{P}}=\left[\begin{array}{cccc}∆t& 0& 0& 0\\ 0& 2∆t& 0& 0\\ 0& 0& \ddots & ⋮\\ 0& 0& \dots & i∆t\end{array}\right],i=(1,2,\dots ,n),$$

(4)

where $i$ is the number of the observations and n is the total number of clock offset data. Rb is the type of the rubidium atomic clock, $∆t$ indicates the sample interval, $\overline{\mathrm{P}}$ is the observed equivalent weight, and $p_i$ is the diagonal of the weight matrix as shown in Equation (4). The clock offset which is nearly the start of the prediction point have higher weights.

However, comparing with actual clock observations, the prediction results of some satellites still have large deviations, which usually occur at the beginning. These deviations are called “initial deviations” [14], which also exist in the prediction results all the time. In order to keep the continuity between the observed clocks and the predictions, initial deviations, which belong to systemic errors, should be corrected in the real-time clock prediction. In order to reduce the initial deviations, a modified method, which is similar as GPS clock prediction in [14], for the constant term $a_0$ of the clock model is used. The main steps can be referred to in [14]. In case of irregular blunders and non-linear noise in the BDS clock offset series, the numerical experiments show that the adoptive weight and initial deviation correction do not enhance the accuracies evident in the real BDS clock offset prediction. Therefore, they are just introduced as an optional algorithm which has not been compared with the other improved algorithms in the experiments of Section 4.

4. Improved Algorithms

4.1. Periodic Term Detection and Classified Compensation

The satellites in orbit are affected by the orbital period and the space environment, as well as various disturbances. Therefore, the influence of orbital period and perturbation error should be considered in the satellite clock offset prediction. Considering that the significant period of the satellite clock was usually consistent with the satellite orbital period, the periodic correction with the orbital period is added to the GPS satellite clock prediction by IGS [9,14]. For the BDS satellite clock, the significant periodic terms not only include the similar orbital period, but other periodic signals that need to be analyzed also exist. In this paper, the Fast Fourier Transform (FFT) algorithm was used to obtain the significant periodic terms of all BDS satellites clocks based on 100 days in 2016 of clock offset observations [4,8,10,36]. Two significant and special periodic terms of BDS different geometric configurations are given, as shown in Figure 4 and

Table 2. Selection of BDS satellite periodic items with different geometric configurations.

BDS Satellites	Main Periodic (h)	Amplitude (ns)	Secondary Periodic (h)	Amplitude (ns)
C01	23.9	0.19	6.00	0.12
C02	24.0	0.22	12.0	0.13
C03	18.8	0.24	15.8	0.14
C04	23.9	0.25	11.8	0.10
C05	23.9	0.30	12.0	0.15
C06	12.8	0.51	16.5	0.13
C07	23.9	0.31	12.0	0.12
C08	23.9	0.26	12.0	0.13
C09	23.9	0.25	12.0	0.13
C10	23.9	0.29	12.0	0.10
C11	12.5	0.18	1.30	0.10
C12	12.3	0.21	6.30	0.09
C13	24.0	0.28	12.0	0.08
C14	12.4	0.19	6.20	0.09

. Additionally, the amplitudes of the significant periodic terms are shown in Table 2.

It can be seen from Figure 4 and Table 2 that the different types of BDS satellites are influenced by the different orbital geometric configurations. However, some period terms are not consistent with the orbital periods (see C03, C06 and C13), which are independent of their satellite devices. Usually, in the GNSS clock offset forecasting model, only the first significant period item is selected. It can be seen from Table 2 that the amplitude of the second period is about 0.1 ns, so we omit the third period (about 0.04 ns) and only choose the first periodic terms as the correction of periodic errors. The orbital period is remarkable mainly because of the usage of the precise orbit determination and time synchronization method. Through FFT analysis it can be seen that the periods are different between BDS and other GNSS. Therefore, different geometric configurations should be added with different periods, and the optimal selection of periodic items will have a more significant influence on the prediction accuracy.

In addition, from Figure 4, it can be seen that there is a special significant period in the C11 satellite, and the FFT analysis results of the C11 satellite are shown separately in Figure 5.

From Figure 5, the C11 satellite has a significant periodic term of about 1.3 h, and it is different from the normal period of the MEO orbital geometric configuration. The amplitude of this period is about 0.1 ns. This obvious period will have a large impact on the precision of the prediction model and should be considered. This noticeable period may be caused by the hardware of the atomic clock itself.

By using the same observations in Figure 4, through adding one and two significant periodic terms to the quadratic polynomial model, respectively, the fitting residuals can be corrected, and the results are shown in Figure 6.

From Figure 6, it can be seen that the fitting residuals is more stable after adding two periodic terms, and the fitting accuracies are significantly improved without obvious periodic terms. The results also verify that the existence of the periodic term between different satellites geometric configurations. It can be seen that the fitting precision of GEO and MEO are within 1 ns, and that of IGSO is superior to 1.5 ns.

In order to analyze the relationship between the residual performances and the operation years, the on-orbit operation years of BDS satellites are given in Figure 7. It can be seen that the service years of C01, C03, C04, and C06 all over six years which close to designed life (7.5 years). Similarly, the fitting accuracies of C01, C03 and C04 are worse than that of other GEO satellites (see Figure 6), and the fitting accuracies of C06 are worse than that of other IGSO satellites (see Figure 6). Therefore, the performance of BDS satellite clocks will evidently degrade during increasing years of service.

As shown in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, the fitting accuracies with the periodic terms plus the polynomial model are reached within 1 ns, and no significant periodic terms exist in the residuals. In order to enhance the accuracies of ultra-rapid prediction clock offsets, the residuals are further modeled by a BP neural network.

As can be shown from Figure 4, there are differences in the significant periodic terms of three types of BDS satellites. The main significant periods of most GEO and IGSO clocks were about 24 h and 12 h, while that of MEO clocks were about 12 h and 6 h. Therefore, the corresponding period models in Table 2 were added to the basic prediction model shown in Equation (2). Then, the BDS satellite clock model can be presented as [14,15,23]:

$$y\left(t\right)=a_0+a_1\left(t_i-t_0\right)+a_2{\left(t_i-t_0\right)}^2+{\sum }_r^l{\Lambda }_r\sin \left[2\mathsf{\pi }{f}_r\left(t_i-t_0\right)+{\phi }_r\right]+{∆}_i,$$

(5)

where $l$ is the total number of period errors; ${\Lambda }_r$, $f_r$ and ${\phi }_r$ denote the amplitude, frequency, and phase of the clock offset period. $r$ is the number of the period.

4.2. Nonlinear Error Corrections by Using a BP Neural Network Model

By using a quadratic polynomial plus periodic term corrections model, the fitting residuals of the BDS clock offset series still contain various nonlinear colored noise (see Figure 6). The power spectral density function of colored noise is not constant [27,37]. However, the colored noise is irregular on the early performance and it is difficult to fit the conventional model effectively. There are five most significant noises, including random work frequency modulation (RWFM), flicker frequency modulation (FFM), white frequency modulation (WFM), flicker phase modulation (FPM), and white phase modulation (WPM) in the atomic clock offset sequences [23,27], and they cannot be effectively eliminated by the conventional fitting model. Therefore, a neural network of higher sensitivity and nonlinearity should be adopted to further compensate for the residuals. BP neural networks (BPNN) have strong a non-linear fitting ability which can map complex non-linear relationships. The learning rules of the BPNN are simple and easy to implement by computer. It has strong robustness, memory ability, nonlinear mapping ability, and a strong self-learning ability [38,39,40]. BPNNs can learn and store a large number of input, output, and feedback information [41,42,43]. The learning rule is to use the steepest descent method to continuously adjust the weights of the network by back propagation values and thresholds, so that the sum of the squares of the error of the network are at a minimum. A single BPNN which contains two layers is shown in Figure 8 [26,44].

As shown in Figure 8, the model needs input and output data to train the BPNN. Two days’ worth of clock offsets are used to fit and gain the BPNN model parameters. In this model, the input data is the first day residuals and the expectation output data is the second day residuals. The network process is mainly divided into two sections, the first one is the forward spread from the input layer through the hidden layer to the output layer; and the other is the error’s back propagation, which is contrary to the forward transmission steps [45,46,47]. Adjusting the weights and offsets by the back propagation errors [26,48], can be expressed by:

$$S_k={\displaystyle \sum }_{j=1}^l{\omega }_{jk}h\left(ne{t}_j\right)={\displaystyle \sum }_{j=1}^l{\omega }_{jk}g\left(\frac{{{\displaystyle \sum }}_{i=1}^n{\omega }_{ij}{x}_i-c_j}{d_j}\right)$$

(6)

where $i=1\cdots n,j=1\cdots l,k=1\cdots m$; $g\left(x\right)$ is the hidden layer driving function which adopt the sigmoid function and its expression is $g\left(x\right)=1/1+{\mathrm{e}}^{-x}$ [49,50,51,52]. $x_i$ is the neural network input values, which are the fitting residuals of the clock offset sequences in this paper, $x_i=\left[x_0,x_1,x_2,\cdots ,x_n\right]$. $n$, $l$, and $m$ are the number of input, hidden, and output layer, respectively [53,54,55]. As for the number of hidden layer neurons, if the number is larger, the network shows greater expressive ability. One and six neurons are selected for input and hidden layers in this study [26,54]. Since the output is the residual series of the clock offset, the output neuron is chosen as 1, using $g\left(x\right)$ to train the residual data, the error of hidden layer is $H_j$ and the error of output layer is $O_k$, which shown as Equations (7) and (8):

$$H_j=g\left({\displaystyle \sum }_{i=1}^n{\omega }_{ij}{x}_i-c_j\right)$$

(7)

$$O_k={\displaystyle \sum }_{j=1}^l{H}_j{\omega }_{jk}-d_j$$

(8)

where $w_{ij}$ and $w_{jk}$ are the weights of the input layer to the hidden layer and the hidden layer to the output layer. The parameters $c_j$ and $d_j$ are the dilation and the translation parameters of the node j in the hidden layer. The process of training a neural network involves tuning the values of the weights and biases of the network to optimize network performance, as defined by the network performance function [26,55,56]. The default performance function for feed-forward networks is the mean square error between the network’s outputs and the target outputs. This error is calculated as shown in Equation (9):

$$E=\frac{1}{2}{\displaystyle \sum }_{k=1}^m{\displaystyle \sum }_{n=1}^m{\left(Y_k-O_k\right)}^2=\frac{1}{2}{\displaystyle \sum }_{k=1}^m{\displaystyle \sum }_{n=1}^m{e}_k^2$$

(9)

where $Y_k$ is the actual output data, and the error between the actual output data and expected output data is $e_k$, $Y_k-O_k=e_k$. As the actual model error $E$ is calculated, the weights, dilation parameter and translation parameter are obtained [46]. Compared with the allowable error $\mathsf{\epsilon }$. If the actual model error $E$ is not smaller than the allowable error ε, the model error is corrected by $e_k$ so that the error of the model is further reduced until smaller than allow error $\mathsf{\epsilon }$. The values ${\omega }_{ij}$, ${\omega }_{ij}$ and $c_j$, $d_k$ are updated as shown in Equations (9) and (10):

$$\{\begin{array}{c}{\omega }_{ij}={\omega }_{ij}-\eta H_j\left(1-H_j\right) x_i{{\displaystyle \sum }}_{k=1}^m{\omega }_{jk}{e}_k+\alpha \\ {\omega }_{jk}={\omega }_{jk}-\eta H_j{e}_k\end{array}$$

(10)

$$\{\begin{array}{c}{c}_j=c_j-\eta H_j\left(1-H_j\right){{\displaystyle \sum }}_{k=1}^m{\omega }_{jk}{e}_k\\ d_k=d_k-\eta e_k\end{array}$$

(11)

The process of error back propagation makes the error function the minimum, $\mathrm{minE}$. If $\mathrm{minE}$ is less than the allowable error $\mathsf{\epsilon }$ or iterations have reached the pre-set number, the network comes to an end; otherwise, iteration continues [26]. $\eta$ is the learning rate which is the step size, generally taken as a constant between 0.1 and 0.4; and $\alpha$ is the coefficient correction constant, taken as a constant between 0.7 and 0.9 [26,36,41,45,46]. After the model training is completed, the fitting residuals of the clock offsets by the QP, BPNN, and two period models are shown in Figure 9.

As shown in Figure 9, the residuals by using the BPNN are significantly smaller than the fitting residuals without the BPNN (Figure 6). Thus, it is very effective for the BDS satellite clocks to achieve better fitting and forecasting accuracy. When the network weights and biases reach the allowable range, the BPNN training is completed [47,48,49,50,51,52]. However, the computation of the network is more complicated and its convergence rate will slow down. Moreover, it also makes the network easily over-trained, which leads to degradation of the network’s fault tolerance performance and generalizability [52,53]. Therefore, the number of iterations is set to a fixed value, which not only guarantees the solution time, but also prevents the impact of unsuccessful training [54,55,56,57]. Through combining the neural networks which have trained, the prediction model combines with Equation (5), which can be expressed as:

$$y\left(t\right)=a_0^p+a_1\left(t_i-t_0\right)+a_2{\left(t_i-t_0\right)}^2+{{\displaystyle \sum }}_k^l{\Lambda }_k\sin \left[2\mathsf{\pi }{f}_k\left(t_i-t_0\right)+{\phi }_k\right]+{{\displaystyle \sum }}_{j=1}^l{\omega }_{jk}h\left(\frac{{{\displaystyle \sum }}_{i=1}^n{\omega }_{ij}{x}_i-c_j}{d_j}\right)+{∆}_i,\overline{\text{P}},$$

(12)

Comparing with the basic model (2), for the proposed clock model a few periodic terms are introduced and the initial deviations are improved. In addition, the adaptive weight function of time factors and the nonlinear offset corrections are applied in the new model.

Then the predicted model and improved algorithms are illustrated. In order to understand the process of the clock offset prediction model, the diagram is shown in Figure 10.

As shown in Figure 10, the process steps of the BDS ultra-rapid clock offset prediction model are illustrated. Considering that the BDS satellite clock of GEO and IGSO characteristics are unstable, the forecasting model is divided into two parts. The first step uses a quadratic polynomial with a time-adaptive weight function addition periodic terms model. The second step uses a BP neural network to train the model. If the model is successfully trained, the neural network corrections will be added to the results of the first step prediction. Otherwise, the BP result are not added to the model, and only the initial deviation correction is amended.

Using the sequential adjustment method with the fixed length, Equation (12) can be processed for real-time clock fitting and predicting [14,15,16,26]. We use 48 h as the fixed length for fitting and 24 h as the fixed length for predicting.

4.3. Accuracy Assessment

The BDS ultra-rapid clock offset products of GBM and ISC can be downloaded from the public websites [57,58]. In order to verify the accuracy and applicability of the improved model, the observations and predictions of the BDS clock offset products were used to test and analyze. The time span of the data was from 1 January 2017 to 30 January 2017, with a sampling interval of 5 min.

The accuracy of the clock offset is described as the standard deviation (STD) ${\delta }^s$, the specific formula is:

$${\delta }^s=\sqrt{{\sum }_{i=1}^n{\left({∆}_i^s-\overline{{∆}^s}\right)}^2/n},$$

(13)

$$x_i={\sum }_{s=1}^{m_i}\left(t_i^s-t_{0i}^s\right)/m_i,$$

(14)

$${∆}_i^s=t_i^s-t_{0i}^s-x_i$$

(15)

where $i$ is the epoch of the clocks offset and $s$ is the satellite number. ${∆}_i^s=t_i^s-t_{0i}^s-x_i$ means the difference of the deviation between different reference clocks which is eliminated. $x_i$ is the difference between the clock offset of the real-time prediction and the precise observations. $t_i^s$ and $t_{0i}^s$ are the real-time prediction clock offsets and the precise observations of satellite $s$ in epoch $i$, $n$ is the number of the clock offset predictions, and $m_i$ is the satellite number of epoch $i$.

5. Numeral Experiments

5.1. Prediction Accuracies Analysis

The observations and predictions of the IGU and GBU clock products from 1 January 2017 to 30 January 2017 are downloaded to test the improved clock model. For comparing the accuracies of the improved model with ISU and GBU products, four schemes are designed and analyzed as follows:

• Scheme 1: Prediction clock offsets using the improved model with no BP corrections (no-BP);
• Scheme 2: Prediction clock offsets using the improved model with BP corrections (with-BP);
• Scheme 3: Prediction clock offsets from the ISU product (ISU-P) and GBU product (GBU-P); and
• Scheme 4: Prediction clock offsets only using the BP algorithm as reference [26].

By comparing with Scheme 1 and Scheme 2, the available of BP corrections can be proved. By comparing with Scheme 2 and Scheme 3, the improvement of the proposed model can be achieved. By comparing with Scheme 2 and Scheme 4, the enhanced level of the proposed model referred to the previous BP algorithm [26] can be verified.

The residuals of the BDS clock offset predictions obtained by the four schemes are shown in Figure 11 and Figure 12, respectively.

The average accuracy statistics of BDS clock offset predictions from the different schemes for 30 days are shown in

Table 3. The forecasting accuracy statistics of BDS satellite clock offsets for 30 days.

Time Length	GBU (ns)			ISU (ns)
	Scheme 3	Scheme 4	Scheme 2	Scheme 3	Scheme 4	Scheme 2
3 h	0.53	0.41	0.37	0.39	0.35	0.35
6 h	1.51	1.26	1.20	1.36	1.23	1.17
12 h	2.75	2.31	2.19	3.58	3.12	2.96
24 h	4.41	3.97	3.55	5.35	4.59	4.22

and Figure 13.

More analysis results of the above figures and tables will be discussed in Section 6.

5.2. Real-Time Precise Point Positioning Experiment

In order to verify the availability of the proposed clock model in the real-time precise point positioning (RTPPP), eight MGEX stations distributed around the Asia-Pacific region are selected and processed. The distribution of the selected MGEX stations is shown in Figure 14. The sampling interval of observations is 30 s and the observing time is 24 h. The ISU and GBU ultra-rapid predicting orbit products are selected to match the corresponding clock offset products. The main processing strategies of RTPPP experiment are as follows: First, the real-time orbit predictions of ISU-P and GBU-P are selected. Second, the clock predictions from ISU-P and GBU-P products and the proposed model are chosen separately. Third, the kinematic RTPPP results of eight stations which use different clock prediction products are computed. The positioning residuals of NNOR and PNGM stations are given in Figure 15 and Figure 16. The position accuracies of eight stations are achieved and shown in

Table 4. The position accuracy statistics.

Station Name	N (m)				E (m)				U (m)
	ISU-P	M1	GBU-P	M 1	ISU-P	M 1	GBU-P	M 1	ISU-P	M 1	GBU-P	M 1
HARB	0.096	0.085	0.085	0.077	0.095	0.071	0.097	0.081	0.157	0.101	0.203	0.139
MAL2	0.106	0.097	0.113	0.099	0.113	0.109	0.135	0.122	0.186	0.132	0.198	0.132
KRCH	0.084	0.079	0.096	0.081	0.096	0.081	0.112	0.105	0.174	0.119	0.251	0.146
JFNG	0.12	0.105	0.113	0.105	0.14	0.126	0.121	0.102	0.203	0.142	0.204	0.152
NRMG	0.057	0.049	0.063	0.056	0.071	0.065	0.065	0.052	0.196	0.153	0.189	0.113
KARR	0.046	0.041	0.053	0.049	0.063	0.061	0.051	0.043	0.179	0.127	0.174	0.097
NNOR	0.107	0.085	0.129	0.101	0.143	0.103	0.087	0.065	0.198	0.103	0.352	0.132
PNGM	0.075	0.059	0.097	0.079	0.067	0.059	0.127	0.099	0.173	0.135	0.352	0.098

¹ M means the modified model in this paper.

.

6. Discussion

The real-time prediction precision of on-board satellite atomic clocks is essential for GNSS navigation, positioning, and timing services. At present, few studies have assessed the BDS ultra-rapid clock offset model considering residual characteristics. We analyze the periodicity of the BDS satellite clock offsets and the characteristics of the fitting residual noises. In the end, an adaptive quadratic polynomial prediction model plus neural network and period items is constructed.

The orbital duration and on-board statistics of BDS satellites are given (Table 1). The periodic terms of satellites of the on-board clocks are matched using the FFT method (Table 2). The fitting residuals of the BDS clock offsets with quadratic polynomial and periodic terms are shown in Figure 6 and Figure 9. The proposed model improves the forecasting accuracy compared to that of ISU and GBU products (Figure 11, Figure 12 and Figure 13 and Table 3).

As shown in Figure 10 and Figure 11, the accuracies of GBU-P and ISU-P are slightly worse than that of Scheme 1. The improved model with a BP neural network (Table 3) is evidently superior to that of other schemes. For C14 in the GBU product and C06 in the ISU product, their predicting residuals enlarge rapidly with the increases in the length of the predicting times. However, the accuracies of C14 and C06 have been enhanced using the improved model, and their residuals are effectively controlled in the 24 h. Compared with the results of Table 2, the prediction accuracies of Table 3 have more advantages in long-term predictions more than in 3 h.

In order to further verify the stability and the precision of the proposed model in the long time scale, 30 days of real-time clock predictions are calculated. Based on the ultra-rapid observations of satellite clocks, the real-time predicted precisions of 3 h, 6 h, 12 h, and 24 h in every day are evaluated and compared with that of precise clock observations. The statistics of the average prediction results are calculated and the corresponding RMS are listed in Table 3.

As shown in Table 3 and Figure 13, the accuracies of ISU-P products are evidently superior to that of GBU-P products, because the ISU clock offset products are integration products of more than ten iGMAS analysis centers in China, which have greater robustness compared to ISU-P products. The average improvements using the proposed model in 3 h, 6 h, 12 h, and 24 h are 23.1%, 21.3%, 20.2%, and 19.8%, respectively. Meanwhile the accuracy improvements of the proposed model are 9.9%, 13.9%, 17.3%, and 21.2%, respectively, compared to GBU products.

As shown in Figure 15, Figure 16 and Table 4, compared with the results of the IGU-P and GBU-P clock product, the RTPPP precisions based on the proposed clock model have improved about 16%, 14%, and 38% in N, E, and U directions, respectively.

7. Conclusions

An improved prediction model for BDS satellite clocks is proposed in order to enhance the accuracies of ultra-rapid predicted clock offsets. The classified cyclic terms, time adaptive function, initial deviation, and BP neural network corrections are added in the proposed algorithm based on the quadratic polynomial model. The simulation results show that the performance and precision using the improved model are better than that of ISU products and GBU products. Some conclusions can be summarized as follows:

(1)

Compared to ISU-P products, the average improvements using the proposed model in 3 h, 6 h, 12 h, and 24 h are 23.1%, 21.3%, 20.2%, and 19.8%, respectively. Meanwhile the accuracy improvements of the proposed model are 9.9%, 13.9%, 17.3%, and 21.2% compared to GBU-P products.

(2)

The analyzed results of periodic terms show that the main significant periods of GEO and IGSO are 24 h and 12 h, while that of MEO are 12 h and 6 h. Specially, C11 has a significant periodic term of about 1.3 h, which is different from other MEOs. The first and second periodic terms both are evident and should be compensated in the BDS clock offsets prediction.

(3)

The fitting residuals show that, the accuracies of the old BDS satellites clocks are worse than that of other young satellites. Therefore, evidently, the performance of BDS satellite clocks may degrade during the increase in service years.

(4)

The RTPPP accuracies based on the proposed clock model are superior to 0.2 m and have improved about 16%, 14%, and 38% in N, E, and U directions, respectively.