Tropical Cyclone Rainfall Estimates from FY-3B MWRI Brightness Temperatures Using the WS Algorithm
Abstract
:1. Introduction
2. Instrument Description
3. Datasets and Processing
3.1. Brightness Temperature
3.2. GFS Environmental Product
3.3. NSIDC Rainfall Product
3.4. TRMM Precipitation Data
3.5. Data Matchup
4. Methodology
4.1. Microwave Radiation
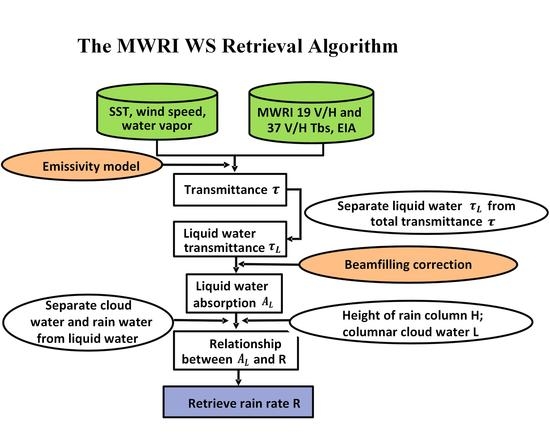
4.2. Retrieval Algorithm
5. Results
5.1. Comparison with the NSIDC rainfall product
5.2. Comparison with AMSR-E Tbs Retrievals
5.3. Case Study: Comparison with TRMM PR data for Maon
5.4. Mesoscale Structure of the Selected TCs
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gray, W.M. Global view of origin of tropical disturbances and storms. Mon. Weather Rev. 1968, 96, 669–700. [Google Scholar] [CrossRef]
- Cutter, S.L.; Emrich, C.T. Moral hazard, social catastrophe: The changing face of vulnerability along the hurricane coasts. Ann. Am. Acad. Political Soc. Sci. 2006, 604, 102–112. [Google Scholar] [CrossRef]
- Zick, S.E.; Matyas, C.J. A shape metric methodology for studying the evolving geometries of synoptic-scale precipitation patterns in tropical cyclones. Ann. Am. Assoc. Geogr. 2016, 106, 1217–1235. [Google Scholar] [CrossRef]
- Shige, S.; Takayabu, Y.N.; Tao, W.-K.; Johnson, D.E. Spectral retrieval of latent heating profiles from TRMM PR data. Part I: Development of a model-based algorithm. J. Appl. Meteorol. 2004, 43, 1095–1113. [Google Scholar] [CrossRef]
- Atlas, D.; Thiele, O.W. Precipitation Measurements from Space. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, NASA/Goddard Space Flight Center, Greenbelt MD, USA, 1 October 1981; p. 441. [Google Scholar]
- Milman, A.S.; Wilheit, T.T. Sea surface temperatures from the scanning multichannel microwave radiometer on Nimbus 7. J. Geophys. Res. 1985, 90, 11631. [Google Scholar] [CrossRef]
- Wentz, F.J.; Meissner, T. AMSR Ocean Algorithm Theoretical Basis Document, Version 2; Remote Sensing Systems: Santa Rosa, CA, USA, November 2000. [Google Scholar]
- Kidd, C.; Matsui, T.; Chern, J.; Mohr, K.; Kummerow, C.D.; Randel, D.L. Global precipitation estimates from cross-track passive microwave observations using a physically based retrieval scheme. J. Hydrometeorol. 2016, 17, 383–400. [Google Scholar] [CrossRef]
- Petković, V.; Kummerow, C.D.; Randel, D.L.; Pierce, J.R.; Kodros, J.K. Improving the quality of heavy precipitation estimates from satellite passive microwave rainfall retrievals. J. Hydrometeorol. 2018, 19, 69–85. [Google Scholar] [CrossRef]
- Kidd, C.; Levizzani, V. Status of satellite precipitation retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef] [Green Version]
- Basharinov, A.; Yegorov, S.; Gurvich, A.; Oboukhov, A. Some results of microwave sounding of the atmosphere and ocean from the satellite Cosmos 243. Space Res. 1971, 11, 593–600. [Google Scholar]
- Hollinger, J.P.; Peirce, J.L.; Poe, G.A. SSM/I instrument evaluation. IEEE Trans. Geosci. Remote Sens. 1990, 28, 781–790. [Google Scholar] [CrossRef]
- Wentz, F.J.; Spencer, R.W. SSM/I rain retrievals within a unified all-weather ocean algorithm. J. Atmos. Sci. 1998, 55, 1613–1627. [Google Scholar] [CrossRef]
- Kummerow, C.D.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef] [Green Version]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Xie, P. NASA Global Precipitation Measurement Integrated Multi-Satellite Retrievals for GPM (IMERG) Algorithm Theoretical Basis Document (ATBD) Version 4.5; National Aeronautics and Space Administration: Washington, DC, USA, November 2015. [Google Scholar]
- Kawanishi, T.; Sezai, T.; Ito, Y.; Imaoka, K.; Takeshima, T.; Ishido, Y.; Shibata, A.; Miura, M.; Inahata, H.; Spencer, R.W. The Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E), NASDA’s contribution to the EOS for global energy and water cycle studies. IEEE Trans. Geosci. Remote Sens. 2003, 41, 184–194. [Google Scholar] [CrossRef]
- Yang, H.; Weng, F.; Lv, L.; Lu, N.; Liu, G.; Bai, M.; Qian, Q.; He, J.; Xu, H. The FengYun-3 Microwave Radiation Imager on-orbit verification. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4552–4560. [Google Scholar] [CrossRef]
- Buettner, K.J.K. Regenortung vom wettersatelliten mit hilfe von zentimeterwellen (Rain localization from a weather satellite via centimeter waves). Naturwiss 1963, 50, 591–592. [Google Scholar] [CrossRef]
- Grody, N.C. Classification of snow cover and precipitation using the Special Sensor Microwave Imager. J. Geophys. Res. Atmos. 1991, 96, 7423–7435. [Google Scholar] [CrossRef]
- Ferraro, R.R.; Marks, G.F. The development of SSM/I rain-rate retrieval algorithms using ground-based radar measurements. J. Atmos. Ocean. Technol. 1995, 12, 755–770. [Google Scholar] [CrossRef]
- Spencer, R.W.; Goodman, H.M.; Hood, R.E. Precipitation retrieval over land and ocean with the SSM/I: Identification and characteristics of the scattering signal. J. Atmos. Ocean. Technol. 1989, 6, 254–273. [Google Scholar] [CrossRef]
- Kidd, C. On rainfall retrieval using polarization-corrected temperatures. Int. J. Remote Sens. 1998, 19, 981–996. [Google Scholar] [CrossRef]
- Brown, P.J.; Kummerow, C.D.; Randel, D.L. Hurricane GPROF: An optimized ocean microwave rainfall retrieval for tropical cyclones. J. Atmos. Ocean. Technol. 2016, 33, 1539–1556. [Google Scholar] [CrossRef]
- Hilburn, K.A.; Wentz, F.J. Intercalibrated passive microwave rain products from the Unified Microwave Ocean Retrieval Algorithm (UMORA). J. Appl. Metrorol. Climatol. 2008, 47, 778–794. [Google Scholar] [CrossRef]
- Kummerow, C.D.; Hong, Y.; Olson, W.S.; Yang, S.; Adler, R.F.; McCollum, J.; Ferraro, R.; Petty, G.; Shin, D.B.; Wilheit, T.T. The evolution of the Goddard profiling algorithm (GPROF) for rainfall estimation from passive microwave sensors. J. Appl. Meteorol. 2001, 40, 1801–1820. [Google Scholar] [CrossRef]
- Kummerow, C.D.; Randel, D.L.; Kulie, M.; Wang, N.Y.; Ferraro, R.; Munchak, S.J.; Petkovic, V. The evolution of the Goddard Profiling Algorithm to a fully parametric scheme. J. Atmos. Ocean. Technol. 2015, 32, 2265–2280. [Google Scholar] [CrossRef]
- Kummerow, C.D.; Ringerud, S.; Crook, J.; Randel, D.; Berg, W. An observationally generated a priori database for microwave rainfall retrievals. J. Atmos. Ocean. Technol. 2011, 28, 113–130. [Google Scholar] [CrossRef]
- Wilheit, T.; Kummerow, C.D.; Ferraro, R. Rainfall algorithms for AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 204–214. [Google Scholar] [CrossRef]
- Li, X.; Zhao, F. Characteristics of precipitating clouds in typhoon Ma-on from MWRI and TMI observations. In Proceedings of the Remote Sensing, Environment and Transportation Engineering (RSETE), Nanjing, China, 1–3 June 2012; pp. 1–4. [Google Scholar]
- Zhang, R.; Wang, Z.; Zhang, L.; Li, Y. Rainfall retrieval of tropical cyclones using FY-3B microwave radiation imager (MWRI). In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 550–553. [Google Scholar]
- Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The international best track archive for climate stewardship (IBTrACS) unifying tropical cyclone data. Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
- Liu, C.; Zipser, E.J.; Cecil, D.J.; Nesbitt, S.W.; Sherwood, S. A cloud and precipitation feature database from nine years of TRMM observations. J. Appl. Metrorol. Climatol. 2008, 47, 2712–2728. [Google Scholar] [CrossRef]
- Viltard, N.; Burlaud, C.; Kummerow, C.D. Rain retrieval from TMI brightness temperature measurements using a TRMM PR–based database. J. Appl. Metrorol. Climatol. 2006, 45, 455–466. [Google Scholar] [CrossRef]
- Kummerow, C.D.; Olson, W.S.; Giglio, L. A simplified scheme for obtaining precipitation and vertical hydrometeor profiles from passive microwave sensors. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1213–1232. [Google Scholar] [CrossRef]
- Yang, H.; Zou, X.; Li, X.; You, R. Environmental data records from FengYun-3B Microwave Radiation Imager. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4986–4993. [Google Scholar] [CrossRef]
- Wolff, D.B.; Fisher, B.L. Assessing the relative performance of microwave-based satellite rain-rate retrievals using TRMM ground validation data. J. Appl. Metrorol. Climatol. 2009, 48, 1069–1099. [Google Scholar] [CrossRef]
- Islam, T.; Rico-Ramirez, M.A.; Han, D.; Srivastava, P.K. Using S-band dual polarized radar for convective/stratiform rain indexing and the correspondence with AMSR-E GSFC profiling algorithm. Adv. Space Res. 2012, 50, 1383–1390. [Google Scholar] [CrossRef]
- Iguchi, T.; Kozu, T.; Meneghini, R.; Awaka, J.; Okamoto, K.I. Rain-profiling algorithm for the TRMM precipitation radar. J. Appl. Meteorol. 2000, 39, 2038–2052. [Google Scholar] [CrossRef]
- Shige, S.; Takayabu, Y.N.; Tao, W.K.; Shie, C.L. Spectral retrieval of latent heating profiles from TRMM PR data. Part II: Algorithm improvement and heating estimates over Tropical Ocean regions. J. Appl. Metrorol. Climatol. 2007, 46, 1098–1124. [Google Scholar] [CrossRef]
- Seto, S.; Iguchi, T.; Utsumi, N.; Kiguchi, M.; Oki, T. Evaluation of extreme rain estimates in the TRMM/PR standard product version 7 using high-temporal-resolution rain gauge datasets over Japan. SOLA 2013, 9, 98–101. [Google Scholar] [CrossRef]
- Kirstetter, P.-E.; Hong, Y.; Gourley, J.J.; Schwaller, M.; Petersen, W.; Zhang, J. Comparison of TRMM 2A25 products, version 6 and version 7, with NOAA/NSSL ground radar–based National Mosaic QPE. J. Hydrometeorol. 2013, 14, 661–669. [Google Scholar] [CrossRef]
- Tu, J.Y.; Chou, C.; Chu, P.S. The abrupt shift of typhoon activity in the vicinity of taiwan and its association with western North Pacific-East Asian climate change. J. Clim. 2009, 22, 3617–3628. [Google Scholar] [CrossRef]
- Shibata, A. A wind speed retrieval algorithm by combining 6 and 10 GHz data from Advanced Microwave Scanning Radiometer: Wind speed inside hurricanes. J. Oceanogr. 2006, 62, 351–359. [Google Scholar] [CrossRef]
- Yin, X.; Wang, Z.; Song, Q.; Huang, Y.; Zhang, R. Estimate of ocean wind vectors inside tropical cyclones from polarimetric radiometer. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1701–1714. [Google Scholar] [CrossRef]
- Wentz, F.J. A well-calibrated ocean algorithm for Special Sensor Microwave/Imager. J. Geophys. Res. Oceans 1997, 102, 8703–8718. [Google Scholar] [CrossRef]
- Petković, V.; Kummerow, C.D. Understanding the sources of satellite passive microwave rainfall retrieval systematic errors over land. J. Appl. Metrorol. Climatol. 2017, 56, 597–614. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.J. Wind-vector retrievals under rain with passive satellite microwave radiometers. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3065–3083. [Google Scholar] [CrossRef]
- Ulaby, F.T. Microwave Remote Sensing Active and Passive-Volume III: From Theory to Applications; Artech House: Dedham, MA, USA, 1986. [Google Scholar]
- Houze, R.A., Jr. Clouds in tropical cyclones. Mon. Weather Rev. 2010, 138, 293–344. [Google Scholar] [CrossRef]












| Frequency (GHz) | 10.65 | 18.7 | 23.8 | 36.5 | 89.0 |
|---|---|---|---|---|---|
| Polarization | V/H | V/H | V/H | V/H | V/H |
| Resolution (km) | 51 × 85 | 30 × 50 | 27 × 45 | 18 × 30 | 9 × 15 |
| Sensitivity (K) | 0.5 | 0.5 | 0.5 | 0.5 | 0.8 |
| Calibration error (K) | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
| Swath width | 1400 km | ||||
| Scan mode | Conical scanning | ||||
| Scan cycle | 1.8 s | ||||
| Viewing angle | 45o | ||||
| Samples | 254 | ||||
| Sampling interval | 2.08 ms | ||||
| TC’s Name | Date | Matched Point Number |
|---|---|---|
| Songda | 17:25, 27 May 2011 | 18,263 |
| Maon | 03:53, 17 July 2011 | 19,234 |
| Mufia | 17:21, 4 August 2011 | 15,153 |
| Talas | 04:19, 27 August 2011 | 14,095 |
| Sonca | 16:07, 19 September 2011 | 21,852 |
| Nesat | 05:53, 28 September 2011 | 13,282 |
| Total number of matched pixels: 101,879 | ||
| Rain Interval | Pixel Number | MWRI Retrievals | NSIDC Rain Rate | Bias | Bias Percentage |
|---|---|---|---|---|---|
| 0.0–0.5 | 55,172 | 0.11 | 0.14 | −0.03 | −21.4% |
| 0.5–1.0 | 10,794 | 0.65 | 0.71 | −0.06 | −8.4% |
| 1.0–2.0 | 7711 | 1.46 | 1.43 | 0.03 | 2.1% |
| 2.0–3.0 | 4555 | 2.57 | 2.48 | 0.09 | 3.6% |
| 3.0–4.0 | 3500 | 3.35 | 3.47 | −0.12 | −3.4% |
| 4.0–6.0 | 4076 | 4.18 | 4.87 | −0.69 | −14.1% |
| 6.0–8.0 | 2445 | 6.17 | 6.94 | −0.77 | −11.1% |
| 8.0–10.0 | 1671 | 8.34 | 8.95 | −0.71 | −7.9% |
| 10.0–15.0 | 2356 | 12.07 | 12.21 | −0.14 | −1.1% |
| 15.0–25.0 | 1629 | 16.80 | 18.40 | −1.60 | −8.7% |
| 25.0–30.0 | 237 | 21.00 | 27.20 | −6.20 | −22.8% |
| Total bias: −0.14 | Total RMSE: 1.99 | ||||
| TC’s Name | MWRI | AMSR-E | ||
|---|---|---|---|---|
| Bias | RMSE | Bias | RMSE | |
| Songda | 0.01 | 2.52 | 1.11 | 3.63 |
| Maon | −0.33 | 1.23 | 0.51 | 2.48 |
| Mufia | −0.25 | 1.99 | 0.73 | 3.22 |
| Talas | −0.36 | 1.97 | 0.85 | 2.84 |
| Sonca | 0.09 | 0.98 | 0.65 | 2.00 |
| Nesat | −0.21 | 2.99 | 1.74 | 4.49 |
| Total | −0.14 | 1.99 | 0.90 | 3.11 |
| Rain Interval | Pixel Number | PR Rain Rate | MWRI | NSIDC | ||
|---|---|---|---|---|---|---|
| Rain Rate | Bias | Rain Rate | Bias | |||
| 0.0–0.5 | 797 | 0.18 | 0.73 | 0.55 | 0.99 | 0.81 |
| 0.5–1.0 | 338 | 0.74 | 1.91 | 1.17 | 2.34 | 1.60 |
| 1.0–2.0 | 420 | 1.47 | 2.89 | 1.42 | 3.69 | 2.22 |
| 2.0–3.0 | 248 | 2.50 | 3.76 | 1.26 | 4.56 | 2.06 |
| 3.0–4.0 | 201 | 3.47 | 4.90 | 1.43 | 5.78 | 2.31 |
| 4.0–6.0 | 295 | 4.89 | 5.25 | 0.34 | 6.26 | 1.37 |
| 6.0–8.0 | 53 | 7.42 | 6.27 | −1.15 | 8.43 | 1.01 |
| 8.0–10.0 | 17 | 9.48 | 5.73 | −3.75 | 9.20 | −0.28 |
| 10.0–25.0 | 27 | 13.76 | 4.97 | −8.79 | 7.34 | −6.42 |
| Total bias: | 0.74 | 1.41 | ||||
| Total RMSE: | 2.40 | 2.64 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Wang, Z.; Hilburn, K.A. Tropical Cyclone Rainfall Estimates from FY-3B MWRI Brightness Temperatures Using the WS Algorithm. Remote Sens. 2018, 10, 1770. https://doi.org/10.3390/rs10111770
Zhang R, Wang Z, Hilburn KA. Tropical Cyclone Rainfall Estimates from FY-3B MWRI Brightness Temperatures Using the WS Algorithm. Remote Sensing. 2018; 10(11):1770. https://doi.org/10.3390/rs10111770
Chicago/Turabian StyleZhang, Ruanyu, Zhenzhan Wang, and Kyle A. Hilburn. 2018. "Tropical Cyclone Rainfall Estimates from FY-3B MWRI Brightness Temperatures Using the WS Algorithm" Remote Sensing 10, no. 11: 1770. https://doi.org/10.3390/rs10111770
APA StyleZhang, R., Wang, Z., & Hilburn, K. A. (2018). Tropical Cyclone Rainfall Estimates from FY-3B MWRI Brightness Temperatures Using the WS Algorithm. Remote Sensing, 10(11), 1770. https://doi.org/10.3390/rs10111770