Confronting Soil Moisture Dynamics from the ORCHIDEE Land Surface Model With the ESA-CCI Product: Perspectives for Data Assimilation
Abstract
:1. Introduction
- How should the satellite product be processed (bias corrected) for a meaningful comparison with the ORCHIDEE LSM?
- What are the impacts of the selected model representative soil depth and the meteorological forcing on the comparison between the satellite and model SSM?
- What are the strengths and weaknesses of a few (widely used) temporal comparison metrics? What is the potential of these metrics for future model structure/parameter optimization?
2. Methods and Data
2.1. The ORCHIDEE Land-Surface Model
2.2. ESA-CCI SM Product
2.3. Simulation Set Up
2.3.1. ORCHIDEE Configurations
2.3.2. Meteorological Forcing
2.3.3. Land Cover
2.3.4. Model Spin Up
2.3.5. Model Data Comparison
2.3.6. Performed Simulations
2.4. Data Processing and Statistical Analysis
2.4.1. Statistically Rescaling and Bias Correcting the Observations
2.4.2. Seasonal and Inter-Annual Variability
- a slow-varying component (SC) which represents seasonal variability. This is calculated in two steps. First, the mean annual cycle over the 8 years of data is calculated (). Then, following [55], the signal is averaged using a 35-day moving window. Considering a 35-day period , a minimum of 5 values are needed to calculate the average soil moisture for this period resulting in the slow-varying component:When there are not 5 values within P for a given grid point, the grid point is then ignored for that given period.
- a fast-varying component (FC), or daily anomaly, given by:
2.4.3. Correlation Scores
2.4.4. Root Mean Standard Deviation
2.4.5. MSD Decomposition
2.4.6. Autocorrelation and Lag Time
2.4.7. Singular Value Decomposition
3. Results
3.1. Rescaling the ESA-CCI SM Product
3.2. An Analysis of Model Depth Selection
3.3. Mean Temporal Correlations between Model and ESA-CCI SM Product
3.4. The Effect of Meteorological and Land Cover Forcing Data
3.5. Measuring the Covariance of Rainfall and Soil Moisture
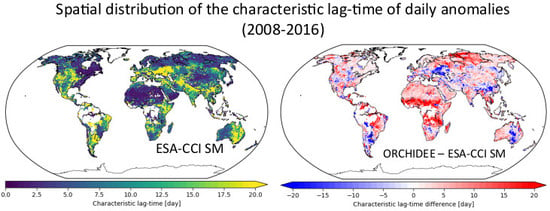
3.6. Temporal Autocorrelation
3.7. Potential Impact of Parameterization on SM Dynamics
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| 90 N–60 N | 60 N–30 N | 30 N–0 | 0–30 S | 30 S–30 N | |
|---|---|---|---|---|---|
| Jan–Mar | 34 | 10,662 | 9398 | 6543 | 1874 |
| Apr–Jun | 9212 | 19,385 | 9578 | 6531 | 1866 |
| Jul–Sep | 9597 | 19,456 | 9557 | 6501 | 1820 |
| Oct–Dec | 3310 | 17,003 | 9545 | 6528 | 1865 |
| Index | Range Covered | % of Points | r | RMSD | (Mod) | (Mod-Obs) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| REF | NoRs | REF | NoRs | REF | NoRs | REF | NoRs | REF | NoRs | ||
| 1 | 29.0 | 25.0 | 0.47 | 0.37 | 0.029 | 0.033 | 9.605 | 6.744 | 4.859 | 1.969 | |
| 2 | 28.0 | 27.0 | 0.46 | 0.38 | 0.038 | 0.049 | 12.14 | 8.017 | 2.768 | −0.760 | |
| 3 | 23.0 | 25.0 | 0.51 | 0.47 | 0.037 | 0.046 | 11.841 | 9.711 | 1.744 | −0.244 | |
| 4 | 18.0 | 21.0 | 0.67 | 0.68 | 0.038 | 0.043 | 14.943 | 12.631 | 1.796 | −0.166 | |
| 1 | Coarse | 25.0 | 25.0 | 0.50 | 0.46 | 0.028 | 0.029 | 8.217 | 5.719 | 2.756 | 0.254 |
| 2 | Medium | 62.0 | 62.0 | 0.49 | 0.44 | 0.037 | 0.049 | 12.392 | 9.734 | 2.768 | 0.111 |
| 3 | Fine | 11.0 | 11.0 | 0.68 | 0.65 | 0.038 | 0.042 | 17.380 | 13.497 | 4.207 | 0.350 |

References
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Booth, B.B.; Jones, C.D.; Collins, M.; Totterdell, I.J.; Cox, P.M.; Sitch, S.; Huntingford, C.; Betts, R.A.; Harris, G.R.; Lloyd, J. High sensitivity of future global warming to land carbon cycle processes. Environ. Res. Lett. 2012, 7, 024002. [Google Scholar] [CrossRef] [Green Version]
- Le Quéré, C.; Moriarty, R.; Andrew, R.M.; Peters, G.P.; Ciais, P.; Friedlingstein, P.; Jones, S.D.; Sitch, S.; Tans, P.; Arneth, A.; et al. Global carbon budget 2014. Earth Syst. Sci. Data 2015, 7, 47–85. [Google Scholar] [CrossRef] [Green Version]
- Anav, A.; Friedlingstein, P.; Beer, C.; Ciais, P.; Harper, A.; Jones, C.; Murray-Tortarolo, G.; Papale, D.; Parazoo, N.C.; Peylin, P.; et al. Spatiotemporal patterns of terrestrial gross primary production: A review. Rev. Geophys. 2015, 53, 785–818. [Google Scholar] [CrossRef] [Green Version]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Haerter, J.O.; Hagemann, S.; Piani, C. On the contribution of statistical bias correction to the uncertainty in the projected hydrological cycle. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W.; Hasenauer, S.; Hahn, S. Assimilation of surface-and root-zone ASCAT soil moisture products into rainfall–runoff modeling. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2542–2555. [Google Scholar] [CrossRef]
- Miralles, D.; Van Den Berg, M.; Teuling, A.; De Jeu, R. Soil moisture-temperature coupling: A multiscale observational analysis. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Taylor, C.M.; De Jeu, R.A.; Guichard, F.; Harris, P.P.; Dorigo, W.A. Afternoon rain more likely over drier soils. Nature 2012, 489, 423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pitman, A.; Henderson-Sellers, A.; Desborough, C.; Yang, Z.L.; Abramopoulos, F.; Boone, A.; Dickinson, R.; Gedney, N.; Koster, R.; Kowalczyk, E.; et al. Key results and implications from phase 1 (c) of the project for intercomparison of land-surface parametrization schemes. Clim. Dyn. 1999, 15, 673–684. [Google Scholar] [CrossRef]
- Guimberteau, M.; Zhu, D.; Maignan, F.; Huang, Y.; Chao, Y.; Dantec-Nédélec, S.; Ottlé, C.; Jornet-Puig, A.; Bastos, A.; Laurent, P.; et al. ORCHIDEE-MICT (v8. 4.1), a land surface model for the high latitudes: Model description and validation. Geosci. Model Dev. 2018, 11, 121. [Google Scholar] [CrossRef]
- Rebel, K.; De Jeu, R.; Ciais, P.; Viovy, N.; Piao, S.; Kiely, G.; Dolman, A. A global analysis of soil moisture derived from satellite observations and a land surface model. Hydrol. Earth Syst. Sci. 2012, 16, 833–847. [Google Scholar] [CrossRef] [Green Version]
- Ngo-Duc, T.; Laval, K.; Ramillien, G.; Polcher, J.; Cazenave, A. Validation of the land water storage simulated by Organising Carbon and Hydrology in Dynamic Ecosystems (ORCHIDEE) with Gravity Recovery and Climate Experiment (GRACE) data. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Swenson, S.; Lawrence, D. Assessing a dry surface layer-based soil resistance parameterization for the Community Land Model using GRACE and FLUXNET-MTE data. J. Geophys. Res. Atmos. 2014, 119, 10299–10312. [Google Scholar] [CrossRef]
- Ahmed, M.; Sultan, M.; Yan, E.; Wahr, J. Assessing and improving land surface model outputs over Africa using GRACE, field, and remote sensing data. Surv. Geophys. 2016, 37, 529–556. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements ofthe global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef] [Green Version]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Bartalis, Z.; Wagner, W.; Naeimi, V.; Hasenauer, S.; Scipal, K.; Bonekamp, H.; Figa, J.; Anderson, C. Initial soil moisture retrievals from the METOP-A Advanced Scatterometer (ASCAT). Geophys. Res. Lett. 2007, 34, 5–9. [Google Scholar] [CrossRef]
- Fascetti, F.; Pierdicca, N.; Pulvirenti, L.; Crapolicchio, R.; Muñoz-Sabater, J. A comparison of ASCAT and SMOS soil moisture retrievals over Europe and Northern Africa from 2010 to 2013. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 135–142. [Google Scholar] [CrossRef]
- Crow, W.; Chen, F.; Reichle, R.; Xia, Y.; Liu, Q. Exploiting Soil Moisture, Precipitation, and Streamflow Observations to Evaluate Soil Moisture/Runoff Coupling in Land Surface Models. Geophys. Res. Lett. 2018, 45, 4869–4878. [Google Scholar] [CrossRef] [PubMed]
- Al-Yaari, A.; Wigneron, J.P.; Ducharne, A.; Kerr, Y.; De Rosnay, P.; De Jeu, R.; Govind, A.; Al Bitar, A.; Albergel, C.; Munoz-Sabater, J.; et al. Global-scale evaluation of two satellite-based passive microwave soil moisture datasets (SMOS and AMSR-E) with respect to Land Data Assimilation System estimates. Remote Sens. Environ. 2014, 149, 181–195. [Google Scholar] [CrossRef] [Green Version]
- Francois, C.; Quesney, A.; Ottlé, C. Sequential assimilation of ERS-1 SAR data into a coupled land surface–hydrological model using an extended Kalman filter. J. Hydrometeorol. 2003, 4, 473–487. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Parinussa, R.M.; Dorigo, W.A.; De Jeu, R.A.M.; Wagner, W.; van Dijk, A.I.J.M.; McCabe, M.F.; Evans, J.P. Developing an improved soil moisture dataset by blending passive and active microwave satellite-based retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 425–436. [Google Scholar] [CrossRef] [Green Version]
- De Lannoy, G.J.; Reichle, R.H. Assimilation of SMOS brightness temperatures or soil moisture retrievals into a land surface model. Hydrol. Earth Syst. Sci. 2016, 20, 4895. [Google Scholar] [CrossRef]
- Yang, K.; Zhu, L.; Chen, Y.; Zhao, L.; Qin, J.; Lu, H.; Tang, W.; Han, M.; Ding, B.; Fang, N. Land surface model calibration through microwave data assimilation for improving soil moisture simulations. J. Hydrol. 2016, 533, 266–276. [Google Scholar] [CrossRef]
- Kolassa, J.; Reichle, R.; Draper, C. Merging active and passive microwave observations in soil moisture data assimilation. Remote Sens. Environ. 2017, 191, 117–130. [Google Scholar] [CrossRef]
- Pinnington, E.; Quaife, T.; Black, E. Impact of remotely sensed soil moisture and precipitation on soil moisture prediction in a data assimilation system with the JULES land surface model. Hydrol. Earth Syst. Sci. 2018, 22, 2575–2588. [Google Scholar] [CrossRef] [Green Version]
- Bolten, J.D.; Crow, W.T.; Zhan, X.; Jackson, T.J.; Reynolds, C.A. Evaluating the utility of remotely sensed soil moisture retrievals for operational agricultural drought monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 57–66. [Google Scholar] [CrossRef]
- Scholze, M.; Buchwitz, M.; Dorigo, W.; Guanter, L.; Quegan, S. Reviews and syntheses: Systematic Earth observations for use in terrestrial carbon cycle data assimilation systems. Biogeosciences 2017, 14, 3401. [Google Scholar] [CrossRef]
- Vrugt, A.; Diks, G.H.; Gupta, V.; Bouten, W.; Verstraten, M. Improved treatment of uncertainty in hydrologic modeling: Combining the strengths of global optimization and data assimilation. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef] [Green Version]
- Ajami, K.; Qingyun, D.; Soroosh, S. An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Yin, J.; Zhan, X.; Zheng, Y.; Liu, J.; Fang, L.; Hain, C.R. Enhancing model skill by assimilating SMOPS blended soil moisture product into Noah land surface model. J. Hydrometeorol. 2015, 16, 917–931. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Dorigo, W.A.; Parinussa, R.M.; De Jeu, R.A.M.; Wagner, W.; McCabe, M.F.; Evans, J.P.; Van Dijk, A.I.J.M. Trend-preserving blending of passive and active microwave soil moisture retrievals. Remote Sens. Environ. 2012, 123, 280–297. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Gruber, A.; De Jeu, R.A.M.; Wagner, W.; Stacke, T.; Loew, A.; Albergel, C.; Brocca, L.; Chung, D.; Parinussa, R.M.; et al. Evaluation of the ESA CCI soil moisture product using ground-based observations. Remote Sens. Environ. 2015, 162, 380–395. [Google Scholar] [CrossRef]
- Albergel, C.; Dorigo, W.; Reichle, R.; Balsamo, G.; De Rosnay, P.; Muñoz-Sabater, J.; Isaksen, L.; De Jeu, R.; Wagner, W. Skill and global trend analysis of soil moisture from reanalyses and microwave remote sensing. J. Hydrometeorol. 2013, 14, 1259–1277. [Google Scholar] [CrossRef]
- Krinner, G.; Viovy, N.; de Noblet-Ducoudré, N.; Ogée, J.; Polcher, J.; Friedlingstein, P.; Ciais, P.; Sitch, S.; Prentice, I.C. A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system. Glob. Biogeochem. Cycles 2005, 19, 1–33. [Google Scholar] [CrossRef]
- De Rosnay, P.; Bruen, M.; Polcher, J. Sensitivity of surface fluxes to the number of layers in the soil model used in GCMs. Geophys. Res. Lett. 2000, 27, 3329–3332. [Google Scholar] [CrossRef] [Green Version]
- De Rosnay, P.; Polcher, J.; Bruen, M.; Laval, K. Impact of a physically based soil water flow and soil-plant interaction representation for modeling large-scale land surface processes. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef]
- D’Orgeval, T.; Polcher, J.; De Rosnay, P. Sensitivity of the West African hydrological cycle in ORCHIDEE to infiltration processes. Hydrol. Earth Syst. Sci. 2008, 12, 1387–1401. [Google Scholar] [CrossRef] [Green Version]
- Ducharne, A.; Ottlé, C.; Maignan, F.; Vuichard, N.; Ghattas, J.; Wang, F.; Peylin, P.; Polcher, J.; Guimberteau, M.; Maugis, P.; et al. The Hydrol Module of ORCHIDEE: Scientific Documentation [Rev 3977] and On, Work in Progress, Towards CMIP6v1; Technical Report; Institut Pierre Simon Laplace: Paris, France, 2017. [Google Scholar]
- Wagner, W.; Dorigo, W.; de Jeu, R.; Fernandez, D.; Benveniste, J.; Haas, E.; Ertl, M. Fusion of active and passive microwave observations to create an essential climate variable data record on soil moisture. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. (ISPRS Ann.) 2012, 7, 315–321. [Google Scholar] [CrossRef]
- Owe, M.; De Jeu, R.; Holmes, T. Multisensor historical climatology of satellite-derived global land surface moisture. J. Geophys. Res. Earth Surf. 2008, 113, 1–17. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A method for estimating soil moisture from ERS scatterometer and soil data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soci. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Sellers, P.J.; Heiser, M.D.; Hall, F.G. Relations between surface conductance and spectral vegetation indices at intermediate (100 m2 to 15 km2) length scales. J. Geophys. Res. Atmos. 1992, 97, 19033–19059. [Google Scholar] [CrossRef]
- CERA-SAT ECMWF Archived Dataset. Available online: https://www.ecmwf.int/en/forecasts/datasets/archive-datasets/reanalysis-datasets/cera-sat (accessed on 29 May 2018).
- New, M.; Hulme, M.; Jones, P. Representing twentieth-century space–time climate variability. Part II: Development of 1901–96 monthly grids of terrestrial surface climate. J. Clim. 2000, 13, 2217–2238. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soci. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef] [Green Version]
- Poulter, B.; MacBean, N.; Hartley, A.; Khlystova, I.; Arino, O.; Betts, R.; Bontemps, S.; Boettcher, M.; Brockmann, C.; Defourny, P.; et al. Plant functional type classification for earth system models: Results from the European Space Agency’s Land Cover Climate Change Initiative. Geosci. Model Dev. 2015, 8, 2315–2328. [Google Scholar] [CrossRef]
- Bontemps, S.; Boettcher, M.; Brockmann, C.; Kirches, G.; Lamarche, C.; Radoux, J.; Santoro, M.; Van Bogaert, E.; Wegmüller, U.; Herold, M.; et al. Multi-Year Global Land Cover Mapping at 300 M and Characterization for Climate Modelling: Achievements of the Land Cover Component of the Esa Climate Change Initiative. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 323–328. [Google Scholar] [CrossRef]
- Scipal, K.; Drusch, M.; Wagner, W. Assimilation of a ERS scatterometer derived soil moisture index in the ECMWF numerical weather prediction system. Adv. Water Resour. 2008, 31, 1101–1112. [Google Scholar] [CrossRef]
- Paulik, C.; Plocon, A.; Hahn, S.; Mistelbauer, T.; Schmitzer, M.; Alegrub88; iteubner.; Reimer, C. TUW-GEO/Pytesmo: V0.6.10; TU Wein: Vienna, Austria, 2018. [Google Scholar] [CrossRef]
- Albergel, C.; Rüdiger, C.; Pellarin, T.; Calvet, J.C.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B.; Martin, E. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. Discuss. 2008, 12, 1323–1337. [Google Scholar] [CrossRef]
- Kobayashi, K.; Salam, M.U. Comparing simulated and measured values using mean squared deviation and its components. Agron. J. 2000, 92, 345–352. [Google Scholar] [CrossRef]
- Delworth, T.L.; Manabe, S. The Influence of Potential Evaporation on the Variabilities of Simulated Soil Wetness and Climate. Am. Meteorol. Soc. 1988. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Smith, C.; Wallace, J.M. An Intercomparison of Methods for Finding Coupled Patterns in Climate Data. Am. Meteorol. Soc. 1992. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Martens, B.; Miralles, D.G.; Lievens, H.; van der Schalie, R.; De Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E.C. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Albergel, C.; Munier, S.; Leroux, D.J.; Dewaele, H.; Fairbairn, D.; Barbu, A.L.; Gelati, E.; Dorigo, W.; Faroux, S.; Meurey, C.; et al. Sequential assimilation of satellite-derived vegetation and soil moisture products using SURFEX_v8.0: LDAS-Monde assessment over the Euro-Mediterranean area. Geosci. Model Dev. 2017, 10, 3889–3912. [Google Scholar] [CrossRef] [Green Version]
- Entekhabi, D.; Reichle, R.H.; Koster, R.D.; Crow, W.T. Performance metrics for soil moisture retrievals and application requirements. J. Hydrometeorol. 2010, 11, 832–840. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Wagner, W.; Naeimi, V.; Bartalis, Z.; Hasenauer, S. Improving runoff prediction through the assimilation of the ASCAT soil moisture product. Hydrol. Earth Syst. Sci. 2010, 14, 1881–1893. [Google Scholar] [CrossRef] [Green Version]
- Crow, W.; van Den Berg, M.; Huffman, G.; Pellarin, T. Correcting rainfall using satellite-based surface soil moisture retrievals: The Soil Moisture Analysis Rainfall Tool (SMART). Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Román-Cascón, C.; Pellarin, T.; Gibon, F.; Brocca, L.; Cosme, E.; Crow, W.; Fernández-Prieto, D.; Kerr, Y.H.; Massari, C. Correcting satellite-based precipitation products through SMOS soil moisture data assimilation in two land-surface models of different complexity: API and SURFEX. Remote Sens. Environ. 2017, 200, 295–310. [Google Scholar] [CrossRef]
- Massari, C.; Brocca, L.; Moramarco, T.; Tramblay, Y.; Lescot, J.F.D. Potential of soil moisture observations in flood modelling: Estimating initial conditions and correcting rainfall. Adv. Water Resour. 2014, 74, 44–53. [Google Scholar] [CrossRef]
- Massari, C.; Camici, S.; Ciabatta, L.; Brocca, L. Exploiting Satellite-Based Surface Soil Moisture for Flood Forecasting in the Mediterranean Area: State Update Versus Rainfall Correction. Remote Sens. 2018, 10, 292. [Google Scholar] [CrossRef]
- Loew, A.; Stacke, T.; Dorigo, W.; De Jeu, R.; Hagemann, S. Potential and limitations of multidecadal satellite soil moisture observations for selected climate model evaluation studies. Hydrol. Earth Syst. Sci. 2013, 17, 3523–3542. [Google Scholar] [CrossRef] [Green Version]
- Polcher, J.; Piles, M.; Gelati, E.; Barella-Ortiz, A.; Tello, M. Comparing surface-soil moisture from the SMOS mission and the ORCHIDEE land-surface model over the Iberian Peninsula. Remote Sens. Environ. 2016, 174, 69–81. [Google Scholar] [CrossRef]
- Kidd, R.; Haas, E. ESA Climate Change Initiative Phase II Soil Moisture—USER GUIDE; EODC: Vienna, Austria, 2015; p. 56. [Google Scholar]
- Boening, C.; Willis, J.K.; Landerer, F.W.; Nerem, R.S.; Fasullo, J. The 2011 La Niña: So strong, the oceans fell. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Wilks, D. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 1995; pp. 51–54. [Google Scholar]
- McColl, K.A.; Alemohammad, S.H.; Akbar, R.; Konings, A.G.; Yueh, S.; Entekhabi, D. The global distribution and dynamics of surface soil moisture. Nat. Geosci. 2017, 10, 100. [Google Scholar] [CrossRef]
- Koster, R.D.; Milly, P. The interplay between transpiration and runoff formulations in land surface schemes used with atmospheric models. J. Clim. 1997, 10, 1578–1591. [Google Scholar] [CrossRef]
- Dee, D.P.; Da Silva, A.M. Data assimilation in the presence of forecast bias. Q. J. R. Meteorol. Soc. 1998, 124, 269–295. [Google Scholar] [CrossRef]
- Nearing, G.S.; Gupta, H.V.; Crow, W.T.; Gong, W. An approach to quantifying the efficiency of a Bayesian filter. Water Resour. Res. 2013, 49, 2164–2173. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Peters-Lidard, C.; Santanello, J.; Reichle, R.; Draper, C.; Koster, R.; Nearing, G.; Jasinski, M. Evaluating the utility of satellite soil moisture retrievals over irrigated areas and the ability of land data assimilation methods to correct for unmodeled processes. Hydrol. Earth Syst. Sci. 2015, 19, 4463–4478. [Google Scholar] [CrossRef] [Green Version]
- Massari, C.; Brocca, L.; Tarpanelli, A.; Moramarco, T. Data Assimilation of Satellite Soil Moisture into Rainfall-Runoff Modelling: A Complex Recipe? Remote Sens. 2015, 7, 11403–11433. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Crow, W.T.; Su, C.H.; Robertson, D.R. Dual assimilation of satellite soil moisture to improve streamflow prediction in data-scarce catchments. Water Resour. Res. 2016, 52, 5357–5375. [Google Scholar] [CrossRef]
- Ghannam, K.; Nakai, T.; Paschalis, A.; Oishi, C.A.; Kotani, A.; Igarashi, Y.; Kumagai, T.; Katul, G.G. Persistence and memory timescales in root-zone soil moisture dynamics. Water Resour. Res. 2016, 52, 1427–1445. [Google Scholar] [CrossRef] [Green Version]
- Best, M.; Pryor, M.; Clark, D.; Rooney, G.; Essery, R.; Ménard, C.; Edwards, J.; Hendry, M.; Porson, A.; Gedney, N.; et al. The Joint UK Land Environment Simulator (JULES), model description—Part 1: Energy and water fluxes. Geosci. Model Dev. 2011, 4, 677–699. [Google Scholar] [CrossRef]
- Clark, D.; Mercado, L.; Sitch, S.; Jones, C.; Gedney, N.; Best, M.; Pryor, M.; Rooney, G.; Essery, R.; Blyth, E.; et al. The Joint UK Land Environment Simulator (JULES), model description—Part 2: Carbon fluxes and vegetation dynamics. Geosci. Model Dev. 2011, 4, 701–722. [Google Scholar] [CrossRef] [Green Version]
- Raddatz, T.; Reick, C.; Knorr, W.; Kattge, J.; Roeckner, E.; Schnur, R.; Schnitzler, K.G.; Wetzel, P.; Jungclaus, J. Will the tropical land biosphere dominate the climate–carbon cycle feedback during the twenty-first century? Clim. Dyn. 2007, 29, 565–574. [Google Scholar] [CrossRef]
- Scholze, M.; Kaminski, T.; Knorr, W.; Blessing, S.; Vossbeck, M.; Grant, J.; Scipal, K. Simultaneous assimilation of SMOS soil moisture and atmospheric CO2 in-situ observations to constrain the global terrestrial carbon cycle. Remote Sens. Environ. 2016, 180, 334–345. [Google Scholar] [CrossRef]
- Peylin, P.; Bacour, C.; MacBean, N.; Leonard, S.; Rayner, P.; Kuppel, S.; Koffi, E.; Kane, A.; Maignan, F.; Chevallier, F.; et al. A new stepwise carbon cycle data assimilation system using multiple data streams to constrain the simulated land surface carbon cycle. Geosci. Model Dev. 2016, 9, 3321. [Google Scholar] [CrossRef]










| Layer | Layer Thickness (m) | Integrated Depth (m) |
|---|---|---|
| 1 | 0.001 | 0.001 |
| 2 | 0.003 | 0.004 |
| 3 | 0.006 | 0.010 |
| 4 | 0.012 | 0.022 |
| 5 | 0.023 | 0.045 |
| 6 | 0.047 | 0.092 |
| 7 | 0.092 | 0.186 |
| 8 | 0.188 | 0.374 |
| 9 | 0.375 | 0.750 |
| 10 | 0.750 | 1.500 |
| 11 | 0.500 | 2.000 |
| Simulation | Climate Forcing | Land Cover | Soil Resistance |
|---|---|---|---|
| ORC_REF | CERASAT | LC6 | Y |
| ORC_CRU | CRUNCEP | LC6 | Y |
| ORC_LC5 | CERASAT | LC5 | Y |
| ORC_NoRs | CERASAT | LC6 | N |
| Data | Covarying Pattern | Explained Covariance | Explained Variance of SM Patterns | Correlations between Covarying Patterns of SM and P | ||
|---|---|---|---|---|---|---|
| by Precip. (Heterogeneous) | by SM Itself (Homogeneous) | Spatial | Temporal (Expansion Coeff.) | |||
| Australia | ||||||
| ESA-CC1 | PC1 | 85.2 | 12.73 | 21.71 | 0.92 | 0.76 |
| PC2 | 5.15 | 4.05 | 23.6 | 0.84 | 0.42 | |
| PC3 | 4.55 | 2.34 | 9.87 | 0.92 | 0.5 | |
| 94.9 | 19.12 | 55.18 | 0.89 | 0.56 | ||
| ORC_REF | PC1 | 81.97 | 20.61 | 29.46 | 0.90 | 0.83 |
| PC2 | 6.77 | 4.01 | 13.82 | 0.95 | 0.56 | |
| PC3 | 5.03 | 5.50 | 17.97 | 0.92 | 0.57 | |
| 93.77 | 30.12 | 61.25 | 0.92 | 0.65 | ||
| ORC_CRU | PC1 | 86.69 | 19.91 | 29.76 | 0.87 | 0.80 |
| PC2 | 5.08 | 3.01 | 15.37 | 0.92 | 0.46 | |
| PC3 | 3.50 | 3.50 | 14.27 | 0.86 | 0.52 | |
| 95.27 | 26.42 | 59.40 | 0.88 | 0.59 | ||
| The Iberian Peninsula | ||||||
| ESA-CC1 | PC1 | 96.78 | 15.89 | 75.81 | 0.56 | 0.46 |
| PC2 | 1.65 | 1.39 | 8.89 | 0.89 | 0.4 | |
| PC3 | 1.04 | 0.82 | 5.25 | 0.87 | 0.41 | |
| 99.47 | 18.1 | 89.95 | 0.77 | 0.42 | ||
| ORC_REF | PC1 | 95.12 | 23.68 | 81.96 | 0.52 | 0.54 |
| PC2 | 2.52 | 3.11 | 12.4 | 0.95 | 0.52 | |
| PC3 | 1.79 | 2.29 | 8.36 | 0.96 | 0.54 | |
| 99.43 | 29.08 | 102.72 | 0.81 | 0.53 | ||
| ORC_CRU | PC1 | 95.71 | 18.99 | 80.24 | 0.68 | 0.49 |
| PC2 | 2.12 | 1.71 | 11.92 | 0.89 | 0.42 | |
| PC3 | 01.58 | 1.51 | 10.15 | 0.94 | 0.44 | |
| 99.41 | 22.21 | 102.31 | 0.84 | 0.45 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raoult, N.; Delorme, B.; Ottlé, C.; Peylin, P.; Bastrikov, V.; Maugis, P.; Polcher, J. Confronting Soil Moisture Dynamics from the ORCHIDEE Land Surface Model With the ESA-CCI Product: Perspectives for Data Assimilation. Remote Sens. 2018, 10, 1786. https://doi.org/10.3390/rs10111786
Raoult N, Delorme B, Ottlé C, Peylin P, Bastrikov V, Maugis P, Polcher J. Confronting Soil Moisture Dynamics from the ORCHIDEE Land Surface Model With the ESA-CCI Product: Perspectives for Data Assimilation. Remote Sensing. 2018; 10(11):1786. https://doi.org/10.3390/rs10111786
Chicago/Turabian StyleRaoult, Nina, Bertrand Delorme, Catherine Ottlé, Philippe Peylin, Vladislav Bastrikov, Pascal Maugis, and Jan Polcher. 2018. "Confronting Soil Moisture Dynamics from the ORCHIDEE Land Surface Model With the ESA-CCI Product: Perspectives for Data Assimilation" Remote Sensing 10, no. 11: 1786. https://doi.org/10.3390/rs10111786
APA StyleRaoult, N., Delorme, B., Ottlé, C., Peylin, P., Bastrikov, V., Maugis, P., & Polcher, J. (2018). Confronting Soil Moisture Dynamics from the ORCHIDEE Land Surface Model With the ESA-CCI Product: Perspectives for Data Assimilation. Remote Sensing, 10(11), 1786. https://doi.org/10.3390/rs10111786