Compressive Sensing for Ground Based Synthetic Aperture Radar
Abstract
:1. Introduction
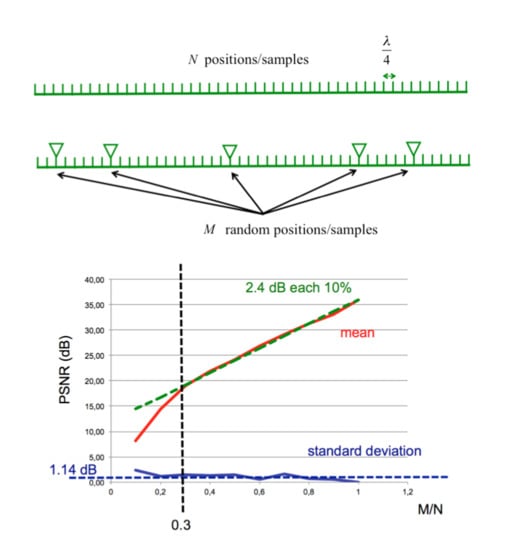
2. Materials and Methods
3. Results
3.1. Simulations
3.2. Experimental Test Site “Campus”
3.3. A Seven-Storey Building
3.4. An Open-Pit Copper Mine
3.5. A Glacier
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Luzi, G.; Pieraccini, M.; Mecatti, D.; Noferini, L.; Macaluso, G.; Galgaro, A.; Atzeni, C. Advances in groundbased microwave interferometry for landslide survey: A case study. Int. J. Remote Sens. 2006, 27, 2331–2350. [Google Scholar] [CrossRef]
- Noferini, L.; Pieraccini, T.T.M.; Mecatti, D.; Macaluso, G.; Luzi, G.; Atzeni, C. Analysis of ground-based SAR data with diverse temporal baselines. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1614–1623. [Google Scholar] [CrossRef]
- Noferini, L.; Mecatti, D.; Macaluso, G.; Pieraccini, M.; Atzeni, C. Monitoring of Belvedere Glacier using a wide angle GB-SAR interferometer. J. Appl. Geophys. 2009, 68, 289–293. [Google Scholar] [CrossRef]
- Liu, B.; Ge, D.; Li, M.; Zhang, L.; Wang, Y.; Zhang, X. Using GB-SAR technique to monitor displacement of open pit slope. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5986–5989. [Google Scholar]
- Pieraccini, M.; Tarchi, D.; Rudolf, H.; Leva, D.; Luzi, G.; Bartoli, G.; Atzeni, C. Structural static testing by interferometric synthetic radar. NDT E Int. 2000, 33, 565–570. [Google Scholar] [CrossRef]
- Jenkins, W.; Rosenblad, B.; Gomez, F.; Le-garsky, J.; Loehr, E. Deformation measurements of earth dams using a ground based inter-ferometric radar. In Proceedings of the 2012 ASDSO Annual Conference on Dam Safety, Denver, CO, USA, 16–20 September 2012. [Google Scholar]
- Candès, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Massa, A.; Rocca, P.; Oliveri, G. Compressive sensing in electromagnetics-a review. IEEE Antennas Propag. Mag. 2015, 57, 224–238. [Google Scholar] [CrossRef]
- Hadi, M.A.; Alshebeili, S.; Jamil, K.; El-Samie, F.E.A. Compressive sensing applied to radar systems: An overview. Signal Image Video Process. 2015, 9, 25–39. [Google Scholar] [CrossRef]
- Huang, Q.; Qu, L.; Wu, B.; Fang, G. UWB through-wall imaging based on compressive sensing. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1408–1415. [Google Scholar] [CrossRef]
- Karlina, R.; Sato, M. Compressive sensing applied to imaging by ground-based polarimetric SAR. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2011), Vancouver, BC, Canada, 24–29 July 2011. [Google Scholar]
- Zonno, M. GBSAR data focusing based on compressive sensing. In Proceedings of the 10th European Conference on Synthetic Aperture Radar EUSAR 2014, Berlin, Germany, 3–5 June 2014. [Google Scholar]
- Yiğit, E. Compressed sensing for millimeter-wave ground based SAR/ISAR imaging. J. Infrared Millim. Terahertz Waves 2014, 35, 932–948. [Google Scholar] [CrossRef]
- Giordano, R.; Guccione, P.; Cifarelli, G.; Mascolo, L.; Nico, G. Focusing SAR images by compressive sensing: Study of interferometric properties. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 5352–5355. [Google Scholar]
- Feng, W.; Yi, L.; Sato, M. Near range radar imaging based on block sparsity and cross-correlation fusion algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2079–2089. [Google Scholar] [CrossRef]
- Tarchi, D.; Oliveri, F.; Sammartino, P.F. MIMO radar and ground-based SAR imaging systems: Equivalent approaches for remote sensing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 425–435. [Google Scholar] [CrossRef]
- Hu, C.; Wang, J.; Tian, W.; Zeng, T.; Wang, R. Design and Imaging of Ground-Based Multiple-Input Multiple-Output Synthetic Aperture Radar (MIMO SAR) with Non-Collinear Arrays. Sensors 2017, 17, 598. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Carin, L. Exploiting structure in wavelet-based Bayesian compressive sensing. IEEE Trans. Signal Process. 2009, 57, 3488–3497. [Google Scholar]
- Chui, C.K. An Introduction to Wavelets; Academic Press: San Diego, CA, USA, 1992. [Google Scholar]
- Walker, J.S. A Primer on Wavelets and Their Scientific Applications; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Wickerhauser, M.V. Adapted Wavelet Analysis from Theory to Software; IEEE Press: Piscataway, NJ, USA, 1994. [Google Scholar]
- Yang, A.Y.; Sastry, S.S.; Ganesh, A.; Ma, Y. Fast ℓ1-minimization algorithms and an application in robust face recognition: A review. In Proceedings of the 17th IEEE International Conference on Image Processing (ICIP), Hong Kong, China, 26–29 September 2010; pp. 1849–1852. [Google Scholar]
- Baraniuk, R.G. Compressive sensing [lecture notes]. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Pieraccini, M.; Miccinesi, L. ArcSAR: Theory, simulations, and experimental verification. IEEE Trans. Microw. Theory Tech. 2017, 65, 293–301. [Google Scholar] [CrossRef]
- Salomon, D. Data Compression: The Complete Reference; Springer: New York, NY, USA, 2004. [Google Scholar]
- Pieraccini, M.; Noferini, L.; Mecatti, D.; Macaluso, G.; Luzi, G.; Atzeni, C. Digital elevation models by a GBSAR interferometer for monitoring glaciers: The case study of Belvedere Glacier. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2008, Boston, MA, USA, 7–11 July 2008; Volume 4, p. IV-1061. [Google Scholar]
- Pieraccini, M.; Luzi, G.; Mecatti, D.; Noferini, L.; Atzeni, C. Ground-based SAR for short and long term monitoring of unstable slopes. In Proceedings of the 3rd European Radar Conference, EuRAD 2006, Manchester, UK, 13–15 September 2006; pp. 92–95. [Google Scholar]

























| 50% | 33% | |||||
|---|---|---|---|---|---|---|
| L1 (dB) | L2 (dB) | OMP (dB) | L1 (dB) | L2 (dB) | OMP (dB) | |
| Dct | 22.92 | 22.89 | 22.29 | 18.77 | 19.02 | 19.62 |
| Fft | 22.61 | 22.73 | 21.89 | 17.00 | 17.16 | 17.45 |
| Haar | 24.83 | 24.83 | 26.01 | 18.30 | 18.30 | 20.03 |
| Db2 | 24.32 | 24.29 | 24.32 | 18.14 | 18.13 | 18.13 |
| Db3 | 24.32 | 24.33 | 24.36 | 17.68 | 17.66 | 18.01 |
| Db4 | 23.97 | 23.97 | 23.67 | 18.22 | 18.23 | 17.98 |
| Db5 | 23.71 | 23.73 | 23.10 | 17.49 | 17.48 | 17.35 |
| Db6 | 23.87 | 23.90 | 22.74 | 17.76 | 17.77 | 17.98 |
| Db7 | 23.24 | 23.25 | 22.60 | 17.41 | 17.45 | 16.11 |
| Db8 | 23.24 | 23.23 | 22.48 | 17.71 | 17.70 | 17.82 |
| Db9 | 23.26 | 23.27 | 21.46 | 17.71 | 17.72 | 17.82 |
| Db10 | 23.04 | 23.07 | 23.48 | 17.74 | 17.74 | 18.52 |
| Bior1.3 | 24.65 | 24.64 | 25.00 | 18.16 | 18.16 | 19.51 |
| Bior2.2 | 24.45 | 24.45 | 23.53 | 17.00 | 16.99 | 16.96 |
| Bior2.6 | 24.22 | 24.21 | 23.37 | 17.65 | 17.65 | 17.37 |
| Bior3.1 | 23.51 | 23.51 | 22.66 | 17.39 | 17.39 | 15.87 |
| Bior3.5 | 24.29 | 24.28 | 23.50 | 17.99 | 17.99 | 17.21 |
| Bior3.9 | 24.00 | 24.04 | 23.67 | 17.60 | 17.60 | 17.67 |
| Bior5.5 | 23.97 | 23.98 | 23.62 | 18.04 | 18.07 | 18.23 |
| Coif1 | 24.04 | 24.09 | 23.52 | 17.71 | 17.72 | 17.25 |
| Coif2 | 24.20 | 24.21 | 24.04 | 16.84 | 16.84 | 17.26 |
| Coif3 | 23.72 | 23.72 | 23.27 | 17.39 | 17.39 | 17.36 |
| Coif4 | 23.47 | 23.47 | 22.74 | 17.49 | 17.51 | 17.52 |
| Coif5 | 23.28 | 23.18 | 22.79 | 17.05 | 17.04 | 16.90 |
| Sym2 | 24.32 | 24.29 | 24.32 | 18.14 | 18.13 | 18.13 |
| Sym3 | 24.32 | 24.33 | 24.36 | 17.68 | 17.66 | 18.01 |
| Sym4 | 24.42 | 24.44 | 24.08 | 17.29 | 17.28 | 17.04 |
| Sym5 | 23.77 | 23.77 | 23.62 | 17.63 | 17.64 | 17.54 |
| Sym6 | 24.24 | 24.15 | 23.78 | 17.64 | 17.64 | 16.94 |
| Sym7 | 24.26 | 24.27 | 24.18 | 18.02 | 18.03 | 17.68 |
| Sym8 | 24.10 | 24.11 | 23.53 | 17.94 | 17.94 | 17.04 |
| Legall5.3 | 24.17 | 24.17 | 24.49 | 18.31 | 18.30 | 18.51 |
| Dmey | 23.60 | 23.60 | 23.56 | 17.93 | 17.94 | 17.96 |
| 50% | 33% | |||||
|---|---|---|---|---|---|---|
| L1 (dB) | L2 (dB) | OMP (dB) | L1 (dB) | L2 (dB) | OMP (dB) | |
| Dct | 16.47 | 16.59 | 8.16 | 11.04 | 10.85 | 5.93 |
| Fft | 15.62 | 15.30 | 10.72 | 9.33 | 9.98 | 1.80 |
| Haar | 22.73 | 22.73 | 21.59 | 19.00 | 19.00 | 18.42 |
| Db2 | 21.50 | 21.52 | 22.78 | 18.33 | 18.32 | 18.85 |
| Db3 | 21.60 | 21.62 | 22.72 | 18.13 | 18.13 | 18.86 |
| Db4 | 21.55 | 21.58 | 20.99 | 17.84 | 17.83 | 17.85 |
| Db5 | 21.01 | 21.02 | 21.60 | 17.91 | 17.93 | 19.12 |
| Db6 | 20.09 | 20.90 | 21.39 | 17.91 | 17.91 | 18.98 |
| Db7 | 20.48 | 20.52 | 20.67 | 17.79 | 17.75 | 18.49 |
| Db8 | 19.16 | 19.17 | 19.15 | 14.70 | 14.70 | 16.17 |
| Db9 | 19.11 | 19.14 | 17.81 | 17.05 | 17.04 | 16.32 |
| Db10 | 19.82 | 19.83 | 19.27 | 17.03 | 17.05 | 17.69 |
| Bior1.3 | 22.26 | 22.27 | 21.49 | 18.78 | 18.79 | 17.58 |
| Bior2.2 | 21.91 | 21.92 | 22.42 | 18.13 | 18.13 | 18.27 |
| Bior2.6 | 21.31 | 21.32 | 22.36 | 17.67 | 17.68 | 18.58 |
| Bior3.1 | 21.27 | 21.31 | 20.56 | 20.10 | 20.10 | 19.16 |
| Bior3.5 | 20.12 | 20.12 | 19.63 | 17.49 | 17.54 | 17.33 |
| Bior3.9 | 20.79 | 20.80 | 19.41 | 17.77 | 17.80 | 16.45 |
| Bior5.5 | 22.13 | 22.14 | 22.76 | 17.80 | 17.83 | 19.11 |
| Coif1 | 21.76 | 21.76 | 21.74 | 18.33 | 18.34 | 17.96 |
| Coif2 | 21.98 | 21.96 | 21.90 | 17.85 | 17.85 | 17.86 |
| Coif3 | 21.77 | 21.77 | 21.77 | 18.29 | 18.30 | 18.74 |
| Coif4 | 20.21 | 20.21 | 21.88 | 17.87 | 17.89 | 18.89 |
| Coif5 | 21.38 | 21.38 | 21.67 | 18.00 | 18.00 | 18.66 |
| Sym2 | 21.50 | 21.52 | 22.78 | 18.33 | 18.32 | 18.84 |
| Sym3 | 21.61 | 21.61 | 22.72 | 18.13 | 18.13 | 18.86 |
| Sym4 | 21.45 | 21.44 | 21.18 | 18.15 | 18.25 | 18.00 |
| Sym5 | 21.36 | 21.38 | 20.18 | 17.84 | 17.81 | 18.76 |
| Sym6 | 21.13 | 21.12 | 20.96 | 17.47 | 17.44 | 18.04 |
| Sym7 | 21.79 | 21.80 | 21.52 | 17.22 | 17.22 | 18.34 |
| Sym8 | 21.47 | 21.47 | 20.04 | 16.90 | 16.93 | 17.86 |
| Legall5.3 | 22.03 | 22.04 | 22.64 | 18.06 | 18.06 | 18.47 |
| Dmey | 20.55 | 20.59 | 19.16 | 17.46 | 17.46 | 16.95 |
| 50% | 33% | |||||
|---|---|---|---|---|---|---|
| L1 (dB) | L2 (dB) | OMP (dB) | L1 (dB) | L2 (dB) | OMP (dB) | |
| Dct | 17.54 | 18.23 | 17.36 | 15.84 | 16.31 | 15.90 |
| Fft | 17.41 | 17.25 | 15.26 | 11.69 | 12.44 | 10.05 |
| Haar | 29.39 | 29.39 | 29.95 | 25.81 | 25.81 | 29.44 |
| Db2 | 28.29 | 28.30 | 28.25 | 26.29 | 26.30 | 27.69 |
| Db3 | 25.34 | 25.37 | 27.85 | 23.94 | 23.94 | 26.22 |
| Db4 | 24.54 | 24.53 | 23.14 | 22.48 | 22.48 | 22.94 |
| Db5 | 25.69 | 25.70 | 23.68 | 21.38 | 21.37 | 22.74 |
| Db6 | 25.24 | 25.24 | 26.30 | 22.26 | 22.26 | 22.49 |
| Db7 | 25.88 | 25.89 | 24.14 | 21.48 | 21.49 | 23.01 |
| Db8 | 24.08 | 24.10 | 21.70 | 20.82 | 20.82 | 19.29 |
| Db9 | 24.04 | 24.05 | 19.98 | 21.28 | 21.29 | 16.25 |
| Db10 | 23.68 | 23.68 | 18.82 | 22.25 | 22.26 | 18.27 |
| Bior1.3 | 28.79 | 28.79 | 27.45 | 25.42 | 25.42 | 27.47 |
| Bior2.2 | 27.60 | 27.59 | 26.63 | 22.73 | 22.72 | 18.68 |
| Bior2.6 | 26.41 | 26.41 | 26.28 | 22.62 | 22.60 | 19.09 |
| Bior3.1 | 26.43 | 26.44 | 22.56 | 24.38 | 24.38 | 14.96 |
| Bior3.5 | 25.54 | 25.55 | 21.41 | 22.85 | 22.86 | 17.30 |
| Bior3.9 | 25.18 | 25.19 | 20.49 | 22.70 | 23.17 | 18.03 |
| Bior5.5 | 25.24 | 25.24 | 27.26 | 23.33 | 23.35 | 26.33 |
| Coif1 | 27.13 | 27.14 | 26.58 | 21.32 | 21.33 | 20.95 |
| Coif2 | 24.83 | 24.84 | 24.01 | 20.74 | 20.75 | 21.29 |
| Coif3 | 25.05 | 25.06 | 23.73 | 22.37 | 22.37 | 21.18 |
| Coif4 | 26.10 | 26.09 | 25.56 | 22.97 | 22.97 | 22.85 |
| Coif5 | 26.05 | 26.05 | 25.94 | 22.80 | 22.80 | 25.93 |
| Sym2 | 28.29 | 28.30 | 28.25 | 26.29 | 26.30 | 27.69 |
| Sym3 | 25.34 | 25.35 | 27.85 | 23.94 | 23.94 | 26.22 |
| Sym4 | 25.47 | 25.46 | 25.63 | 21.94 | 21.94 | 19.47 |
| Sym5 | 27.62 | 27.63 | 25.54 | 23.01 | 23.06 | 24.35 |
| Sym6 | 25.53 | 25.54 | 25.08 | 22.45 | 22.45 | 18.56 |
| Sym7 | 24.95 | 24.96 | 26.10 | 24.48 | 24.48 | 25.98 |
| Sym8 | 25.50 | 25.54 | 24.26 | 22.18 | 22.21 | 18.73 |
| Legall5.3 | 28.78 | 28.78 | 29.39 | 26.78 | 26.78 | 27.58 |
| Dmey | 25.15 | 25.16 | 21.72 | 22.31 | 22.31 | 18.04 |
| 50% | 33% | |||||
|---|---|---|---|---|---|---|
| L1 (dB) | L2 (dB) | OMP (dB) | L1 (dB) | L2 (dB) | OMP (dB) | |
| Dct | −2.26 | −3.50 | −2.77 | 1.34 | 1.39 | 0.21 |
| Fft | −1.67 | 1.85 | −0.92 | −5.09 | −4.93 | −4.06 |
| Haar | 20.53 | 20.53 | 21.16 | 15.01 | 15.02 | 16.52 |
| Db2 | 13.53 | 13.53 | 19.27 | 8.21 | 8.26 | 14.09 |
| Db3 | 9.54 | 9.54 | 18.83 | 5.64 | 5.75 | 14.02 |
| Db4 | 4.05 | 4.10 | 13.05 | 8.75 | 8.75 | 8.56 |
| Db5 | 5.56 | 5.69 | 11.14 | 7.17 | 7.19 | 10.53 |
| Db6 | 2.89 | 2.87 | 17.51 | 3.79 | 3.87 | 11.77 |
| Db7 | 11.26 | 11.24 | 10.67 | 8.68 | 8.67 | 5.58 |
| Db8 | 2.62 | 2.64 | 8.83 | 1.78 | 1.77 | 0.92 |
| Db9 | 6.69 | 6.74 | 10.25 | 5.53 | 5.52 | −3.23 |
| Db10 | 2.32 | 2.33 | 3.29 | −2.96 | −2.90 | 2.16 |
| Bior1.3 | 13.96 | 13.95 | 10.27 | 11.45 | 11.41 | 8.57 |
| Bior2.2 | 14.37 | 14.39 | 19.17 | 9.93 | 9.92 | 13.99 |
| Bior2.6 | 9.84 | 9.86 | 18.15 | 6.91 | 7.01 | 13.03 |
| Bior3.1 | 6.65 | 6.64 | 5.16 | 7.50 | 7.46 | 8.46 |
| Bior3.5 | 4.81 | 4.81 | 2.93 | 7.21 | 7.21 | 10.65 |
| Bior3.9 | 3.31 | 3.27 | -3.01 | 6.08 | 6.53 | 7.56 |
| Bior5.5 | 10.55 | 10.52 | 14.62 | 4.11 | 4.09 | 14.02 |
| Coif1 | 10.98 | 11.11 | 19.72 | 10.58 | 10.61 | 14.27 |
| Coif2 | 12.17 | 12.16 | 19.66 | 7.98 | 7.99 | 14.55 |
| Coif3 | 9.48 | 9.48 | 18.72 | 6.56 | 6.56 | 10.16 |
| Coif4 | 11.65 | 11.65 | 14.46 | 5.76 | 5.75 | 11.57 |
| Coif5 | 5.87 | 5.88 | 11.36 | 9.49 | 9.49 | 3.42 |
| Sym2 | 13.53 | 13.53 | 19.28 | 8.21 | 8.26 | 14.09 |
| Sym3 | 9.54 | 9.54 | 18.83 | 5.64 | 5.75 | 14.02 |
| Sym4 | 11.14 | 11.19 | 17.39 | 10.10 | 10.10 | 14.03 |
| Sym5 | 9.52 | 9.51 | 9.78 | 4.83 | 4.51 | 3.63 |
| Sym6 | 12.48 | 12.49 | 12.94 | 7.37 | 7.37 | 7.37 |
| Sym7 | 9.35 | 9.37 | 16.86 | 2.44 | 2.45 | 11.40 |
| Sym8 | 13.64 | 13.59 | 12.17 | 7.00 | 7.00 | 11.34 |
| Legall5.3 | 11.76 | 11.79 | 15.75 | 9.43 | 9.40 | 14.62 |
| Dmey | 6.83 | 6.84 | 10.72 | 5.60 | 5.61 | 11.78 |
| Campus | Building | Mine | Glacier | |
|---|---|---|---|---|
| f1 (GHz) | 9.915 | 9.915 | 17.1 | 5.97 |
| f2 (GHz) | 10.075 | 10.075 | 17.3 | 5.99 |
| Nf | 801 | 801 | 5333 | 801 |
| L (m) | 1 | 1.8 | 1.275 | 1.71 |
| N | 100 | 180 | 256 | 141 |
| PSNR max 50% (dB) | 26.01 | 22.78 | 29.95 | 21.16 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pieraccini, M.; Rojhani, N.; Miccinesi, L. Compressive Sensing for Ground Based Synthetic Aperture Radar. Remote Sens. 2018, 10, 1960. https://doi.org/10.3390/rs10121960
Pieraccini M, Rojhani N, Miccinesi L. Compressive Sensing for Ground Based Synthetic Aperture Radar. Remote Sensing. 2018; 10(12):1960. https://doi.org/10.3390/rs10121960
Chicago/Turabian StylePieraccini, Massimiliano, Neda Rojhani, and Lapo Miccinesi. 2018. "Compressive Sensing for Ground Based Synthetic Aperture Radar" Remote Sensing 10, no. 12: 1960. https://doi.org/10.3390/rs10121960
APA StylePieraccini, M., Rojhani, N., & Miccinesi, L. (2018). Compressive Sensing for Ground Based Synthetic Aperture Radar. Remote Sensing, 10(12), 1960. https://doi.org/10.3390/rs10121960