Spectral Mixture Analysis as a Unified Framework for the Remote Sensing of Evapotranspiration
Abstract
:1. Introduction
1.1. ET Model Overview
1.1.1. Models Relying on V vs T
1.1.2. Models Relying on α vs T
1.2. Spectral Mixture Analysis
2. Materials and Methods
2.1. Data
2.2. Spectral Mixture Analysis
2.3. ET Estimation Using the Triangle Method
2.4. Study Area
3. Results
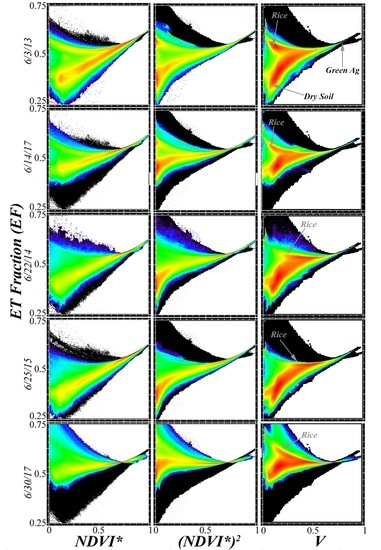
3.1. Vegetation Metric Comparison
3.2. Dark Fraction and Albedo
3.3. Substrate Fraction, Temperature, and ET
4. Discussion
4.1. Application Examples
4.2. Evaluation
4.3. ET Partitioning
4.4. Thermal EM Selection
4.5. Clustering in Fraction vs ET Parameter Space
4.6. The SVD Approach as a Unifying Framework
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Miralles, D.G.; van den Berg, M.J.; Gash, J.H.; Parinussa, R.M.; de Jeu, R.A.M.; Beck, H.E.; Holmes, T.R.H.; Jiménez, C.; Verhoest, N.E.C.; Dorigo, W.A.; et al. El Niño–La Niña cycle and recent trends in continental evaporation. Nat. Clim. Chang. 2013, 4, 122–126. [Google Scholar] [CrossRef]
- Miralles, D.G.; Van Den Berg, M.J.; Teuling, A.J.; De Jeu, R.A.M. Soil moisture-temperature coupling: A multiscale observational analysis. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.C.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Peña-Arancibia, J.L.; McVicar, T.R.; Chiew, F.H.S.; Vaze, J.; Liu, C.; Lu, X.; Zheng, H.; Wang, Y.; Liu, Y.Y.; et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 2016, 6, 19124. [Google Scholar] [PubMed] [Green Version]
- Jackson, R.D.; Reginato, R.J.; Idso, S.B. Wheat canopy temperature: A practical tool for evaluating water requirements. Water Resour. Res. 1977, 13, 651–656. [Google Scholar] [CrossRef]
- Jackson, R.D.; Idso, S.B.; Reginato, R.J.; Pinter, P.J., Jr. Canopy temperature as a crop water stress indicator. Water Resour. Res. 1981, 17, 1133–1138. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D.; Reginato, R.J. Remote-Sensing of Crop Yields. Science 1977, 196, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R. A Landsat-based energy balance and evapotranspiration model in Western US water rights regulation and planning. Irrig. Drain. Syst. 2005, 19, 251–268. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL Model with Remotely Sensed Data to Improve Water-Resources Management under Actual Field Conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
- Farahani, H.; Howell, T.A.; Shuttleworth, W.J.; Bausch, W.C. Evapotranspiration: Progress in Measurement and Modeling in Agriculture. Trans. ASABE 2007, 50, 1627–1638. [Google Scholar] [CrossRef] [Green Version]
- Fisher, J.B.; Whittaker, R.J.; Malhi, Y. ET come home: Potential evapotranspiration in geographical ecology. Glob. Ecol. Biogeogr. 2011, 20, 1–18. [Google Scholar] [CrossRef]
- Gaston, K.J. Global patterns in biodiversity. Nature 2000, 405, 220–227. [Google Scholar] [CrossRef] [PubMed]
- Shafroth, P.B.; Brown, C.A.; Merritt, D.M. Saltcedar and Russian olive control demonstration act science assessment. In Scientific Investigations Report 2009-5247; U.S. Geologic Survey: Reston, VA, USA, 2010. [Google Scholar]
- Anderson, M.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC) Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Carlson, T.N.; Boland, F.E. Analysis of urban-rural canopy using a surface heat flux/temperature model. J. Appl. Meteorol. 1978, 17, 998–1013. [Google Scholar] [CrossRef]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Wang, L.; Good, S.P.; Caylor, K.K. Global synthesis of vegetation control on evapotranspiration partitioning. Geophys. Res. Lett. 2014, 41, 6753–6757. [Google Scholar] [CrossRef] [Green Version]
- Menenti, M.; Bastiaanssen, W.; Van Eick, D.; El Karim, M.A.A. Linear relationships between surface reflectance and temperature and their application to map actual evaporation of groundwater. Adv. Space Res. 1989, 9, 165–176. [Google Scholar] [CrossRef]
- Ångström, A. The Albedo of Various Surfaces of Ground. Geogr. Ann. 1925, 7, 323–342. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D.; Reginato, R.J.; Kimball, B.A.; Nakayama, F.S. The dependence of bare soil albedo on soil water content. J. Appl. Meteorol. 1975, 14, 109–113. [Google Scholar] [CrossRef]
- Matthias, A.D.; Fimbres, A.; Sano, E.E.; Post, D.F.; Accioly, L.; Batchily, A.K.; Ferreira, L.G. Surface roughness effects on soil albedo. Soil Sci. Soc. Am. J. 2000, 64, 1035–1041. [Google Scholar] [CrossRef]
- Roerink, G.J.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth Part B Hydrol. Ocean. Atmos. 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Merlin, O.; Chirouze, J.; Olioso, A.; Jarlan, L.; Chehbouni, G.; Boulet, G. An image-based four-source surface energy balance model to estimate crop evapotranspiration from solar reflectance/thermal emission data (SEB-4S). Agric. For. Meteorol. 2014, 184, 188–203. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.; Islam, S. A methodology for estimation of surface evapotranspiration over large areas using remote sensing observations. Geophys. Res. Lett. 1999, 26, 2773–2776. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index-radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Elmore, A.J.; Mustard, J.F.; Manning, S.J.; Lobell, D.B. Quantifying vegetation change in semiarid environments: Precision and accuracy of spectral mixture analysis and the normalized difference vegetation index. Remote Sens. Environ. 2000, 73, 87–102. [Google Scholar] [CrossRef]
- Price, J.C. Using spatial context in satellite data to infer regional scale evapotranspiration. IEEE Trans. Geosci. Remote Sens. 1990, 28, 940–948. [Google Scholar] [CrossRef] [Green Version]
- Small, C. Estimation of urban vegetation abundance by spectral mixture analysis. Int. J. Remote Sens. 2001, 22, 1305–1334. [Google Scholar] [CrossRef] [Green Version]
- Smith, M.O.; Ustin, S.L.; Adams, J.B.; Gillespie, A.R. Vegetation in deserts: I. A regional measure of abundance from multispectral images. Remote Sens. Environ. 1990, 31, 1–26. [Google Scholar] [CrossRef]
- Small, C.; Milesi, C. Multi-scale standardized spectral mixture models. Remote Sens. Environ. 2013, 136, 442–454. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, C.S. Relations between evaporation coefficients and vegetation indices studied by model simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar] [CrossRef]
- Carlson, T.N. An Overview of the “Triangle Method” for Estimating Surface Evapotranspiration and Soil Moisture from Satellite Imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Sun, H. A Two-Source Model for Estimating Evaporative Fraction (TMEF) Coupling Priestley-Taylor Formula and Two-Stage Trapezoid. Remote Sens. 2016, 8, 248. [Google Scholar] [CrossRef]
- Li, G.; Jing, Y.; Wu, Y.; Zhang, F.; Li, G.; Jing, Y.; Wu, Y.; Zhang, F. Improvement of Two Evapotranspiration Estimation Models Using a Linear Spectral Mixture Model over a Small Agricultural Watershed. Water 2018, 10, 474. [Google Scholar] [CrossRef]
- Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral mixture modeling: A new analysis of rock and soil types at the Viking Lander 1 site. J. Geophys. Res. Solid Earth 1986, 91, 8098–8112. [Google Scholar] [CrossRef]
- Gillespie, A.R.; Smith, M.O.; Adams, J.B.; Willis, S.C.; Fischer, A.F.; Sabol, D.E. Interpretation of residual images: Spectral mixture analysis of AVIRIS images, Owens Valley, California. In Annual JPL Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) Workshop; NASA Jet Propulsion Laboratory: Pasadena, CA, USA, 1990; Volume 2, pp. 54–90. [Google Scholar]
- Smith, M.O.; Johnson, P.E.; Adams, J.B. Quantitative determination of mineral types and abundances from reflectance spectra using principal components analysis. J. Geophys. Res. Solid Earth 1985, 90, C797–C804. [Google Scholar] [CrossRef]
- Baldocchi, D.; Krebs, T.; Leclerc, M.Y. “Wet/dry Daisyworld”: A conceptual tool for quantifying the spatial scaling of heterogeneous landscapes and its impact on the subgrid variability of energy fluxes. Tellus B Chem. Phys. Meteorol. 2005, 57, 175–188. [Google Scholar] [CrossRef]
- Brunsell, N.; Gillies, R. Length Scale Analysis of Surface Energy Fluxes Derived from Remote Sensing. J. Hydrometeorol. 2003, 4, 1212–1219. [Google Scholar] [CrossRef] [Green Version]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ. 2006, 105, 271–285. [Google Scholar] [CrossRef]
- Brunsell, N.; Anderson, M. Characterizing the multi–scale spatial structure of remotely sensed evapotranspiration with information theory. Biogeosciences 2011, 8, 2269–2280. [Google Scholar] [CrossRef] [Green Version]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Walker, J.P. Effects of spatial aggregation on the multi-scale estimation of evapotranspiration. Remote Sens. Environ. 2013, 131, 51–62. [Google Scholar] [CrossRef]
- Sharma, V.; Kilic, A.; Irmak, S. Impact of scale/resolution on evapotranspiration from Landsat and MODIS images. Water Resour. Res. 2016, 52, 1800–1819. [Google Scholar] [CrossRef] [Green Version]
- Small, C. The Landsat ETM+ spectral mixing space. Remote Sens. Environ. 2004, 93, 1–17. [Google Scholar] [CrossRef]
- Sousa, D.; Small, C. Global cross-calibration of Landsat spectral mixture models. Remote Sens. Environ. 2017, 192. [Google Scholar] [CrossRef]
- Carlson, T.N.; Gillies, R.; Perry, E. A method to make use of thermal infrared temperature and NDVI measurements to infer surface soil water content and fractional vegetation cover. Remote Sens. Rev. 1994, 9, 161–173. [Google Scholar] [CrossRef]
- Anderson, M.; Norman, J.; Mecikalski, J.R.; Torn, R.D.; Kustas, W.P.; Basara, J.B. A multiscale remote sensing model for disaggregating regional fluxes to micrometeorological scales. J. Hydrometeorol. 2004, 5, 343–363. [Google Scholar] [CrossRef]
- Anderson, M.; Kustas, W.; Norman, J.; Hain, C.; Mecikalski, J.; Schultz, L.; González-Dugo, M.; Cammalleri, C.; D’Urso, G.; Pimstein, A. Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrol. Earth Syst. Sci. 2011, 15, 223–239. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Nieto, H.; Kustas, W.P.; Torres-Rúa, A.; Alfieri, J.G.; Gao, F.; Anderson, M.C.; White, W.A.; Song, L.; Alsina, M.; Prueger, J.H.; et al. Evaluation of TSEB turbulent fluxes using different methods for the retrieval of soil and canopy component temperatures from UAV thermal and multispectral imagery. Irrig. Sci. 2018, 1–18. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Y. Estimating evapotranspiration fraction by modeling two-dimensional space of NDVI/albedo and day–night land surface temperature difference: A comparative study. Adv. Water Resour. 2011, 34, 512–518. [Google Scholar] [CrossRef]
- Galleguillos, M.; Jacob, F.; Prévot, L.; French, A.; Lagacherie, P. Comparison of two temperature differencing methods to estimate daily evapotranspiration over a Mediterranean vineyard watershed from ASTER data. Remote Sens. Environ. 2011, 115, 1326–1340. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.; Wooster, M.; Islam, S. A review of Ts/VI remote sensing based methods for the retrieval of land surface energy fluxes and soil surface moisture. Prog. Phys. Geogr. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Carter, C.; Liang, S. Comprehensive evaluation of empirical algorithms for estimating land surface evapotranspiration. Agric. For. Meteorol. 2018, 256–257, 334–345. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Johnson, P.E.; Smith, M.O.; Taylor-George, S.; Adams, J.B. A semiempirical method for analysis of the reflectance spectra of binary mineral mixtures. J. Geophys. Res. Solid Earth 1983, 88, 3557–3561. [Google Scholar] [CrossRef]
- Singer, R.B. Near-infrared spectral reflectance of mineral mixtures: Systematic combinations of pyroxenes, olivine, and iron oxides. J. Geophys. Res. Solid Earth 1981, 86, 7967–7982. [Google Scholar] [CrossRef]
- Singer, R.B.; McCord, T.B. Mars-large scale mixing of bright and dark surface materials and implications for analysis of spectral reflectance. In Lunar and Planetary Science Conference Proceedings; Pergamon Press: Houston, TX, USA, 1979; pp. 1835–1848. [Google Scholar]
- Kauth, R.J.; Thomas, G.S. The Tasseled Cap—A graphic description of the spectral-temporal development of agricultural crops as seen by Landsat. In Proceedings of the Symposium on Machine Processing of Remotely Sensed Data; Purdue University: West Lafayette, Indiana, 1976; pp. 4B41–4B51. [Google Scholar]
- Small, C. Multisource imaging of urban growth and infrastructure using Landsat, Sentinel and SRTM. In NASA Landsat-Sentinel Science Team Meeting; NASA: Rockville, MD, USA, 2018. [Google Scholar]
- Sousa, D.; Small, C. Multisensor analysis of spectral dimensionality and soil diversity in the great central valley of California. Sensors 2018, 18. [Google Scholar] [CrossRef]
- USGS Global Visualization Viewer (GloVis). Available online: https://glovis.usgs.gov/ (accessed on 4 December 2018).
- United States Geological Survey (USGS). Landsat 8 Data Users Handbook, Version 2.0; USGS: Sioux Falls, SD, USA, 2016.
- Gerace, A.; Montanaro, M. Derivation and validation of the stray light correction algorithm for the thermal infrared sensor onboard Landsat 8. Remote Sens. Environ. 2017, 191, 246–257. [Google Scholar] [CrossRef]
- Montanaro, M.; Gerace, A.; Lunsford, A.; Reuter, D. Stray Light Artifacts in Imagery from the Landsat 8 Thermal Infrared Sensor. Remote Sens. 2014, 6, 10435–10456. [Google Scholar] [CrossRef] [Green Version]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to broadband conversions of land surface albedo: I. Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Talsma, C.J.; Good, S.P.; Jimenez, C.; Martens, B.; Fisher, J.B.; Miralles, D.G.; McCabe, M.F.; Purdy, A.J. Partitioning of evapotranspiration in remote sensing-based models. Agric. For. Meteorol. 2018, 260–261, 131–143. [Google Scholar] [CrossRef]
- Talsma, C.J.; Good, S.P.; Miralles, D.G.; Fisher, J.B.; Martens, B.; Jimenez, C.; Purdy, A.J. Sensitivity of Evapotranspiration Components in Remote Sensing-Based Models. Remote Sens. 2018, 10, 1601. [Google Scholar] [CrossRef]
- Ramírez-Cuesta, J.M.; Allen, R.G.; Zarco-Tejada, P.J.; Kilic, A.; Santos, C.; Lorite, I.J. Impact of the spatial resolution on the energy balance components on an open-canopy olive orchard. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 88–102. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. Assessing the impact of end-member selection on the accuracy of satellite-based spatial variability models for actual evapotranspiration estimation. Water Resour. Res. 2013, 49, 2601–2618. [Google Scholar] [CrossRef] [Green Version]
- Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An intercomparison of the surface energy balance algorithm for land (SEBAL) and the two-source energy balance (TSEB) modeling schemes. Remote Sens. Environ. 2007, 108, 369–384. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P.; Li, Z.-L. How sensitive is SEBAL to changes in input variables, domain size and satellite sensor? J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Carlson, T.N. Triangle Models and Misconceptions. Int. J. Remote Sens. Appl. 2013, 3, 155–158. [Google Scholar]
- Sousa, D.; Small, C. Mapping and Monitoring Rice Agriculture with Multisensor Temporal Mixture Models. Remote Sens. 2018. submitted. [Google Scholar]
- Small, C. Comparative analysis of urban reflectance and surface temperature. Remote Sens. Environ. 2006, 104, 168–189. [Google Scholar] [CrossRef]
- Marshall, M.; Thenkabail, P.; Biggs, T.; Post, K. Hyperspectral narrowband and multispectral broadband indices for remote sensing of crop evapotranspiration and its components (transpiration and soil evaporation). Agric. For. Meteorol. 2016, 218–219, 122–134. [Google Scholar] [CrossRef]











| r2 = 0.9993, RMSE = 0.017 | r2 = 0.9994, RMSE = 0.079 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| aij | j = 0 | j = 1 | j = 2 | j = 3 | aij | j = 0 | j = 1 | j = 2 | j = 3 |
| i = 0 | 0.8106 | −0.5967 | 0.4049 | −0.0740 | i = 0 | 2.058 | −1.644 | 0.850 | −0.313 |
| i = 1 | −0.8029 | 0.7357 | 0.0681 | 0.2302 | i = 1 | −6.490 | 1.112 | −3.420 | −0.062 |
| i = 2 | 0.4866 | 1.2403 | −0.9489 | −0.8676 | i = 2 | 7.618 | 3.494 | 10.869 | 4.831 |
| i = 3 | −0.3702 | −1.3943 | −0.7359 | 0.3860 | i = 3 | −3.190 | −3.871 | −6.974 | −16.902 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sousa, D.; Small, C. Spectral Mixture Analysis as a Unified Framework for the Remote Sensing of Evapotranspiration. Remote Sens. 2018, 10, 1961. https://doi.org/10.3390/rs10121961
Sousa D, Small C. Spectral Mixture Analysis as a Unified Framework for the Remote Sensing of Evapotranspiration. Remote Sensing. 2018; 10(12):1961. https://doi.org/10.3390/rs10121961
Chicago/Turabian StyleSousa, Daniel, and Christopher Small. 2018. "Spectral Mixture Analysis as a Unified Framework for the Remote Sensing of Evapotranspiration" Remote Sensing 10, no. 12: 1961. https://doi.org/10.3390/rs10121961
APA StyleSousa, D., & Small, C. (2018). Spectral Mixture Analysis as a Unified Framework for the Remote Sensing of Evapotranspiration. Remote Sensing, 10(12), 1961. https://doi.org/10.3390/rs10121961