Next Article in Journal
Terrestrial CDOM in Lakes of Yamal Peninsula: Connection to Lake and Lake Catchment Properties
Next Article in Special Issue
Metrology Assessment of the Accuracy of Precipitable Water Vapor Estimates from GPS Data Acquisition in Tropical Areas: The Tahiti Case
Previous Article in Journal
High-Chlorophyll-Area Assessment Based on Remote Sensing Observations: The Case Study of Cape Trafalgar
Previous Article in Special Issue
CloudSat-Based Assessment of GPM Microwave Imager Snowfall Observation Capabilities
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 10
Issue 2
10.3390/rs10020166
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Stable Water Isotopologues in the Stratosphere Retrieved from Odin/SMR Measurements

by
Tongmei Wang
1,2,*,
Qiong Zhang
1,
Stefan Lossow
3,
Léon Chafik
4,
Camille Risi
5,
Donal Murtagh
6 and
Abdel Hannachi
2
1
Department of Physical Geography, Stockholm University, 10691 Stockholm, Sweden
2
Department of Meteorology, Stockholm University, 10691 Stockholm, Sweden
3
Institute for Meteorology and Climate Research, Karlsruhe Institute of Technology, 76021 Leopoldshafen, Germany
4
Geophysical Institute, Bjerknes Center for Climate Research, University of Bergen, 5020 Bergen, Norway
5
LMD/IPSL, CNRS, 75005 Paris, France
6
Department of Earth and Space Sciences, Chalmers University of Technology, 41296 Gothenburg, Sweden
*
Author to whom correspondence should be addressed.
Remote Sens. 2018, 10(2), 166; https://doi.org/10.3390/rs10020166
Submission received: 16 November 2017 / Revised: 18 January 2018 / Accepted: 23 January 2018 / Published: 25 January 2018
(This article belongs to the Special Issue Remote Sensing Water Cycle: Theory, Sensors, Data, and Applications)
Browse Figures
Versions Notes

Abstract

:
Stable Water Isotopologues (SWIs) are important diagnostic tracers for understanding processes in the atmosphere and the global hydrological cycle. Using eight years (2002–2009) of retrievals from Odin/SMR (Sub-Millimetre Radiometer), the global climatological features of three SWIs, H216O, HDO and H218O, the isotopic composition δD and δ18O in the stratosphere are analysed for the first time. Spatially, SWIs are found to increase with altitude due to stratospheric methane oxidation. In the tropics, highly depleted SWIs in the lower stratosphere indicate the effect of dehydration when the air comes through the cold tropopause, while, at higher latitudes, more enriched SWIs in the upper stratosphere during summer are produced and transported to the other hemisphere via the Brewer–Dobson circulation. Furthermore, we found that more H216O is produced over summer Northern Hemisphere and more HDO is produced over summer Southern Hemisphere. Temporally, a tape recorder in H216O is observed in the lower tropical stratosphere, in addition to a pronounced downward propagating seasonal signal in SWIs from the upper to the lower stratosphere over the polar regions. These observed features in SWIs are further compared to SWI-enabled model outputs. This helped to identify possible causes of model deficiencies in reproducing main stratospheric features. For instance, choosing a better advection scheme and including methane oxidation process in a specific model immediately capture the main features of stratospheric water vapor. The representation of other features, such as the observed inter-hemispheric difference of isotopic component, is also discussed.

Graphical Abstract

1. Introduction

Stratospheric water vapor plays a critical role in the climate system. Changes in stratospheric water vapor affect the fluxes of longwave (infrared) and shortwave (solar) radiation, and thereby influence the temperature in the stratosphere and troposphere [1,2]. Studying the current and future distribution and variability in stratospheric water vapor on a global scale is helpful for our understanding of climate change. For atmospheric and hydrologic sciences, besides the most abundant water isotopologue H216O (hereafter H2O), which is called normal or light water, there are two most relevant kinds of heavy water, HD16O (hereafter HDO) and H218O. These three stable water isotopologues (hereafter designated by water isotopes or SWIs) have slightly different physical and chemical properties and thus require different latent energy for water phase changes, i.e., fractionation: light water preferentially evaporates, and heavy water preferentially condenses. The concentration of water isotopes varies typically during its phase changes. The processes related to water vapor in the atmosphere leave an isotopic fingerprint in the respective water vapor compound [3]. The knowledge of the spatial and temporal distribution of the different SWIs is of great interest for a better understanding of the processes controlling the water vapor behavior in the atmosphere [4]. For example, the vertical distribution of water vapor in the lower stratosphere provided evidence for a world circulation, the Brewer–Dobson Circulation (BDC) [5,6]. Other dynamic processes in the troposphere, e.g., deep convective overshooting such as strong Inter-Tropical Convergence Zone (ITCZ) and Northern Hemisphere monsoon circulations during boreal summer, may contribute much to the changes in upwelling from the troposphere to the stratosphere [7,8], influencing therefore the concentration and distribution of the stratospheric water including its isotopologues. The SWIs data provide a valuable tool to study the transport of tropospheric water into the lowermost stratosphere [9]. Besides the dynamical processes, chemical reactions in the middle atmosphere play important role on stratospheric SWIs, mostly through the methane oxidation. Methane is oxidized in the middle atmosphere by reactions with OH, Cl, and O(1D), and by photolysis [10,11]. The reaction with OH is the most important mechanism in the upper troposphere and lower stratosphere (UTLS). In the stratosphere, at around 30 km height, the reaction with O(1D) is also significant and becomes more important than the reaction with OH in the upper stratosphere above 50 km. In the upper stratosphere, photolysis of methane produces CH3 and H, and further reactions produce water [12]. The isotopic composition of HDO distribution in the middle atmosphere is expected to mirror the partitioning of the different CH4 oxidation reactions [4]. More than 99% of all oxygen atoms taken to form H2O in the middle atmosphere stem from the hydroxyl radical OH, hence, the composition of H218O also provides information on the oxygen isotope composition of OH [13].
With the development of satellite remote sensing technology, space measurements of stratospheric SWI have become available to the climate community for exploration. The first satellite-derived SWIs data were obtained by the ATMOS (Atmospheric Trace Molecular Spectroscopy) instrument, which measured isotopic composition in the upper troposphere and stratosphere on four short-term missions in the 1980s and 1990s [14]. The ATMOS measurements were performed on different occasions and therefore have no global coverage. In 2000, the TES (Tropospheric Emission Spectrometer) provided measurements of the tropospheric HDO and H2O, which were used to calculate the isotopic composition of HDO, δD [15], i.e., the departure from the standard composition. This resulted in an unprecedented global scale perspective of the tropospheric isotopic depletion of water vapor. In recent years, three satellite missions collected data retrieving stratospheric SWIs: the MIPAS (Michelson Interferometer for Passive Atmospheric Sounding) instrument on Envisat (Environmental Satellite) allowed for H2O and HDO retrievals from July 2002 to March 2004, roughly at the altitude range between 10 and 50 km [16]. The 19-month observation record from the MIPAS revealed a clear seasonal cycle signal and transport of SWIs into the stratosphere [17,18]. The measurements of normal and deuterated water from the ACE-FTS (Atmospheric Chemistry Experiment Fourier Transform Spectrometer) were used to map global climatological behavior of HDO along with the HDO/H2O ratio in the upper troposphere- lower stratosphere, but for this dataset measurements were made in the tropics only during February, April, August and October [19]. Recently, a particularly rich source of SWIs, with vertical coverage reaching the mesosphere, has been retrieved from the measurements by SMR (Sub-Millimetre Radiometer) aboard the Odin satellite since 2001 [20]. Odin/SMR SWIs data have much longer time span than, e.g., MIPAS, and higher than, e.g., ACE-FTS, which retrieves HDO from 6.5 to 37.5 km in altitude [21]. These invaluable data have not been fully explored to study the stratospheric isotopic structures, atmospheric hydrological cycle and related dynamical processes.
In recent decades, SWIs were incorporated in general circulation models (GCMs) to improve the understanding of hydrological cycles at different scales. GCM simulations show that the distribution of water isotopes is sensitive to the parameterization of cloud physics and the representation of upper tropospheric processes, and are therefore useful in constraining modeled cloud physics and investigating the mechanisms of stratosphere–troposphere exchange of water vapor [22]. Most GCMs use very similar formulations for the isotopic fractionation, notwithstanding the diversity of their underlying physical parameterizations. An SWI Intercomparison Group (SWING) project has been initiated to evaluate the atmospheric hydrological processes in GCMs based on water isotopes [23]. Large differences in water isotopes in the troposphere and in precipitation have been found between observations and model simulations [24,25,26]. Therefore, the comparison of simulated water isotopes with the satellite data is valuable for evaluating the ability of GCMs to represent stratospheric processes.
This work first presents a basic understanding of stratospheric processes in three-dimensional spatial distributions of SWIs. The observed features in SWIs are further compared to SWI-enabled model outputs, to evaluate the ability of climate model in simulating stratospheric processes. Section 2 introduces the data and methods. Section 3 discusses the SWI climatology, i.e., the vertical and horizontal distributions, the seasonal cycle, and the vertical propagation. Section 4 compares the simulations from SWI-enabled models. We use one model LMDZ4 [27] to perform specific experiment for identifying what cause the defects in SWING2 models. Section 5 presents discussions. Conclusions are provided in Section 6.

2. Data and Method

The Odin satellite is part of a Swedish-led mission aimed at obtaining observations of trace gas profiles in the stratosphere and mesosphere [28]. The satellite was launched on 20 February 2001 with a two-year mission plan but remains operational until today. Odin follows a quasi-polar sun-synchronous orbit at around 600 km altitude. Measurements are typically performed along the orbital track, resulting in a latitudinal coverage between 82°S and 82°N. Odin carries two instruments, one of them is the Sub-Millimetre Radiometer (SMR), which consists of five radiometers that cover several frequency bands between 486 GHz and 581 GHz and around 119 GHz, observes several thermal emission lines at the atmospheric limb using a 1.1 m telescope. Stratospheric H2O, H218O and HDO information are obtained from emission lines centered at 488.5 GHz, 489.1 GHz and 490.6 GHz, respectively [29]. For technical reasons (maximum bandwidth of a single radiometer is only 0.8 GHz) not all three isotopologues but just H2O and H218O can be measured at the same time. Typically, the H2O and H218O observations are performed in an alternating manner with those of HDO with one orbit covering the former two, followed by another covering the HDO emission line. The typical single-scan precision of the SWIs measurements H2O, H218O and HDO are 5–15%, 10–20% and 10–20%, respectively [29]. As SMR has a multitude of measurement targets and modes, the stratospheric SWIs are not observed on a daily basis. Until April 2007 the typical observation frequency was 3–4 days per month. After that the astronomy observations ceased, the observation frequency increased to 8–9 days per month. The atmosphere is typically sampled in the altitude range between 7 km and 110 km with an effective vertical sampling of 3 km. Such scan takes about 140 s, which corresponds to a horizontal sampling of one scan per 1000 km.
SWIs retrieved from Odin/SMR measurements can be used for the study of the water cycle in the stratosphere at minimum height above 20 km from the Earth surface, where data with sufficient quality can be retrieved. Here we focus on observations made during the period 2002–2009. Later observations suffer from calibration and retrieval issues, in particular for HDO. These issues are currently under investigation to make the later observations available for future studies.
Figure 1 shows an example of the sampling coverage by Odin in January 2003. The data are measured over limited regions due to the scanning interval. The data used here were retrieved using the official Odin/SMR retrieval processor (version 2.1) at the Chalmers University of Technology in Gothenburg/Sweden [30]. The monthly mean values are re-gridded onto a 5° × 5° lat-lon grid. A few outliers, given by volume mixing ratios outside reasonable boundaries, were removed by filtering according to the median and median absolute deviation [31]. Here, we consider data in the altitude range between 20 km and 60 km to explore the features of SWIs in the stratosphere and their relationships with stratospheric circulation.
Besides SWIs, we also consider the air temperature from NASA’s MERRA (Modern-Era Retrospective Analysis for Research and Applications) reanalysis data [32], which reaches the mesosphere and facilitates a better comparison with satellite measurement and TOA (Top Of Atmosphere) incident shortwave radiation, which is derived from the total solar irradiance instrument aboard the SORCE (Solar Radiation and Climate Experiment) satellite [33].
The isotopic ratio R used here for a given sample is expressed as the ratio between the heavy water isotopes (HDO and H218O) and the major water isotope H2O, i.e., for HDO, R = [HDO]/[H2O], and for H218O, R = [H218O]/[H2O].
The internationally accepted standard for measurements of deuterium and oxygen isotopic composition of natural water samples is Vienna Standard Mean Ocean Water (VSMOW) [34], as RVSMOW. The isotopic compositions of HDO and H218O are typically expressed in per mil (‰) as the departure from the standard composition, using:
δ = ( R s a m p l e R V S M O W − 1 ) × 1000
Rsample is the ratio of the sample of the atmospheric water vapor measured by Odin/SMR. RVSMOW is 2.0052 × 10−3 for H218O and 3.1152 × 10−4 for HDO.
Equation (1) provides the per mil enrichments of the isotopic ratios relative to the mean ocean water standard. Negative (positive) values of δ mean depletion (enrichment) of heavy isotope HDO or H218O.

3. Climatology of the SWIs in the Stratosphere

3.1. Global Mean Vertical Profiles

Figure 2 shows the climatology of global mean vertical profiles of the water isotopic composition along with their standard deviations. The vertical profile of H2O exhibits an irregular decrease with altitude in the lower stratosphere up to approximately 25 km, an increase from 25 km to 50 km, and then a decrease above 50 km. Similar profiles are obtained for HDO and H218O (not shown). Lossow et al. [35] compared HDO data from MIPAS with that of Odin/SMR and ACE-FTS and demonstrated a high consistency in the structures above 20 km between all three instruments. Even where the MIPAS HDO retrieval reaches its limits (above 40 km), there is still good agreement between HDO from MIPAS and Odin/SMR, pointing to the fact that data from different satellites can complement each other to some extent. The profiles of δD and δ18O are shown in Figure 2b. The global mean δD (blue in Figure 2b) is about −650‰ in the lower stratosphere and increases to −350‰ near the stratopause at approximately 50 km. However, δ18O (purple in Figure 2b) shows enrichment (relative to VSMOW) above 35 km.
This increase with altitude is due to the chemical generation of water vapor [10]. The chief corresponding chemical reactions are between methane and hydroxyl radical (OH), chlorine (Cl), singlet oxygen (O1D) and photons (hv) [11]:
CH4 + OH → CH3 + H2O
CH4 + Cl → HCl + CH3
CH4 + O(1D) → CH2 + H2O
CH4 + hv → CH3 + H
The product of HCl of Equation (3) produces water in a second reaction:
HCl + OH → Cl + H2O
The reaction with OH (Equation (2)) is the most important mechanism in the upper troposphere and lower stratosphere (UTLS). The reaction with O(1D) (Equation (4)) is significant in the middle stratosphere and becomes more important than the reaction with OH in the upper stratosphere. The photolysis of methane (Equation (5)) produces CH3 and H in the upper stratosphere, and further reactions produces water [12] as:
CH3 + H → CH2 + H2
CH3 → CH2 + H
H2 + OH → H+ H2O
H + HO2 → O + H2O
Therefore, the production of water through methane oxidation is stronger in the upper stratosphere [36]. Here, we show the reactions that start with CH4. If the methane is not CH4 but CH3D, the reactions produce HDO. The oxygen could be any of the oxygen isotopes, e.g., 17OH, 18OH, 17O(1D) or 18O(1D), which is not highlighted here. A detailed description of the initial methane destruction reactions can be found in Bechtel and Zahn (2003) [4].
Studies dealing with SWI in the upper troposphere and lower stratosphere have previously indicated that there is strong dehydration and isotopic depletion near the cold-point of the tropopause [8,37,38,39], while above the tropopause, more water is produced owing to different chemical processes. However, because the saturation pressure of water vapor is large due to the increase in temperature with altitude, water vapor rarely condenses in the stratosphere with the exception of polar stratospheric clouds during winter. The maximum of H2O is around the stratopause, but δD and δ18O increase even above the stratopause since H2O decreases more than HDO and H218O with the altitude above 50 km.
Figure 2c shows the standard deviation of H2O. The minimum variation occurs around the middle stratosphere, greater variation is in the lower stratosphere below 30 km, and maximum variation is in the upper stratosphere around 50 km. Figure 2d shows larger inter-annual variability of δD and δ18O in the upper stratosphere above approximately 40 km than in the middle stratosphere, which is possibly due to the large variability in H2O (Figure 2c). In the lower stratosphere, the variability of HDO and H218O become large (not shown) and contributes significantly to the variability of δD and δ18O.

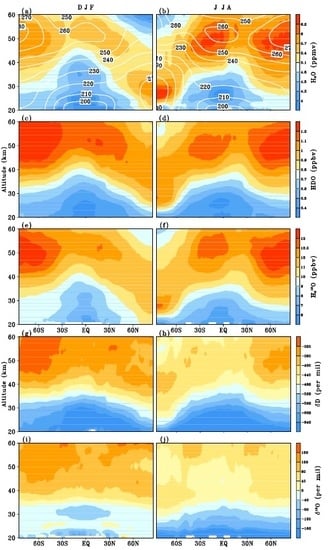
3.2. Zonal Mean Structure in the Lower and Upper Stratosphere

Based on the different features of the vertical profiles in Figure 2, we divide the stratosphere into three layers: low (20–30 km), middle (30–40 km) and high (40–50 km) levels. The zonal mean structure of the climatologies of H2O, δD and δ18O along with their standard deviation at different levels in the stratosphere are shown in Figure 3. The general feature of the zonal mean distribution shows a quasi-equatorial symmetric pattern in water isotopes (Figure 3a, note that only H2O is shown, the distributions of HDO and H218O are similar). In the lower stratosphere, the lowest SWI value is around the equator, reflecting the higher tropopause in this region, the associated dehydration, and the increase in aged air at higher latitudes [40]. The higher tropopause is also reflected by the lowest SWI value in the middle and upper stratosphere. We will discuss this more in Section 3.3. High SWI values are observed over high latitudes for two main reasons: (i) the downwelling of the very deep branch of the BDC during winter bringing down older air from the upper level, in addition to more moist air from summer hemisphere where methane oxidation produces new water; and (ii) the enhanced methane oxidation producing more water during summer when there is high insolation. Figure 3a also shows that the meridional (equator-ward) gradient is steeper in the lower stratosphere compared to the upper stratosphere, which is due to a stronger meridional transport in the upper stratosphere as suggested by Holton et al. [41]. Figure 3b shows an interesting feature related to the stronger inter-annual variability in the upper layer compared to the lower layer. We consider this is related to the variability of the chemical processes, which produce more water in the upper stratosphere. The exchange between the stratosphere and the troposphere affects the variability in the lower stratosphere. Between these two layers, some influences from both layers counteract each other, leading to a relatively weak variability in the middle stratosphere.
The zonal mean climatology of δD and δ18O are shown in Figure 3c,e, respectively. Similar quasi-equatorial symmetric structures are observed in the upper, middle and lower stratosphere, with a minimum over the tropics and a maximum over high latitudes. The value of δD varies from −670‰ to −540‰ in the lower stratosphere and from −390‰ to −330‰ in the upper stratosphere. The value of δ18O changes from negative to positive as we go from the lower to the upper stratosphere. There is relatively less depletion in δD and δ18O around 10°N–20°N. A clearly pronounced peak shows up in the lower stratosphere in δD (the blue curve in Figure 3c) and in δ18O (Figure 3e). This latitudinal band corresponds to the location of the ITCZ and the monsoons in boreal summer. Monsoons have a significant impact on stratosphere–troposphere exchange, and on the entry of air into the stratosphere. Previous analyses indicate that the Asian monsoon circulation can contribute up to 75% of the total net upward water vapor flux in the tropics at the tropopause in boreal summer [7], yielding more water vapor into the stratosphere over the region. The standard deviation of δD and δ18O (Figure 3d,f) shows much stronger variability in the upper and lower stratosphere where more chemical and dynamical processes are involved, similar to what was explained for the standard deviation of H2O before. In the middle level, the variabilities of δD and δ18O are weaker.

3.3. Seasonal Cycle and Related Processes

We now discuss the seasonal mean distribution of water isotopes and their compositions. Figure 4 shows the seasonal mean climatologies in the meridional cross section of SWIs. We use the mean of December, January and February (DJF) to represent austral summer mean and the mean of June, July and August (JJA) to represent boreal summer. As expected, the three isotopes have similar structures. Consistent with the global mean vertical profiles shown in Figure 2, the mixing ratios of the SWIs all increase with height at each latitude. Low values are observed in the lower stratosphere centered over the tropics resulting from the dehydration that occurs when the air travels through the tropopause, as mentioned in Section 3.1. Maximum values in the upper layers occur at high latitudes of summer hemisphere, reflecting again the production of water vapor through methane oxidation under a long duration of sunlight. In addition, we can clearly see water vapor transport from the upper level over the summer polar region down to the lower level over winter polar region, leading to a maximum over winter hemisphere at approximately 25–35 km. This cannot be explained by local water production because there is almost no sunlight; rather, it can be attributed to the inter-hemispheric transport of water vapor along the upper branch of the BDC [42] and the downward transport of moist air within the winter polar vortex.
In Section 3.2, we point out that the lowest SWI value over the tropics reflects the higher tropopause in this region. Although in Figure 4 the tropopause level cannot be seen, its extended distribution is reflected by the temperature (contour in Figure 4a,b) and SWIs: the coldest air is over the tropics; and the minimum value of SWIs over the tropics is in the lower stratosphere. This reflection in SWIs even reaches 50 km in both summer hemispheres: the bell-shaped SWIs clearly reach the upper stratosphere and tilt slightly to summer hemisphere with increasing altitude. We consider this to be related to a shift in the deep convection, for example the ITCZ always shifts to the summer hemisphere. The relevant processes, e.g., mass transport up to the stratosphere and the related dehydration, also shift to the summer hemisphere. These hydrologic related processes are much more clearly reflected in SWIs than in temperature.
For the global structure and seasonality, Figure 4 shows another character of stratospheric H2O, namely a center of high isotope values is over winter hemisphere in the lower stratosphere, compared with the upper stratosphere. This center is also apparent from a 19-month length data set retrieved from MIPAS [17] (see Figure 3 in [17]). Other satellite water vapor data from UARS HALOE (Halogen Occultation Experiment on the Upper Atmosphere Research Satellite) with vertical coverage from 100 hPa to 0.32 hPa (approximately 16–56 km) and time span for 1991–1997 also showed similar distribution of the stratospheric H2O [43] (see Figure 7 (January and July) in [43]). This coherent character is related to the winter polar vortex: Water vapor transferred from the summer hemisphere in the upper stratosphere was pushed down to the lower stratosphere by the winter polar vortex. Beside this, the Odin/SMR data also show more H2O produced during the boreal summer (JJA mean) than during the austral summer (DJF mean), which has not been observed in HALOE and MIPAS. The value of HDO over south polar region in austral summer is larger than that over north polar region; this situation is opposite to that of H2O. No significant inter-hemispheric difference is observed for H218O.
Figure 5 shows that δD and δ18O have similar distributions to that of the water vapor mixing ratios, but there are some differences observed in the isotopic ratios. Figure 5 shows the large water isotopes depletion in the lower stratosphere, indicating that the vertical transport is associated with ascending air over the tropics and subtropics penetrating the cold tropopause. In the upper stratosphere water vapor is mostly produced during methane oxidation, and enriched heavy water means that this water is more abundant in the newly produced water vapor than in the old water, which was in the stratosphere before, and the water came from the troposphere. The heavy isotopes are more enriched over the south polar region in the austral summer (Figure 5a,c) than over the north polar region in boreal summer (Figure 5b,d). This is mainly because H2O is produced more during boreal summer than austral summer.
In contrast, the depletion of H218O in the lower stratosphere is more pronounced in the JJA mean (less than −200‰). Previous studies show that deep convective, such as strong ITCZ and Northern Hemisphere monsoon circulations during boreal summer, contribute much to the changes in the upwelling from the troposphere to the stratosphere [7,8]. This provides a natural link to the H218O depletion.
Water production through chemical processes occurs mainly in the middle and upper stratosphere, as indicated by a pronounced increase in SWIs at high latitudes in summer hemisphere. This production of water relates to the higher level of solar radiation in those regions. The newly produced water can be transported to winter hemisphere through BDC, and then transferred downward to the lower stratosphere due to the winter polar vortex. The structure of SWIs follows the distribution of temperature very well over summer hemisphere, with high amounts of SWI associated with high air temperature, notably in the upper stratosphere due to the ozone absorption of solar radiation, suggesting a close connection between SWIs and solar radiation.
Figure 6 shows a scatter plot of the relationship between the mixing ratio of H218O in the upper stratosphere and the solar irradiance of summer hemisphere. It suggests further support in favor of the effect of solar radiation on H218O in summer hemisphere. A monotonic linear association between H218O and solar radiation level, as reflected by the correlation coefficient of 0.80 (above 1% significance level), indicates that the oxidation process is closely related to the level of solar radiation. The same significant positive correlation exists between solar radiation level and the two other SWIs (H2O and HDO, not shown).

3.4. Vertical Propagation of Seasonal Signal

Two distinct features of water isotopes can be identified in Figure 4, namely the low mixing ratios in the lower stratosphere, centered over the tropics, and high values in the upper stratosphere over high latitudes. Figure 7 and Figure 8 display the details of the seasonal cycle with a particular focus on the tropical and polar regions. The figures show the monthly time evolution of SWIs and their composition anomaly over the tropics (15°S–15°N mean) and south polar region (60°S–85°S mean).
The H2O anomaly over the tropics in Figure 7 shows an interesting phenomenon in the lower stratosphere occurring between 20 and 30 km, wherein a minimum in H2O signal propagates upwards from November of a given year, reaching 30 km in May of the following year. Furthermore, a maximum in water vapor signal propagates upwards from 20 km in May to approximately 30 km in September. This feature is more pronounced than that found in MIPAS data [17]. The propagation in the tropics is consistent with results from previous studies, known as the tropical tape recorder signature, which was seen in some satellite observations and model simulations [18,19,44,45]. No such propagation is found in the heavy isotopologues, (HDO and H218O), or in isotopic compositions δD and δ18O (not shown), which could be because, in the lower stratosphere, the content of heavy water is too small after the dehydration (heavy water preferentially condenses), and so a signal of heavy water is too weak to be observed.
Figure 8 shows a pronounced signal of seasonal change over the south polar region, propagating downwards from the stratopause to the lower stratosphere in all three water isotopes and δD, but not obvious for δ18O (not shown). In Figure 8, the positive (negative) anomalies always propagate from 50 km in summer (winter), down to 30 km in winter (summer) where the signal is strengthened and carried further down. This strengthening is related to the inter-hemispheric transport and downwelling from the winter polar vortex. The propagation is more marked in the heavy (Figure 8b,c) than in the light (Figure 8a) isotopes. Such a pattern is associated with the heavy water that is more abundant in the upper than in the lower level of the stratosphere. The pattern over the north polar region (60°N–85°N mean) is similar to that over the south polar region and therefore is not shown here.

4. Comparison with SWI-Enabled GCM Simulation

To complement the above exploratory analysis, the aim of this section is to evaluate key stratospheric processes related to water isotopes as represented by Global Climate Models (GCMs). GCM simulations show that water isotopes are sensitive to the parameterization of cloud physics and the representation of upper tropospheric processes [22]. Thus, GCMs offer a suitable tool to constrain modeled cloud physics and investigate the mechanisms of stratosphere–troposphere exchange of water vapor [22]. Currently, SWIs are implemented in several GCMs [46]. Model data comparison reveals a quite large spread of GCMs regarding isotopic behavior that is not obviously related to moisture [24], and thus observations of water vapor isotopes can be used to explore model deficiencies in simulating water isotopes and identify key parameterization.
We used the available Odin/SMR data to evaluate how well the models perform in simulating stratospheric stable water isotopes. At first, we select one of the SWING2 models, namely LMDZ4, for running sensitivity experiments in an attempt to better understand what controls the stratospheric SWIs. The LMDZ4 model was developed at the Laboratorie de Météorologie Dynamique [27] with water isotopes implementation, and can reproduce the spatial patterns of water isotopes in the troposphere reasonably well [24,47]. The model is the atmospheric component of the Insitut Pierre-Simon Laplace coupled model (IPSL-CM4) [48] used in Coupled Model Intercomparison Project phase3 (CMIP3). It is used here with a 2.5° × 3.75° latitude longitude resolution, and 39 vertical levels from the surface to near 65 km. The physical package includes the Emanuel convective scheme [49] and a statistical cloud scheme [50]. The isotopic version of LMDZ4 is described in detail by Risi et al. [47]. The experiments were performed with LMDZ4 for the 2002–2009 period, nudged with the European Centre for Medium-Range Weather Forecasts (ECMWF) operational analyses [51].
The first experiment (Exp1) was run with a second-order monotonic finite volume advection scheme [52]. A simple parameterization of methane oxidation was implemented, which represents roughly key chemical processes in the stratosphere. This implementation is based on a similar methane parameterization used in the ECMWF Integrated Forecasting System (IFS) following Brasseur and Solomon [53]. To represent the stratospheric processes, we ran the stratospheric version of LMDZ4 (LMDZ4strato) [54], with options activated to improve the stratosphere.
Figure 9 shows the seasonal mean water isotope H2O (the patterns of HDO and H218O are similar and not shown here), δD, and δ18O simulated in LMDZ4 Exp1. Compared with the Odin/SMR data (Figure 4 and Figure 5), LMDZ4strato Exp1 has a dry bias. The dry bias seems to be a systematic bias in all GCMs (shown later in Figure 11). Another difference between Exp1 and the observed values is the large values in the lower stratosphere in winter hemisphere over high latitude regions, which are apparent in Odin/SMR (Figure 4a,b) but do not appear in the LMDZ4strato simulation (Figure 9a,b), where the large values are replaced by low values in the JJA mean (Figure 9b). This may be associated with the dynamical transport in the model, which needs further evaluation.
Despite these two discrepancies, Figure 9a,b shows quite similar patterns to the Odin/SMR data (Figure 4a,b) in the stratospheric SWIs: the bell-shaped low value in the lower stratosphere is nearly symmetric about the equator and slightly tilts to summer hemisphere with altitude and the maximum value appears in the upper stratosphere in the summer polar region. The hemispheric difference is also reproduced in Exp1: more water produced over the Northern Hemisphere during boreal summer than over the Southern Hemisphere during austral summer, although the differences are not as large as in the Odin/SMR data.
The isotopic compositions δD and δ18O in Figure 9c–f show similar patterns to Figure 5: the lowest value is over the tropics in the lower stratosphere; isotopic ratios increase with altitude; the maximum is over summer polar region, around the stratopause; and the second-highest ratio is over the winter hemisphere due to inter-hemispheric transport. The heavy isotopic ratios calculated from the simulation are much lower than the observed ratios. Unlike the observation, the simulation does not show more enrichment of heavy water in the upper stratosphere during the austral summer compared to the boreal summer. It is approximately equal for the two seasons. This is because the difference in produced H2O between the two seasons in the simulation is not as great as in the observations.
To examine the vertical transfer of the seasonal cycle signal in the simulation, the temporal evolution of the H2O anomaly over the tropics and the south polar region is shown in Figure 10. To show the vertical exchange between the stratosphere and the troposphere clearly, Figure 10 is plotted from 15 km. Compared with Figure 7, Figure 10a shows a very clear tape recorder in the upper troposphere and lower stratosphere over the tropics. In general, the upward propagation of the wet anomaly starts from 15 km in July and reaches 25 km in January. The propagation of a dry anomaly has the opposite phase of a wet anomaly and propagates from 15 km in January to 25 km in July (except during 2007 when the wet anomaly is seen to persist below 25 km throughout the year). Above 25 km, the wet and dry anomaly is found around July and January, respectively. Over the polar region, Figure 10b shows a downward transfer of the moisture signal over the polar region from the upper stratosphere (around 55 km) in summer to the middle stratosphere (around 35 km) in winter. Meanwhile, the dry anomaly is more stable on some layers in certain seasons: it is in the upper and lower stratosphere during winter and in the middle stratosphere during summer. Compared with the observations (Figure 8), this indicates that LMDZ4strato does not capture the downward transfer over the polar regions very well.
Apart from LMDZ4, other simulations are available (see model details in Table 1 in [24]) in the SWING2 intercomparison project (http://data.giss.nasa.gov/swing2/). Most of these models have vertical coverage up to 10 hPa (approximately 30 km). The model outputs were used to analyze tropospheric humidity [24]. Here, we choose three model simulations to analyze the stratospheric SWI distributions: GISS modelE [55] and GSM [56] were nudged by reanalysis data, while MIROC [57] was free-running. “Free-running” means that it is the standard AMIP-style simulations [58] forced by observed sea surface temperatures, and their winds are not nudged. Figure 11 shows the zonal mean vertical profile of H2O simulated from 2002 to 2009. Compared with Odin/SMR, despite the difference in value magnitude, the GISS model (Figure 11a,b) reproduced the main features of H2O: H2O increases with altitude, with a bell-shaped minimum value over the tropics and maximum value over the polar regions. However, some details in observations, e.g., the large values in the lower stratosphere in winter hemisphere over high latitude regions, are missing from the GISS simulation, similar to the situation of the LMDZstrato Exp1. Other models, such as the GSM model (Figure 11c,d) and the MIROC model in DJF (Figure 11e), reproduced the vertical structure over the tropics: the minimum ratio is over the tropics and it increases with altitude. The gradient from the tropics to the extratropics is too strong, and the water ratio over the extratropics decreases with altitude, unlike the observations. The simulation of the MIROC model in JJA is worse than in DJF (Figure 11f), barely indicating that the minimum is over the tropics. For all these models, simulation of DJF is better than that of JJA.
To understand what causes the defects seen in the SWING2 models, two sensitivity tests that deliberately degraded the model were performed. For one sensitivity experiment (Exp2), we kept everything the same as Exp1, but removed the methane oxidation. Another sensitivity experiment (Exp3) was based on Exp2, but we used a simple upstream numerical scheme [59] instead of the second-order monotonic finite volume advection scheme.
Here, we show the zonal mean H2O vertical structure from two experiments (HDO and H218O have similar structures, not shown here). In Exp2 (Figure 12a,b), without the methane oxidation implementation, the dry bias in the stratosphere is much more severe than in Exp1 (Figure 9a,b). Briefly, the increase of H2O with altitude is similar to the observations and Exp1. However, in the lower stratosphere, the minimum (dry) center, which is around the equator in Exp1, shifts to the Southern Hemisphere in both seasons, and it is very strong over polar region in the JJA mean. This strong dry center also appears in other SWING2 models in JJA mean, for example in GSM. Compared with Figure 4b, even though the GISS model (Figure 11b) and LMDZstrato Exp1 (Figure 9b) improved significantly the pattern, we can still see the dry center over the southern high latitude in the lower stratosphere in JJA mean H2O.
Furthermore, from Exp3 with a simple upstream scheme (Figure 12c,d), we identify a strong wet bias in the lower stratosphere over the extratropics. This strong moisture bias also appears in other SWING2 models with model top in the lower stratosphere (Figure 11c–f). Due to the moisture bias in the lower stratosphere, the simulated H2O decreases with altitude over the extra-tropics poleward of 20°, which is nearly the opposite of the observed pattern. This moisture bias is more severe in the GSM model [56], attributed to an overly diffusive advection scheme [25]. When the diffusion scheme was modified in Exp2, the pattern was largely improved. Further implementation of CH4 oxidation in Exp1 led to a much better agreement with observations, as demonstrated in Figure 9a,b.
The model data comparison above suggests that, to better represent the physical and dynamical processes of the stratosphere, increasing the model top to the upper stratosphere and implementing methane oxidation are necessary steps for obtaining a good simulation of the upper stratospheric structure. In addition, the advection scheme requires some care to overcome the large moisture biases in the lower stratosphere in the extra-tropics.

5. Discussion

Since the retrieved Odin/SMR data reaches the stratopause, it provides a valuable tool to investigate how water isotopic structure can be used to evaluate the dehydration, the methane oxidation and the atmospheric transport in the stratosphere. The obtained tape recorder in the lower stratosphere over the tropics, demonstrating that the retrieved data, from a minimum distance of 20 km above the Earth’s surface, have sufficient good quality to observe changes in mixing ratios caused by seasonal changes in tropics.
The distributions of the seasonal and zonal mean isotopic ratios show that normal water vapor H2O is more abundant during boreal summer than austral summer. This feature does not show up in the HALOE or MIPAS, and we suggest that the process of methane oxidation is responsible for it. This, however, remains an open question and needs further investigation, which is left for future research.
It is the first time that stratospheric observations (retrievals) from satellite data include H218O. The accurate measurement of the H218O by remote-sensing techniques remains a challenge due to the atomic mass difference between 18O and 16O. The H218O from Odin/SMR retrievals are valuable to explore, despite possible uncertainties both in measurement and retrieval method. They also provide the potential to examine the relationship between δD and δ18O. Previous studies show that the δD and δ18O in surface precipitation are linearly related and can be fit to the equation [60] as,
δD = 8 × δ18O − d-excess
where d-excess is deuterium excess parameter [61], which is in general analyzed in relation to the study of isotopes in precipitation or in tropospheric water vapor. Based on GNIP data, the proportion of d-excess in modern precipitation records is approximately 10‰ [60], called the Global Meteoric Water Line (GMWL) and can be used as a reference in the hydrological studies.
In the stratosphere, fractionation takes place mostly via chemical reactions, not the phase changes as in the troposphere. SWIs are mainly related to chemistry and dynamics in the stratosphere. For example, water isotopes are associated with methane oxidation (especially in the upper stratosphere over the polar region), downward flux of water vapor from the mesosphere over the polar region, and its intrusion from the troposphere (especially over the tropics). With Odin/SMR data, we roughly found a linear relationship between δD and δ18O in the stratosphere above 25 km as,
δD = 1.6 × δ18O − 510
This linear association is different from that obtained in the troposphere or in the surface precipitation. We examined the δD-δ18O relationships in simulations of two SWING2 models with high model tops (reaching the stratopause), LMDZ4 and GISS. We found that the slope in the troposphere is 7.2 in both models, but it is 9.4 and 4.6 in LMDZ4 and GISS, respectively, in the stratosphere. Though there is uncertainty in the first retrieved H218O data, we still believe that the relationship between δD and δ18O in the stratosphere is not the same as in the surface precipitation or troposphere. This may be further explored in the future by assimilating satellite data or other sounding observations.
Regarding the simulation of SWIs, most models that contributed to SWING2 fail to simulate the stratospheric features of SWIs. The evidence we have from the model simulations strongly suggests that this failure is partly due to the lack of consideration of some key stratospheric processes (e.g., methane oxidation) in atmospheric models. There is still much room for upgrading the relevant chemical processes. Another significant feature of observed SWIs is the downward propagation of seasonal signal from the upper to the lower stratosphere over the polar regions, but this is almost entirely lacking in LMDZ4strato simulations, especially the dry anomaly. It might be related to some physical processes that affect the vertical exchange, and which need to be identified and improved.

6. Conclusions

To summarize, we have explored eight years of measurements obtained from Odin/SMR, by investigating the climatological features of stratospheric SWIs. The satellite dataset captures the expected characteristic features of stratospheric SWIs. Spatially, SWIs increase with altitude due to the methane oxidation occurring in the stratosphere. From a zonally-averaged sense, the three SWIs are quasi-symmetrical with respect to the equator, with more heavy water over high latitudes and less heavy water over the tropics, corresponding to the large-scale condensation that occurs in the tropical region. At high latitudes, large mixing ratios of SWIs are found in the upper stratosphere (35–50 km), and these tend to be transported from summer to winter hemisphere via the BDC. More H2O is produced over summer in the Northern Hemisphere and HDO is produced more over summer in the Southern Hemisphere.
For the seasonal cycle, Odin/SMR-retrieved H2O shows a tape recorder in the lower stratosphere, from 20 to 30 km over the tropics. Over the polar regions, there is a clear seasonal cycle signal at the stratopause in H2O, HDO, δD and H218O, but not δ18O, with a wet signal in summer and a dry signal in winter, in addition to a propagating signal downward to the middle and lower stratosphere.
Lastly, the comparison of stratospheric SWIs features from Odin/SMR measurement with those from the SWI-enabled model LMDZ4strato experiments has helped identify the contributions of key processes in the model. For example, implementing a methane oxidation parameterization and using an advection scheme that is not too diffusive, the LMDZ4strato model thus greatly improves the simulation of water isotope patterns in the stratosphere, but further research in this direction is warranted.

Acknowledgments

This work is supported by the Swedish National Space Board project Dnr 88/11 “Atmospheric modelling using space-based observations of stable water isotopes” and Swedish Research Council VR for the Swedish-French project “Greenland in a warming Arctic”. The authors would like to acknowledge Qiang Li for assistance in data preparation. We would like to thank four reviewers for their insightful comments that improved the manuscript. The LMDZ4 simulations were run on the Ada supercomputer at the IDRIS computing center under GENCI project 0292. The Odin/SMR data are available at http://odin.rss.chalmers.se, contact person Donal Murtagh ([email protected]).

Author Contributions

T. Wang and Q. Zhang conceived and designed the study; S. Lossow, L. Chafik and A. Hannachi contributed in the discussion of the results; The LMDZ4strto simulations were run by C. Risi; D. Murtagh provided Odin/SMR retrieved data. T. Wang and Q. Zhang wrote the paper; all co-authors contributed to revise the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Solomon, S.; Rosenlof, K.H.; Portmann, R.W.; Daniel, J.S.; Davis, S.M.; Sanford, T.J.; Plattner, J.K. Contributions of stratospheric water vapor to decadal changes in the rate of global warming. Science 2010, 327, 1219–1223. [Google Scholar] [CrossRef] [PubMed]
  2. Dessler, A.; Schoeberl, M.R.; Wang, T.; Davis, S.M.; Rosenlof, K.H. Stratospheric water vapor feedback. Proc. Natl. Acad. Sci. USA 2013, 110, 18087–18091. [Google Scholar] [CrossRef] [PubMed]
  3. Johnson, D.G.; Jucks, K.W.; Traub, W.A.; Chance, K.V. Isotopic composition of stratospheric water vapor: Implications for transport. J. Geophys. Res. 2001, 106, 12219–12226. [Google Scholar] [CrossRef]
  4. Bechtel, C.; Zahn, A. The isotope composition of water vapour: A powerful tool to study transport and chemistry of middle atmospheric water vapour. Atmos. Chem. Phys. Discuss. 2003, 3, 3991–4036. [Google Scholar] [CrossRef]
  5. Brewer, A.W. Evidence for a world circulation provided by the measurements of helium and water vapour distribution in the stratosphere. Q. J. R. Meteorol. Soc. 1949, 75, 351–363. [Google Scholar] [CrossRef]
  6. Dobson, G.M.B. Origin and distribution of the polyatomic molecules in the atmosphere. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1956, 236, 187–193. [Google Scholar] [CrossRef]
  7. Gettelman, A.; Kinnison, D.E.; Dunkerton, T.J.; Brasseur, G.P. Impact of monsoon circulations on the upper troposphere and lower stratosphere. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
  8. Khaykin, S.; Pommereau, J.P.; Korshunov, L.; Yushkov, V.; Nielsen, J.; Larsen, N.; Christensen, T.; Garnier, A.; Lukyanov, A.; Williams, E. Hydration of the lower stratosphere by ice crystal geysers over land convective systems. Atmos. Chem. Phys. 2009, 9, 2275–2287. [Google Scholar] [CrossRef] [Green Version]
  9. Zahn, A. Constraints on 2-way transport across the Arctic tropopause based on O3, stratospheric tracer (SF6) ages, and water vapor isotope (D, T) tracers. J. Atmos. Chem. 2001, 39, 303–325. [Google Scholar] [CrossRef]
  10. Texier, H.L.; Solomon, S.; Garcia, R.R. The role of molecular hydrogen and methane oxidation in the water vapour budget of the stratosphere. Q. J. R. Meteorol. Soc. 1988, 114, 281–295. [Google Scholar] [CrossRef]
  11. Ravishankara, A.R. Kinetics of radical reactions in the atmospheric oxidation of CH4. Annu. Rev. Phys. Chem. 1988, 39, 367–394. [Google Scholar] [CrossRef]
  12. Röckmann, T.; Rhee, T.S.; Engel, A. Heavy hydrogen in the stratosphere. Atmos. Chem. Phys. 2003, 3, 2015–2023. [Google Scholar] [CrossRef]
  13. Lyons, J.R. Transfer of mass-independent fractionation in ozone to other oxygen-containing radicals in the atmosphere. Geophys. Res. Lett. 2001, 28, 3231–3234. [Google Scholar] [CrossRef]
  14. Rinsland, C.P.; Gunson, M.R.; Foster, J.C.; Toth, R.A.; Farmer, C.B.; Zander, R. Stratospheric profiles of heavy water vapor isotopes and CH3D from analysis of the ATMOS Spacelab 3 infrared solar spectra. J. Geophys. Res. 1991, 96, 1057–1068. [Google Scholar] [CrossRef]
  15. Worden, J. Tropospheric Emission Spectrometer observations of the tropospheric HDO/H2O ratio: Estimation approach and characterization. J. Geophys. Res. 2006, 111, D16309. [Google Scholar] [CrossRef]
  16. Steinwagner, J.; Milz, M.; Clarmann, T.V.; Glatthor, N.; Grabowski, U.; Höpfner, M.; Stiller, G.; Röckmann, T. HDO measurements with MIPAS. Atmos. Chem. Phys. 2007, 7, 2601–2615. [Google Scholar] [CrossRef]
  17. Payne, V.H.; Noone, D.; Dudhia, A.; Piccolo, C.; Graingerb, R.G. Global satellite measurements of HDO and implications for understanding the transport of water vapour into the stratosphere. Q. J. R. Meteorol. Soc. 2007, 133, 1459–1471. [Google Scholar] [CrossRef]
  18. Steinwagner, J.; Fueglistaler, S.; Stiller, G.; Clarmann, T.V.; Kiefer, M.; Borsboom, P.P.; Delden, A.V.; Röckmann, T. Tropical dehydration processes constrained by the seasonality of stratospheric deuterated water. Nat. Geosci. 2010, 3, 262–266. [Google Scholar] [CrossRef]
  19. Randel, W.J.; Moyer, E.; Park, M.; Jensen, E.; Bernath, P.; Walker, K.; Boone, C. Global variations of HDO and HDO/H2O ratios in the upper troposphere and lower stratosphere derived from ACE-FTS satellite measurements. J. Geophys. Res. 2012, 117, D06303. [Google Scholar] [CrossRef]
  20. Zelinger, Z.; Barret, B.; Kubát, P.; Ricaud, P.; Attie, J.L.; Flochmoën, L.E.; Urban, J.; Murtagh, D.; Střižík, M. Observation of HD18O, CH3OH and vibrationally-excited N2O from Odin/SMR measurements. Mol. Phys. 2006, 104, 2815–2820. [Google Scholar] [CrossRef]
  21. Nassar, R.; Bernath, P.F.; Boone, C.D.; Gettelman, A.; McLeod, S.D.; Rinsland, C.P. Variability in HDO/H2O abundance ratios in the tropical tropopause layer. J. Geophys. Res. 2007, 112, D21305. [Google Scholar] [CrossRef]
  22. Schmidt, G.A.; Hoffmann, G.; Shindell, D.T.; Hu, Y. Modeling atmospheric stable water isotopes and the potential for constraining cloud processes and stratosphere—Troposphere water exchange. J. Geophys. Res. 2005, 110, D21314. [Google Scholar] [CrossRef]
  23. Noone, D. Evaluation of hydrological cycles and processes with water isotopes: Report to GEWEX-GHP from the Stable Water-isotope Intercomparison Group (SWING). In Proceedings of the Pan-GEWEX Meeting, Frascati, Italy, 9–13 October 2006. [Google Scholar]
  24. Risi, C.; Noone, D.; Worden, J.; Frankenberg, C.; Stiller, G.; Kiefer, M.; Funke, B.; Walker, K.; Bernath, P.; Schneider, M. Process-evaluation of tropospheric humidity simulated by general circulation models using water vapor isotopologues: 1. Comparison between models and observations. J. Geophys. Res. 2012, 117, D05303. [Google Scholar] [CrossRef]
  25. Risi, C.; Noone, D.; Worden, J.; Frankenberg, C.; Stiller, G.; Kiefer, M.; Funke, B.; Walker, K.; Bernath, P.; Schneider, M. Process-evaluation of tropospheric humidity simulated by general circulation models using water vapor isotopic observations: 2. Using isotopic diagnostics to understand the mid and upper tropospheric moist bias in the tropics and subtropics. J. Geophys. Res. Atmos. 2012, 117, 214–221. [Google Scholar] [CrossRef]
  26. Conroy, J.L.; Cobb, K.M.; Noone, D. Comparison of precipitation isotope variability across the tropical Pacific in observations and SWING2 model simulations. J. Geophys. Res. Atmos. 2013, 118, 5867–5892. [Google Scholar] [CrossRef]
  27. Hourdin, F.; Musat, I.; Bony, S.; Braconnot, P.; Codron, F.; Dufresne, J.L.; Fairhead, L.; Filiberti, M.A.; Friedlingstein, P.; Grandpeix, J.Y.; et al. The LMDZ general circulation model: Climate performance and sensitivity to parametrized physics with emphasis on tropical convection. Clim. Dyn. 2006, 27, 787–813. [Google Scholar] [CrossRef] [Green Version]
  28. Murtagh, D.; Frisk, U.; Merino, F.; Ridal, M.; Jonsson, A.; Stegman, J.; Witt, G.; Eriksson, P.; Jiménez, C.; Megie, G. An overview of the Odin atmospheric mission. Can. J. Phys. 2002, 80, 309–319. [Google Scholar] [CrossRef]
  29. Urban, J.; Lautié, N.; Murtagh, D.; Eriksson, P.; Kasai, Y.; Lossow, S.; Dupuy, E.; De La Noë, J.; Frisk, U.; Olberg, M.; et al. Global observations of middle atmospheric water vapour by the Odin satellite: An overview. Planet. Space Sci. 2007, 55, 1093–1102. [Google Scholar] [CrossRef]
  30. Urban, J.; Lautié, N.; Flochmoën, E.L.; Jiménez, C.; Eriksson, P.; Noë, J.L.; Dupuy, E.; Ekström, M.; Amraoui, L.E.; Frisk, U. Odin/SMR limb observations of stratospheric trace gases: Level 2 processing of ClO, N2O, HNO3, and O3. J. Geophys. Res. 2005, 110, D14307. [Google Scholar] [CrossRef]
  31. Jones, A.; Walker, K.A.; Jin, J.J.; Taylor, J.R.; Boone, C.D.; Bernath, P.F.; Brohede, S.; Manney, G.L.; McLeod, S.; Hughes, R.; et al. Technical Note: A trace gas climatology derived from the Atmospheric Chemistry Experiment Fourier Transform Spectrometer (ACE-FTS) data set. Atmos. Chem. Phys. 2012, 12, 5207–5220. [Google Scholar] [CrossRef] [Green Version]
  32. Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K. MERRA: NASA’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
  33. Coddington, O.; Lean, J.L.; Pilewskie, P.; Snow, M.; Lindholm, D. A solar irradiance climate data record. Bull. Am. Meteorol. Soc. 2015, 97, 1265–1282. [Google Scholar] [CrossRef]
  34. International Atomic Energy Agency (IAEA). Reference Sheet for VSMOW2 and SLAP2 International Measurement Standards; International Atomic Energy Agency: Vienna, Austria, 2009; p. 5. [Google Scholar]
  35. Lossow, S.; Steinwagner, J.; Urban, J.; Dupuy, E.; Boone, C.D.; Kellmann, S.; Linden, A.; Kiefer, M.; Grabowski, U.; Glatthor, N.; et al. Comparison of HDO measurements from Envisat/MIPAS with observations by Odin/SMR and SCISAT/ACE-FTS. Atmos. Meas. Tech. 2011, 4, 1855–1874. [Google Scholar] [CrossRef] [Green Version]
  36. Hurst, D.F.; Oltmans, S.J.; Vömel, H.; Rosenlof, K.H.; Davis, S.M.; Ray, E.A.; Hall, E.G.; Jordan, A.F. Stratospheric water vapor trends over Boulder, Colorado: Analysis of the 30 year Boulder record. J. Geophys. Res. 2011, 116, D02306. [Google Scholar] [CrossRef]
  37. Dessler, A.; Sherwood, S. A model of HDO in the tropical tropopause layer. Atmos. Chem. Phys. 2003, 3, 2173–2181. [Google Scholar] [CrossRef]
  38. Dessler, A.; Sherwood, S. Effect of convection on the summertime extratropical lower stratosphere. J. Geophys. Res. 2004, 109, D23301. [Google Scholar] [CrossRef]
  39. Moyer, E.J.; Irion, F.W.; Yung, Y.L.; Gunson, M.R. ATMOS stratospheric deuterated water and implications for troposphere-stratosphere transport. Geophys. Res. Lett. 1996, 23, 2385–2388. [Google Scholar] [CrossRef]
  40. Stiller, G.P.; Clarmann, T.V.; Haenel, F.; Funke, B.; Glatthor, N.; Grabowski, U.; Kellmann, S.; Kiefer, M.; Linden, A.; Lossow, S. Observed temporal evolution of global mean age of stratospheric air for the 2002 to 2010 period. Atmos. Chem. Phys. 2012, 12, 3311–3331. [Google Scholar] [CrossRef] [Green Version]
  41. Holton, J.R.; Haynes, P.H.; Mcintyre, M.E.; Douglass, A.R.; Rood, R.B.; Pfister, L. Stratosphere-troposphere exchange. Rev. Geophys. 1995, 33, 403–439. [Google Scholar] [CrossRef]
  42. Dunkerton, T. On the mean meridional mass motions of the stratosphere and mesosphere. J. Atmos. Sci. 1978, 35, 2325–2333. [Google Scholar] [CrossRef]
  43. Randel, W.J.; Wu, F.; Russell, J.M., III; Roche, A.; Waters, J.W. Seasonal cycles and QBO variations in stratospheric CH4 and H2O observed in UARS HALOE data. J. Atmos. Sci. 1998, 55, 163–185. [Google Scholar] [CrossRef]
  44. Mote, P.W.; Rosenlof, K.H.; McIntyre, M.E.; Carr, E.S.; Gille, J.C.; Holton, J.R.; Kinnersley, J.S.; Pumphrey, H.C.; Russell, J.M.; Waters, J.W. An atmospheric tape recorder: The imprint of tropical tropopause temperatures on stratospheric water vapor. J. Geophys. Res. 1996, 101, 3989–4006. [Google Scholar] [CrossRef]
  45. Eichinger, R.; Jöckel, P.; Brinkop, S.; Werner, M.; Lossow, S. Simulation of the isotopic composition of stratospheric water vapour–Part 1: Description and evaluation of the EMAC model. Atmos. Chem. Phys. 2015, 15, 5537–5555. [Google Scholar] [CrossRef] [Green Version]
  46. Sturm, C.; Zhang, Q.; Noone, D. An introduction to stable water isotopes in climate models: Benefits of forward proxy modelling for paleoclimatology. Clim. Past 2010, 6, 115–129. [Google Scholar] [CrossRef]
  47. Risi, C.; Bony, S.; Vimeux, F.; Jouzel, J. Water-stable isotopes in the LMDZ4 general circulation model: Model evaluation for present-day and past climates and applications to climatic interpretations of tropical isotopic records. J. Geophys. Res. 2010, 115, D12118. [Google Scholar] [CrossRef]
  48. Marti, O.; Braconnot, P.; Bellier, J.; Benshile, R.; Bony, S.; Brockmann, P.; Cadulle, P.; Caubel, A.; Denvil, S.; Dufresne, J.L.; et al. The New IPSL Climate System Model: IPSL-CM4; Institut Pierre Simon Laplace: Paris, France, 2005; 86p. [Google Scholar]
  49. Emanuel, K.A.; Živković-Rothman, M. Development and evaluation of a convection scheme for use in climate models. J. Atmos. Sci. 1999, 56, 1766–1782. [Google Scholar] [CrossRef]
  50. Bony, S.; Emanuel, K.A. A parameterization of the cloudiness associated with cumulus convection; evaluation using TOGA COARE data. J. Atmos. Sci. 2001, 58, 3158–3183. [Google Scholar] [CrossRef]
  51. Klinker, E.; Rabier, F.; Kelly, G.; Mahfouf, J.F. The ecmwf operational implementation of four-dimensional variational assimilation. III: Experimental results and diagnostics with operational configuration. Q. J. R. Meteorol. Soc. 2000, 126, 1191–1215. [Google Scholar] [CrossRef]
  52. Van, L.B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar]
  53. Brasseur, G.; Solomon, S. Aeronomy of the Middle Atmosphere; D. Reidel Publishing Co.: Dordrecht, The Netherlands, 1984. [Google Scholar]
  54. Lott, F.; Fairhead, L.; Hourdin, F.; Levan, P. The stratospheric version of LMDz: Dynamical Climatologies, Arctic Oscillation, and Impact on the Surface Climate. Clim. Dyn. 2005, 25, 851–868. [Google Scholar] [CrossRef]
  55. Schmidt, G.; LeGrande, A.; Hoffmann, G. Water isotope expressions of intrinsic and forced variability in a coupled ocean-atmosphere model. J. Geophys. Res. 2007, 112, D10103. [Google Scholar] [CrossRef]
  56. Yoshimura, K.; Kanamitsu, M.; Noone, D.; Oki, T. Historical isotope simulation using Reanalysis atmospheric data. J. Geophys. Res. 2008, 113, D19108. [Google Scholar] [CrossRef]
  57. Kurita, K.; Noone, D.; Risi, C.; Schmidt, G.A.; Yamada, H.; Yoneyama, K. Intraseasonal isotopic variation associated with the Madden-Julian Oscillation. J. Geophys. Res. 2011, 116, D24101. [Google Scholar] [CrossRef]
  58. Gates, W.L. AMIP: The atmospheric model intercomparison project. Bull. Am. Meteorol. Soc. 1992, 73, 1962–1970. [Google Scholar] [CrossRef]
  59. Godunov, S.K. A difference method for numerical calculation of discontinuous solutions of the equations of hydrodynamics. Mat. Sb. 1959, 89, 271–306. [Google Scholar]
  60. Craig, H. Isotopic variations in meteoric waters. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef] [PubMed]
  61. Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, 16, 436–468. [Google Scholar] [CrossRef]
Remotesensing 10 00166 g001 550
Figure 1. Global sampling of the Odin/SMR (Sub-Millimetre Radiometer) observations in January 2003.
Figure 1. Global sampling of the Odin/SMR (Sub-Millimetre Radiometer) observations in January 2003.
Remotesensing 10 00166 g001
Remotesensing 10 00166 g002 550
Figure 2. Climatological vertical profiles of global averaged: (a) H2O (black solid) and air temperature (red dashed); (b) δD (blue) and δ18O (purple); (c) standard deviation of H2O; and (d) standard deviations of δD (blue) and δ18O (purple).
Figure 2. Climatological vertical profiles of global averaged: (a) H2O (black solid) and air temperature (red dashed); (b) δD (blue) and δ18O (purple); (c) standard deviation of H2O; and (d) standard deviations of δD (blue) and δ18O (purple).
Remotesensing 10 00166 g002
Remotesensing 10 00166 g003 550
Figure 3. Zonal mean of climatological averaged: H2O (unit: ppmv) (a); δD (unit: ‰) (c); and δ18O (unit: ‰) (e); and their standard deviation for annual mean (b,d,f). The blue, black and red lines represent the value of 20–30 km, 30–40 km, and 40–50 km vertical mean, respectively, in each panel. The climatology is based on the 2002–2009 period.
Figure 3. Zonal mean of climatological averaged: H2O (unit: ppmv) (a); δD (unit: ‰) (c); and δ18O (unit: ‰) (e); and their standard deviation for annual mean (b,d,f). The blue, black and red lines represent the value of 20–30 km, 30–40 km, and 40–50 km vertical mean, respectively, in each panel. The climatology is based on the 2002–2009 period.
Remotesensing 10 00166 g003
Remotesensing 10 00166 g004 550
Figure 4. Latitude–altitude sections of: H2O (shaded in (a,b)); HD16O (hereafter HDO) (c,d); H218O (e,f); and air temperature (contour in (a,b), unit: K). The left column shows the DJF mean; right column shows the JJA mean. The climatology is based on the 2002–2009 period.
Figure 4. Latitude–altitude sections of: H2O (shaded in (a,b)); HD16O (hereafter HDO) (c,d); H218O (e,f); and air temperature (contour in (a,b), unit: K). The left column shows the DJF mean; right column shows the JJA mean. The climatology is based on the 2002–2009 period.
Remotesensing 10 00166 g004
Remotesensing 10 00166 g005 550
Figure 5. Latitude–altitude sections of δD (a,b); and δ18O (c,d). The left column shows the DJF mean; right column shows the JJA mean. The climatology is based on the 2002–2009 period.
Figure 5. Latitude–altitude sections of δD (a,b); and δ18O (c,d). The left column shows the DJF mean; right column shows the JJA mean. The climatology is based on the 2002–2009 period.
Remotesensing 10 00166 g005
Remotesensing 10 00166 g006 550
Figure 6. Scatter diagram of mean H218O of summer hemisphere in the upper stratosphere (45–55 km), versus the total solar irradiance. Blue and red dots represent the Southern and Northern Hemisphere, respectively.
Figure 6. Scatter diagram of mean H218O of summer hemisphere in the upper stratosphere (45–55 km), versus the total solar irradiance. Blue and red dots represent the Southern and Northern Hemisphere, respectively.
Remotesensing 10 00166 g006
Remotesensing 10 00166 g007 550
Figure 7. Seasonal cycle of the vertical structure over the tropics (15°S–15°N mean) for anomaly of H2O. Note that the indicated years on the x-axis are centered at July.
Figure 7. Seasonal cycle of the vertical structure over the tropics (15°S–15°N mean) for anomaly of H2O. Note that the indicated years on the x-axis are centered at July.
Remotesensing 10 00166 g007
Remotesensing 10 00166 g008 550
Figure 8. Seasonal cycle of vertical structures over south polar region (60°S–85°S mean) for the anomalies of: H2O (a); HDO (b); H218O (c); and δD (d).
Figure 8. Seasonal cycle of vertical structures over south polar region (60°S–85°S mean) for the anomalies of: H2O (a); HDO (b); H218O (c); and δD (d).
Remotesensing 10 00166 g008
Remotesensing 10 00166 g009 550
Figure 9. Latitude–altitude sections of DJF (left column) and JJA (right column) mean: H2O (a,b); δD (c,d); and δ18O (e,f), simulated by the LMDZ4strato Exp1. The climatology is based on the 2002–2009 period.
Figure 9. Latitude–altitude sections of DJF (left column) and JJA (right column) mean: H2O (a,b); δD (c,d); and δ18O (e,f), simulated by the LMDZ4strato Exp1. The climatology is based on the 2002–2009 period.
Remotesensing 10 00166 g009
Remotesensing 10 00166 g010 550
Figure 10. Seasonal cycle of vertical structures for H2O anomaly: (a) over the tropics (15°S–15°N mean); and (b) over the south polar region (60°S–85°S mean), simulated by the model LMDZ4strato Exp1. Note that the indicated years on the x-axis are centered at July.
Figure 10. Seasonal cycle of vertical structures for H2O anomaly: (a) over the tropics (15°S–15°N mean); and (b) over the south polar region (60°S–85°S mean), simulated by the model LMDZ4strato Exp1. Note that the indicated years on the x-axis are centered at July.
Remotesensing 10 00166 g010
Remotesensing 10 00166 g011 550
Figure 11. Latitude–altitude sections of DJF (left column) and JJA (right column) mean H2O (shaded and contour, unit: ppmv) simulated by SWING2 models. The model climatology is based on the 2002–2009 period.
Figure 11. Latitude–altitude sections of DJF (left column) and JJA (right column) mean H2O (shaded and contour, unit: ppmv) simulated by SWING2 models. The model climatology is based on the 2002–2009 period.
Remotesensing 10 00166 g011
Remotesensing 10 00166 g012 550
Figure 12. Latitude–pressure profile of DJF (left column) and JJA (right column) mean H2O (shaded and contour, unit: ppmv) simulated by LMDZ4strato: Exp2 (a,b); and Exp3 (c,d). The climatology is based on the 2002–2009 period.
Figure 12. Latitude–pressure profile of DJF (left column) and JJA (right column) mean H2O (shaded and contour, unit: ppmv) simulated by LMDZ4strato: Exp2 (a,b); and Exp3 (c,d). The climatology is based on the 2002–2009 period.
Remotesensing 10 00166 g012

Share and Cite

MDPI and ACS Style

Wang, T.; Zhang, Q.; Lossow, S.; Chafik, L.; Risi, C.; Murtagh, D.; Hannachi, A. Stable Water Isotopologues in the Stratosphere Retrieved from Odin/SMR Measurements. Remote Sens. 2018, 10, 166. https://doi.org/10.3390/rs10020166

AMA Style

Wang T, Zhang Q, Lossow S, Chafik L, Risi C, Murtagh D, Hannachi A. Stable Water Isotopologues in the Stratosphere Retrieved from Odin/SMR Measurements. Remote Sensing. 2018; 10(2):166. https://doi.org/10.3390/rs10020166

Chicago/Turabian Style

Wang, Tongmei, Qiong Zhang, Stefan Lossow, Léon Chafik, Camille Risi, Donal Murtagh, and Abdel Hannachi. 2018. "Stable Water Isotopologues in the Stratosphere Retrieved from Odin/SMR Measurements" Remote Sensing 10, no. 2: 166. https://doi.org/10.3390/rs10020166

APA Style

Wang, T., Zhang, Q., Lossow, S., Chafik, L., Risi, C., Murtagh, D., & Hannachi, A. (2018). Stable Water Isotopologues in the Stratosphere Retrieved from Odin/SMR Measurements. Remote Sensing, 10(2), 166. https://doi.org/10.3390/rs10020166

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop