Sensitivity and Limitation in Damage Detection for Individual Buildings Using InSAR Coherence—A Case Study in 2016 Kumamoto Earthquakes
Abstract
:1. Introduction
2. Methodology
2.1. Multi-Temporal Interferometric Coherence
2.2. Aerial Photography Survey
- To fix unstable parts to keep residents’ safe when walking around the building.
- For thermal insulation to stop any air drafts from the damaged roof.
- To avoid further damage by leaks caused by rain.
2.3. Inventory Survey Results in Sampled Region of Mashikimachi Town
- Threshold of the coherence decrease (CD) dγun.
- The smallest size of the building to judge.
- Ratio of the CD region per building .
3. 2016 Kumamoto, Japan Earthquakes and ALOS-2 Observations
4. Experimental Results
4.1. Aerial Photography Survey in a Larger Scale
4.2. Inventory Survey in a Smaller Scale
- The size of the building is 200 m2 or larger.
- The damage level of the building is DL 2 or higher.
- If a building is too small, smaller than 200 m2 in this case, it is not possible to assess the DL with coherence analysis.
- There were two thresholds. One is to detect DL 2 (moderate damaged) or higher (DL 3–5) buildings and, the other one is to detect DL 5 (totally collapsed) buildings. However, there was no appropriate threshold that can distinguish DL 3–5 or DL 4–5 from the others.
- The threshold of the coherence has a proportional relationship with the ratio between CD region and the size of the building. Most damaged buildings present a little decrease of the coherence in the large part of the building, or a large decrease of the coherence in the small part of the building.
5. Discussion
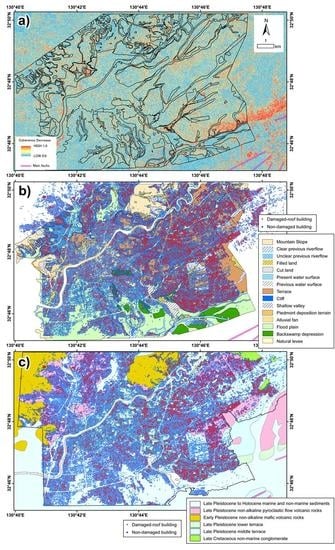
5.1. Distribution of Damaged Buildings
5.2. Ambiguity of Coherence Threshold
5.3. Minimum Size of the Buildingc
5.4. Origin of Low Coherency
- Temporal decorrelation
- Baseline decorrelation
- Ionospheric and tropospheric decorrelations
- Decorrelation in phase discontinuities
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Plank, S. Rapid damage assessment by means of multi-temporal SAR—A comprehensive review and outlook to Sentinel-1. Remote Sens. 2014, 6, 4870–4906. [Google Scholar] [CrossRef] [Green Version]
- Milillo, P.; Riel, B.; Minchew, B.; Yun, S.H.; Simons, M.; Lundgren, P. On the synergistic use of SAR constellations’ data exploitation for earth science and natural hazard response. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 1095–1100. [Google Scholar] [CrossRef]
- Stramondo, S.; Bignami, C.; Chini, M.; Pierdicca, N.; Tertulliani, A. Satellite radar and optical remote sensing for earthquake damage detection: Results from different case studies. Int. J. Remote Sens. 2006, 27, 4433–4447. [Google Scholar] [CrossRef]
- Brunner, D.; Lemoine, G.; Bruzzone, L. Earthquake damage assessment of buildings using VHR optical and SAR imagery. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2403–2420. [Google Scholar] [CrossRef]
- Matsuoka, M.; Yamazaki, F. Building damage mapping of the 2003 Bam, Iran, earthquake using ENVISAT/ASAR intensity imagery. Earthq. Spectra 2005, 21, S285–S294. [Google Scholar] [CrossRef]
- Fielding, E.J. Surface ruptures and building damage of the 2003 Bam, Iran, earthquake mapped by satellite synthetic aperture radar interferometric correlation. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Arciniegas, G.A.; Bijker, W.; Kerle, N.; Tolpekin, V.A. Coherence- and amplitude-based analysis of seismogenic damage in bam, Iran, using ENVISAT ASAR data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1571–1581. [Google Scholar] [CrossRef]
- Yamaguchi, Y. Disaster monitoring by fully polarimetric SAR data acquired with ALOS-PALSAR. Proc. IEEE 2012, 100, 2851–2860. [Google Scholar] [CrossRef]
- Sato, M.; Chen, S.W.; Satake, M. Polarimetric SAR analysis of tsunami damage following the March 11, 2011 East Japan Earthquake. Proc. IEEE 2012, 100, 2861–2875. [Google Scholar] [CrossRef]
- Watanabe, M.; Motohka, T.; Miyagi, Y.; Yonezawa, C.; Shimada, M. Analysis of urban areas affected by the 2011 off the pacific coast of Tohoku Earthquake and Tsunami with L-band SAR full-polarimetric mode. IEEE Geosci. Remote Sens. Lett. 2012, 9, 472–476. [Google Scholar] [CrossRef]
- Chen, S.W.; Sato, M. Tsunami damage investigation of built-up areas using multitemporal spaceborne full polarimetric SAR images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1985–1997. [Google Scholar] [CrossRef]
- Chen, S.W.; Wang, X.S.; Sato, M. Urban damage level mapping based on scattering mechanism investigation using fully polarimetric SAR data for the 3.11 East Japan earthquake. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6919–6929. [Google Scholar] [CrossRef]
- Nakmuenwai, P.; Yamazaki, F.; Liu, W. Multi-temporal correlation method for damage assessment of buildings from high-resolution SAR images of the 2013 typhoon Haiyan. J. Disaster Res. 2016, 11, 577–592. [Google Scholar] [CrossRef]
- Bouaraba, A.; Younsi, A.; Belhadj-Aissa, A.; Acheroy, M.; Milisavljevic, N.; Closson, D. Robust techniques for coherent change detection using COSMO-SkyMed SAR images. Prog. Electromagn. Res. M 2012, 22, 219–232. [Google Scholar] [CrossRef]
- Chini, M.; Albano, M.; Saroli, M.; Pulvirenti, L.; Moro, M.; Bignami, C.; Falcucci, E.; Gori, S.; Modoni, G.; Pierdicca, N.; et al. Coseismic liquefaction phenomenon analysis by COSMO-SkyMed: 2012 Emilia (Italy) earthquake. Int. J. Appl. Earth Observ. Geoinf. 2015, 39, 65–78. [Google Scholar] [CrossRef]
- Wei, M.; Sandwell, D.T. Decorrelation of L-band and C-band interferometry over vegetated areas in California. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2942–2952. [Google Scholar]
- Yonezawa, C.; Takeuchi, S. Decorrelation of SAR data by urban damages caused by the 1995 Hyogokennanbu earthquake. Int. J. Remote Sens. 2011, 22, 1585–1600. [Google Scholar] [CrossRef]
- Matsuoka, M.; Nojima, N. Building damage estimation by integration of seismic intensity information and satellite L-band SAR imagery. Remote Sens. 2010, 2, 2111–2126. [Google Scholar] [CrossRef]
- Gokon, H.; Koshimura, S.; Meguro, K. Verification of a method for estimating building damage in extensive tsunami affected areas using L-band SAR data. J. Disaster Res. 2017, 12, 251–258. [Google Scholar] [CrossRef]
- Arikawa, Y.; Saruwatari, H.; Hatooka, Y.; Suzuki, S. PALSAR-2 launch and early orbit operation result. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 3406–3409. [Google Scholar]
- Bai, Y.; Adriano, B.; Mas, E.; Gokon, H.; Koshimura, S. Object-based building damage assessment methodology using only post event ALOS-2/PALSAR-2 dual polarimetric SAR intensity images. J. Disaster Res. 2017, 12, 259–271. [Google Scholar] [CrossRef]
- Watanabe, M.; Thapa, R.B.; Ohsumi, T.; Fujiwara, H.; Yonezawa, C.; Tomii, N.; Suzuki, S. Detection of damaged urban areas using interferometric SAR coherence change with PALSAR-2. Earth Planets Space 2016, 68. [Google Scholar] [CrossRef]
- Dell Acqua, F.; Gamba, P. Remote sensing and earthquake damage assessment: Experiences, limits, and perspectives. Proc. IEEE 2012, 100, 2876–2890. [Google Scholar] [CrossRef]
- Grunthal, G. (Ed.) European Macroseismic Scale 1998; Centre Europeen de Geodynamique et de Seismologie: Luxembourg, 1998. [Google Scholar]
- Liu, W.; Yamazaki, F. Extraction of collapsed buildings in the 2016 Kumamoto earthquake using multitemporal PALSAR-2 data. J. Disaster Res. 2017, 12, 241–250. [Google Scholar] [CrossRef]
- Natsuaki, R.; Anahara, T.; Kotoura, T.; Iwatsuka, Y.; Tomii, N.; Katayama, H.; Nishihata, T. Synthetic aperture radar interferometry for disaster monitoring of harbor facilities. J. Disaster Res. 2017, 12, 526–535. [Google Scholar] [CrossRef]
- Yoshida, K.; Hasegawa, A.; Saito, T.; Asano, Y.; Tanaka, S.; Sawazaki, K.; Urata, Y.; Fukuyama, E. Stress rotations due to the M 6.5 foreshock and M 7.3 main shock in the 2016 Kumamoto, SW Japan, earthquake sequence. Geophys. Res. Lett. 2016, 43, 10097–10104. [Google Scholar] [CrossRef]
- Uchide, T.; Horikawa, H.; Nakai, M.; Matsushita, R.; Shigematsu, N.; Ando, R.; Imanishi, K. The 2016 Kumamoto–Oita earthquake sequence: Aftershock seismicity gap and dynamic triggering in volcanic areas. Earth Planets Space 2016, 68. [Google Scholar] [CrossRef]
- Google, New 3D Imagery for Google Earth. Available online: https://www.youtube.com/watch?v=N6Douyfa7l8 (accessed on 17 April 2017).
- Geospatial Information Authority (GSI) of Japan, Vector-Format Feature Data. Available online: http://www.gsi.go.jp/kiban/ (accessed on 17 April 2017). (In Japanese)
- Geological Survey of Japan, AIST (Ed.) Seamless digital geological map of Japan 1: 200000. 8 December 2017 version. Geological Survey of Japan, National Institute of Advanced Industrial Science and Technology. 2017. Available online: https://gbank.gsj.jp/seamless/index_en.html (accessed on 13 January 2017).
- Geospatial Information Authority (GSI) of Japan, Geomorphic Classification Map for Flood Control. Available online: http://www.gsi.go.jp/bousaichiri/fc list a.html (accessed on 17 April 2017). (In Japanese).
- Saeki, T. Building damage survey of 2016 Kumamoto earthquake. In Proceedings of the Sixth Workshop of Japan-New Zealand-Taiwan Seismic Hazard Assessment 2016, Beppu, Japan, 31 October–4 November 2016. [Google Scholar]
- Okada, S.; Takai, N. Classifications of structural types and damage patterns of buildings for earthquake field investigation. J. Struct. Constr. Eng.-AIJ 1999, 524, 65–72. (In Japanese) [Google Scholar] [CrossRef]
- Takai, N.; Okada, S. Classifications of damage patterns of reinforced concrete buildings for earthquake field investigation. J. Struct. Constr. Eng.-AIJ 2001, 549, 67–74. (In Japanese) [Google Scholar] [CrossRef]
- Natsuaki, R.; Hirose, A. InSAR local co-registration method assisted by shape-from-shading. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2013, 6, 953–959. [Google Scholar] [CrossRef]
- Yun, S.; Fielding, E.; Webb, F.; Simons, M. Damage Proxy Map from InSAR Coherence. U.S. Patent Application Serial Number: 13/528,610, 22 June 2012. [Google Scholar]
- Yun, S.H.; Hudnut, K.; Owen, S.; Webb, F.; Simons, M.; Sacco, P.; Gurrola, E.; Manipon, G.; Liang, C.; Fielding, E.; et al. Rapid Damage Mapping for the 2015 Mw 7.8 Gorkha Earthquake Using Synthetic Aperture Radar Data from COSMO–SkyMed and ALOS-2 Satellites. Seismol. Res. Lett. 2015, 86, 1549–1556. [Google Scholar] [CrossRef]
- Touzi, R.; Lopes, A.; Bruniquel, J.; Vachon, P.W. Coherence estimation for SAR imagery. IEEE Trans. Geosci. Remote Sens. 1999, 37, 135–149. [Google Scholar] [CrossRef]
- Lopez-Martinez, C.; Pottier, E. Coherence estimation in synthetic aperture radar data based on speckle noise modeling. Appl. Opt. 2007, 46, 544–558. [Google Scholar] [CrossRef] [PubMed]
- Fujiwara, S.; Yarai, H.; Kobayashi, T.; Morishita, Y.; Nakano, T.; Miyahara, B.; Nakai, H.; Miura, Y.; Ueshiba, H.; Kakiage, Y.; et al. Small-displacement linear surface ruptures of the 2016 Kumamoto earthquake sequence detected by ALOS-2 SAR interferometry. Earth Planets Space 2016, 68. [Google Scholar] [CrossRef]
- Zebker, H.A.; Chen, K. Accurate estimation of correlation in InSAR observations. IEEE Geosci. Remote Sens. Lett. 2005, 2, 124–127. [Google Scholar] [CrossRef]









| DL | 0 | 1 | 2 | 3 | 4 | 5 | Total | |
|---|---|---|---|---|---|---|---|---|
| Size[m2] | ||||||||
| 0–49 | 2 | 1 | 3 | 1 | 1 | 2 | 10 | |
| 50–99 | 10 | 14 | 4 | 8 | 12 | 2 | 50 | |
| 100–149 | 10 | 7 | 11 | 15 | 11 | 6 | 60 | |
| 150–199 | 2 | 6 | 2 | 7 | 6 | 4 | 27 | |
| 200–249 | 0 | 3 | 1 | 0 | 2 | 2 | 8 | |
| ≥250 | 9 | 6 | 5 | 2 | 6 | 2 | 30 | |
| Total | 33 | 37 | 26 | 33 | 38 | 18 | ||
| Geomorphic Type | Whole Building | Damaged Roof Building | ||
|---|---|---|---|---|
| Count | (%) | Count | (%) | |
| Mountain Slope | 4621 | 2.8 | 437 | 9.5 |
| Terrace | 66,384 | 40.2 | 8645 | 13.0 |
| Cliff | 1690 | 1.0 | 146 | 8.6 |
| Shallow valley | 4182 | 2.5 | 572 | 13.7 |
| Piedmont deposition terrain | 1869 | 1.1 | 150 | 8.0 |
| Alluvial fan | 24,389 | 14.8 | 1343 | 5.4 |
| Floo plain | 24,796 | 15.0 | 1312 | 5.3 |
| Backswamp & depression | 1779 | 1.1 | 96 | 5.4 |
| Natural levee | 13,223 | 8.0 | 888 | 6.7 |
| Clear previous riverflow | 513 | 0.3 | 19 | 3.7 |
| Unclear previous riverflow | 2348 | 1.4 | 146 | 6.2 |
| Filled land | 1614 | 1.0 | 48 | 3.0 |
| Cut land | 2297 | 1.4 | 128 | 5.6 |
| Out of map | 15,472 | 9.4 | 1738 | 11.2 |
| Sum | 165,177 | 15,668 | ||
| Overall Acc. | Ratio of CD Region per Building | |||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| Coherence threshold | 0.2 | 0.53 | 0.55 | 0.58 | 0.63 | 0.71 | 0.74 | 0.76 | 0.76 | 0.68 |
| 0.3 | 0.55 | 0.63 | 0.71 | 0.79 | 0.68 | 0.82 | 0.74 | 0.63 | 0.58 | |
| 0.4 | 0.68 | 0.79 | 0.79 | 0.79 | 0.71 | 0.71 | 0.63 | 0.55 | 0.47 | |
| 0.5 | 0.82 | 0.84 | 0.68 | 0.63 | 0.66 | 0.55 | 0.50 | 0.47 | 0.47 | |
| 0.6 | 0.79 | 0.74 | 0.63 | 0.55 | 0.53 | 0.47 | 0.47 | 0.47 | 0.47 | |
| K. Coeff. | Ratio of CD Region per Building | |||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| Coherence threshold | 0.2 | 0.00 | 0.06 | 0.12 | 0.23 | 0.40 | 0.46 | 0.52 | 0.53 | 0.38 |
| 0.3 | 0.06 | 0.23 | 0.40 | 0.57 | 0.36 | 0.63 | 0.48 | 0.28 | 0.19 | |
| 0.4 | 0.34 | 0.57 | 0.57 | 0.58 | 0.43 | 0.44 | 0.29 | 0.14 | 0.00 | |
| 0.5 | 0.63 | 0.68 | 0.38 | 0.28 | 0.34 | 0.14 | 0.05 | 0.00 | 0.00 | |
| 0.6 | 0.58 | 0.49 | 0.29 | 0.14 | 0.10 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Overall Acc. | Ratio of CD Region per Building | |||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| Coherence threshold | 0.2 | 0.11 | 0.13 | 0.16 | 0.21 | 0.29 | 0.32 | 0.34 | 0.66 | 0.74 |
| 0.3 | 0.13 | 0.21 | 0.29 | 0.37 | 0.42 | 0.55 | 0.74 | 0.84 | 0.89 | |
| 0.4 | 0.26 | 0.37 | 0.47 | 0.58 | 0.71 | 0.82 | 0.84 | 0.92 | 0.89 | |
| 0.5 | 0.45 | 0.58 | 0.68 | 0.84 | 0.87 | 0.92 | 0.92 | 0.89 | 0.89 | |
| 0.6 | 0.68 | 0.79 | 0.89 | 0.92 | 0.95 | 0.89 | 0.89 | 0.89 | 0.89 | |
| K Coeff. | Ratio of CD Region per Building | |||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | ||
| Coherence threshold | 0.2 | 0.00 | 0.01 | 0.01 | 0.03 | 0.05 | 0.00 | 0.01 | 0.18 | 0.16 |
| 0.3 | 0.01 | 0.03 | 0.05 | 0.08 | 0.04 | 0.11 | 0.26 | 0.42 | 0.44 | |
| 0.4 | 0.04 | 0.08 | 0.13 | 0.12 | 0.23 | 0.37 | 0.31 | 0.53 | 0.00 | |
| 0.5 | 0.12 | 0.19 | 0.20 | 0.42 | 0.48 | 0.53 | 0.37 | 0.00 | 0.00 | |
| 0.6 | 0.28 | 0.33 | 0.54 | 0.53 | 0.64 | 0.00 | 0.00 | 0.00 | 0.00 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Natsuaki, R.; Nagai, H.; Tomii, N.; Tadono, T. Sensitivity and Limitation in Damage Detection for Individual Buildings Using InSAR Coherence—A Case Study in 2016 Kumamoto Earthquakes. Remote Sens. 2018, 10, 245. https://doi.org/10.3390/rs10020245
Natsuaki R, Nagai H, Tomii N, Tadono T. Sensitivity and Limitation in Damage Detection for Individual Buildings Using InSAR Coherence—A Case Study in 2016 Kumamoto Earthquakes. Remote Sensing. 2018; 10(2):245. https://doi.org/10.3390/rs10020245
Chicago/Turabian StyleNatsuaki, Ryo, Hiroto Nagai, Naoya Tomii, and Takeo Tadono. 2018. "Sensitivity and Limitation in Damage Detection for Individual Buildings Using InSAR Coherence—A Case Study in 2016 Kumamoto Earthquakes" Remote Sensing 10, no. 2: 245. https://doi.org/10.3390/rs10020245
APA StyleNatsuaki, R., Nagai, H., Tomii, N., & Tadono, T. (2018). Sensitivity and Limitation in Damage Detection for Individual Buildings Using InSAR Coherence—A Case Study in 2016 Kumamoto Earthquakes. Remote Sensing, 10(2), 245. https://doi.org/10.3390/rs10020245